基于机器学习的学生学情预警方法研究

曹梦川　欧阳仪　伍丹　杜朋轩

摘  要：对学生的学习成绩进行预测分析，提前预警学生可能存在的挂科或成绩下降风险，从而帮助学生和教师更好地制定学习计划和提高教学效率。采集了包括学生的平时成绩、考勤、性别和期末成绩等多种因素的数据，使用线性回归模型进行数据建模和预测分析。研究结果表明，该模型预测误差小，具有实际应用价值。研究成果可为学生和教师提供有益的参考，以便更好地实现教育教学目标。

关键词：机器学习；数据建模；预测分析；线性回归

中图分类号：TP181；TP39  文献标识码：A  文章编号：2096-4706（2023）19-0142-04

Research on Student Learning Situation Early Warning Method Based on Machine Learning

CAO Mengchuan， OU Yangyi， WU Dan， DU Pengxuan

（Ningxia Polytechnic， Ningxia  750021， China）

Abstract： This research focuses on predicting and analyzing students' academic performance， gives an early warning of possible risk of failing or declining grades in advance， and helps students and teachers better plan their studies and improve teaching efficiency. The research collects data on various factors including students' regular grades， attendance， gender， and final grades， and uses linear regression models for data modeling and prediction analysis. The results show that the model has small prediction errors and practical application value. The results of this research can provide useful references for students and teachers to better achieve educational and teaching goals.

Keywords： Machine Learning; data modeling; prediction analysis; linear regression

0  引  言

學生成绩是评价学生学习成果的重要指标之一。然而，现今本科、大专的教育模式与高中、初中的截然不同，因每学期代课的班级、院系、年级不同，教师很难及时关注所有学生的学习情况。当学生在学习过程中出现学习状态下滑、成绩掉落、有期末挂科风险等情况，教师无法及时帮助学生调整学习状态，学生也会因此产生消极的学习态度。因此，如何对学生学习情况进行监控预警，及时发现学生在学习过程中的问题并提供对应的帮助，是教育工作者和家长们一直关注的问题。在这样的背景下，本文提出了一种使用机器学习对学生平时成绩进行数据建模以预警学生学习情况的方法。

1  实现方法

本次研究采用Python为主要开发语言，Python拥有众多可用于数据科学、人工智能、机器学习等领域的开发库，可以帮助开发者更加高效地编写和构建程序，大幅简化代码编写，将重心更多地放在科研中。开发工具采用Jupyter Notebook；使用Pandas开发库进行数据前期数据清洗、特征处理；采用的机器学习算法、二值化、特征缩放、模型构建、模型评分、数据集划分等方法来自scikit-learn开发库。

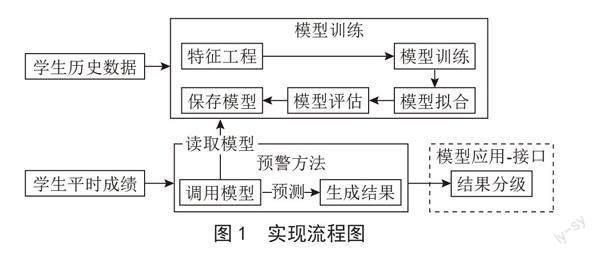
1.1  流程设计

图1为学生平时成绩预测模型的实现流程图。

1.2  原始数据集建立

本文以宁夏职业技术学院软件学院2021级100位学生在2021—2022年第二学期所学“数据分析与应用”课程的历史数据作为原始数据，采集特征包括学生的姓名、学号、性别、年级、期中成绩、平时成绩、考勤、期末成绩、课堂作业成绩。

1.3  特征工程

特征工程是对学生学情预警数据建模的第二步，也是最重要的一步，它是指对原始数据进行特征提取、特征转换和特征选择等操作，以获得对建模有用的特征（图2）。特征工程是建立学生学习成绩模型的关键环节，直接影响模型的准确性和实用性。将经过特征工程处理后的数据集划分为训练集和测试集，其中训练集占80%，测试集占20%，便于后续的测试与验证。

1.3.1  数据清洗

数据清洗是指在对原始数据进行处理之前，对数据进行检查、修改和删除，以确保数据质量和准确性的过程。在本次研究中，首先要检查学生信息是否存在缺失值和异常值，如果存在缺失值，需要采用合适的方式对数据进行处理，例如当该学生的成绩出现了空缺值，可采用该名学生的平均值填充；如果存在异常值，则删除该数据。

1.3.2  特征提取

特征提取是机器学习中的一个重要步骤，其目的是将原始数据转换为更具有代表性的特征。在机器学习中，特征是指用于描述数据的属性或特性。良好的特征提取可以帮助机器学习算法更准确地建立模型，提高预测和分类的准确性。本次实验所收集到的学生数据特征不是全部都可用于训练模型，需要从学生数据中提取有用的特征，将无用特征删除。实验进行了以下的特征提取：

删除无用特征：在本次研究中，学生的姓名、学号、年级对于成绩预警来说没有任何帮助，需要将其删除。删除后特征如表1所示。

合并特征：将每个学生的平时成绩和课堂作业成绩特征合并为一个平时成绩特征，合并比例为平时成绩占比60%，课堂作业成绩占比40%；将期中成绩和期末成绩特征合并成为期末成绩特征，合并比例为期中成绩占比40%，期末成绩占比60%。合并后将原始成绩特征删除。合并后如表2所示。

1.3.3  特征编码

特征编码是将数据集中的特征转换为机器学习算法可以理解和处理的形式的过程。在机器学习中，算法只能处理数字化的特征，因此需要将非数字化的特征转换为数字化的形式。特征编码的作用是将非数字化的特征转换为数字化的形式，以便机器学习算法可以对其进行处理和分析，提高模型的准确性和效率，从而提高模型的预测能力。由于学生的性别特征无法直接被用于模型训练，所以需要将特征二值化，男转换为1，女转换为0。本次研究采用Scikit-learn库中的Binarizer类对数据进行二值化。

1.3.4  特征缩放

特征缩放是指将不同特征的取值范围缩放到相同的区间内，常见的缩放方式包括标准化和归一化。特征缩放提高了模型训练的速度和精度，避免异常值对模型的影响，使模型更容易理解。在本次实验中各项数据之间的差距较大，需要对数据进行特征缩放，以保证数据具有可比性。经过多次实验表明，对特征使用标准化缩放所达到的模型效果更适用于本次的研究。

1.3.5  数据集划分

由于在模型构建的过程中需要不断地检验模型的准确率、检验模型的配置及训练程度、过拟合还是欠拟合等，所以需要将训练数据再划分为两个部分，一部分用于训练的训练集，另一部分是进行检验的验证集。验证集可以重复使用，主要用于辅助构建模型，调整模型。在本次实验中，将处理后的数据以8：2的比例划分训练集和测试集。

1.4  模型选择和构建

模型选择和构建是建模的核心环节，该环节的主要任务是选择适合学生数据建模的机器学习模型，不同的模型有不同的假设和约束条件，可以适用于不同的问题和数据集。选择一个合适的模型可以提高预测的准确性和泛化能力，避免过拟合或欠拟合的问题。因此在模型选择和构建过程中，需要考虑模型的准确性、可解释性、泛化能力等因素。

在学生平时成绩数据建模中，常用的机器学习模型包括线性回归模型、决策树模型、支持向量机模型和神经网络模型等。本次研究采用线性回归模型，下面是模型选择和构建的具体步骤。

1.4.1  模型选择

线性回归是一种用于建立变量之间线性关系的模型，该模型假设自变量与因变量之间存在线性关系，即自变量的每一个单位变化都会导致因变量发生相同的单位变化，同时它的系数具有可解释性，可以通过系数的大小和符号来解释不同自变量对因变量的影响程度和方向。在学生成绩预警建模中，因为学生平时各项学习指标会影响学生的期末成绩，所以可以使用线性回归模型来预测学生的学情。线性回归模型的公式如下：

y = β0 + β1 x1 + β2 x2 + … + βn xn

其中，y为因变量，x1、x2、xn为自变量，β0、β2、βn为模型的参数。

在本次研究中，模型的线性回归公式为：

y = θ0 + θ1 x1 + θ2 x2 + θ3 x3

其中，x1为平时成绩，x2为考勤，x3为性别（0或1），θ0、θ1、θ2、θ3为模型参数，y为期末成绩。

1.4.2  模型的构建

模型的构建分为三个步骤：模型拟合、模型评估和模型应用。其中模型拟合的本质是求解上述公式的参数θ0、θ1、θ2、θ3，使用最小二乘法计算预测值与真实值的平方差，即可求解模型的参数，公式如下：

其中，yi为真实值， 为预测值。将模型代入上式，得到：

将上式关于模型参数求导，得到模型参数的最优解：

其中， 为模型参数的最优解，x为数据集的自变量（考勤、性别、平时成绩），y为数据集的因变量（期末成绩）。将  带入公式内，即可实现模型拟合。

在模型拟合之后，需要对模型进行评估，以确定模型的准确性和泛化能力。为了保证实验的严谨，本次研究選择了选择3种评估方式对模型进行评估，包括均方误差（Mean Squared Error， MSE）、均方根误差（Root Mean Squared Error， RMSE）和决定系数（Coefficient of Determination， R2）。

均方误差（MSE）是评估线性回归模型预测效果的常用指标。它计算的是预测值与真实值之间差的平方的平均值。其公式如下：

其中，yi为第i个样本的真实值， 为该样本的预测值，m为样本数。

均方根误差（RMSE）是MSE的平方根，它更直观地反映了预测值与真实值之间的差距。其公式如下：

决定系数（R2）是评估线性回归模型拟合优度的指标，它表示模型能够解释样本数据变异性的比例。其取值范围在0到1之间，越接近1表示模型的拟合效果越好。R2的公式如下：

其中， 为所有样本数据的平均值。

表3是采用MSE、RMSE、R2三种评估方式的结果。

从表中可以看出，该线性回归模型在测试集上的MSE为8.48，RMSE为2.91，R2为0.87，说明该模型具有较高的预测准确性，可以满足实验的初步要求。

在模型评估之后，即模型应用阶段，可将学生平时成绩信息带入模型，模型将预测学生的成绩通过接口传入预警方法中。预警方法通过对预测成绩进行分级，60以下为红色预警，70～79为黄色预警，80～100为绿色预警，当学生预测成绩处于黄色和红色预警阶段，证明该名学生有成绩下降和挂科的风险。

综上所述，模型选择和构建是学生平时成绩数据建模的关键环节。在选择模型时，需要考虑模型的准确性、可解释性、泛化能力等因素，并根据实际需求选择最合适的模型。在构建模型时，需要进行模型拟合、模型评估和模型应用等步骤，以获得准确、稳定和可靠的预测结果。

2  结果验证分析

本次结果验证使用2022级人工智能技术与应用班级28位同学在2022—2023学年第一学期“数据分析”课程数据进行结果验证，并使用预测结果和真实结果进行对比，以下是其中5位学生的预测成绩和实际成绩的数据对比，结果如表4所示。

由表4可得出，学生的期末成绩预测值与实际期末成绩进行对比，预测的成绩与实际的成绩之间的误差较小，预测值可有效地反映学生在学习过程中的成绩情况，说明该模型具有实际的应用价值，可以为学生和老师提供有效的成绩预警。通过分析该模型参数的权重，发现学生的平时成绩对于预测模型的影响最大，考勤和性别的影响相对较小。这也说明了学生的平时成绩是影响学生成绩的重要因素，需要在教学中重点关注和提升。

3  结  论

通过上述实验可以看出，基于线性回归算法构建的学生平时成绩预测模型的预测准确率是可以初步满足学生学情预警的。虽然预测结果存在一定的误差，但整体上预测结果与实际成绩的差距较小。在实际应用中，可以使用该模型来进行学生的成绩预警，及时发现学生的学情问题，提供个性化的学习建议，及时调整学习态度，在一定程度上改善学习状态，从而实现对学生学情的监测和预警。未来，可以进一步改进模型，采用更加复杂的机器学习算法，如决策树、随机森林等，以提高预测的准确性。

参考文献：

[1] 王琪，靳莹.中等教育学段学情分析研究述评 [J].教育理论与实践，2023，43（2）：54-57.

[2] 魏超.机器学习算法在大学生综合素质测评预警中的对比研究 [J].电脑编程技巧与维护，2022（12）：127-129.

[3] 崔争艳，刘晨晨，孙滨.基于机器学习的MOOC学习者弃学预测与预警系统实现 [J].信息与电脑：理论版，2022，34（1）：65-67.

[4] 徐彩凤.依托TPACK理论，推进统计信息化教学——以“一元线性回归模型的应用”为例 [J].中学数学月刊，2023（3）：48-50+63.

[5] 李治軍，姚蓉.基于主成分分析和多元线性回归的黑龙江省用水效率研究 [J].水利科技与经济，2023，29（2）：60-64.

[6] 李非.案例分析在统计多元线性回归预测模型教学中的应用研究 [J].现代职业教育，2019（8）：86-87.

[7] 刘学彦，赵建立，相文楠，等.拟线性回归预测模型的稳定最小二乘解 [J].数学的实践与认识，2011，41（20）：92-97.

作者简介：曹梦川（1990—），男，汉族，宁夏银川人，助教，硕士，研究方向：数据分析、人工智能。

收稿日期：2023-04-09

基金项目：2022年度职业教育研究和开放教育综合改革研究专项课题（XJ202207）；2020年宁夏回族自治区科学技术学会第五批自治区青年科技人才托举工程