实心转子感应电机电磁力特性研究及优化设计

陈 磊

实心转子感应电机电磁力特性研究及优化设计

陈 磊

（海装广州局，广州 510320）

为满足实心转子感应电机在低振动噪声环境下的应用，需对实心转子感应电机进行减振降噪优化设计。本文通过有限元方法，分析定子有槽结构、定子无槽结构、单实心钢转子结构以及实心钢复合转子结构下电机各部件的电磁力分布情况，以振动最小为优化目标，对比分析得出最优的电磁结构。

实心转子 感应电机 电磁力 电机振动 优化设计

0 引言

实心转子感应电机具有优越的启动性能，适合频繁重载启动或长时间工作在制动状态的特点。同时实心转子感应电机具有转子结构简单、机械强度与平衡性高、独特的涡流特性等优点，在起重设备领域，高速电机领域以及多自由度电机等领域具有较高的应用价值[1-2]。

为满足实心转子感应电机在低振动噪声环境下的应用（如舰船和潜艇），需对实心转子感应电机进行减振降噪的优化设计。

对于电机的减振降噪优化设计，已有较为成熟的方法。早在1974年，前苏联学者舒波夫就对电机振动进行了研究，其深入研究了电机振动噪声的三大主要振源，并且在其著作中明确指出，电机的振动主要是由变化的径向电磁力作用在定子齿上而引起[3]。在1998年Cho和Kim两人便针对一台小型鼠笼式异步电机提出了电磁力的计算模型[4]，其分别考虑了转子斜槽、转子偏心，以及开槽对电磁力的影响。Alger和Erdelyri也是较早研究电机振动噪声的学者，其研究结果表明电机振动的主要振源为径向电磁力，并且通过解析计算出了气隙中心线处径向磁密和电机定子的固有频率，在这两者的基础上计算出电机的辐射噪声[5-6]，但是解析公式中存在大量的简化，导致精度较低。

国内关于电机电磁振动噪声的研究起步较晚，诸自强和陈永校两人时国内较早研究电机振动噪声的两位学者，他们对异步电机、同步电机的振动噪声问题进行了深入的研究，提出利用类比的方法将电机的振动计算转换为电路的计算，极大的简化了电机的振动分析[7-8]。在其著作中，系统的阐述了异步电机和同步电机的振动噪声机理，以及电机噪声的鉴别方法和测量方法，并结合异步电机和同步电机本身的固有频率特性提出了多种削弱电磁噪声的措施，如选择合适的定、转子槽配合，斜槽与分数槽等，其研究极大的推动了国内对电机电磁振动噪声问题的研究。

目前电机振动噪声的研究主要集中在永磁电机，对于感应电机电磁力的激振机理以及振动噪声方面的研究还需进一步深入，而针对实心转子感应电机进行减振降噪的优化设计，一方面可丰富感应电机电磁振动理论，另一方面可加快实心转子感应电机在低振动噪声领域的应用。

本文以实心转子感应电机为研究对象，通过有限元方法分析定子有槽结构、定子无槽结构、单实心钢转子结构和实心钢复合转子结构下电机各部件电磁力的分布情况，以振动最小为优化目标，对比得出最优的电磁结构。四种电机结构的拓扑如图1所示，基本的电磁参数如表1所示。

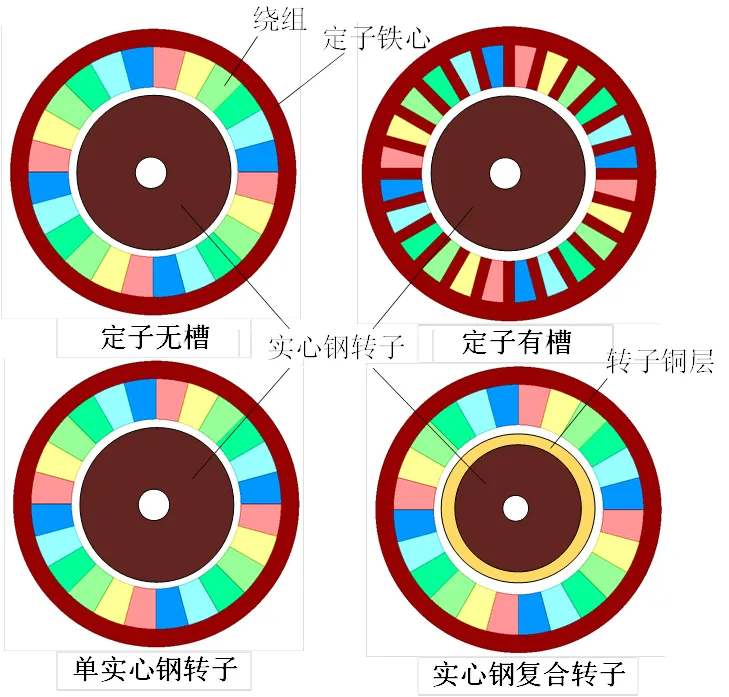
图1 电机拓扑示意图

表1 电机参数

1 电机各部件电磁力计算方法

1.1 定子绕组电磁力计算方法

对于定子绕组，可将其处理为磁场中的载流导体，一般采用洛伦兹力法进行计算，由于单根定子绕组尺寸较小，只需考虑周向集中电磁力与径向集中电磁力。载流导体在磁场中的受力计算公式可以表示为：

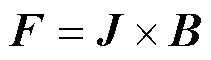
其中表示导体内的电流密度，表示磁感应强度。将绕组截面的电磁力密度进行二维积分，得到单根绕组截面所受集中电磁力。

1.2 定子铁心电磁力计算

定子铁心采用硅钢片叠压而成，由于硅钢片之间相互绝缘，其内部可认为没有涡流回路，仅有磁回路，根据电工理论，定子铁心的主要受力部位为铁心与空气的交界面。

导磁材料在磁场中的电磁力计算可采用Maxwell应力张量法，将体积力等效为面积力，从而简化电磁力计算。由Maxwell应力张量推导的面积力公式为：

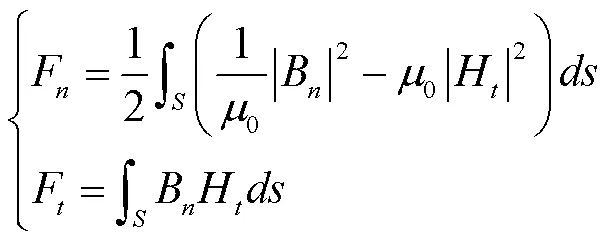
式中，下标表示法向分量，下标表示切向分量，为磁场强度，μ为空气磁导率。

在铁心和空气的交界面上，法向磁感应强度和切向磁感应强度均为连续，但铁心磁导率远大于空气磁导率，因此磁力线进出铁心时几乎与铁心表面垂直，此时H≈0，计算公式可进一步简化为：

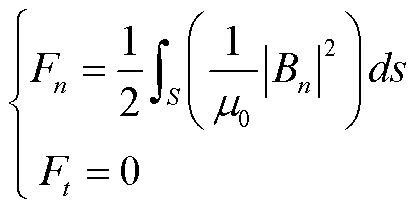
式(3)则表示在定子铁心表面的电磁力方向均垂直于交界面。

1.3 实心转子电磁力计算

根据电工理论，单位体积铁磁物质上所受的电磁力可表示为：

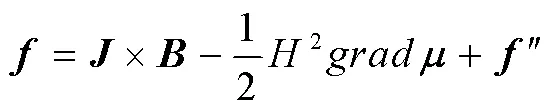
式中，第一项为传导电流在铁磁物质中产生的洛伦兹力，第二项是由磁导率变化而引起的电磁力，第三项为铁磁物质内部发生形变后使磁导率在各个方向发生变化而产生的力，一般磁质形变导致的磁导率变化较小，在通常的计算中可将第三项力略去不计。

实心转子采用实心钢结构，其内部既可以导电也可以导磁。根据式(4)可知，在实心转子内部会受到洛伦兹力，以及磁导率变化产生的电磁力，但在没有达到深度饱和时铁心内部磁导率的梯度较小，可以忽略内部磁导率变化产生的电磁力，因此实心钢内部采用洛伦兹力法进行计算，而对于实心钢表面则采用式(3)进行计算。

2 电机结构对电磁力的影响

2.1 定子开槽对电磁力的影响分析

2.1.1 绕组所受电磁力分析

对于定子开槽电机，绕组的周向电磁力和径向电磁力在不同相位的空间分布关系如图2所示，从图中可以看出单根绕组周向电磁力最大为136 N，径向电磁力最大为1 348 N。因此对于单根绕组而言，径向电磁力会远大于周向电磁力。

在铁心开槽结构下，槽内绝大多数磁力线沿齿部与转子交链，仅存在少量漏磁通穿过定子绕组。其中齿间交链的漏磁通方向主要沿电机周向，因此铁心开槽导致定子绕组上的磁通周向分量远远大于径向分量。而周向磁通决定定子绕组径向电磁力，所以单根绕组中径向电磁力大于周向电磁力。

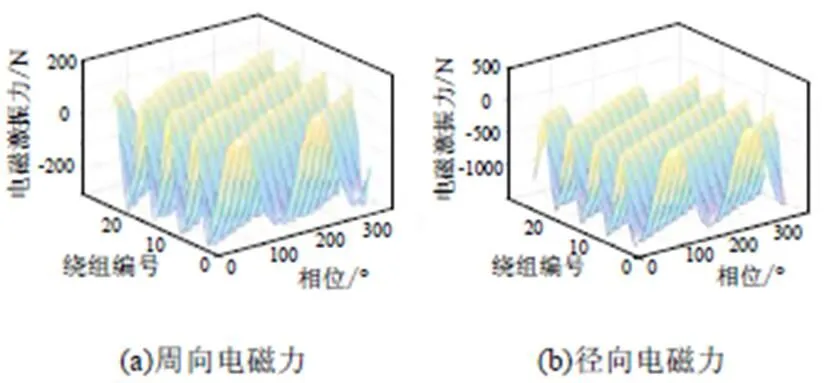
图2 定子开槽绕组电磁力空间分布

对于定子无槽电机，绕组的周向电磁力和径向电磁力在不同相位的空间分布关系如图3所示。从图中可以看出单根绕组周向电磁力最大值为1 748 N，径向电磁力最大值为418 N。因此对于无槽电机的单根绕组而言，周向电磁力远大于径向电磁力。因为采用无槽定子后，绕组中主要为径向磁通，而周向电磁力主要由径向磁通决定，因此在定子无槽电机中单根绕组的周向电磁力会大于径向电磁力。

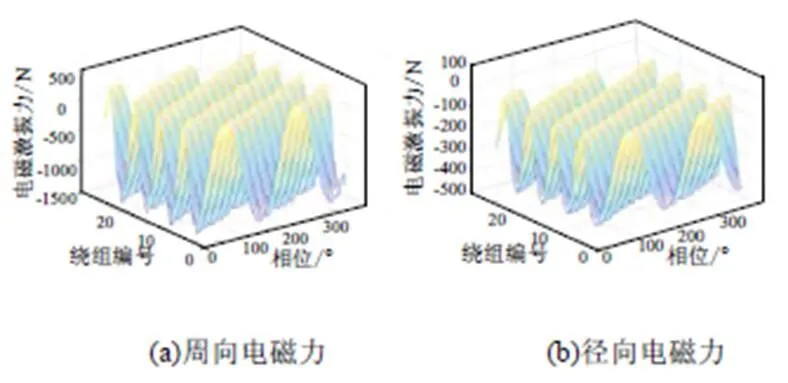
图3 定子无槽绕组电磁力空间分布

通过对比分析以上结果可以得出，定子开槽电机绕组电磁力径向分量大于周向分量，而定子无槽电机绕组电磁力周向分量大于径向分量。

2.1.2 定子铁心所受电磁力分析

对于定子开槽电机，主磁通经过定子齿部与动子交链，定子齿部是主要受力部位。以1号和2号绕组中间的定子齿部为对象，利用Maxwell应力张量法，求解得到齿顶和齿壁电磁力的法向集中力和切向集中力如图4、图5所示。其中齿顶的法向力为径向力，切向力为周向力，而齿壁的法向力为周向力，切向力为径向力。

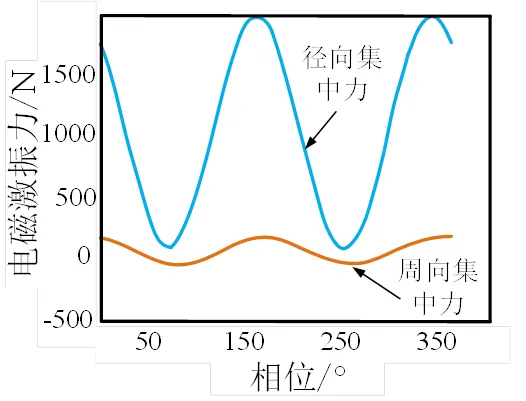
图4 定子齿顶电磁力

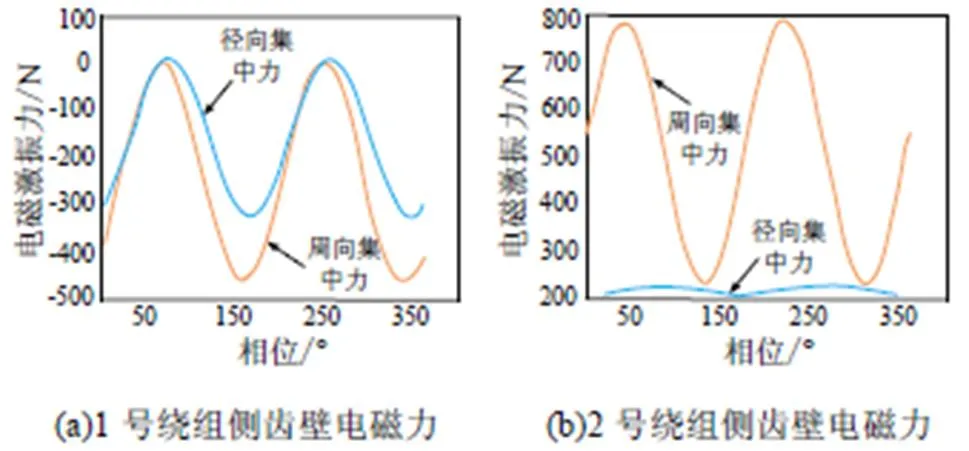
图5 定子齿壁电磁力

齿顶和齿壁的电磁力沿法向分量较大，表现为齿顶主要受力沿径向正方向，齿壁主要受力沿周向。同一齿两侧齿壁受力大小不等，若1号绕组侧齿壁周向电磁力为F，2号绕组侧齿壁周向电磁力为F，则齿部周向电磁力为F-F。

对于定子无槽电机，铁心形状规则，电磁力集中在定子铁心靠近绕组的交界面。定子铁心与定子绕组间存在气隙，根据Maxwell应力张量法，定子铁心与空气交界面上切向力为零，交界面周向和径向力密度如图6所示。

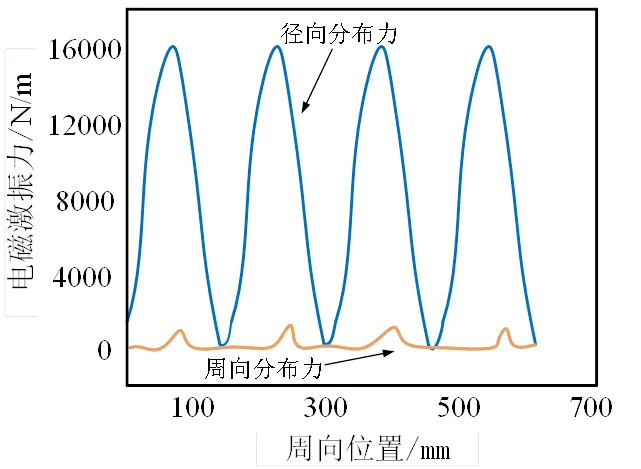
图6 定子无槽铁心电磁力密度分布

定子有槽和定子无槽结构下，定子铁心所受径向电磁力分布如图7所示。

从图4～7中可以对比得出，有槽结构定子所受的径向电磁力大于无槽结构定子所受的径向电磁力，且有槽结构电磁力的空间阶次更为丰富。

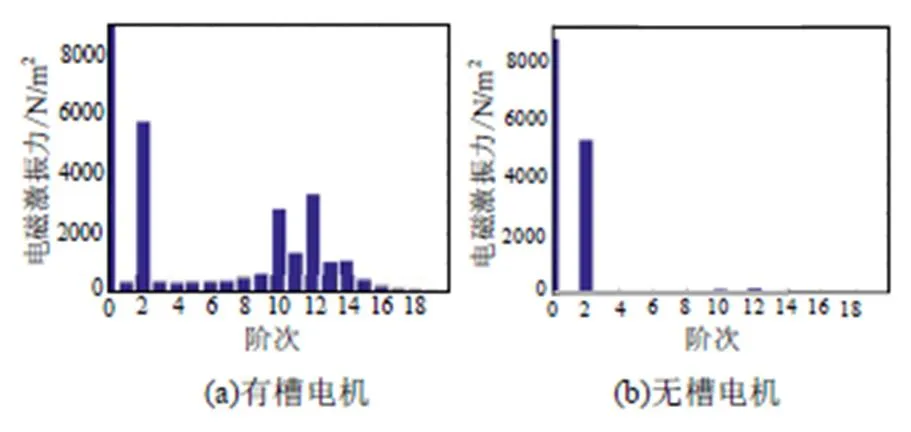
图7 定子铁心电磁力空间阶次分布

2.1.3 实心转子所受电磁力分析

对于定子开槽电机，实心转子径向电磁力的空间分布和空间阶次分布如图8所示。

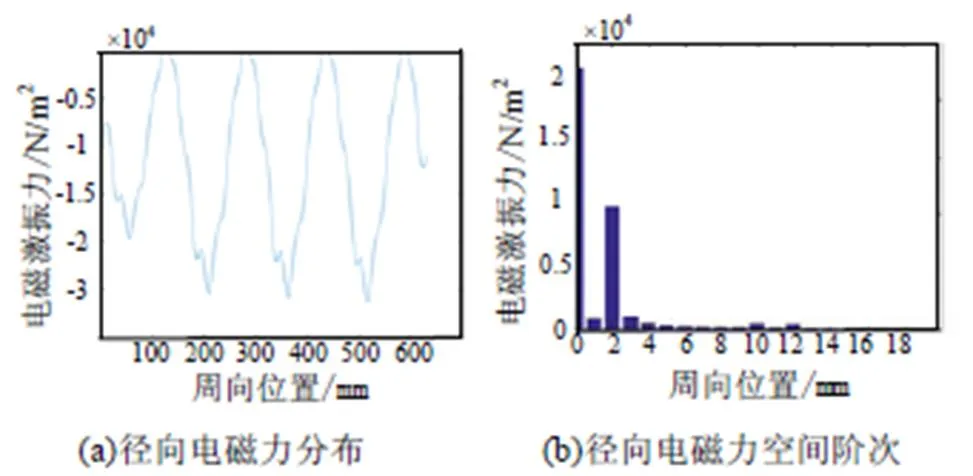
图8 定子开槽下实心转子径向电磁力分布

对于定子无槽电机，实心转子的径向电磁力的空间分布及空间阶次分布如图9所示。

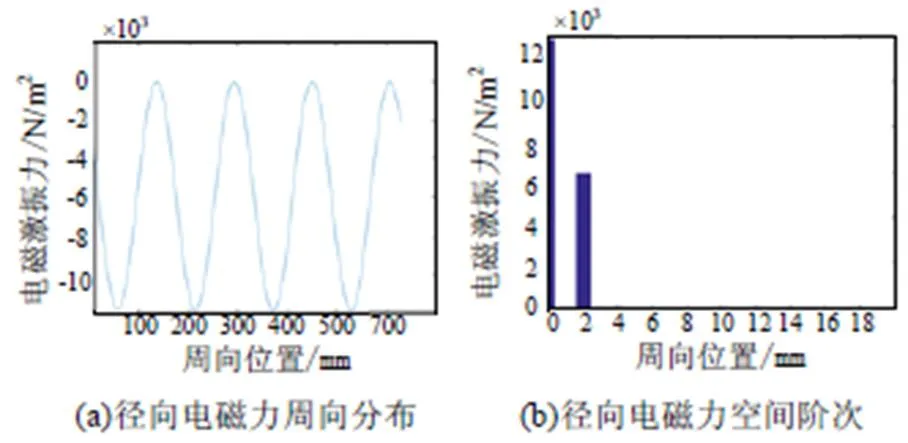
图9 定子无槽下实心转子径向电磁力分布

对比定子开槽和定子无槽结构下实心转子的径向电磁力，可以分析得出定子无槽结构下实心转子径向电磁力主要包括0阶分量与2阶分量，而定子开槽结构下实心转子径向电磁力密度包含0-14阶分量，其中0阶、2阶、10阶和12阶分量幅值较大，造成电磁力空间阶次丰富的主要原因是定子齿槽带来的齿槽谐波所致。

定子开槽结构下实心转子径向分布力幅值为26 410 N/m2，定子无槽结构下实心转子径向分布力幅值为11 890 N/m2。可见定子开槽结构下实心转子径向分布力大于定子无槽结构下实心转子径向分布力。

2.1.4 综合对比分析

输入电流有效值1 000 A时，定子开槽电机产生的周向合力为21 641 N，定子无槽电机产生的周向合力为11 323 N。已知周向合力与电流平方成正比，因此定子开槽电机和定子无槽电机产生10 kN周向合力时，输入电流的有效值分别为679.77 A和939.76 A。在产生相同周向合力的前提下，定子开槽电机和定子无槽电机实心转子受力数值计算结果对比如表2所示。

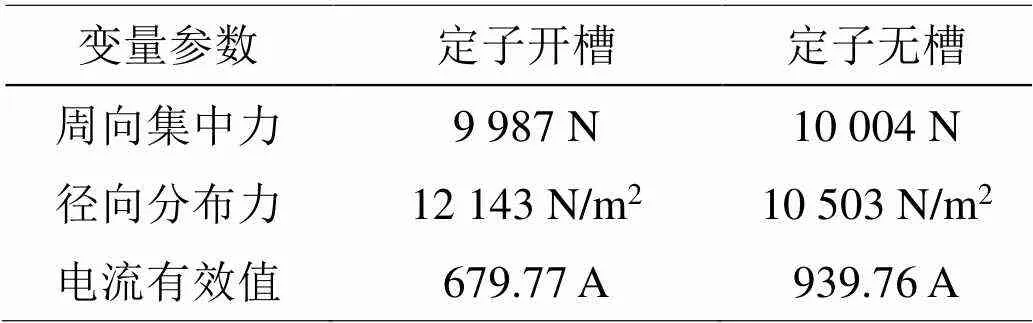
表2 有槽和无槽结构下转子受力对比

从表2中可以得出，在相同周向合力输出时，定子无槽电机实心转子的径向分布力小于定子开槽电机实心转子的径向分布力，且定子有槽电机的电磁力谐波成分更为丰富，而径向分布力是造成转子振动的主要激励源，因此在输出相同周向合力的情况下定子开槽电机径向电磁力更大且空间阶次更丰富，引起的电磁振动更大。

对于定子侧，造成定子振动的主要激励源是定子铁心径向电磁力和定子绕组径向电磁力，根据图2和图3的对比分析，定子开槽电机的径向电磁力（单根绕组径向力和定子铁心径向力）均大于定子无槽电机径向电磁力，再对比图7(a)和图7(b)电磁力的空间阶次，得出有槽电机定子铁心所受电磁力的谐波阶次更为丰富，引起的电磁振动更大。

综合对比，从振动最小的优化目标出发，应选择定子无槽结构。

2.2 转子结构对电磁力的影响分析

本节分析两种转子结构对电机各部件电磁力的影响。由于在2.1节中分析得出，定子无槽结构有利于减振，因此后续将基于定子无槽结构进行分析。

2.2.1 绕组所受电磁力分析

单实心钢转子结构下绕组电磁力的空间分布以及实心钢复合结构下绕组电磁力的空间分布与图2、3相似。对于单实心钢转子结构，单根绕组周向集中力峰值为2 866 N，径向集中力峰值为205 N。对于实心钢复合转子结构，单根绕组周向集中力峰值为1 686 N，径向集中力峰值为423 N。通过对比分析可以得出，两种转子结构单根绕组的周向电磁力均大于径向电磁力，因为定子绕组磁通分布主要受定子铁心结构的影响，转子结构不改变定子绕组电磁力在周向和径向大小规律。

2.2.2 定子铁心所受电磁力分析

定子铁心为无槽硅钢片叠压结构，电磁力集中在定子铁心靠近绕组侧的边界上。单实心钢转子和实心钢转子结构下定子铁心的周向电磁力分布和径向电磁力分布和图6相似，两者周向电磁力密度均为零，单实心钢转子结构下定子铁心的径向电磁力幅值为42 470 N/m2，实心钢复合转子结构下定子铁心的径向电磁力幅值为14 790 N/m2。可见单实心钢转子径向电磁力密度更大，产生的振动也会相应增大。

2.2.2 实心转子所受电磁力分析

对于单实心钢转子电机，首先计算得出周向集中力为2665N。而对于径向电磁力，主要由转子铁心表面的径向电磁力和内部的径向电磁力构成，根据Maxwell应力张量法可以计算得到表面的径向电磁力分布如图10(a)所示。

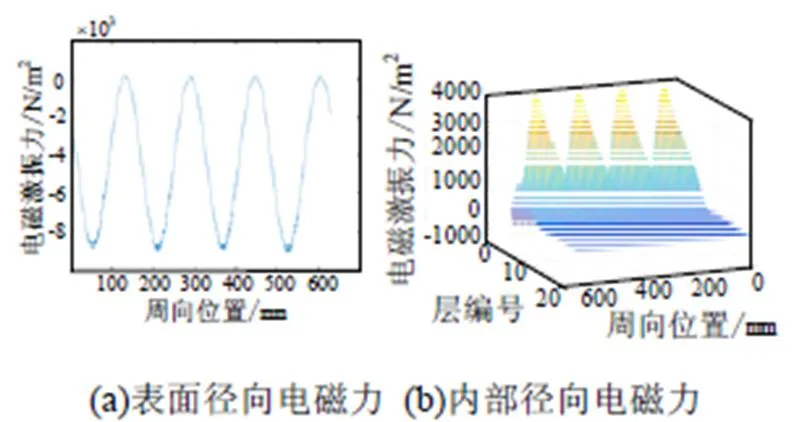
图10 单实心钢转子径向电磁力分布

对于单实心钢转子内部径向电磁力，由于集肤效应的影响，实心钢转子内部的涡流沿径向的变化不可忽略，因此需对实心钢转子沿径向进行分层处理，进而分析不同径向位置下电磁力的分布情况。根据转子径向长度，将其沿径向分为19层，并将每一层编号为1～19。计算得到不同径向长度上电磁力的分布情况如图10(b)所示，从图中可以看出1～19层，电磁激振力呈逐渐减小趋势。其原因在于实心钢转子的集肤效应，感应涡流集中在实心钢转子的外表面，导致越靠近外表面的电磁激振力越大。

将磁导率变化引起的电磁力与内部涡流引起的电磁力通过积分进行叠加，求得单实心钢转子径向合成电磁力在周向依然呈正弦分布与图10(a)相似。从图10中可以看出，转子表面电磁力与内部电磁力有一定抵消，但从径向合成力来看大多数区域受力方向为径向正方向，且径向电磁力幅值为3 741 N/m2。

对于实心钢复合转子，其铜层和钢层上均受到电磁力作用，根据洛伦兹力公式，实心钢复合转子上铜层电磁力的周向集中力为10 437 N，径向电磁力沿周向分布，幅值为2 495N/m2。

而对于钢转子部分，其周向集中力为547 N。将钢转子按径向长度分解为15层，并沿径向编号为1-15。根据Maxwell应力张量法和洛伦兹力法计算得到钢转子表面的径向电磁力如图11(a)所示，内部的电磁力如图11(b)所示。

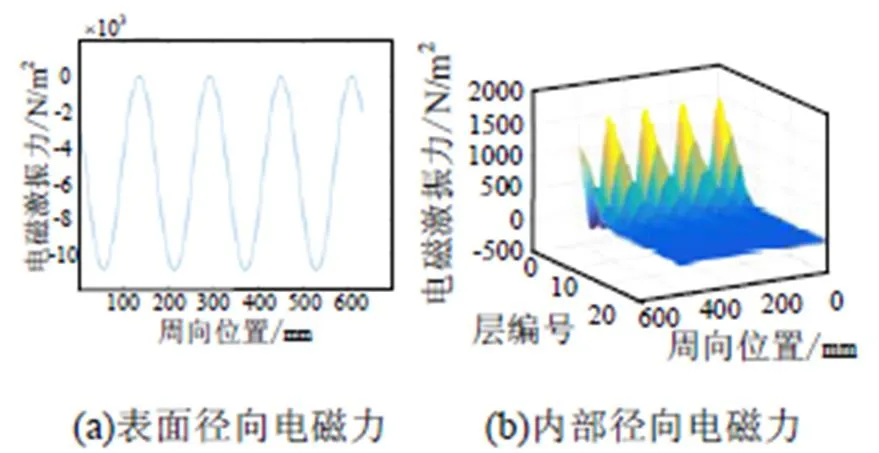
图11 复合实心钢转子径向电磁力分布

将磁导率变化产生的径向电磁力与涡流产生的径向电磁力沿径向进行积分叠加得到钢转子合成径向电磁力分布，幅值为9 933 N/m2，受力方向以径向负方向为主。

2.2.4 综合对比分析

在定子无槽的前提条件下，当输入电流有效值为1000 A时，单实心钢转子和实心钢复合转子电磁力对比如图表3所示。

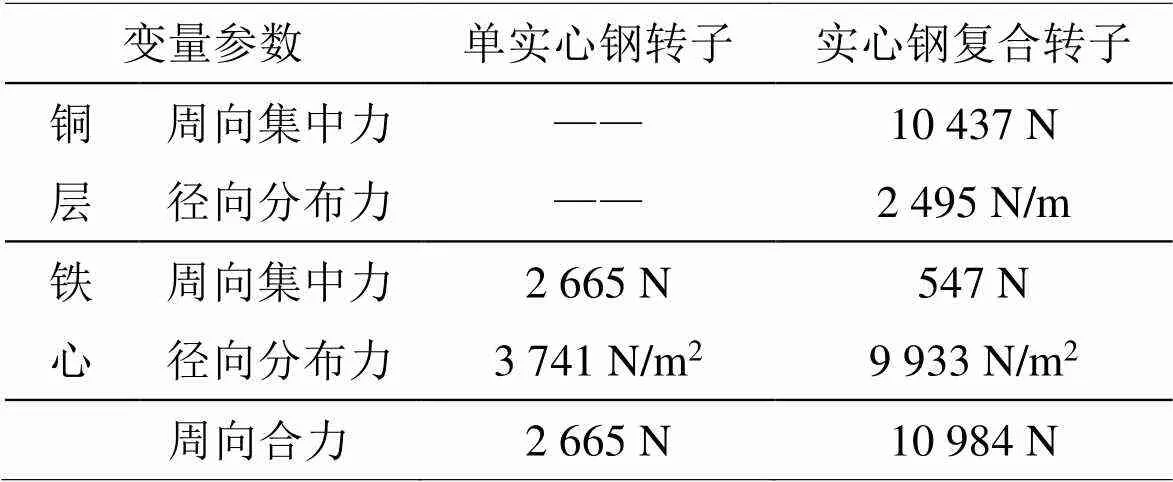
表3 相同电流输入下两种转子结构受力对比

若两种电机输出相同10 kN的周向合力，输入电流有效值分别为1 937.1 A、939.76 A。输出相同周向合力时，单实心钢转子电机和实心钢复合转子电机电磁力数值计算结果如表4所示。

在输出相同周向合力时，单实心钢转子电机径向电磁力大于实心钢复合转子电机的径向电磁力，其中实心钢复合转子中铜层为主要受力部件。因此在输出相同周向合力时，实心钢复合转子电机产生的径向电磁力最小，以振动最小为优化目标，应选择实心钢复合转子。

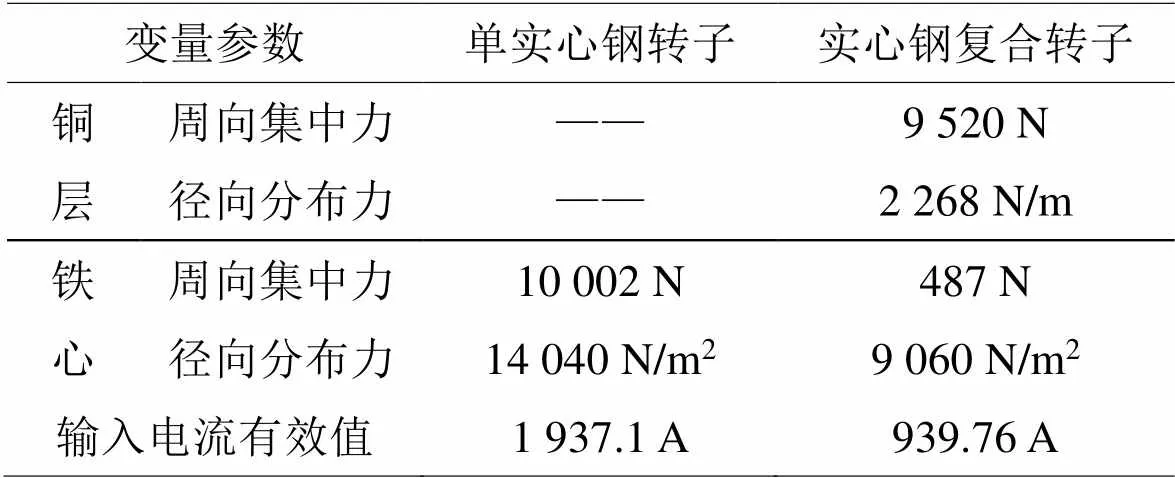
表4 相同周向合力输出下两种转子结构受力对比

3 结论

本文利用有限元分析方法，计算并分析了定子有槽结构、定子无槽结构、单实心钢转子结构和实心钢复合结构下各部件电磁力的分布，并针对导电导磁材料的电磁力计算，提出了根据导电性和导磁性分解计算后叠加分析的思路。

分析发现如下规律：

定子无槽电机径向电磁力空间阶次主要包含0阶分量和2阶分量，定子开槽电机径向电磁力空间阶次主要包含0阶、2阶、10阶和12阶分量，定子开槽电机电磁力谐波阶次分布更为复杂。而转子结构由于采用光滑结构，单实心钢转子和实心钢复合转子均不会对磁场引入高阶谐波分量。

在输出相同周向合力时，不同定子结构和转子结构产生的电磁力大小关系为：定子开槽电机所受电磁激振力大于定子无槽电机所受电磁激振力，单实心钢转子电机所受电磁激振力大于实心钢复合转子电机所受电磁激振力，因此综合对比电机应选择定子无槽，转子实心钢复合结构。

[1] 王培欣, 司纪凯, 封海潮, 等. 实心转子感应电机研究与发展概况(上)[J]. 微特电机, 2017, 45(8): 77-82.

[2] 王培欣, 司纪凯, 封海潮, 等. 实心转子感应电机研究与发展概况(下)[J]. 微特电机, 2017, 45(9): 82-86.

[3] 舒波夫. 电机的噪声和振动[M]. 沈官秋, 译. 北京: 机械工业出版社, 1980.

[4] Cho D H, Kim K J. Modelling of electromagnetic excitation forces of small induction motor for vibration and noise analysis[J]. IEE Proc - Elec Power Appl, 1998, 145(3): 199-205.

[5] Erdelyi E. Predetermination of sound pressure levels of magnetic noise of polyphase induction motors [includes discussion][J]. Trans Am Inst Electrical Engineers. Part III: Power Appar Syst, 1955, 74(3): 1269-1280.

[6] Alger P L. The magnetic noise of polyphase induction motors[J]. Electr Eng, 1954, 73(6): 497-497.

[7] 陈永校. 电机噪声的分析和控制[M]. 杭州: 浙江大学出版社, 1987.

[8] 陈永校, 诸自强. 电机振动分析中的机电类比[J]. 电机技术, 1985(3): 29-32.

Study of electromagnetic force characteristics and optimal design of solid rotor induction motor

Chen Lei

(Naval Equipment Department in Guangzhou, Guangzhou 510320, China)

TM346

A

1003-4862（2023）11-0012-06

2023-04-12

陈磊（1985-），男，硕士，研究方向：装备监造。E-mail：604326870@qq.com