高性能永磁同步电机显式模型预测控制算法研究
刘忠永 范 涛 何国林 温旭辉
高性能永磁同步电机显式模型预测控制算法研究
刘忠永1,2范 涛1,2何国林2温旭辉1,2
(1. 中国科学院大学 北京 100049 2. 中国科学院电工研究所 北京 100190)
该文提出一种应用于永磁同步电机的级联式高性能显式模型预测控制算法,基于多参数规划思想建立系统参数化模型,离线求解有约束条件下的最优解并以状态量的分段仿射函数形式保存,解决了连续控制集模型预测控制算法在线求解的算力需求问题;全面介绍了显式模型预测控制的应用思想及设计流程,分析了在永磁同步电机控制中模型失配、死区效应、数字延时等非理想因素带来的影响并给出了应对措施;与传统PI控制算法进行对比,通过仿真与实验验证了显式模型预测控制算法的有效性及优越性。
永磁同步电机(PMSM) 显式模型预测控制 最优化控制 转速预测控制 电流预测控制
0 引言
在新世纪“双碳”国家能源战略大背景下,伴随着“电动化、智能化、网联化”相互赋能,我国的电动汽车产业发展已经进入了一个崭新的阶段。
在三电之一的电机控制领域中,过去数十年间应用最为广泛的PI控制策略属于经典的多环路控制策略(multiloop control)[1],基于误差调节的控制思想使其具有较强的普适性,但是也仍然存在一些问题:PI控制的增益系数通常只在特定的工作区内表现优异,缺乏针对电机状态变化的优化考虑[2];电机d、q轴之间的耦合项被定义为扰动,前馈交叉解耦等策略将影响到系统的动态性能[3];控制量的选择没有考虑到系统的约束条件,如定子电流大小以及电压源逆变器的最大可输出电压,限制了电驱系统的性能及效率,且由于积分控制器的存在,抗饱和策略的引入可能会导致线性系统的不稳定[4]。
20世纪70年代于过程工业提出的预测类控制算法标志着业界控制思想开始由调节向寻优方向的转变,从基于脉冲、阶跃响应模型的预测算法[5-6]到广义预测控制(General Predictive Control, GPC)的提出[7-8],再到结合最优化控制以及李雅普诺夫稳定性思想的综合性理论,经过数十年的发展,模型预测控制(Model Predictive Control, MPC)算法已经成为针对多输入多输出、具有复杂约束条件的非线性动态系统的有效控制策略,其实现思想是在每一个控制周期内,基于系统预测模型及当前的状态量(测量值或估计值),求解代价函数(cost function)在预测时域内最优的控制序列,选取第一个控制量作用于控制对象,并不断重复该过程。然而,受限于MPC对于寻优问题的巨大算力需求,直到近些年来,随着计算处理单元的迅速发展和各类新算法的提出,才开始广泛应用于电力电子和电机控制领 域[9]。
永磁同步电机(Permanent Magnet Synchronous Motor, PMSM)控制领域中,根据是否需要脉冲宽度调制(Pulse Width Modulation, PWM)技术,MPC分为有限控制集(Finite Control Set, FCS)及连续控制集(Continuous Control Set, CCS)两类[10]。FCS直接以逆变器开关组合为控制动作,遍历求解使得代价函数最优的开关状态,并延伸出了一系列优化算法,如多矢量控制[11-17]、多步控制[18-19]等;CCS控制策略依赖PWM技术,基于系统模型及代价函数求解一个最优化控制问题,最优控制量以幅值及相位皆连续可调的电压矢量表达,保证了固定的开关频率。最优化控制问题一般为无约束或有约束的二次规划形式,对于无约束问题,基于代数黎卡提方程求解的最优控制量具有解析解形式,此类控制方法也被称之为线性二次型调节器(Linear Quadratic Regulator, LQR)。对于有约束问题,由于约束条件的复杂性,其最优解不存在解析解形式,可以通过一些数值求解方法求得近似最优的数值解,如梯度投影法、内点法、有效集法等,但是对于电机系统此类响应时间要求较快的控制对象,很难在较短的控制周期内完成对于目标问题的迭代求解[20]。显式模型预测控制(Explicit Model Predictive Control, EMPC)思想的提出[21],将有约束问题在线求解的数值解形式转化为离线关于状态量的分段仿射(Piecewise Affine, PWA)函数显式表达,有效地解决了MPC在线求解困难的问题。
本文提出一种基于EMPC思想的高性能永磁同步电机控制策略。采用多参数规划思想分别建立电流控制及转速控制的系统线性化模型,消除状态之间的耦合及非线性环节影响,离线求解在有效约束条件下使得代价函数最优的控制量并以分段仿射函数的形式保存,实际运行中通过查询当前状态量组合所在分区,获取对应的最优控制量。对MPC应用中的模型失配、数字延时、死区效应等问题进行了全面分析并给出了相应的解决方案,基于一套全自动对拖测试平台验证了算法的有效性。
1 显式模型预测控制
MPC的三大组成要素分别为:预测模型、代价函数、滚动优化,定义线性时不变系统预测模型为
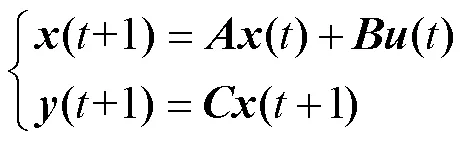
式中,、、为系统常系数矩阵;、分别为系统的状态及控制向量;为时间。
、的维度及约束条件定义为
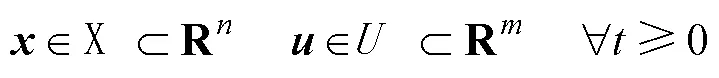
假设系统在时刻所有状态量皆可测量或可估计得到,定义预测时域(→+)内的有约束有限时间尺度最优化控制(Constrained Finite Time Optimal Control, CFTOC)问题(在MPC中称之为代价函数)为
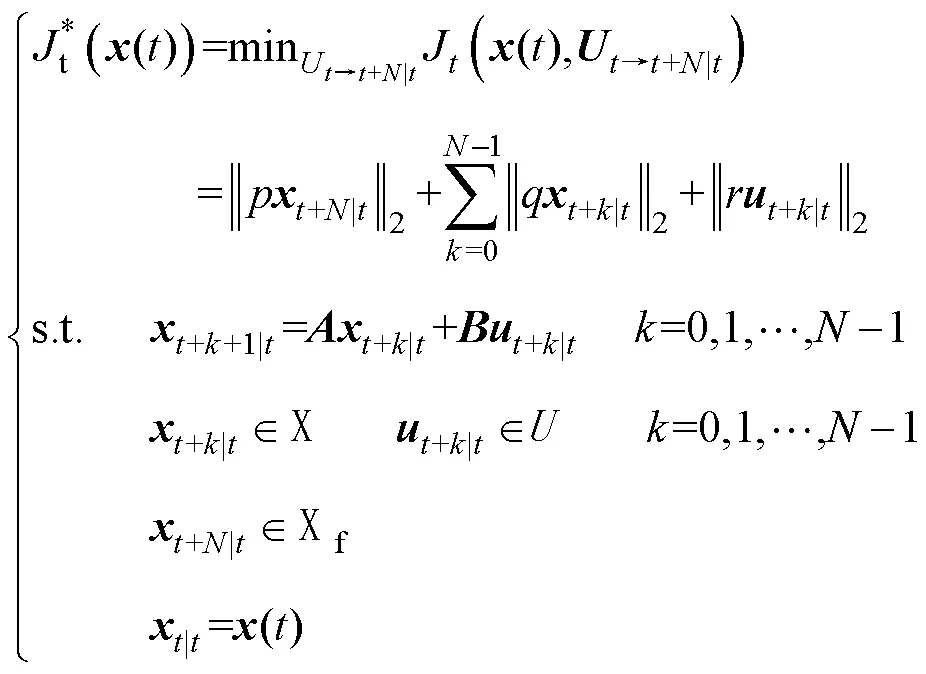
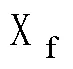

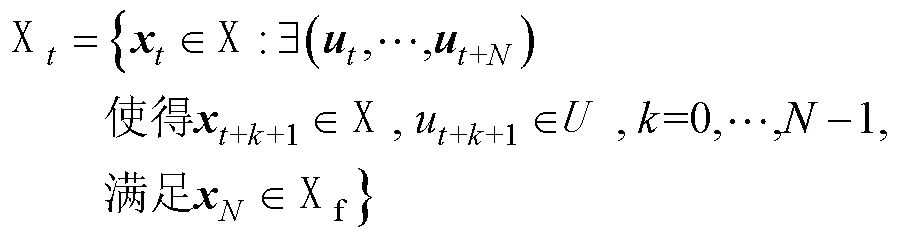
对于可行集内的任意状态量都可以求得最优控制量,使得在预测时域内的状态量满足约束条件。
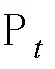
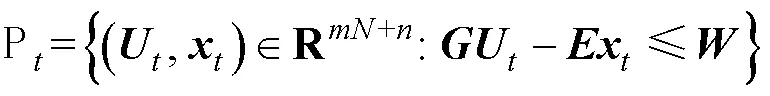
式中,、、为系统约束矩阵。
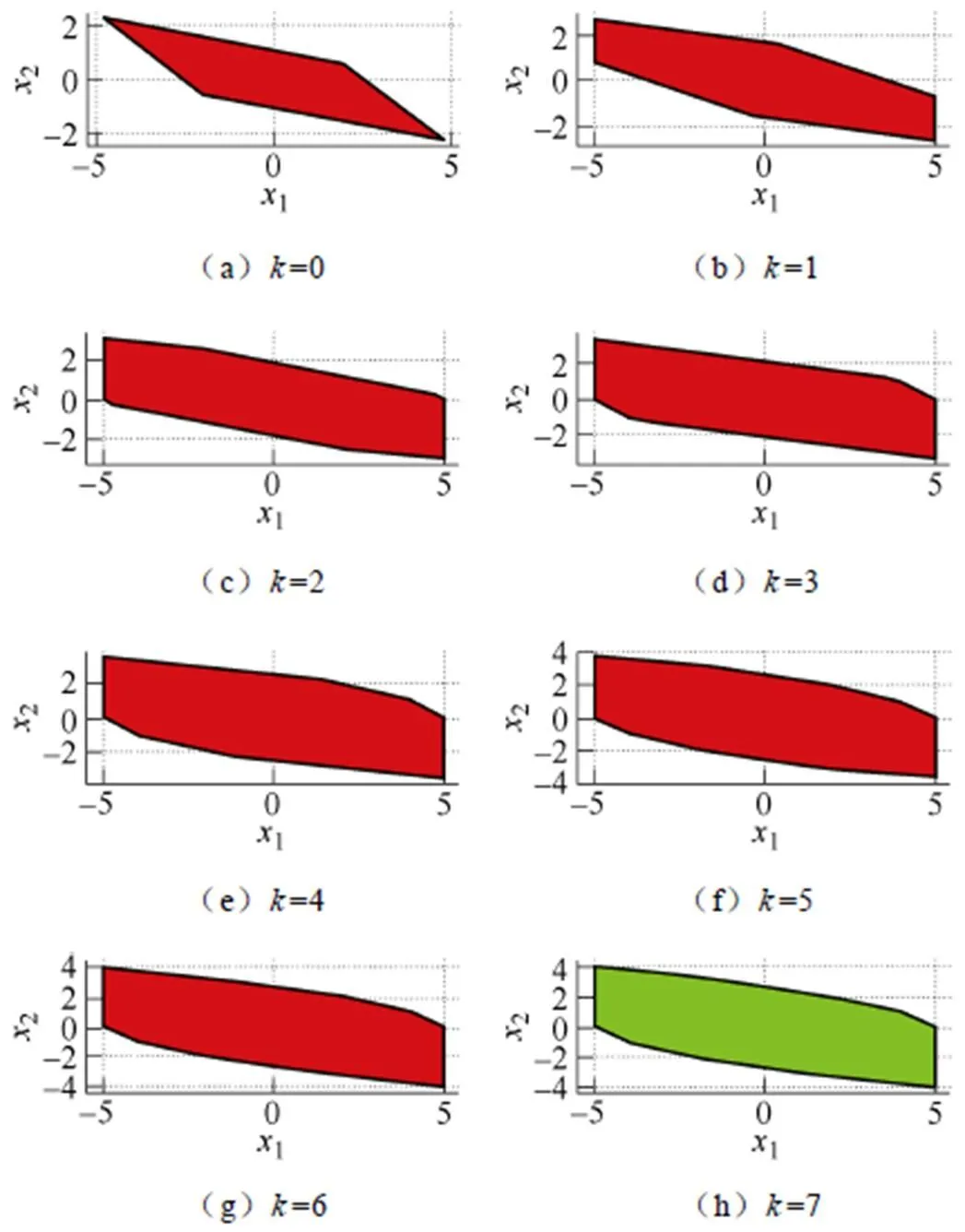
图1 控制不变集的迭代求解
将线性系统本身定义的等式约束代入到代价函数中,采用批处理法将待求的多时间尺度问题转化为基于系统当前状态值() 的单时间尺度内的多维控制问题,有

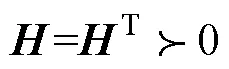
定义时刻的新控制变量如式(7)所示,为原问题控制量及状态量()的线性仿射组合,则式(6)所示原问题可转化为标准的二次规划形式如式(8)所示。
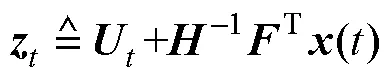
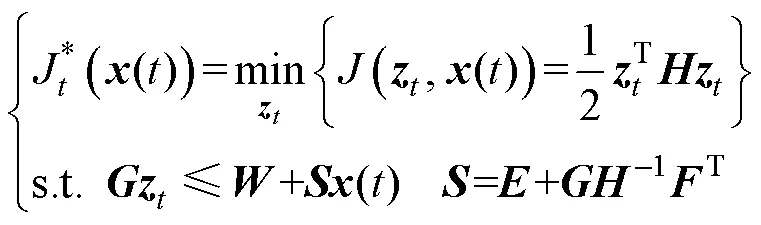
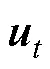
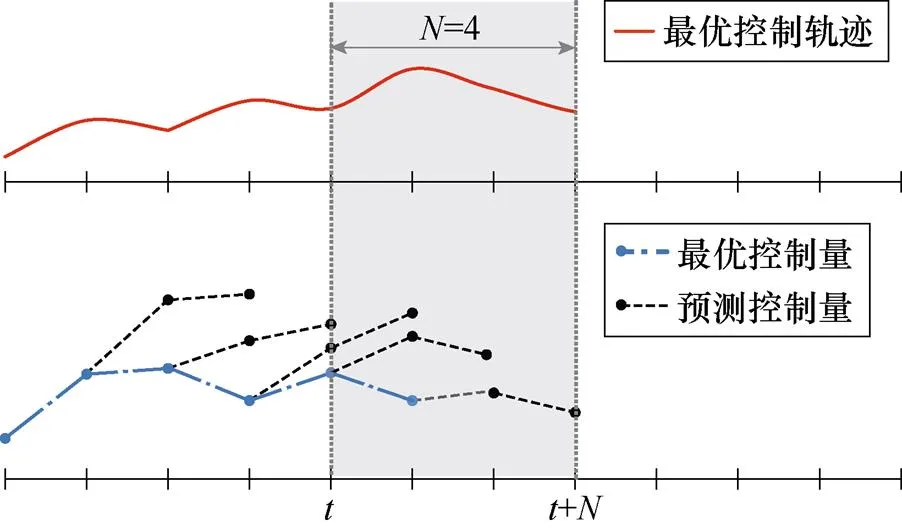
图2 滚动时域控制
对于式(8)所示的CFTOC问题,基于运筹学中的多参数规划理论将其转化为多参数二次规划问题(Multiparametric Quadratic Program, Mp-QP)。将状态量看做参数,研究在整个状态范围内的最优解变化趋势,根据Karush-Kuhn-Tucker(KKT)条 件[22]离线求出在不同状态组合下的最优解,显含状态量为

Mp-QP的最优解存在两种情况:在约束条件内部或者在约束条件边界上。根据最优解是否触发约束条件进行临界区域(Critical Region, CR)划分如式(10)所示,A()为最优解处于约束条件边界时的分区,NA()为最优解在约束条件内部时的分区。
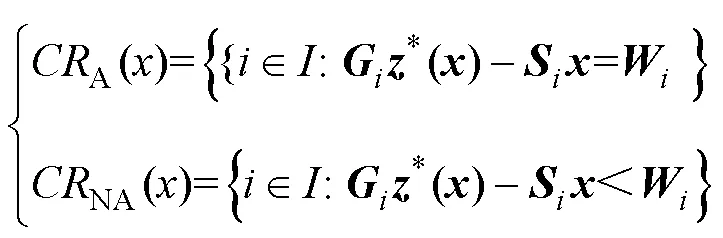
对于在NA()分区内的最优解,原问题等效为LQR问题,不再过多讨论。对于约束条件成立的最优解分区A(),基于KKT条件求得在不同约束条件成立下的最优解为
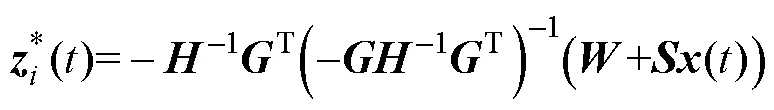
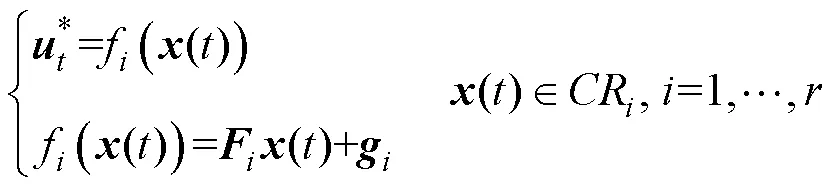
式中,f为仿射函数关系;、分别为在分区内最优解和状态量的仿射系数。
EMPC的实现思想完全涵盖RHC的理念,实现逻辑如图3所示,离线计算在不同状态分区下的CFTOC问题最优解,确定在状态空间上关于最优解的显式函数表达,在线控制算法基于状态当前值确定所属临界分区从而得到对应的仿射控制律,只取预测时域内的第一个控制量,作用到系统完成控制。最优控制律以PWA的形式储存在处理器中,由于函数调用中只有乘加运算,不含除法,且分区查询代码也较为简单,大大提高了MPC应用的便利性。
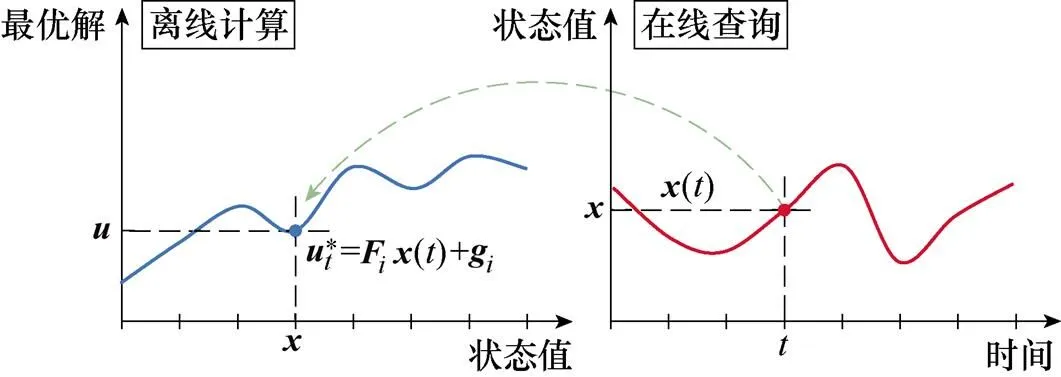
图3 EMPC控制逻辑
2 EMPC设计
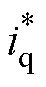
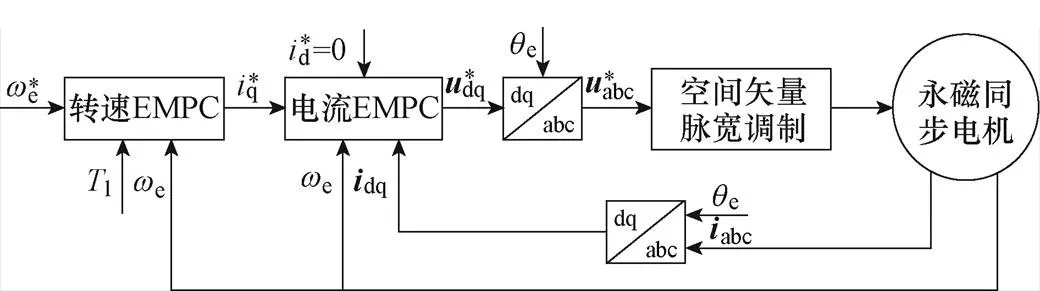
图4 EMPC电机控制框图
2.1 离散化控制模型
EMPC设计第一步是确定系统预测模型及代价函数,PMSM离散化电流控制模型为
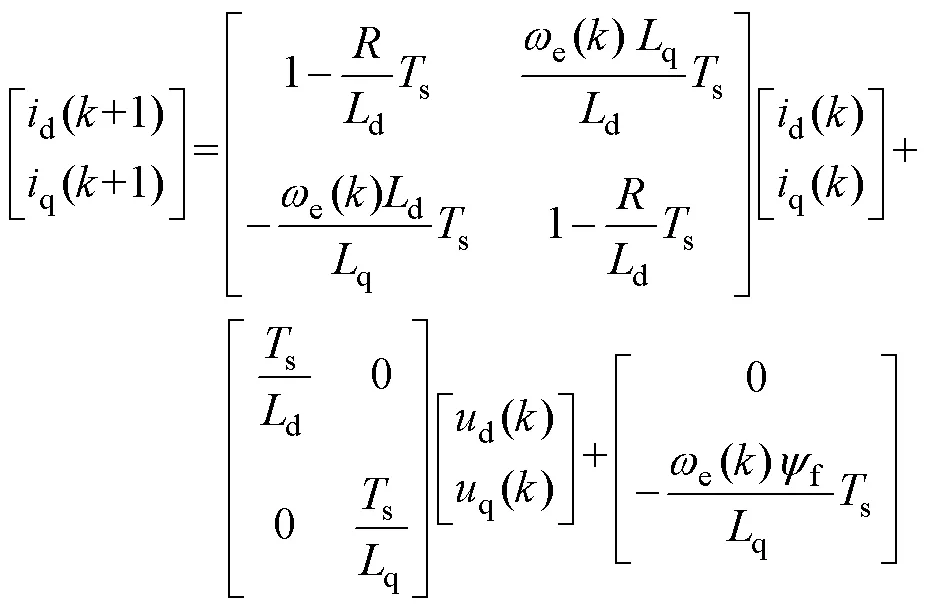
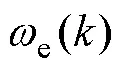
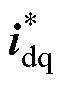


预测模型确定后要定义代价函数,以求得在预测时域满足控制目标的最优控制量,定义EMPC电流控制代价函数为
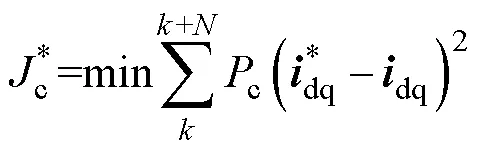
式中,c为电流控制权重系数。
EMPC电机转速外环模型为

在电机级联控制中,转速外环的输出为电流内环的q轴电流指令,以转速跟踪为控制目标,定义转速外环代价函数为

式中,s为转速控制权重系数。
预测模型的建立需要考虑离散步长,离散步长越小意味着模型越精确。确定了预测时域及代价函数后,模型离散步长直接表征预期的响应时间及控制量大小,因此首先要考虑控制对象的时间常数,避免出现控制量更新频率太快而系统无法响应的情况。对于电机系统而言,内外环的时间常数差异较大,采用非级联控制可能会出现二者性能难以兼顾的问题,级联控制方式的优势体现在可以对内外环选用不同的离散步长以满足各自需求。本次实验功率器件选择ABB公司的5SNG 1000X170300的IGBT,开关频率设置为5 kHz,电流、位置、转速等参与控制信息的采样频率设置为5 kHz,电流环电气时间常数较小,能够实现较快的动态响应,与逆变器频率保持一致为5 kHz,转速环机械时间常数较大,可选择数倍慢于内环的控制频率运行,经多次仿真与实验,设置为500 Hz,有

此外还需要考虑预测时域的选择,其表示对于系统未来状态预测的拍数,等于待求解最优化控制问题及最优解的维度,s表示在本次求解中待预测的绝对时间跨度,因此越长,对于系统未来的预测越全面,随之也会加剧问题求解的难度,导致临界分区数激增,由于RHC策略的存在,预测时域只需要能够包含系统动态特性即可。对于级联控制而言,无论是从电压指令给出到电流响应,还是从电流指令给出到转速响应,考虑到数字控制的延迟特性,选择预测时域=3可保证对于系统未来实现完整的预测。值得一提的是,由于约束条件的存在,使得跟踪误差最小的最优解未必能在预测时域内完成指令跟踪。
2.2 约束条件
EMPC中以不等式约束形式对状态量及控制量限定边界,纳入到最优化控制问题的求解。电机系统在工作中受到的主要约束为电压及电流约束,电压约束是指电机最大输出电压受到电源限制,电流约束由电机温升和功率器件所决定,有
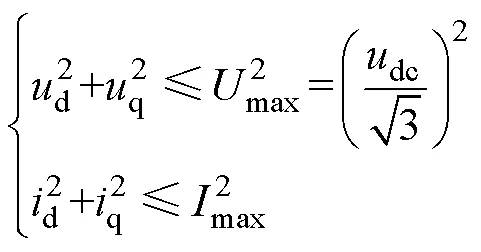
式中,dc为直流母线电压;max为逆变器基于SVPWM方法能产生的最大相电压峰值;电流约束由电机温升和功率器件所决定,max为电机相电流最大值。
EMPC问题不能处理如式(19)所示的非线性约束,以多边形近似的方式将其转化为线性约束如式(20)所示,EMPC电压及电流约束限制如图5所示。
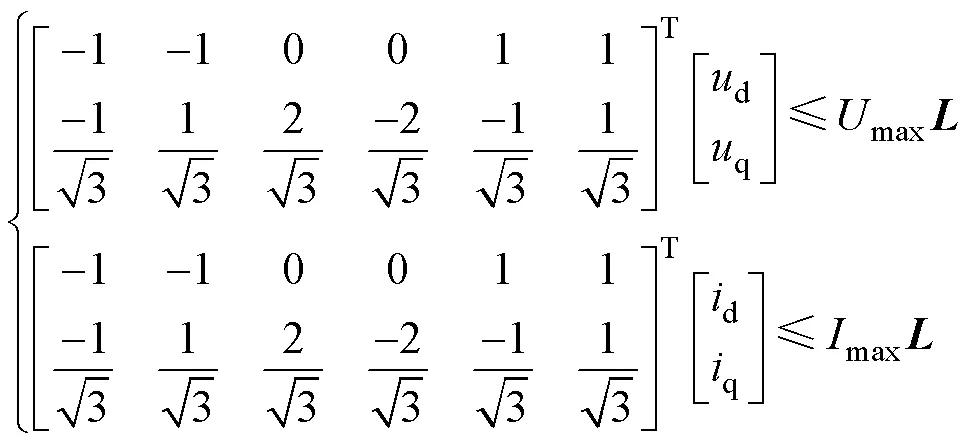
其中
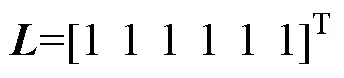
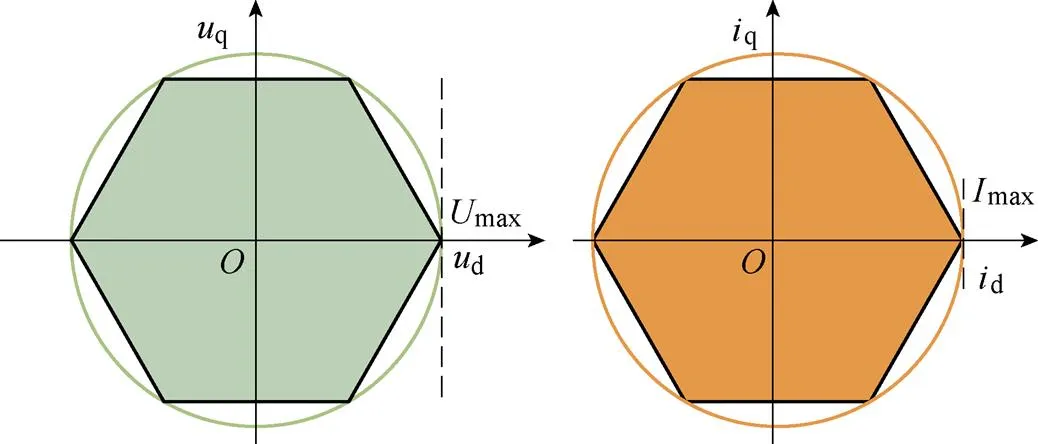
图5 电压及电流约束
转速外环控制在电流约束的基础上,定义转速约束以及负载转矩约束为
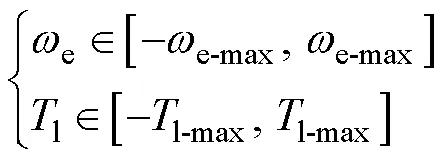
2.3 参数失配
由于约束条件的存在,EMPC不具备统一的解析解形式,约束条件的存在有两方面影响:一是对于控制量的直接约束;二是基于状态约束反推的间接约束。以指令跟踪为目标,在约束条件未激活的主分区内,分析参数失配的影响,定义在第拍的代价函数为
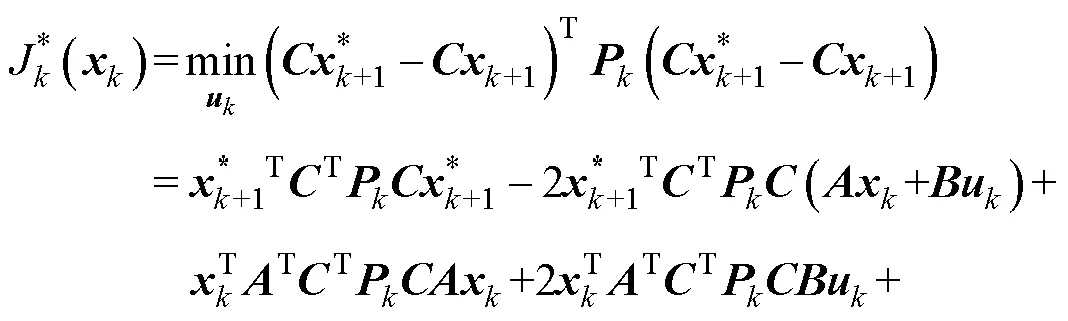
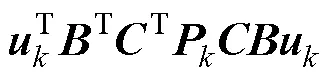
对控制量求梯度为0,得到在拍的无约束最优解为
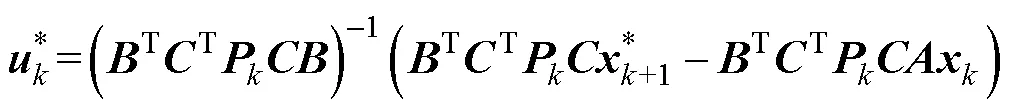

依照式(13)推导的电流控制模型,将式(13)代入式(23),得到电流内环在拍的最优解为
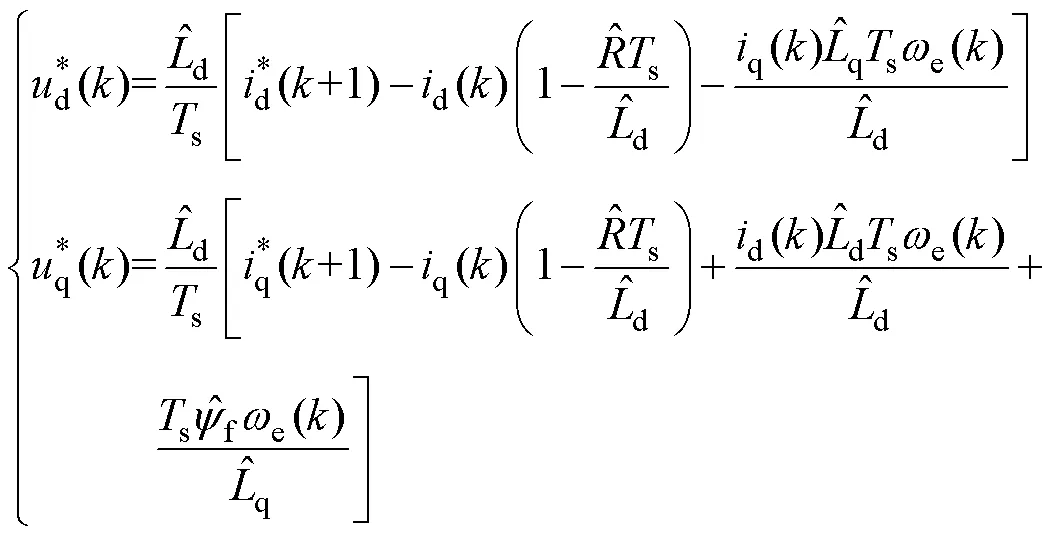
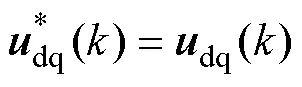
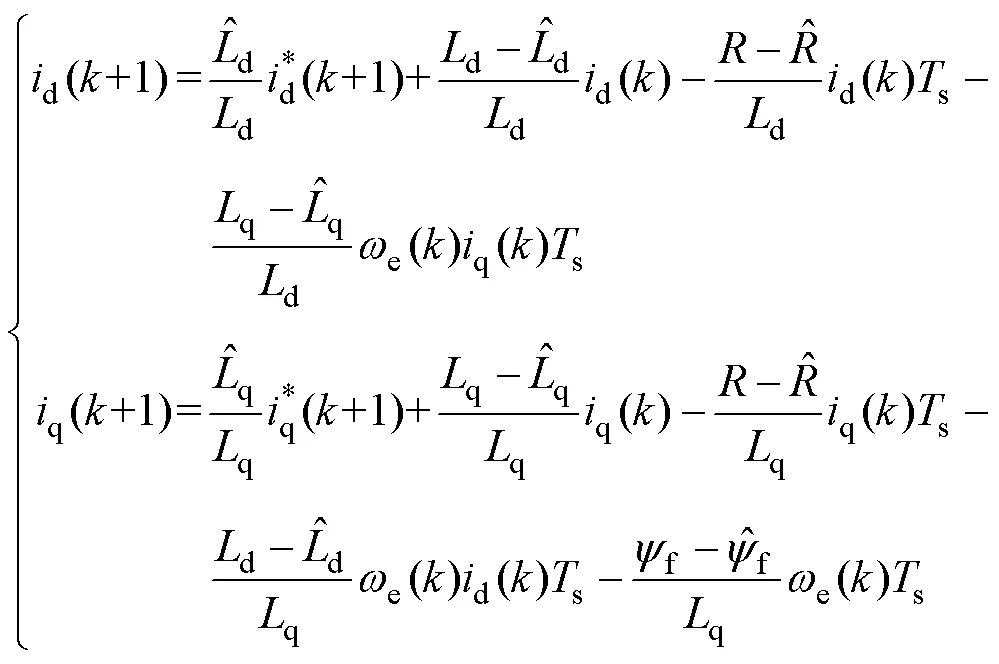
求得+1拍电流误差如式(26)所示,当参数误差皆为0时,电流误差为0。


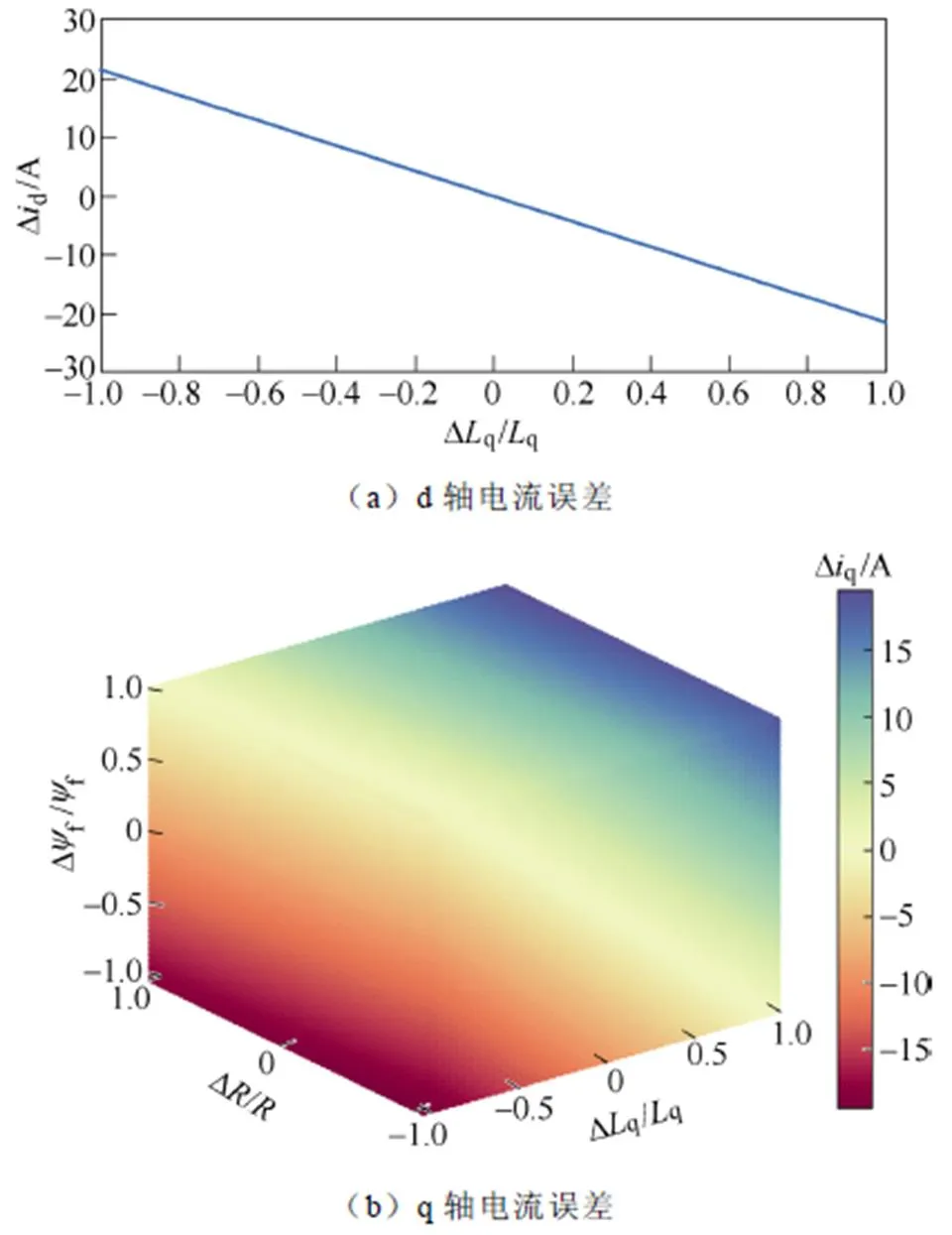
图6 dq轴电流误差示意图
将式(16)代入式(23),转速外环在拍的最优解为
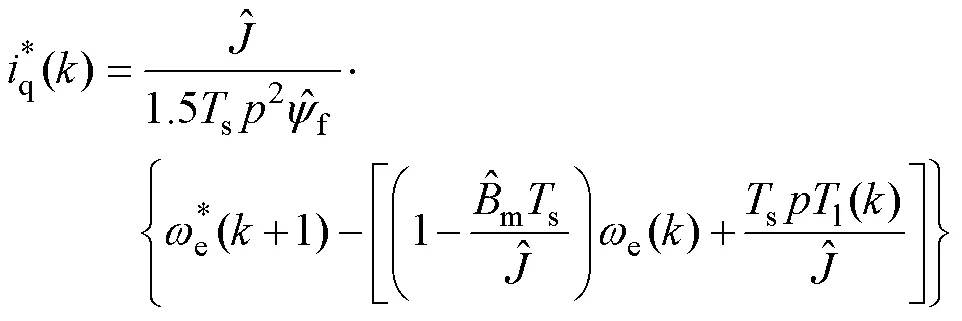
将式(27)代入转速预测方程式(16),+1拍转速为

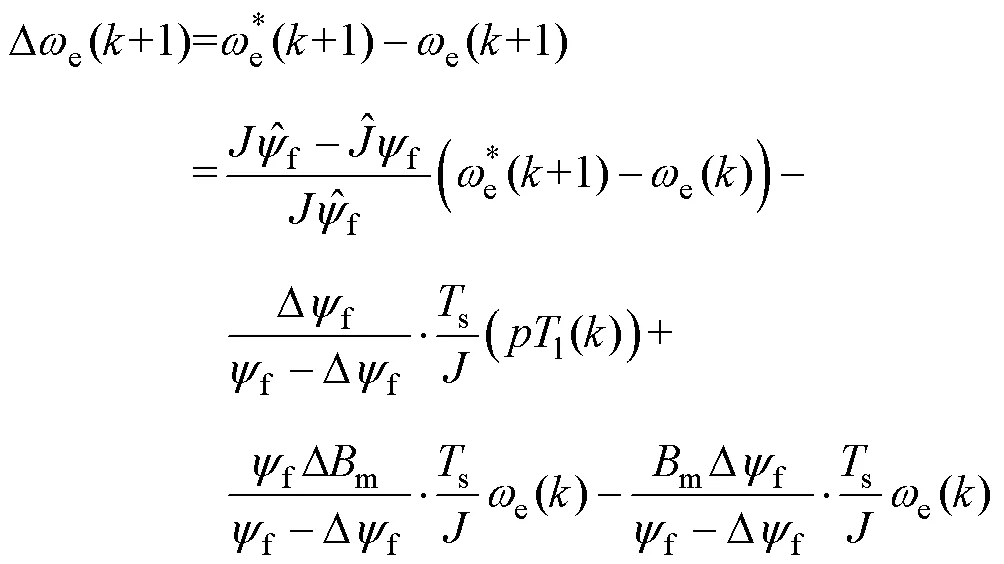
2.4 数字延时
DSP的数字延时特性也属于模型失配范畴,数字控制时序如图8所示,简而言之,即数字延时导致电压指令无法即刻生效,在MPC的应用中将会引起电流振荡甚至失稳[23]。
定义、分别为第拍的真实电压、电流,*()为第拍计算得到的指令电压,()为第拍的采样电流,二者关系为
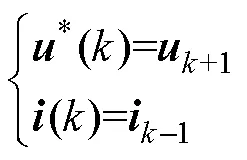
在-1拍计算的电压指令*(-1),在拍下发,记为,经过一拍的作用产生电流,并于+1拍采样,即期望在+1拍采样的电流值到达指令值,需要于-1拍进行计算,于拍下发,有

其中
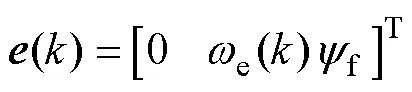
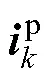

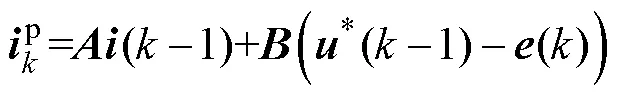
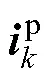
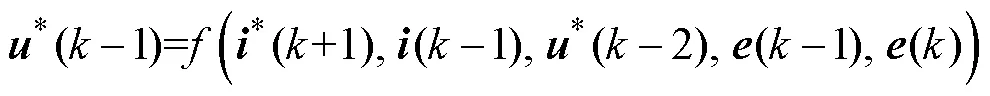
为方便理解,拍待求的最优解*()的表达式为
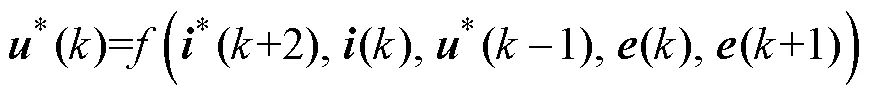

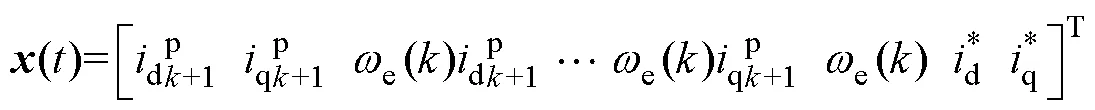
在数字控制中还需要考虑角度延时带来的问题。在FOC策略中,磁场定位的准确性直接影响控制性能,当电压指令作用到电机时,转子已经转过了一定的角度,有
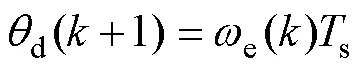
2.5 逆变器非线性
在EMPC应用中,逆变器非线性将带来两方面影响:一是死区电压使得EMPC电压指令与作用到电机的真实电压有区别,产生预测误差,进而导致求解的最优控制量误差[26],由于缺乏对于跟踪误差的校正机制,控制目标将出现偏置误差;二是死区电压将会产生高次电流谐波,引起转矩脉动[27-29]。
考虑逆变器非线性效应的负载对地电压ag为
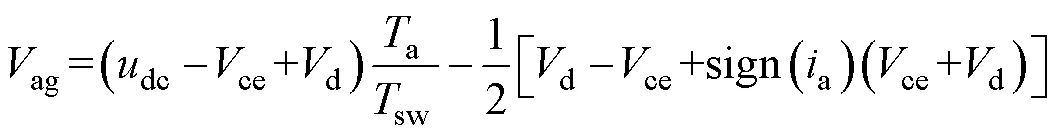
式中,ce、d分别为功率器件管压降及二极管压降;a为A相导通时间;sw为逆变器开关周期;a为A相电流;sign(a)为A相电流符号,定义由逆变器流向负载为正方向。可知,开关周期内的平均电压由导通时间及电流流向决定。
可求得A相电压为
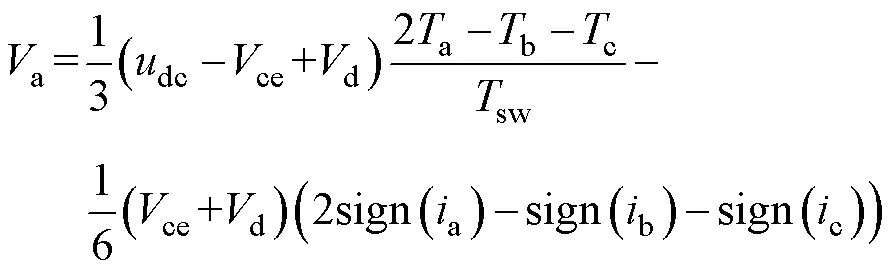
式中,b、c分别为B、C相导通时间。
死区时间内上下桥臂处于关闭状态,负载通过续流二极管被钳位至dc或0,死区效应下有效导通时间为
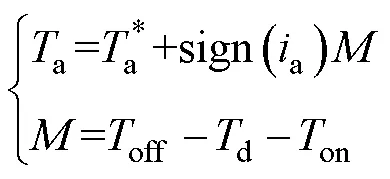
在死区影响下的A相电压为
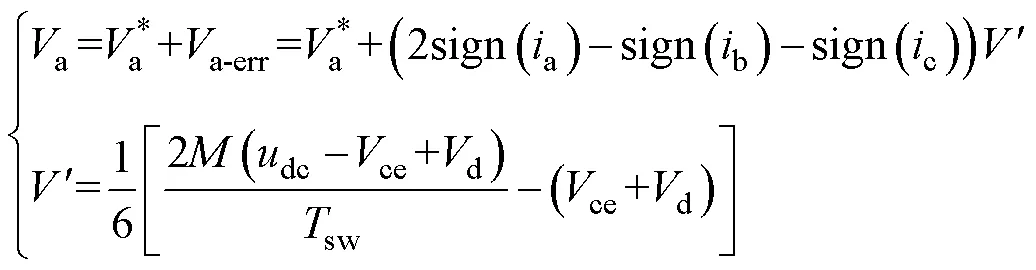
图9 死区失真电压(A相)
Fig.9 Dead zone distortion voltage (phase A)
体现在DSP数字化实现过程中,对EMPC查询得到的最优电压控制量进行电压重构,首先将三相失真电压变换到dq坐标系,有
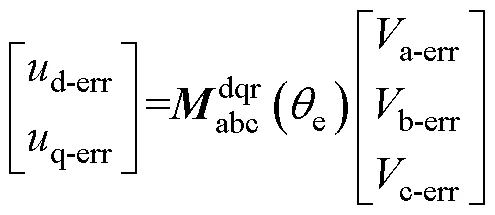

2.6 无静差跟踪
模型失配是MPC算法在应用中的共性问题,包括预测模型之外的扰动及模型内参数失配[30-31],2.3~2.5节皆属于模型失配范畴。由于EMPC的最优控制量只取决于当前状态值,与历史无关,因此无法保证系统实现无静差跟踪,常见的方法是构建扰动模型[32-33]或者在环路中加入积分器[2]。本文构建非线性积分环节为

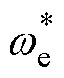
体现在EMPC数字化实现过程中,即在拍进行临界分区查询时将式(36)所示的状态量更新为
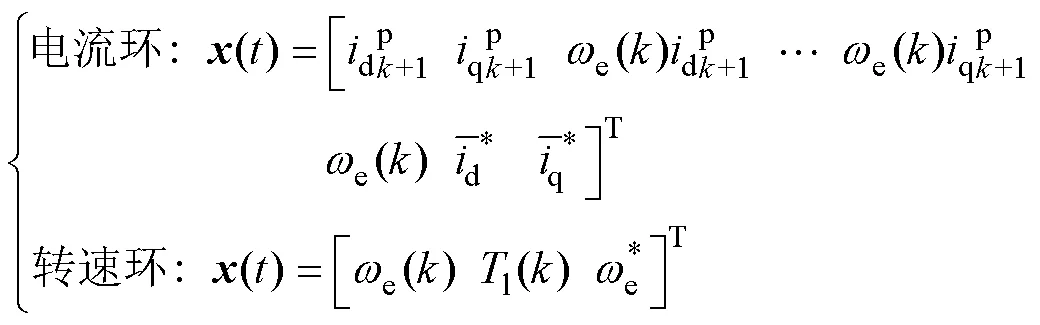
2.7 EMPC实现
基于KKT条件的CFTOC问题离线求解需要进行约束条件与最优解的逻辑判定。随着系统状态量维度的增高,人工求解的难度大大提升,本文使用基于Matlab软件的多参数工具箱(Multi-Parametric Toolbox 3.0)完成问题定义及求解[34]。按照2.1节、2.2节定义的问题及约束条件,定义母线电压约束峰值dc=150 V,电流峰值max=100 A,预测时域=3,算法实现流程如图10所示,左侧为离线部分,展示从系统定义到最优控制律代码生成的过程,并标注了MPT3工具箱相关函数,主要函数用法在本文附录中展示;右侧为在线部分,展示最优控制律查询及相关非理想因素补偿策略。
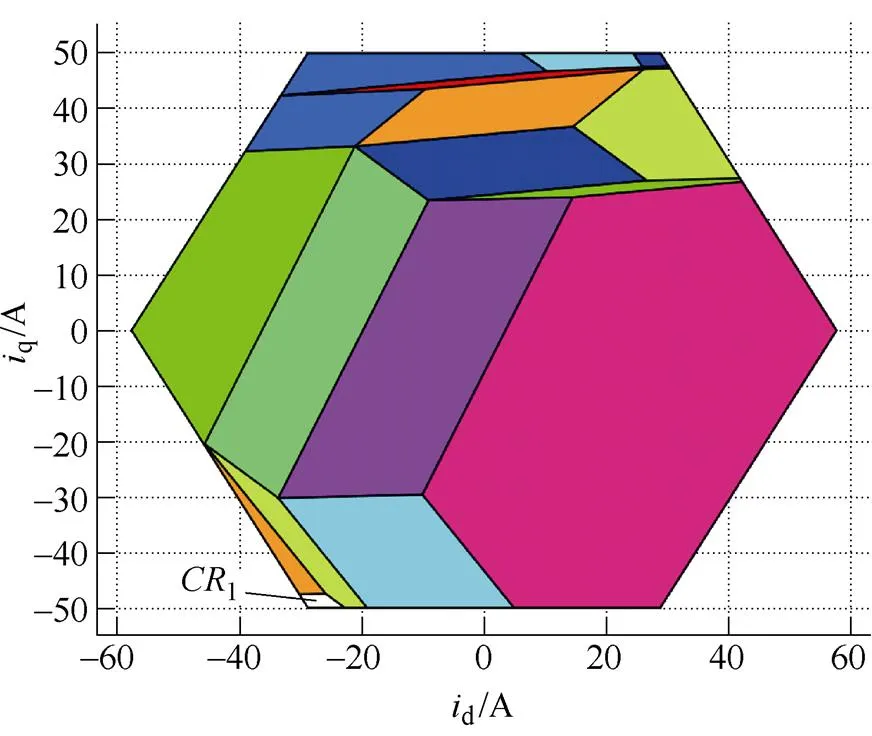
图11 EMPC临界分区-电流控制

图13 EMPC临界分区-转速控制
Fig.13 EMPC critical region-speed control
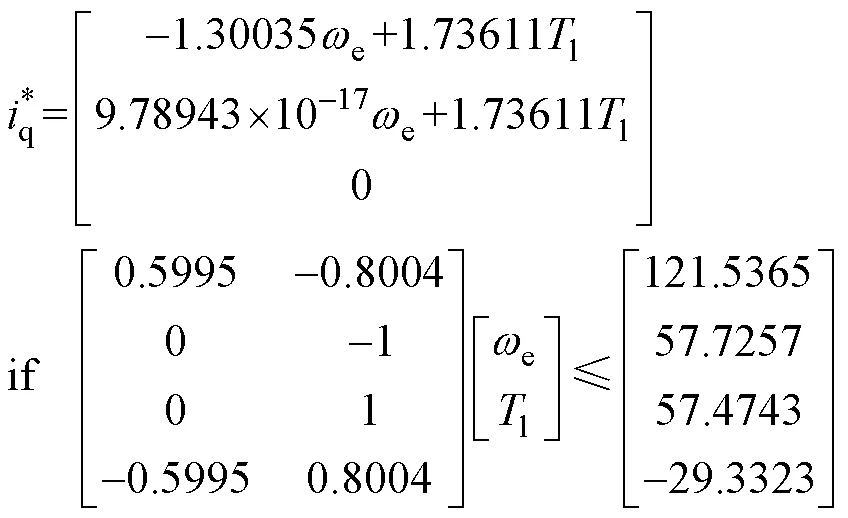
不同分区内的最优代价函数如图14所示,可知除无解分区外,还存在代价函数不等于0的分区,即约束条件的存在使得最优解在预测时域内无法完成跟踪目标。
图14 EMPC临界分区-转速控制
Fig.14 EMPC critical region-speed control
3 仿真验证

3.1 电流控制

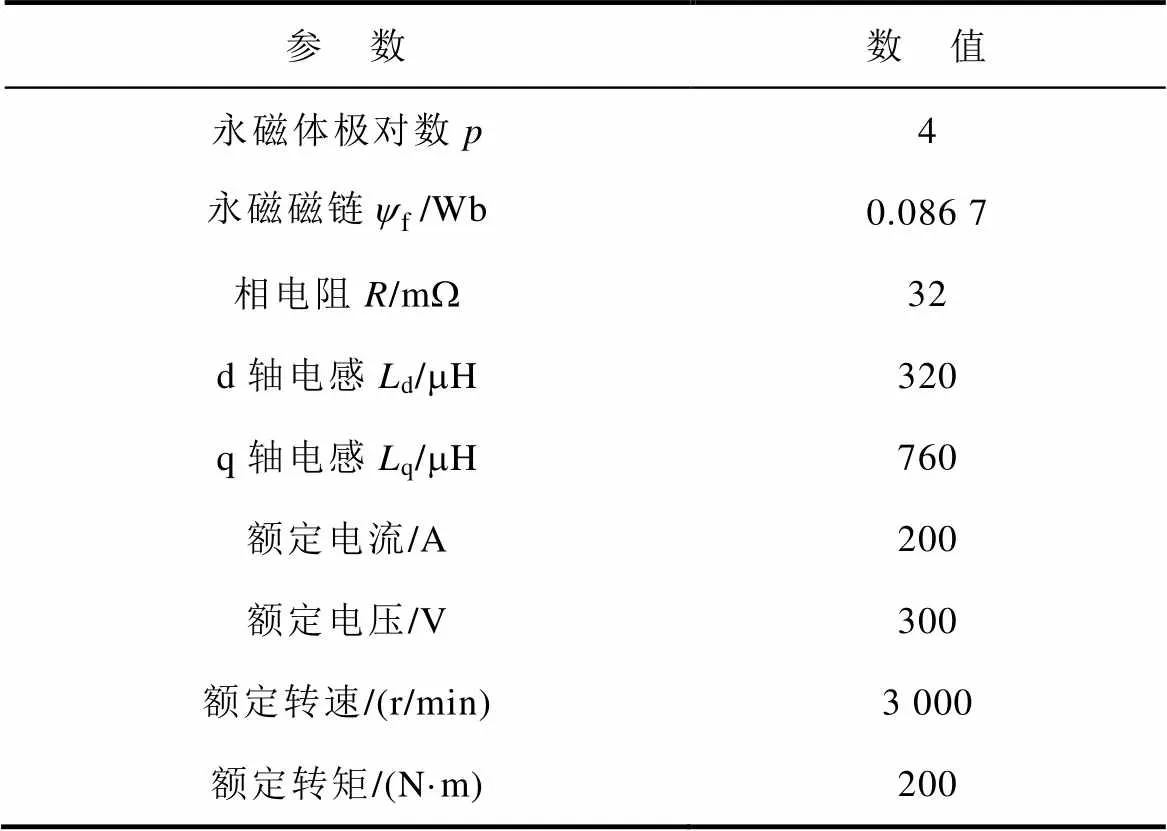
表1 永磁同步电机参数
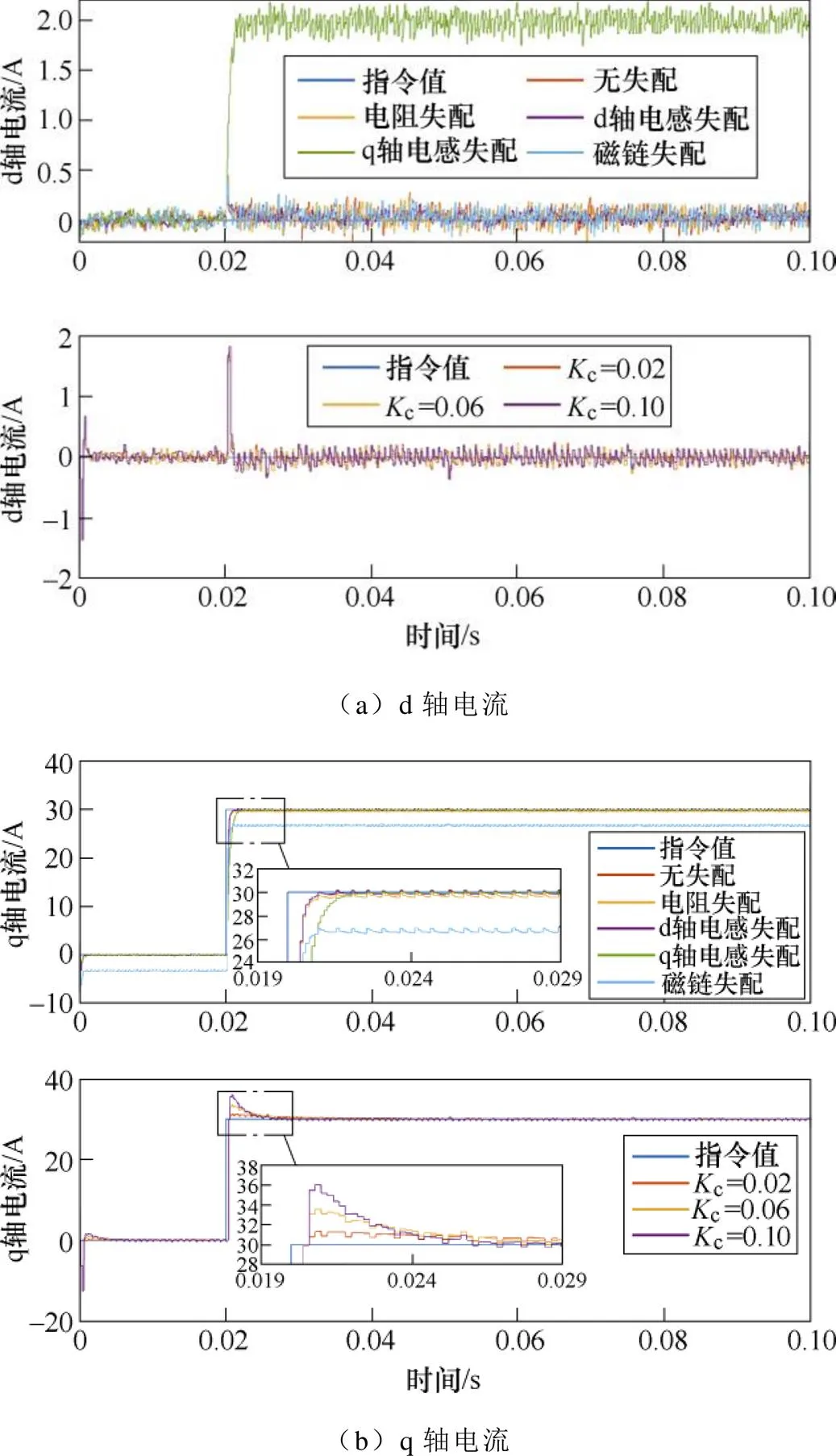
图15 参数失配-电流控制仿真
图16a、图16b为死区影响下的EMPC电流控制效果,图16c为d、q电流快速傅里叶变换(Fast Fourier Transform, FFT)分析,二者皆出现了明显的6次谐波,且q轴电流已经无法完成指令跟踪。基于式(41)~式(43)进行电压重构后有效解决了偏置误差及电流谐波的问题。
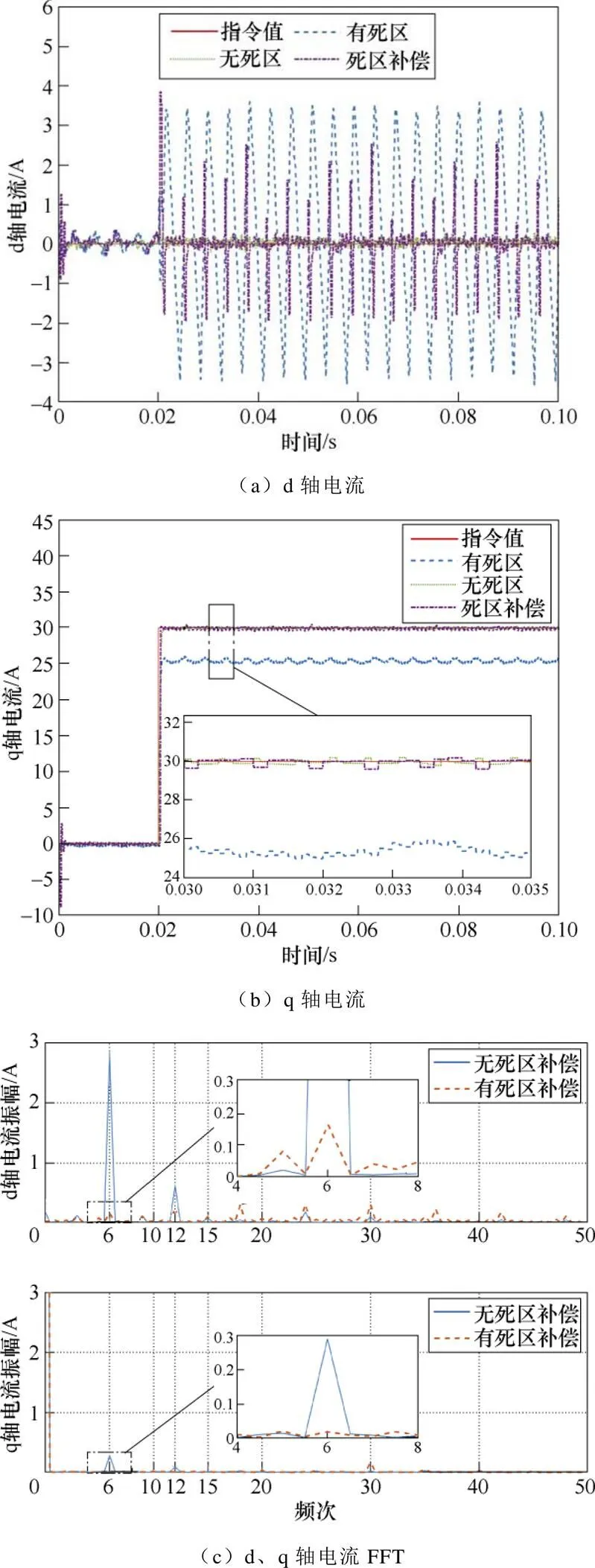
图16 死区效应-电流控制仿真
图17a、图17b展示d、q轴电流由DSP数字延时及角度延时带来的影响,以及基于式(35)~式(37)的补偿效果。如2.4节分析,数字延时将导致大幅电流振荡,角度延时导致FOC磁场定位偏差,在d轴上出现偏置误差。
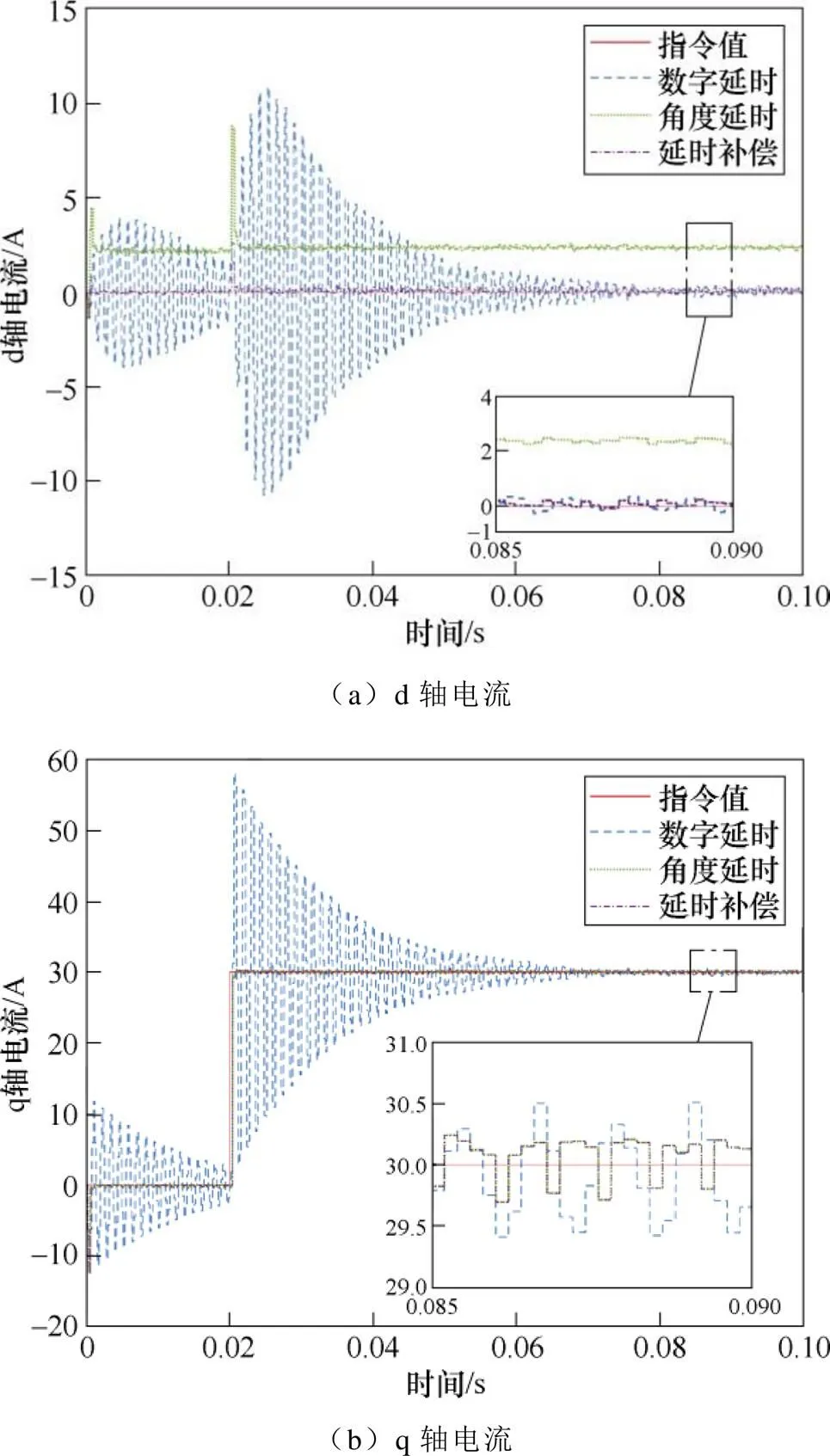
图17 数字延时、角度延时-电流控制仿真
3.2 转速控制
转速控制仿真设定永磁同步电机工作在转矩模式,在0.02 s处给定转速阶跃指令*=600 r/min,0.06 s处给定负载阶跃l=20 N·m。图18展示各项参数失配对于转速控制的影响以及加入非线性积分后的控制效果,结合式(29)分析结果,转速控制稳态精度受磁链参数影响较明显,本文后续实验中选择非线性积分系数s=0.01。图19为转速控制中的死区效应以及死区补偿效果,在未加死区补偿工况下,EMPC转速控制无法完成无静差跟踪。
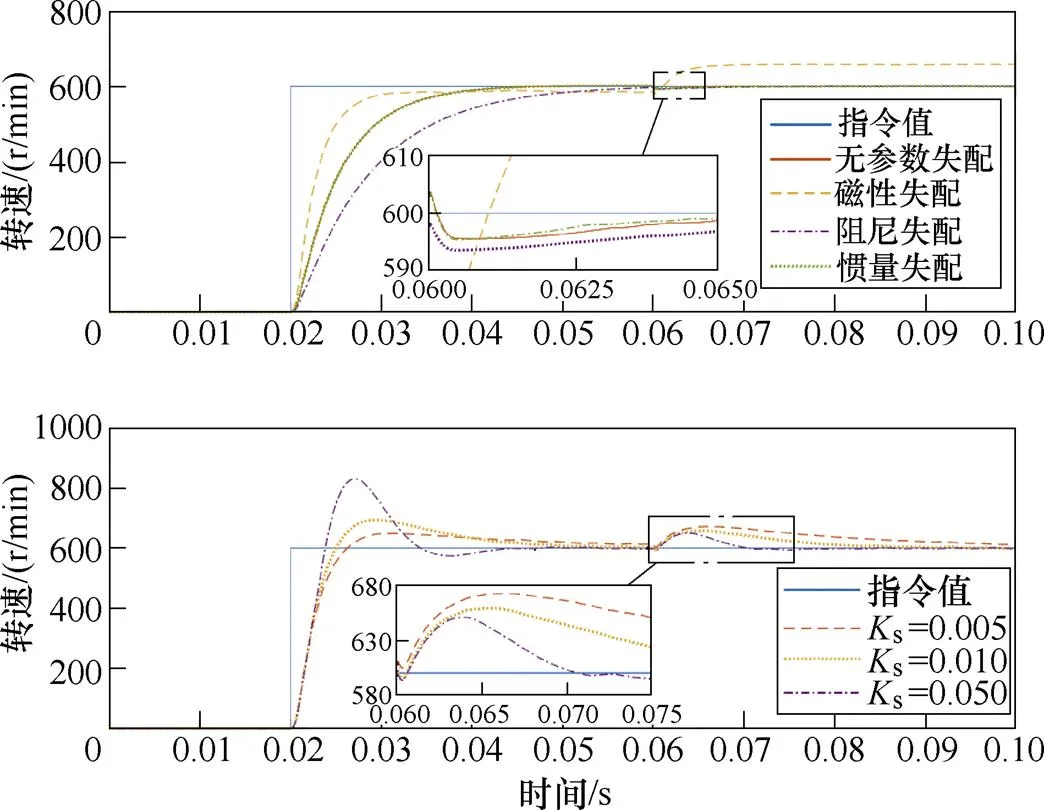
图18 参数失配-转速控制仿真
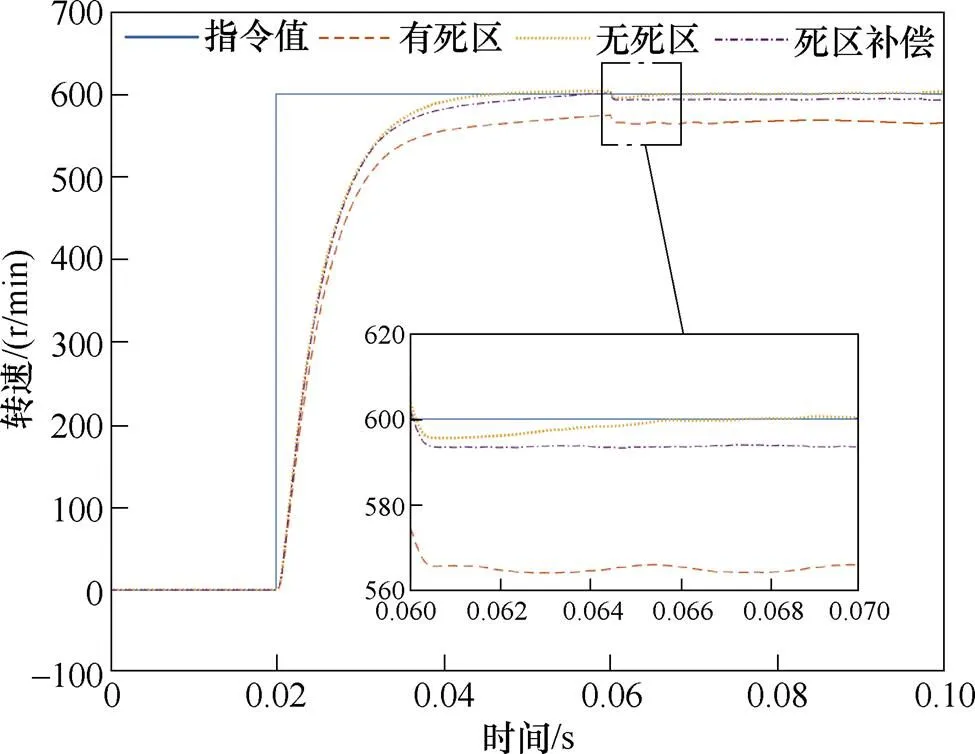
图19 死区效应-转速控制仿真
4 实验验证
搭建了基于TI公司TMS320F2838d作为主控芯片的实验平台,该芯片有两个C28x架构的32位CPU,每个CPU各有44 KB的本机RAM及共享128 KB的全局RAM。EMPC最优控制律转化为C代码后,控制律系数以数组形式保存,芯片内存占用如图20所示,单位为字(2 bytes),共生成以MPT为前缀的8个数组。图20中,以_S为后缀的是转速控制分区数组,无后缀的是电流控制分区数组。其中MPT_ABNC数组用于判定当前状态量是否处于全局状态约束范围内,MPT_HTBFTBGTB数组用于判定当前状态量所处的临界分区编号,MPT_FG数组为该分区内的最优控制律系数。芯片内存占用空间如式(48)所示,转速控制分区数组占用空间1 418×2 bytes,约2.8 KB,电流控制分区数组占用空间13 226×2 bytes,约26.4 KB。逆变器开关频率s=5 kHz,控制周期总时长为200ms,在转速环与电流环查询程序前后分别对GPIO引脚进行置位,通过示波器采集引脚电平得到的程序运行时间如图21所示,转速环程序查询时间为12.364 8ms,电流环程序查询时间为54.110 4ms。
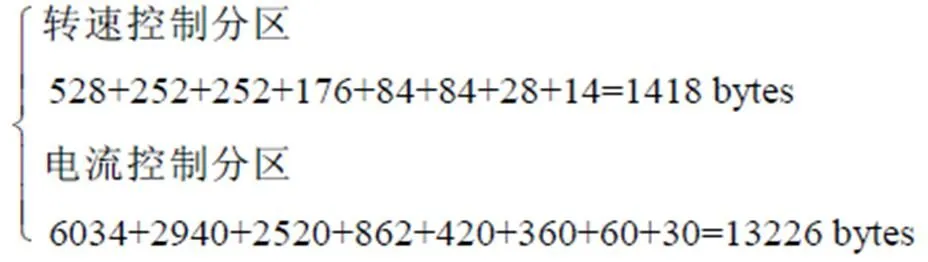
控制器同时驱动两台永磁同步电机同轴共母线运行,共享控制信息,L电机工作在电流环、R电机工作在转速环,A电机工作在电流环、B电机工作在转速环,电机台架及控制器如图22所示。

图22 对拖实验平台
4.1 电流控制
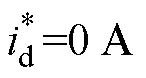

图23 参数失配、死区效应、数字延时-电流控制实验
保留失配参数及死区时间,对各类非理想因素进行补偿后,图24a、图24b展示在相同工况下EMPC与PI两种控制策略的效果对比,图24c展示两种算法的电压指令对比及不同状态下EMPC激活的临界分区。PI控制中由于环路之间的耦合影响,q轴电流加载给d轴电流带来明显的扰动影响,经过0.1 s后回到稳态,q轴电流于0.5 s处加载后,经过0.1 s到达指令值,且伴随着一定的超调;EMPC算法于0.5 s处给定电流指令,指令下发之前,电机处于临界分区7,在指令响应初期电机状态发生变化,切换到临界分区22,该分区内控制电压运行在约束边界,保证最大化的电压利用率,d、q轴电流皆经过7个控制周期到达指令值,用时0.001 4 s,相较PI算法表现出明显的快速性,有效降低耦合效应的同时无超调现象,进入稳态后最优控制电压处于约束内部,切换到临界分区17。需要注意的是,EMPC最优控制律是控制电压与临界分区内状态量的仿射关系,并不指代控制电压量本身,7与17各自指代一组控制律,该分区内对应的最优控制量皆处于约束内部,22分区对应的最优控制量都处于约束边界。图25展示两种算法d、q轴电流FFT分析结果,相较于PI控制,EMPC算法表现出了更好的谐波电流抑制能力。
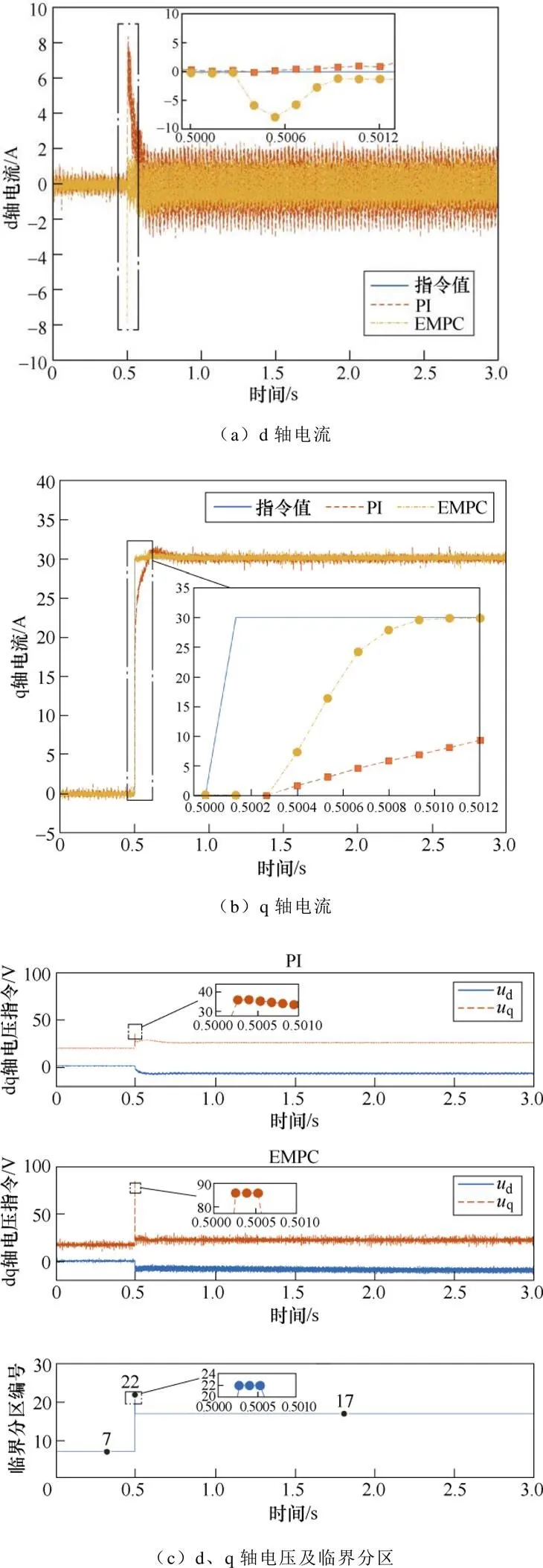
图24 EMPC、PI电流控制实验
4.2 转速控制
转速实验工况与仿真保持一致,给定R电机转速阶跃指令*=600 r/min,图26展示在参数失配及死区效应影响下的转速控制效果,二者都产生了偏置误差,与2.3、2.5、3.2节仿真及理论分析吻合。
对非理想因素进行补偿后,图27a展示EMPC与PI两种控制策略的效果对比,于0.5 s处给定转速指令,PI算法经过1 s到达稳态,伴随着较为明显的超调现象;EMPC算法经过0.3 s到达指令值且无超调现象。转速环的最优控制量为电流环q轴电流指令,图27b展示动态过程中两种算法的q轴电流指令对比及EMPC临界分区切换情况,转速环模型不存在如电流环模型d、q轴的状态耦合。PI控制在指令跟踪初期也可以响应最大约束电流,但是由于机械环节响应速度较慢,基于误差调节的方式无法快速找到最优解,仍然有超调现象存在。EMPC算法在动态响应过程中最优控制量到达约束边界,临界分区由9切换到15,进入稳态后控制量回到约束内部,切换到12。图27c展示电流内环控制电压指令。4.1节对EMPC电流控制分析完毕,此处不再展开。
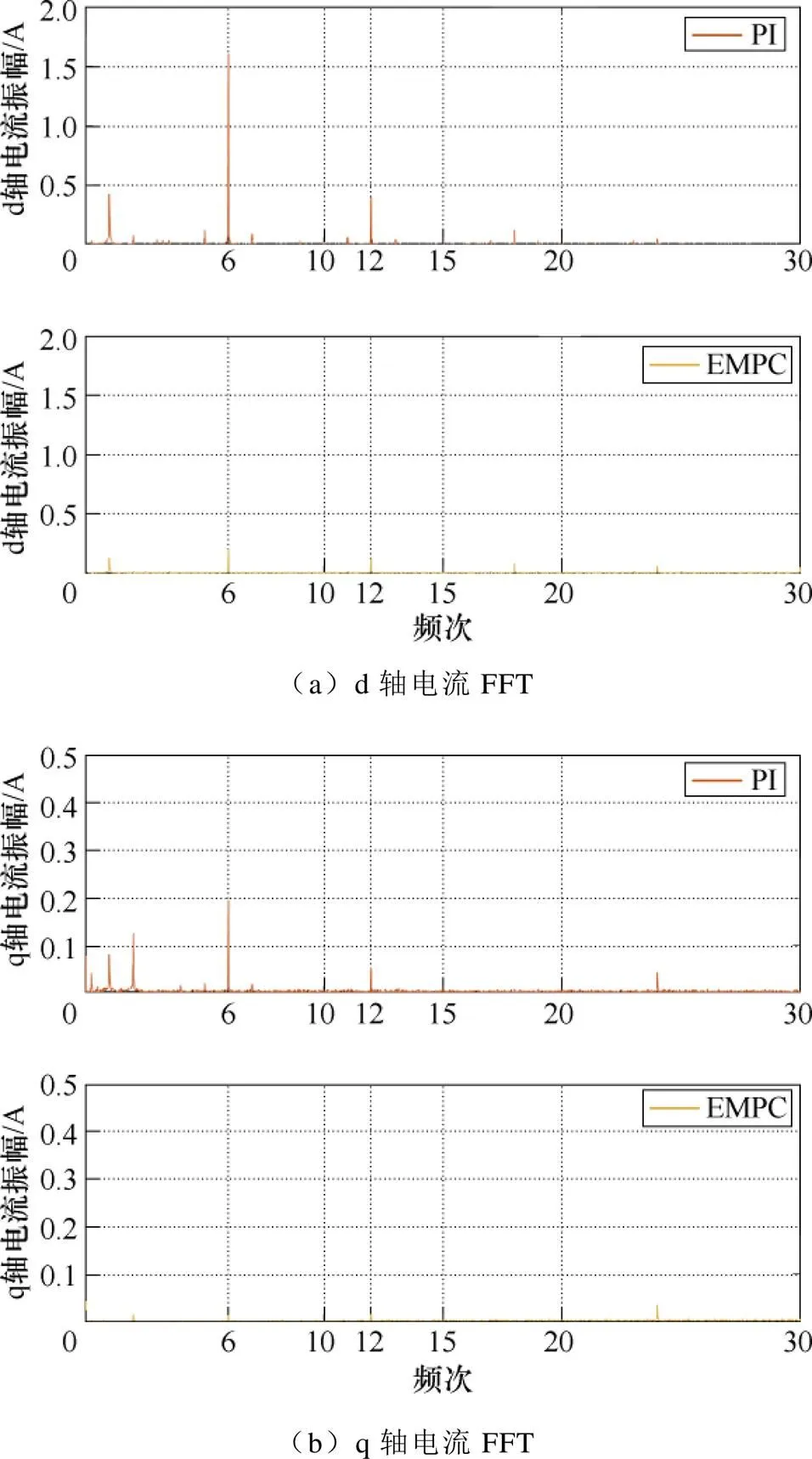
图25 EMPC、PI FFT-电流控制实验
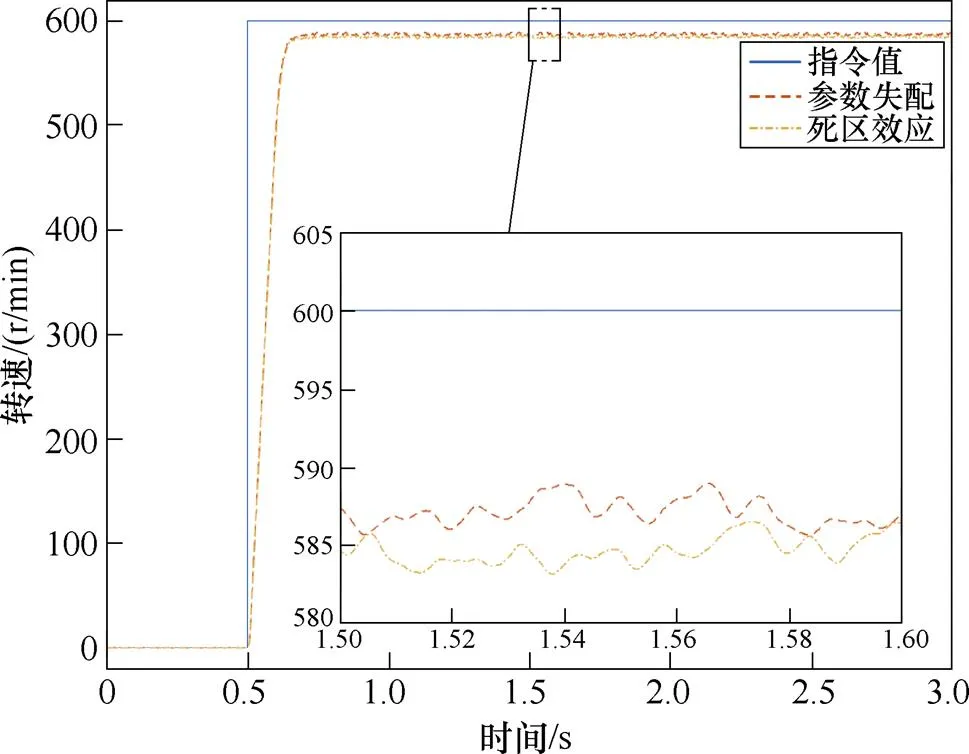
图26 参数失配、死区效应-转速控制实验

图27 EMPC、PI-转速控制实验
保持相同的控制参数,R电机进入稳态后,由L电机给定30 A电流负载,图28a为PI与EMPC两种算法在突加负载时的转速数据对比。PI控制最大超调量65 r/min,经过0.5 s回到稳态;EMPC算法最大超调量6 r/min,经过0.1 s回到稳态,电流动态响应更为平滑。图28b展示两种算法q轴电流指令对比及EMPC临界分区,EMPC电流指令平滑无振荡,保证了在扰动下对于转速指令的快速响应,该工况下临界分区保持在12,最优控制律未发生变化,图28c展示电流内环控制电压指令。
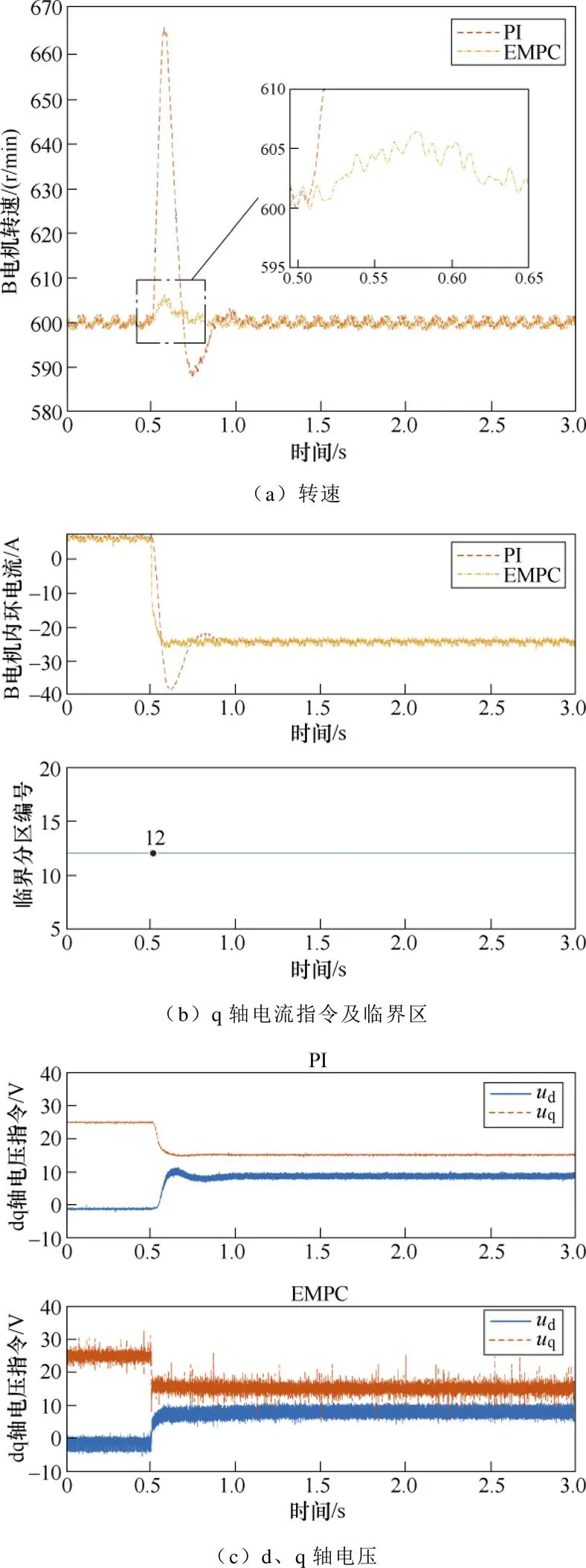
图28 EMPC、PI-转速控制实验
5 结论
本文针对高性能永磁同步电机控制提出一种级联式EMPC算法,以电流及转速跟踪目标为代价函数,通过离线求解有约束问题的最优解,以分段仿射函数的显式表达存储于多面体临界分区中,解决了传统MPC在线求解算力消耗大的问题。基于多参数规划思想完成系统线性化建模,消除了电机系统环路之间的耦合项及非线性转速项带来的扰动。在模型中加入非线性积分环节,普适性地解决了各类模型失配带来的影响。通过仿真及实验验证了算法的有效性及优越性,得到以下结论:
1)相较于抗饱和策略只能应用于一些特定工作点,并可能导致系统的不稳定,EMPC算法将模型及各类约束条件纳入控制问题的求解,包含了控制过程中所有的动态特征,保证系统线性稳定的同时得到了更好的动态性能。
2)相较于PI控制,EMPC算法的高带宽特性使其具有更快的动态响应速度及谐波抑制能力;基于多变量控制思想的设计方法使其不再需要考虑系统状态之间的耦合作用;基于可行域求解的最优控制量可以满足全域的控制需求,不再需要根据工况进行繁琐的调参工作。
附录 MPT3工具箱函数介绍
MPT3工具箱网址:http://www.tbxmanager.com/
1. Model=LTISystem (‘A’, A, ‘B’, B, ‘C’, C, ‘D’, D, ‘T_s ’, Ts):系统定义函数,定义线性时不变系统,ABCD矩阵定义如2.1节及表1所示。
2. Ctrl=MPCController (model, horizon):控制器函数,基于线性时不变系统定义,horizon为预测时域。
3. Px/Pu=Polyhedron (‘A’, A, ‘b’, b):多面体函数,定义约束多面体,{|≤}。
4. x/u.setConstraint ( ):对状态量及控制量分别设置控制器约束。
5. y.reference ( ):设置输出参考指令。
6. y.penalty ( ):设置输出惩罚系数。
7. Ectrl=model.toExplicit:将控制器转化为显式MPC。
8. Ectrl.exportToC:将最优控制律转化为C代码。
[1] Cui Kai, Wang Chenchen, Gou Lifeng, et al. Analysis and design of current regulators for PMSM drives based on DRGA[J]. IEEE Transactions on Trans- portation Electrification, 2020, 6(2): 659-667.
[2] Belda K, Vošmik D. Explicit generalized predictive control of speed and position of PMSM drives[J]. IEEE Transactions on Industrial Electronics, 2016, 63(6): 3889-3896.
[3] Mariethoz S, Domahidi A, Morari M. High-bandwidth explicit model predictive control of electrical drives[J]. IEEE Transactions on Industry Applications, 2012, 48(6): 1980-1992.
[4] De Doná J A, Goodwin G C, Seron M M. Anti-windup and model predictive control: reflections and con- nections[J]. European Journal of Control, 2000, 6(5): 467-477.
[5] Richalet J, Rault A, Testud J L, et al. Model algorithmic control of industrial processes[J]. IFAC Proceedings Volumes, 1977, 10(16): 103-120.
[6] Richalet J, Rault A, Testud J L, et al. Model predi- ctive heuristic control[J]. Automatica, 1978, 14(5): 413-428.
[7] Clarke D W, Mohtadi C, Tuffs P S. Generalized predictive control-part I. the basic algorithm[J]. Automatica, 1987, 23(2): 137-148.
[8] Clarke D W, Mohtadi C, Tuffs P S. Generalized predictive control-part II extensions and inter- pretations[J]. Automatica, 1987, 23(2): 149-160.
[9] Rodriguez J, Cortes P. Predictive control of power converters and electrical drives[M]. Chichester, West Sussex, UK: John Wiley & Sons, 2012.
[10] Karamanakos P, Liegmann E, Geyer T, et al. Model predictive control of power electronic systems: methods, results, and challenges[J]. IEEE Open Journal of Industry Applications, 2020, 1: 95-114.
[11] Zhang Yongchang, Xie Wei, Li Zhengxi, et al. Low-complexity model predictive power control: double-vector-based approach[J]. IEEE Transactions on Industrial Electronics, 2014, 61(11): 5871-5880.
[12] Zhang Yongchang, Xie Wei. Low complexity model predictive control-single vector-based approach[J]. IEEE Transactions on Power Electronics, 2014, 29(10): 5532-5541.
[13] 陈荣, 翟凯淼, 舒胡平. 永磁同步电机双矢量固定开关频率模型预测控制研究[J]. 电工技术学报, 2023, 38(14): 3812-3823.
Chen Rong, Zhai Kaimiao, Shu Huping. Predictive control of dual vector fixed switching frequency model for permanent magnet synchronous motor[J]. Transactions of China Electrotechnical Society, 2023, 38(14): 3812-3823.
[14] 李祥林, 薛志伟, 阎学雨, 等. 基于电压矢量快速筛选的永磁同步电机三矢量模型预测转矩控制[J]. 电工技术学报, 2022, 37(7): 1666-1678.
Li Xianglin, Xue Zhiwei, Yan Xueyu, et al. Voltage vector rapid screening-based three-vector model predictive torque control for permanent magnet syn- chronous motor[J]. Transactions of China Elec- trotechnical Society, 2022, 37(7): 1666-1678.
[15] 张珍睿, 刘彦呈, 陈九霖, 等. 永磁同步电机幅值控制集模型预测控制策略[J]. 电工技术学报, 2022, 37(23): 6126-6134.
Zhang Zhenrui, Liu Yancheng, Chen Jiulin, et al. Amplitude control set model predictive control strategy for permanent magnet synchronous motor[J]. Transactions of China Electrotechnical Society, 2022, 37(23): 6126-6134.
[16] 郑长明, 阳佳峰, 高昂, 等. 永磁同步电机长线变频驱动系统定频滑模预测电流控制[J]. 电工技术学报, 2023, 38(4): 915-924.
Zheng Changming, Yang Jiafeng, Gao Ang, et al. Fixed switching frequency sliding-mode predictive current control of a PMSM variable-frequency drive system with long cables[J]. Transactions of China Electrotechnical Society, 2023, 38(4): 915-924.
[17] 周奇勋, 刘帆, 吴紫辉, 等. 永磁同步电机转矩与定子磁链模型预测控制预测误差补偿方法[J]. 电工技术学报, 2022, 37(22): 5728-5739.
Zhou Qixun, Liu Fan, Wu Zihui, et al. Model predictive torque and stator flux control method for PMSMs with prediction error compensation[J]. Transactions of China Electrotechnical Society, 2022, 37(22): 5728-5739.
[18] Geyer T, Quevedo D E. Performance of multistep finite control set model predictive control for power electronics[J]. IEEE Transactions on Power Elec- tronics, 2015, 30(3): 1633-1644.
[19] Scoltock J, Geyer T, Madawala U K. A comparison of model predictive control schemes for MV induction motor drives[J]. IEEE Transactions on Industrial Informatics, 2013, 9(2): 909-919.
[20] Borrelli F, Bemporad A, Morari M. Predictive control for linear and hybrid systems[M]. New York: Cambridge University Press, 2017.
[21] Bemporad A, Morari M, Dua V, et al. The explicit linear quadratic regulator for constrained systems[J]. Automatica, 2002, 38(1): 3-20.
[22] Boyd S, Vandenberghe L. Convex optimization[M]. Cambridge, UK: Cambridge University Press, 2004.
[23] Springob L, Holtz J. High-bandwidth current control for torque-ripple compensation in PM synchronous machines[J]. IEEE Transactions on Industrial Elec- tronics, 1998, 45(5): 713-721.
[24] Abdel-Rady I M Y, El-Saadany E F. An improved deadbeat current control scheme with a novel adaptive self-tuning load model for a three-phase PWM voltage-source inverter[J]. IEEE Transactions on Industrial Electronics, 2007, 54(2): 747-759.
[25] 国敬, 范涛, 章回炫, 等. 高速低载波比下永磁同步电机电流环稳定性分析[J]. 中国电机工程学报, 2019, 39(24): 7336-7346, 7506.
Guo Jing, Fan Tao, Zhang Huixuan, et al. Stability analysis of permanent magnet synchronous motor current loop control at high speed and low carrier ratio[J]. Proceedings of the CSEE, 2019, 39(24): 7336-7346, 7506.
[26] Chen Jiahao, Mei Jie, Yuan Xin, et al. Online adapta- tion of two-parameter inverter model in sensorless motor drives[J]. IEEE Transactions on Industrial Electronics, 2022, 69(10): 9860-9871.
[27] Choi J W, Sul S K. Inverter output voltage synthesis using novel dead time compensation[J]. IEEE Transa- ctions on Power Electronics, 1996, 11(2): 221-227.
[28] Park Y, Sul S K. A novel method utilizing trapezoidal voltage to compensate for inverter nonlinearity[J]. IEEE Transactions on Power Electronics, 2012, 27(12): 4837-4846.
[29] Hwang S H, Kim J M. Dead time compensation method for voltage-fed PWM inverter[J]. IEEE Transa- ctions on Energy Conversion, 2010, 25(1): 1-10.
[30] Young H A, Perez M A, Rodriguez J. Analysis of finite-control-set model predictive current control with model parameter mismatch in a three-phase inverter[J]. IEEE Transactions on Industrial Elec- tronics, 2016, 63(5): 3100-3107.
[31] Wipasuramonton P, Zhu Z Q, Howe D. Predictive current control with current-error correction for PM brushless AC drives[J]. IEEE Transactions on Industry Applications, 2006, 42(4): 1071-1079.
[32] Muske K R, Badgwell T A. Disturbance modeling for offset-free linear model predictive control[J]. Journal of Process Control, 2002, 12(5): 617-632.
[33] Faanes A, Skogestad S. Offset-free tracking of model predictive control with model mismatch: experi- mental results[J]. Industrial & Engineering Chemistry Research, 2005, 44(11): 3966-3972.
[34] Herceg M, Kvasnica M, Jones C N, et al. Multi- parametric toolbox 3.0[C]//2013 European Control Conference (ECC), Zurich, Switzerland, 2013: 502-510.
Research on High-Performance Explicit Model Predictive Control Algorithm for Permanent Magnet Synchronous Motors
1,21,221,2
(1. University of Chinese Academy of Sciences Beijing 100049 China 2. Institute of Electrical Engineering Chinese Academy of Sciences Beijing 100190 China)
Since the 1970s, model predictive control (MPC) algorithms have proven to be effective control strategies for multi-input and multi-output nonlinear dynamic systems with complex constraints. However, due to the significant computational demands associated with optimization problems, applying MPC to control objects with fast response time requirements, such as motor systems, presents challenges in achieving iterative solutions for constrained problems within short control cycles. This paper proposes a high-performance control strategy for permanent magnet synchronous motors based on the explicit model predictive control (EMPC) concept. The strategy involves the establishment of linearized models for current and speed control using multiparametric programming to eliminate coupling effects and nonlinear influences between states. The offline solution yields optimal control actions under effective constraint conditions, stored as piecewise-affine functions. During operation, the corresponding optimal control actions are obtained by querying the partition containing the current state combination. The paper comprehensively analyzes model mismatch, digital delay, and dead-zone effects in EMPC applications and provides corresponding solutions. A fully automated dyno test platform verifies the proposed algorithm's efficacy.
The paper introduces the theoretical foundations of multiparametric programming and presents a comprehensive design process for explicit model predictive control. It establishes linearized models for controlling current and speed in permanent magnet synchronous motors while linearizing voltage and current constraints. The effects of parameter mismatch, digital delay, and inverter nonlinearity on EMPC are analyzed, and respective compensatory measures are proposed. The EMPC problem definition and optimal control law are solved using the MPT3 toolbox, displaying critical partitions and optimal cost functions under different state combinations. The simulation verifies the algorithm and the preceding analysis of various non-ideal factors. Experimental validation is conducted on a motor dyno test platform, comparing the performance of EMPC with a proportional-integral (PI) control algorithm. In the current control scenario, when given a 30 A current step command, the PI algorithm exhibits a response time of 0.1 s, while the EMPC algorithm responds in 0.001 4 s. In speed control, with a 600 r/min speed step command, the PI algorithm takes 1 s to respond, whereas the EMPC algorithm responds in 0.3 s. When subjected to load disturbances, the PI algorithm reaches a steady state after 0.5 s, while the EMPC algorithm reaches a steady state after 0.1 s. The experimental results demonstrate that EMPC effectively reduces coupling effects without overshooting because each control is optimized under constraints, exhibiting superior harmonic current suppression capabilities.
Based on the theoretical analysis and experimental results, the following conclusions can be drawn:
(1) The EMPC algorithm incorporates models and various constraints into the control problem, which can encompass all dynamic characteristics during the control process, guarantee linear stability, and achieve better dynamic performance compared to anti-saturation strategies.
(2) Due to the high bandwidth characteristic, the EMPC algorithm has faster dynamic response and harmonic suppression than PI control. The design approach based on multivariable control does not consider coupling effects between system states, and the optimal control action obtained through feasible region-solving meets global control requirements. Thus, it eliminates the need for cumbersome tuning based on operating conditions.
Permanent magnet synchronous motor (PMSM), explicit model predictive control, optimal control, speed prediction control, current prediction control
刘忠永 男,1995年生,博士研究生,研究方向为永磁同步电机控制、模型预测控制等。E-mail: lzy@mail.iee.ac.cn
范 涛 男,1981年生,研究员,博士生导师,研究方向为永磁电机分析与优化设计、先进电机控制、高性能电力电子装备电子系统设计开发等。E-mail: fantao@mail.iee.ac.cn(通信作者)
TM341
10.19595/j.cnki.1000-6753.tces.230547
国家重点研发计划资助项目(2021YFB2500600)。
2023-04-27
2023-06-07
(编辑 崔文静)

