考虑锚索松弛的悬浮隧道冲击动力响应数值模拟

杨 赢, 雷 岚, 赵 超, 项贻强

(1. 绍兴文理学院土木工程学院, 浙江 绍兴 312000; 2. 浙江交工集团股份有限公司, 浙江 杭州 310051; 3. 浙江大学建筑工程学院, 浙江 杭州 310058)

0 引言

悬浮隧道(submerged floating tunnel,简称SFT)是一种新型交通建筑物,由悬浮在水中一定深度的管体、锚泊系统和与两岸相连的构筑物组成。与传统桥梁相比,悬浮隧道的建设与运营对环境影响较小。此外,悬浮隧道每单位长度的建造成本不随总跨度的增加而增加,为复杂水域的通道建设提供了一种全新的选择[1-2]。在运营过程中,悬浮隧道面临着沉船、坠物、车辆撞击的风险,对隧道结构安全构成极大威胁。

目前,已有学者对悬浮隧道在冲击荷载作用下的动力行为展开了研究。在整体动力响应方面,Xiang等[3]将悬浮隧道管体简化为弹性地基梁,基于Hamilton原理推导了冲击荷载作用下管体的振动控制方程,对管体空间动力响应进行了分析;张嫄等[4]采用弹性支撑梁,通过伽辽金法求解控制方程,分析了在冲击荷载作用下悬浮隧道跨中的时程位移,并讨论了张力腿竖向刚度、冲击物质量、冲击速度对悬浮隧道跨中位移的影响;杨赢等[5]通过ABAQUS中UAMP子程序接口计算管体运动过程中的流体阻力,对冲击荷载作用下悬浮隧道的整体动力响应进行数值模拟,并通过试验验证了建模方法的有效性;Wang等[6]研究了端部约束、管长、结构阻尼和水力阻力等多种因素对冲击载荷作用下悬浮隧道响应的影响,指出当无量纲长度超过100时,端部约束对管体最大位移的影响可以忽略不计。冲击荷载会对管体局部造成损伤,在局部响应方面,杨赢等[7]建立了管体三维实体模型,分析了钢筋混凝土截面和钢-混组合截面在碰撞作用下的损伤情况;Luo等[8]考虑了流固耦合效应,采用SPH法对悬浮隧道管体在遭受潜艇碰撞时的局部动力响应进行了数值模拟。

已有研究表明,锚索式悬浮隧道在极端荷载作用下会出现锚索松弛,对结构安全产生影响。Mazzolani等[9]发现在地震荷载作用下,悬浮隧道锚索会完全失去其初始张力而出现松弛,并表现出明显的非线性行为;Lu等[10-11]通过改变锚索支撑刚度,研究了波浪环境中悬浮隧道的动力学响应,发现在较大的浪高下,锚索易出现松弛现象;苏志彬等[12]考虑了锚索松弛效应,分析了在索端参数激励作用下水中悬浮隧道的振动响应,指出悬浮隧道锚索松弛对其振动的影响不可忽略;Wu等[13]设计了一种水下振动装置来模拟地震激励,研究发现在地震荷载作用下,锚索会产生交替的松弛-张紧行为。锚索一旦发生松弛,其对管体的支撑作用消失,从而影响结构的整体稳定;当再次张紧时,锚索拉力会显著增大,可能导致断索的发生。Xiang等[14-15]研究了锚索突然失效时悬浮隧道的整体动力响应,研究表明锚索突然断裂后,管体振动强烈;阳帅等[16]研究了波流作用下悬浮隧道局部锚索的破断动力响应,得出锚索破断会引起结构的高频振动和产生冲击效应;Wu等[17]的研究指出,不同情况下结构的瞬态效应、力的再分配和冲击力是决定锚索断裂下悬浮隧道失稳和逐渐坍塌的关键因素。冲击荷载量值大,属于极端的荷载工况,也可能导致悬浮隧道锚索出现松弛,对结构安全不利。因此,有必要建立反映真实情况的计算模型,分析冲击荷载作用下考虑锚索松弛效应的动力响应。

本文采用ABAQUS软件建立悬浮隧道在冲击荷载作用下的有限元模型,采用Morison方程计算流体阻力,并通过UAMP子程序进行模拟,分析并对比考虑与不考虑锚索松弛效应下悬浮隧道结构的动力响应,并对冲击荷载、浮重比、锚索倾角等参数对悬浮隧道锚索松弛行为的影响进行研究。

1 悬浮隧道有限元建模

1.1 结构基本参数

悬浮隧道结构示意如图1所示。由于目前还尚未有悬浮隧道建成的先例,因此,本文计算参数取自文献[5]和文献[18],如表1所示。悬浮隧道管体的总长度为2 000 m,沿管体轴线方向均匀布置19对锚索。为简化计算过程,假定各根锚索具有相同的物理参数。因管体冗余浮力的作用,锚索处于张紧状态。不考虑管段接头和碰撞局部损伤对管体整体抗弯刚度的影响。

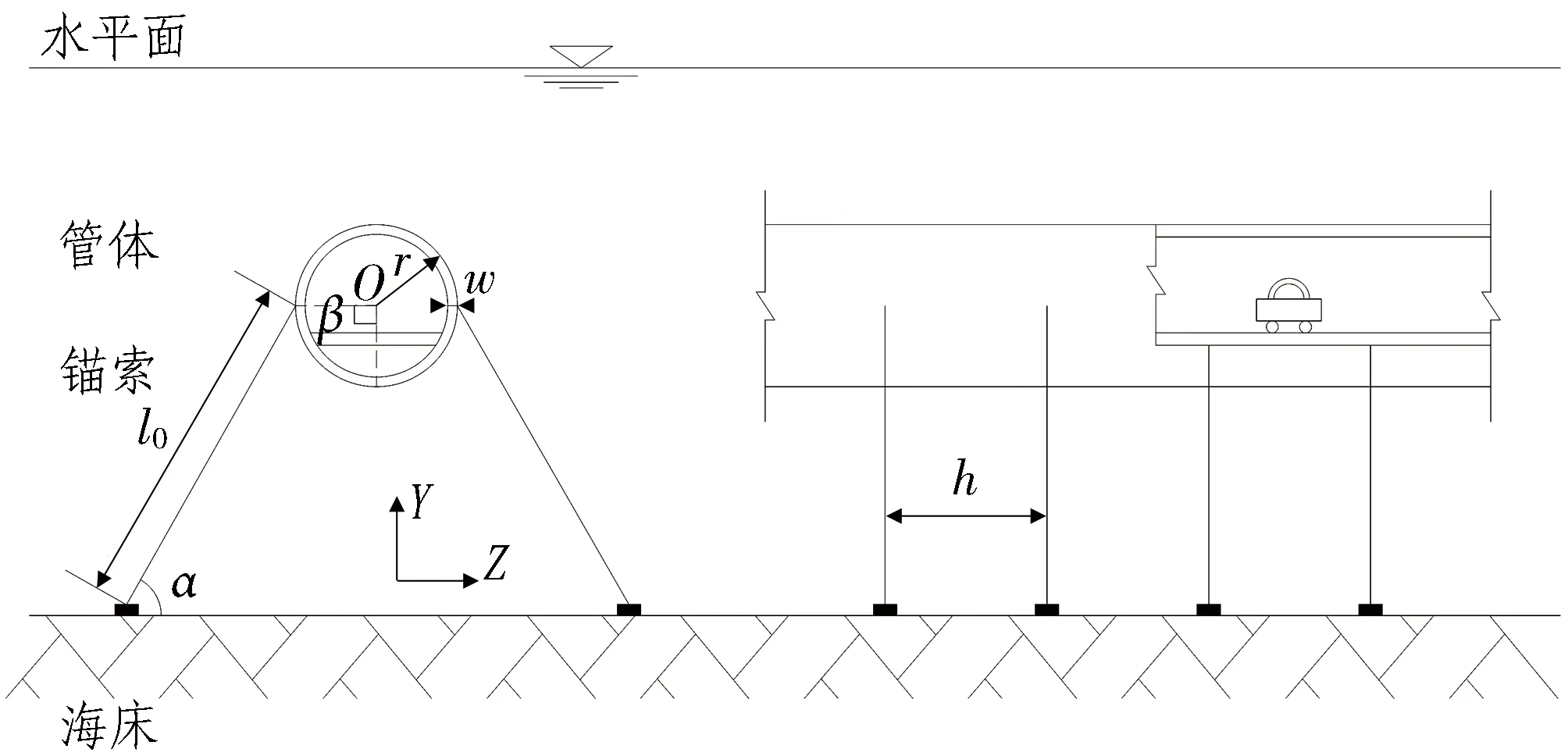
l0为锚索长度; α为锚索倾角; β为锚索安装角; r为管体半径; w为管体壁厚; h为锚索间距。

1.2 有限元模型和松弛判据

采用ABAQUS软件建立有限元模型,其中,管体采用梁单元B31模拟,锚索采用桁架单元T3D2模拟。整体模型共划分为2 038个单元,总节点数为6 077个。管体两端为简支边界,锚索与管体之间通过MPC约束实现铰接,锚索与基础铰接。悬浮隧道有限元模型如图2所示。

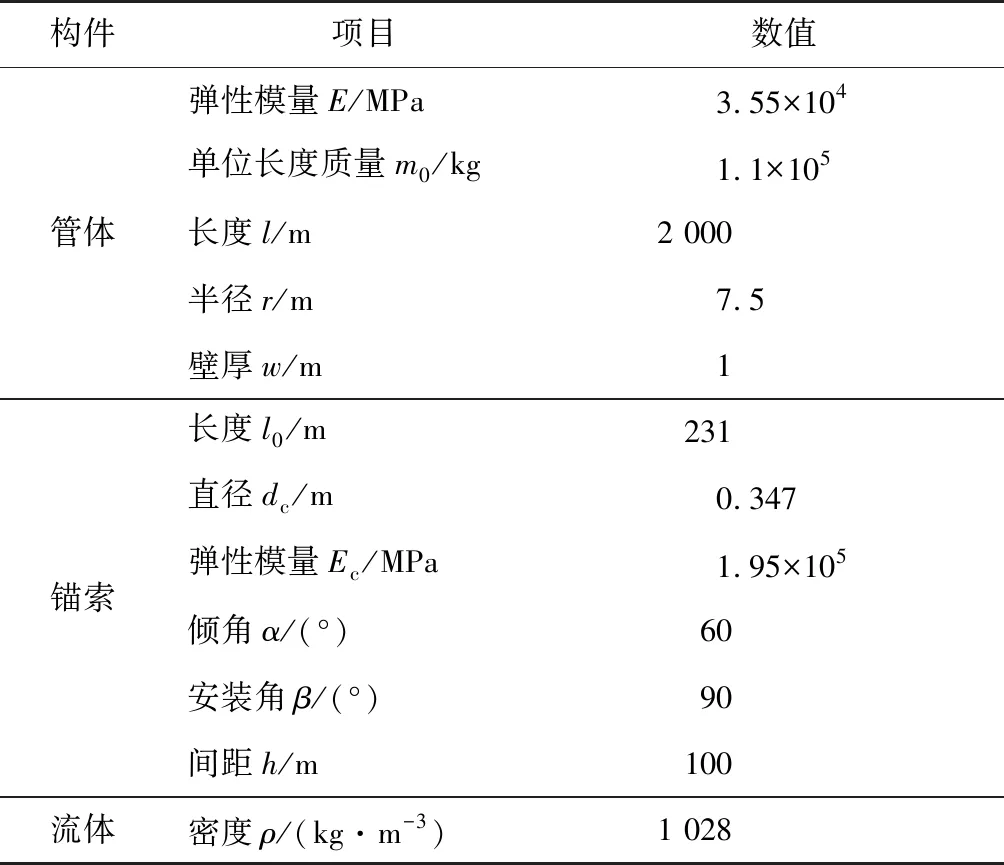
表1 悬浮隧道基本参数

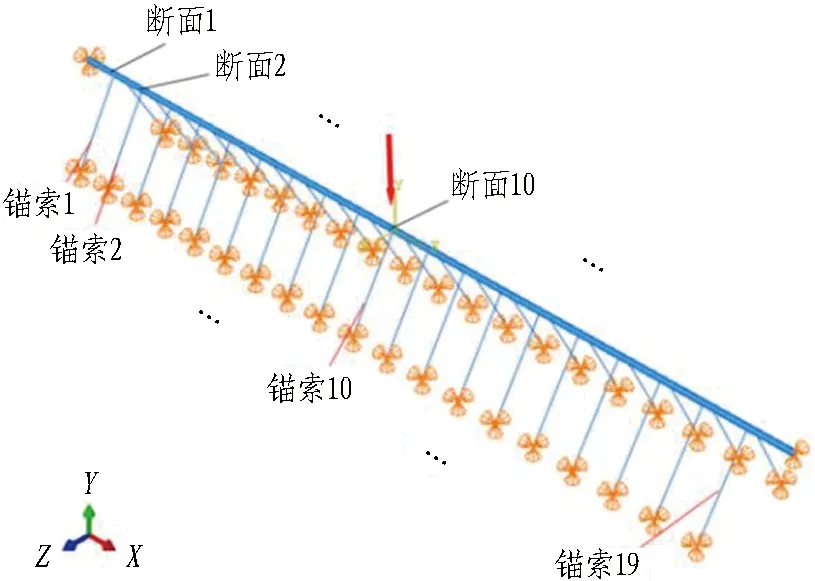
图2 悬浮隧道有限元模型

为分析对比锚索松弛效应对悬浮隧道冲击动力响应的影响,设置2种锚索刚度变化情况。

1)不考虑松弛。忽略索力变化对轴向刚度的影响,假定锚索刚度不变,且可以承受轴向压力。

2)考虑松弛。锚索和管体位移关系如图3所示。在竖向冲击荷载作用下,管体产生向下位移u,当锚索的伸长量Δli≤0时,其索力为0,即产生松弛现象。第i根锚索的刚度表达式[11]为:

(1)

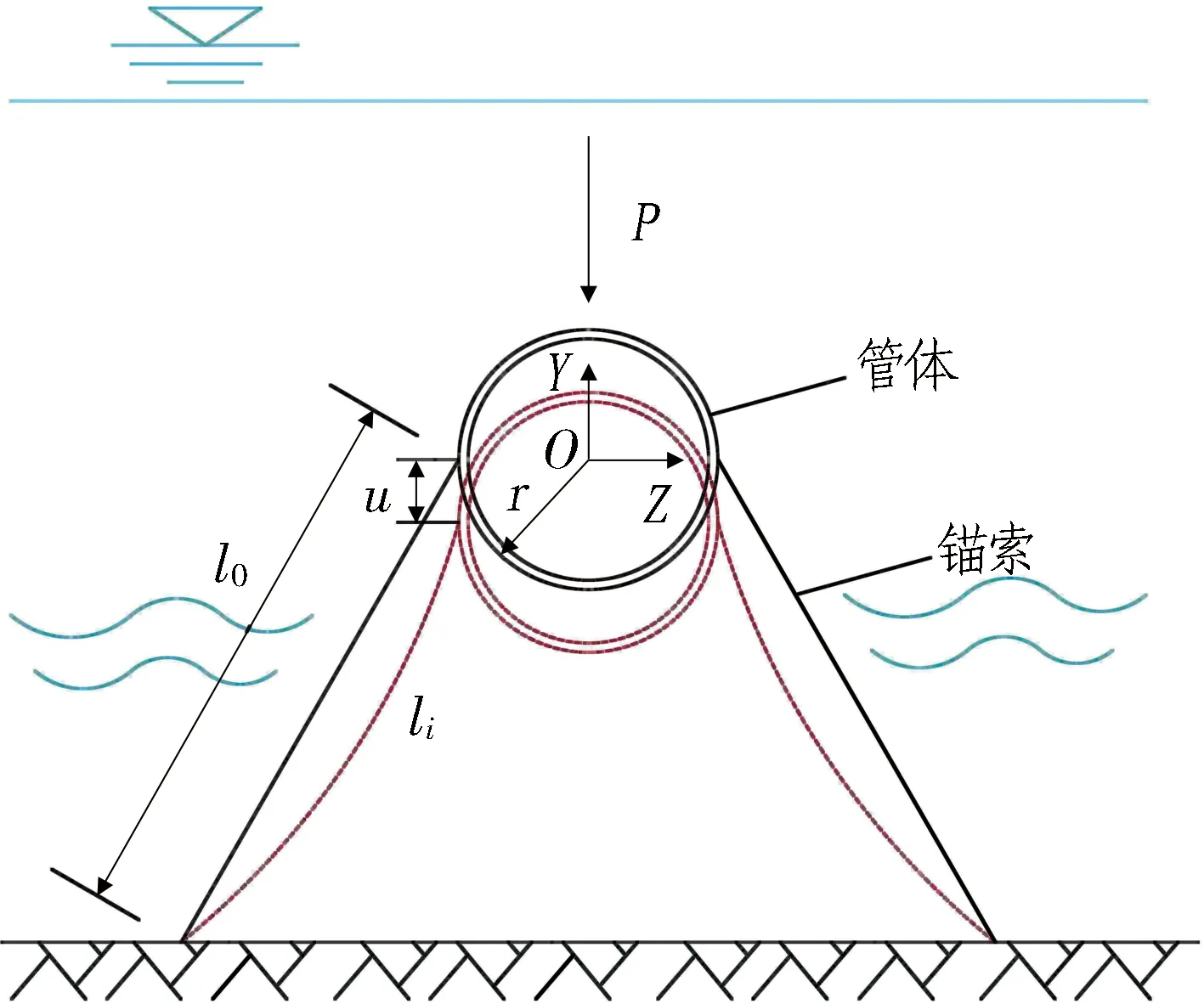
u为管体竖向位移; P为冲击荷载。

其中,

(2)

式(1)—(2)中:k为锚索的抗拉刚度;li为第i根锚索的瞬时长度;ln为无应力长度;E为锚索弹性模量;A为锚索横截面积。

1.3 荷载施加

1)静力荷载。在ABAQUS中荷载模块为悬浮隧道施加静力,包括浮力及重力,模拟悬浮隧道结构在静水中的受力状态。

2)流体惯性力。流体惯性力通过在ABAQUS截面属性模块中设置浸没截面来实现。

3)流体阻力。流体阻力采用UAMP子程序进行计算,每一步增量中利用ABAQUS中的Sensor功能记录当前时刻管体不同位置的竖向运动速度值,传递给UAMP子程序;在子程序中基于Morison方程计算该时刻相应的流体阻力幅值并反馈给ABAQUS主程序作下一步结构分析,达到模拟流体和结构相互作用的效果[5]。与传统CFD方法相比,本方法省略了耗时较多的流场分析,计算量和计算效率能得到显著优化。

4)冲击荷载。以幅值的方式加载矩形冲击荷载,作用位置为管体跨中处。冲击荷载作用时程图如图4所示。

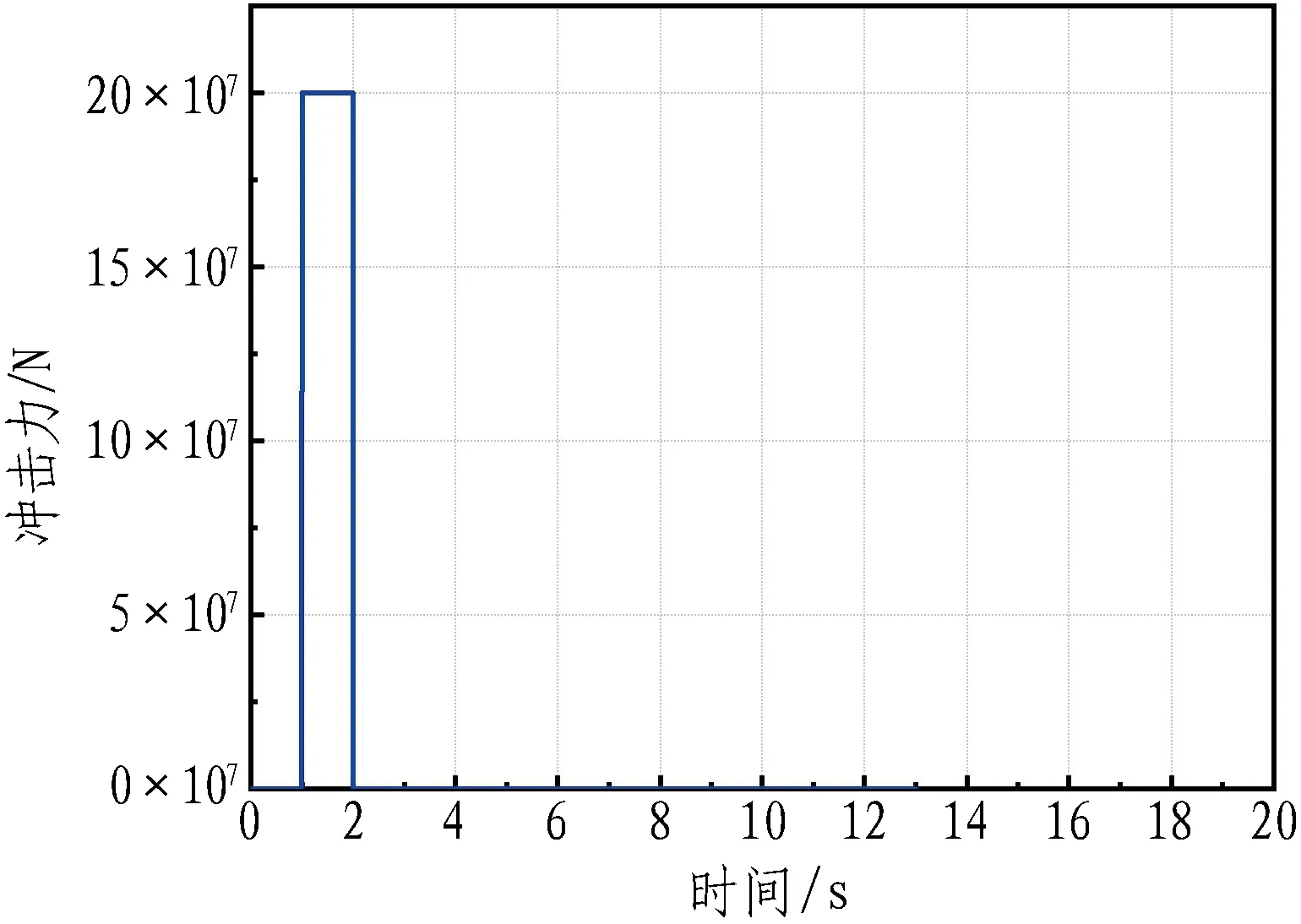
图4 冲击荷载作用时程图

悬浮隧道在冲击荷载作用下考虑锚索松弛效应的动力响应数值模拟分析流程图如图5所示。

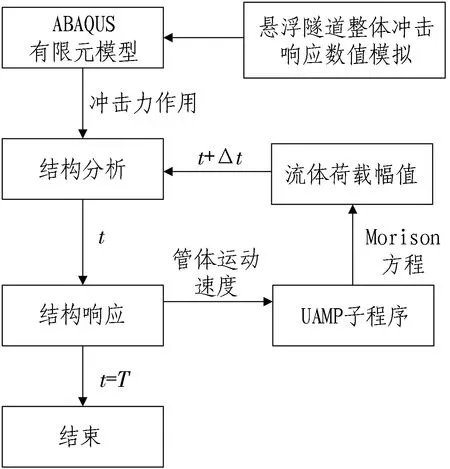
t为时间; T为计算总时间; Δt为时间增量。

2 计算结果与分析

2.1 锚索索力

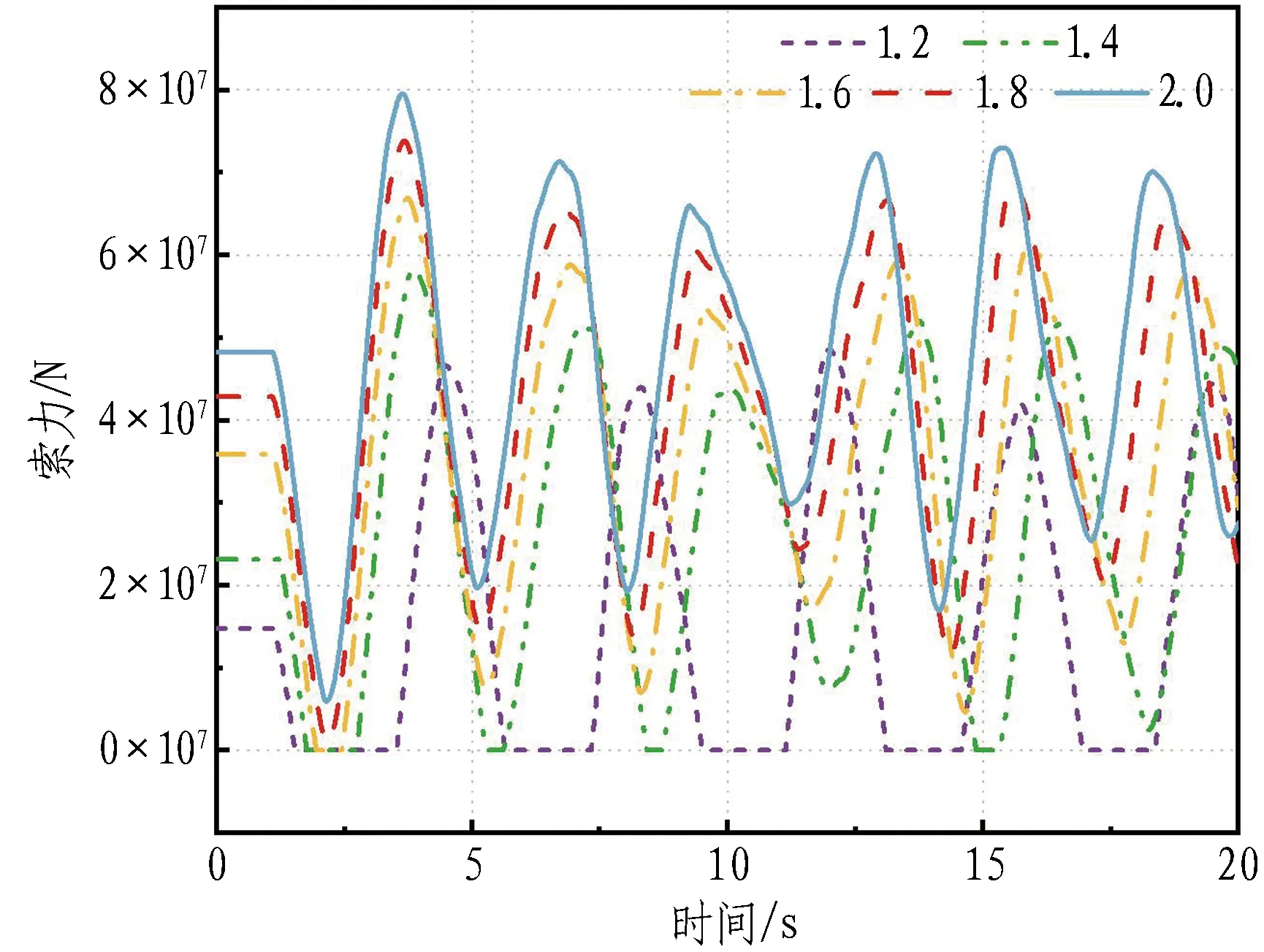
冲击荷载作用点处锚索索力时程曲线及各锚索最小索力分布如图6和图7所示。

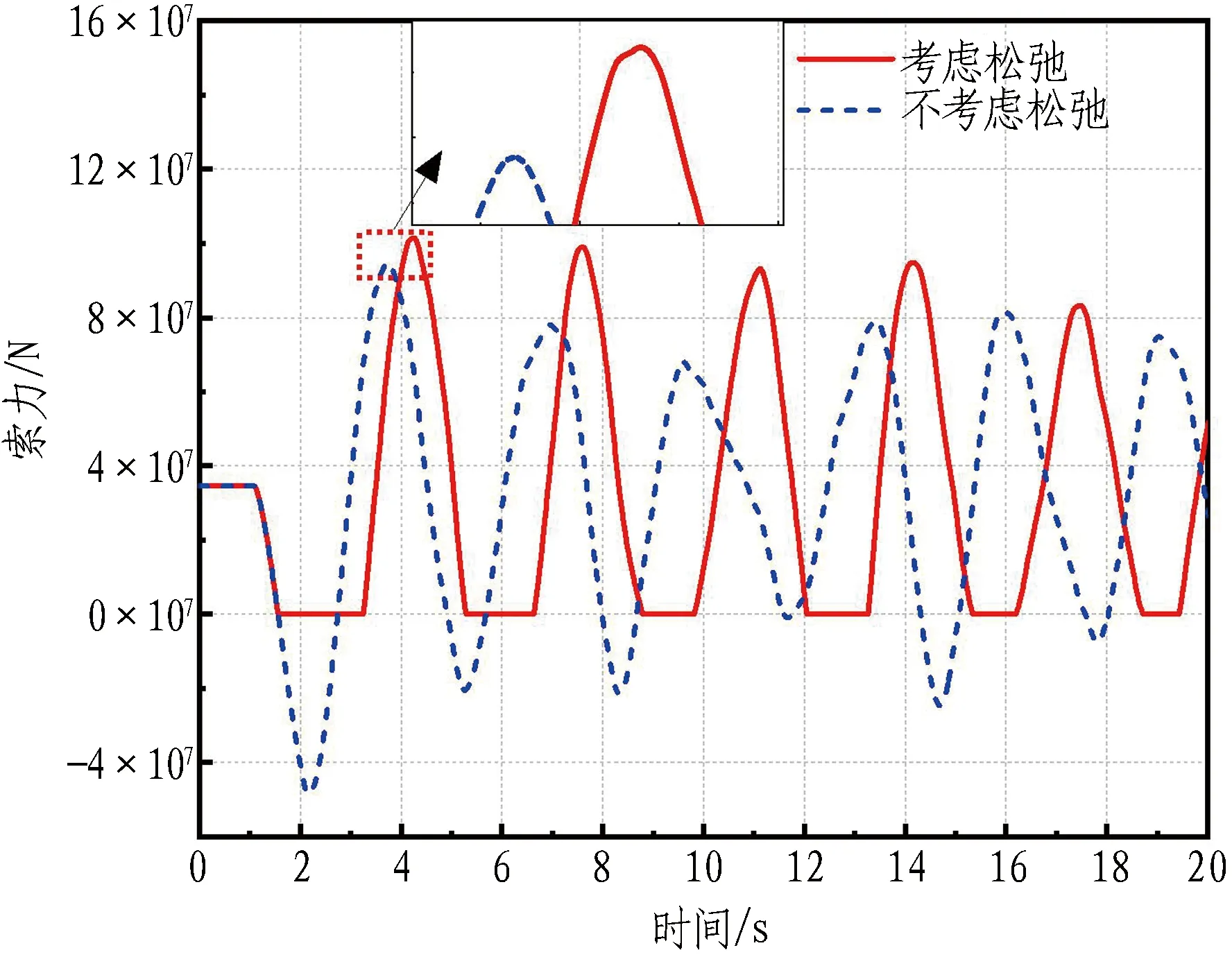
图6 冲击点锚索索力时程曲线

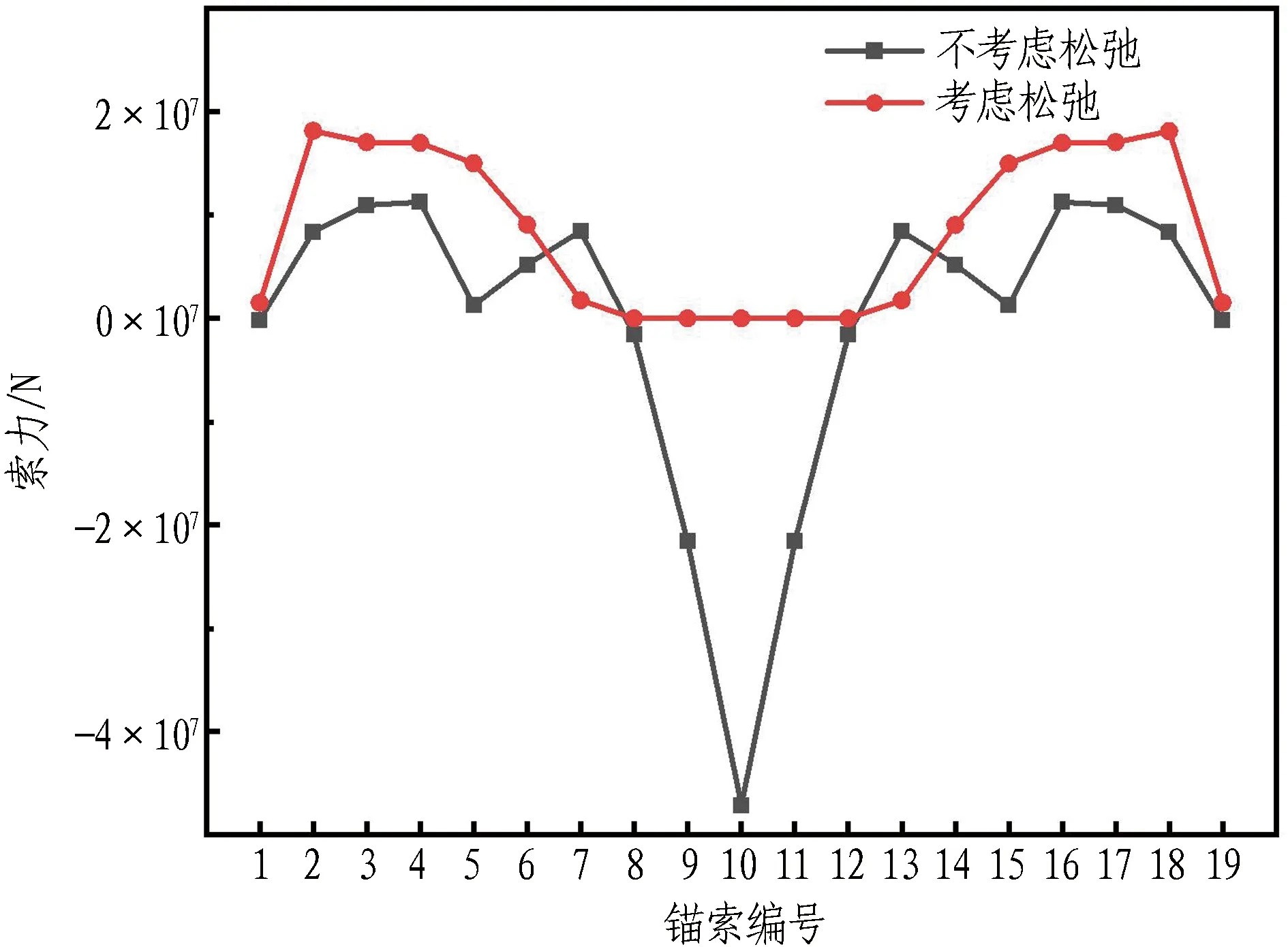
图7 冲击荷载作用下各锚索最小索力分布

由图6可知: 在冲击荷载作用下,考虑松弛的悬浮隧道锚索多次出现索力为0的情况,表明锚索会呈现交替的松弛与张紧状态;锚索最大索力通常出现在冲击荷载作用后的第1个振动周期内,考虑松弛和不考虑松弛时的锚索最大索力分别为1.02×108N和0.95×108N,增幅为7.09%。根据计算,最大应力分别为1.004×103MPa和1.078×103MPa,尽管尚未达到锚索极限抗拉强度,但松弛现象会导致锚索冲击张力增大,对结构安全不利。

由图7可知,冲击荷载使得作用点附近5对锚索产生松弛现象,而远离冲击荷载作用点处锚索虽未松弛,但索力仍存在一定幅度的变化,表明冲击荷载对悬浮隧道的影响范围较大。

2.2 管体位移

锚索松弛会导致其对管体的支撑作用消失。冲击荷载作用点处的管体位移时程曲线及位移最大时刻管体变形曲线如图8和图9所示。

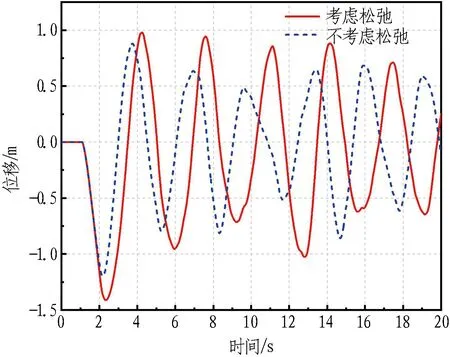
图8 冲击点管体位移时程曲线

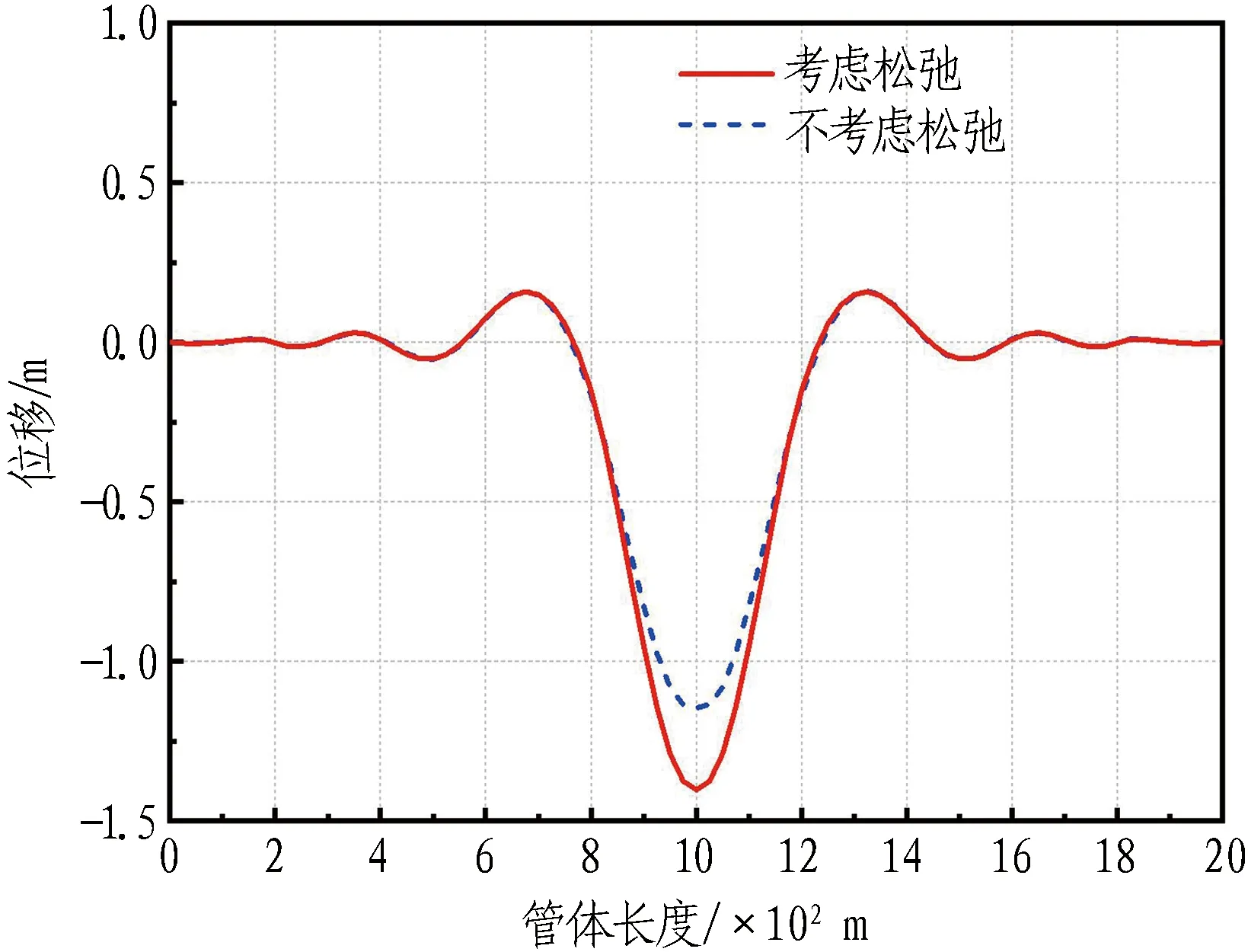
图9 冲击点位移最大时刻管体变形曲线图

由图8可知,管体位移与索力的响应变化特征相近。由于锚索松弛后对管体支撑刚度的减弱,结构振动周期增大,考虑松弛的模型位移响应略滞后于不考虑松弛的模型。在振动过程中,考虑松弛时管体的位移幅值均大于不考虑松弛时的情况。由图9可知: 在冲击荷载作用位置会产生最大管体竖向变形;不考虑松弛的管体位移为1.2 m,考虑松弛的管体位移达1.4 m,增幅达16.67%,管段两端位移曲线基本吻合,受松弛影响不大。总体来说,锚索松弛的影响不可忽略,应引起设计的注意。

3 影响因素分析

3.1 冲击荷载对动力响应的影响分析

为讨论冲击荷载大小对考虑锚索松弛的悬浮隧道冲击动力响应的影响,采用5种不同大小的冲击荷载进行数值模拟,管体浮重比为1.6,锚索倾角为60°,结果如图10所示。

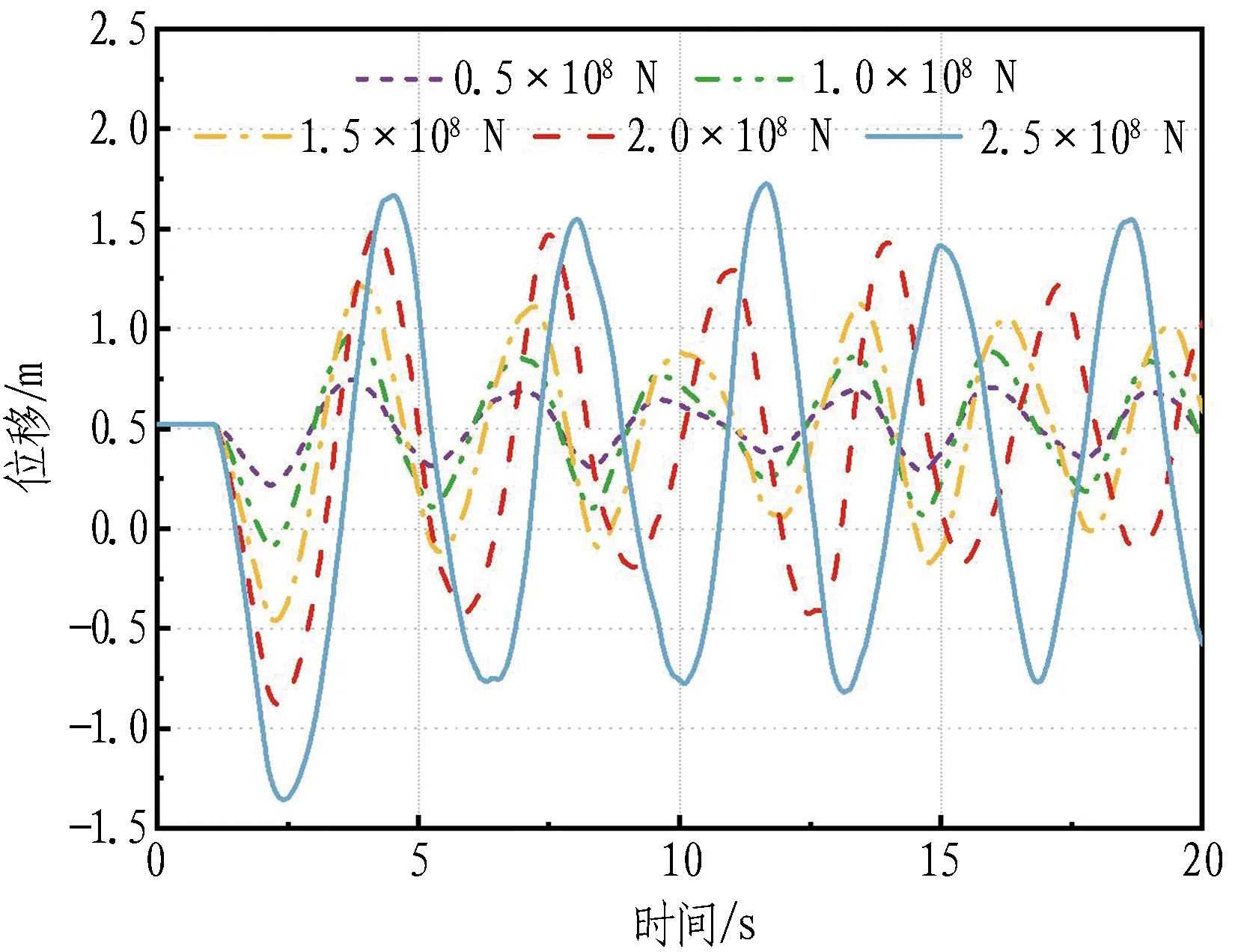
(a) 冲击点管体位移时程曲线

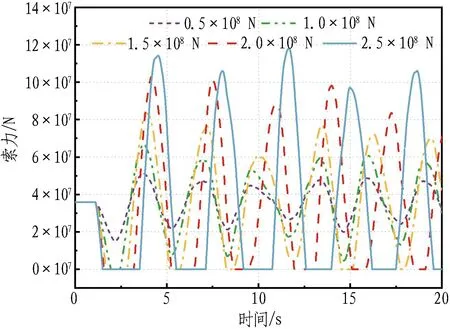
(b) 冲击点锚索索力时程曲线

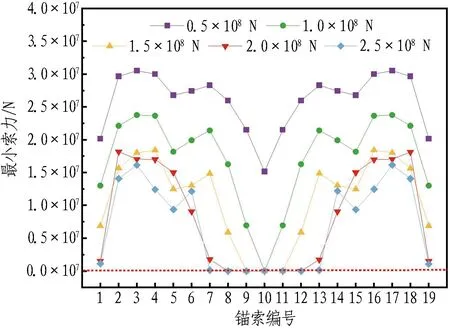
(c) 锚索最小索力

由图10(a)可知,增大冲击荷载会直接导致管体位移增大,进而对锚索索力产生影响。由图10(b)和图10(c)可知: 仅在冲击荷载为0.5×108N时,锚索索力始终大于0;随着冲击荷载的增大,冲击点处的锚索率先出现松弛,且松弛锚索数量逐渐增多;当冲击荷载达到2.5×108N时,共有7对锚索出现松弛,最大索力较初始索力增大217.59%。同时,索力的恢复时间增长,且在更多振动周期中出现锚索松弛-张紧状态的转换,对悬浮隧道结构安全产生不利影响。

冲击荷载为2×108N时,不同作用时长下对动力响应的影响如图11所示。

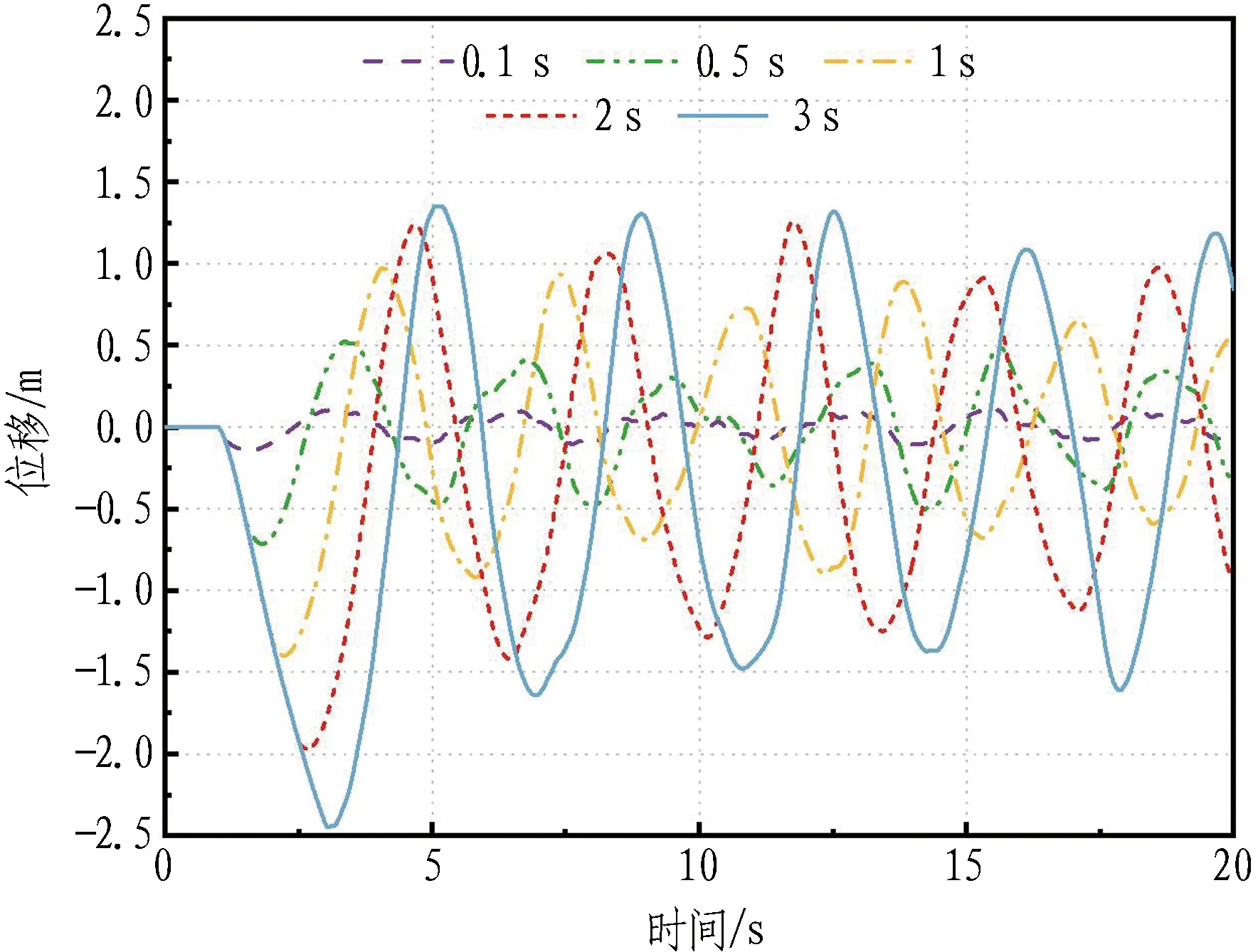
(a) 冲击点管体位移时程曲线

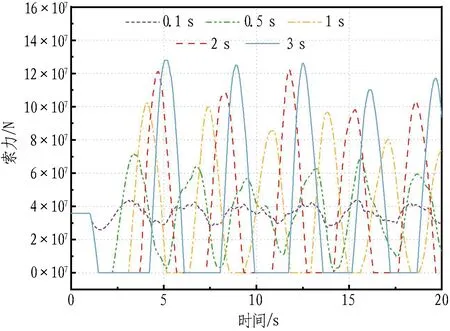
(b) 冲击点锚索索力时程曲线

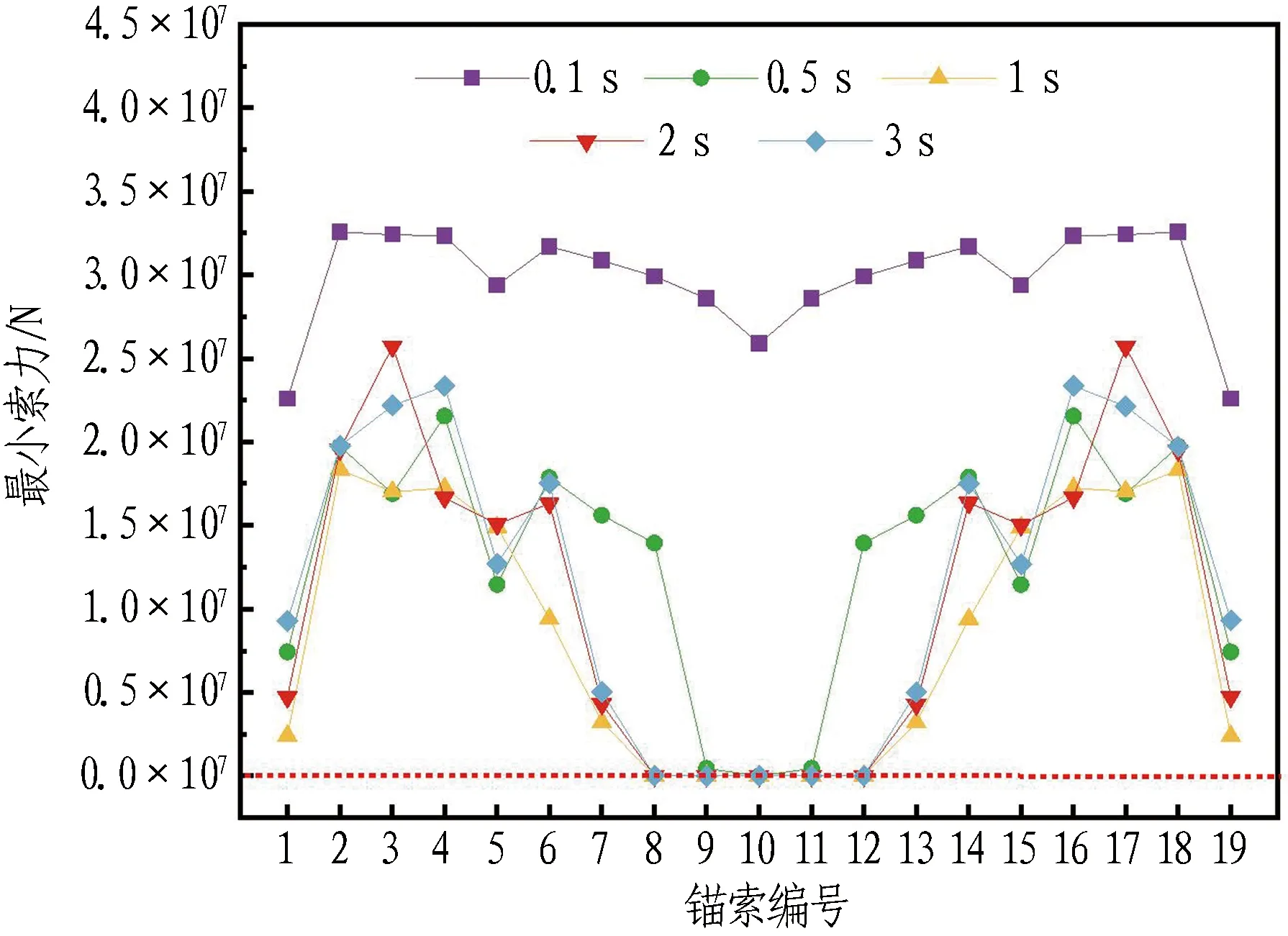
(c) 锚索最小索力

由图11可知: 冲击点管体最大位移会随荷载作用时间的增长而增大;当冲击时间很短时,由于管体变形量很小,锚索不会出现松弛,锚索松弛时间和冲击张力相应增大,但增幅逐渐减慢;当冲击时间大于1 s时,锚索松弛范围不再增大,这是由于随着作用时间的增长,冲击荷载逐渐表现出静力荷载的特性,管体变形和锚索松弛范围趋于稳定。

3.2 浮重比对动力响应的影响分析

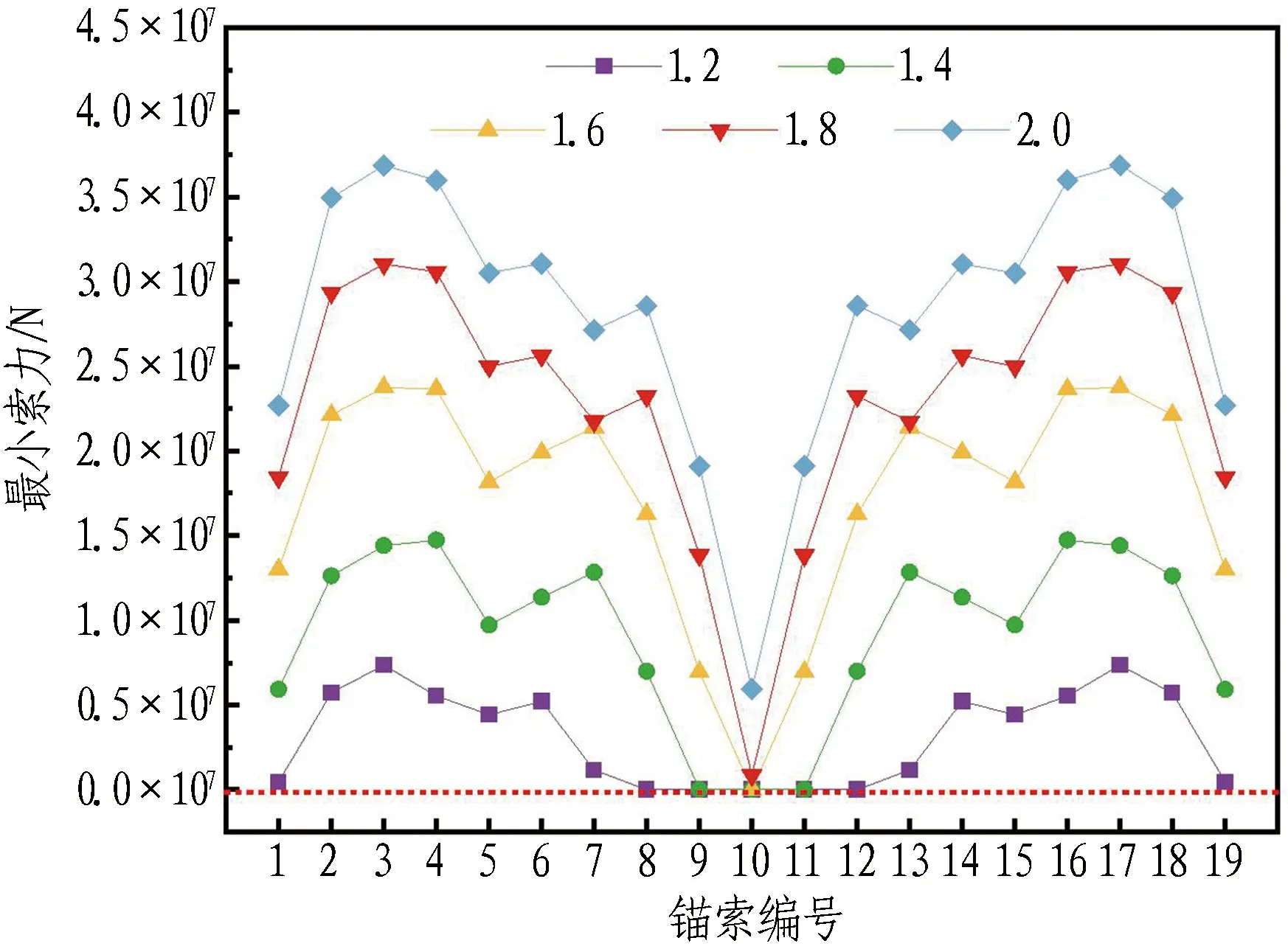
浮重比是悬浮隧道结构设计的重要参数,合适的浮重比可以提供足够的多余浮力,从而保证结构的稳定性。冲击荷载为1×108N、锚索倾角为60°、浮重比在1.2～2.0[16]变化时悬浮隧道的冲击动力响应如图12所示。

(a) 锚索最小索力

(b) 冲击点索力时程曲线

由图12(a)可知: 较大的浮重比会增加锚索初始索力,有利于锚索保持张紧的状态;当浮重比为1.2时,8—11号锚索最小索力降至0,发生松弛;随着浮重比的增加,松弛的锚索数量减少;当浮重比大于1.8时,锚索在冲击荷载作用过程中一直保持张紧状态。由图12(b)可知: 增大浮重比可缩短每一次锚索松弛的持续时间;锚索索力变化幅值随浮重比的增大而降低;当浮重比为1.2时,锚索的最大索力增幅为初始索力的214.19%;当浮重比为2.0时,锚索索力的变化幅值约为初始索力的64.94%。因此,增大浮重比对减小锚索松弛范围有利,会增大初始索力。综合考虑安全性和经济性,建议浮重比的取值为1.4左右。

3.3 锚索倾角对动力响应的影响分析

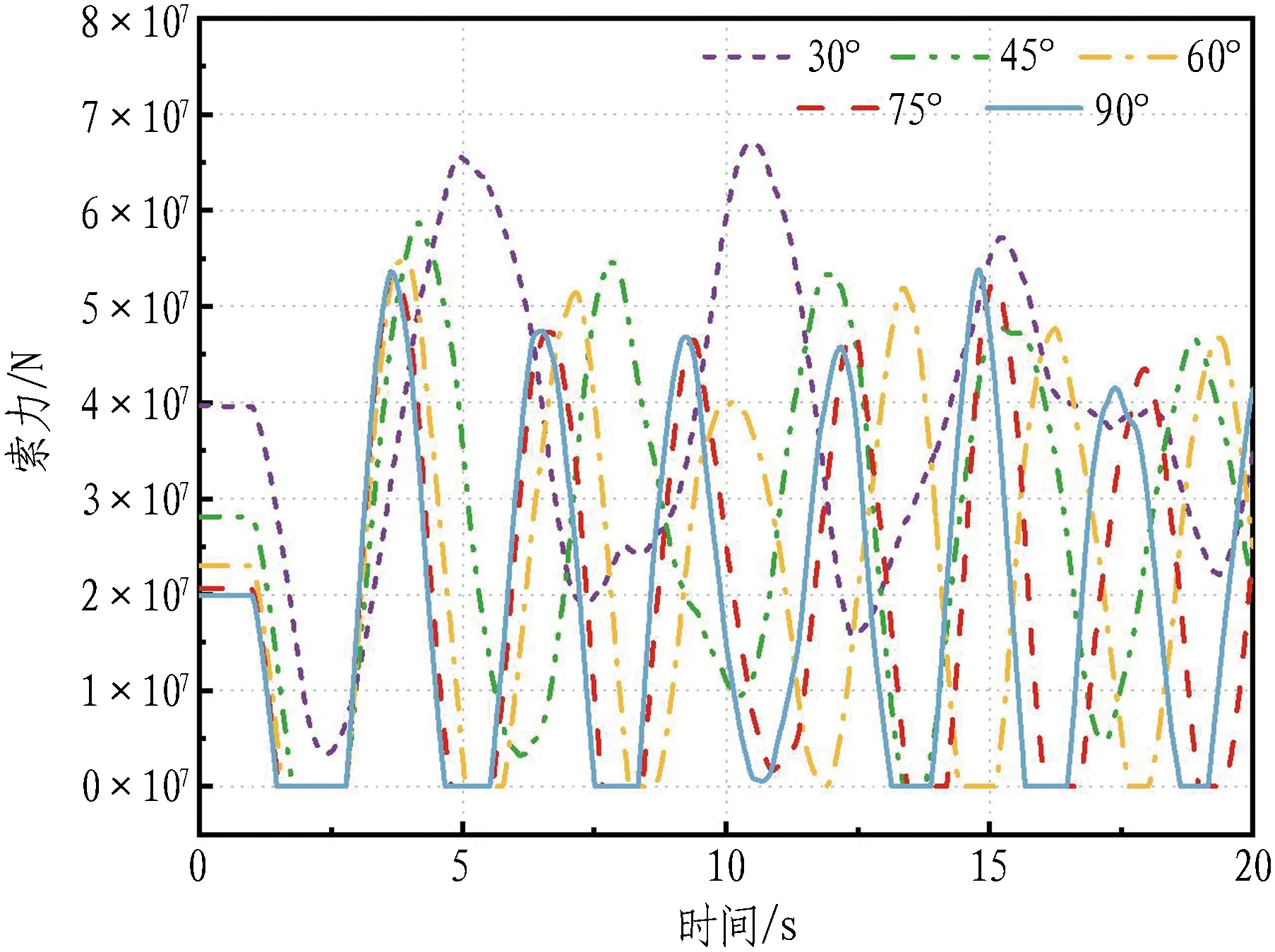
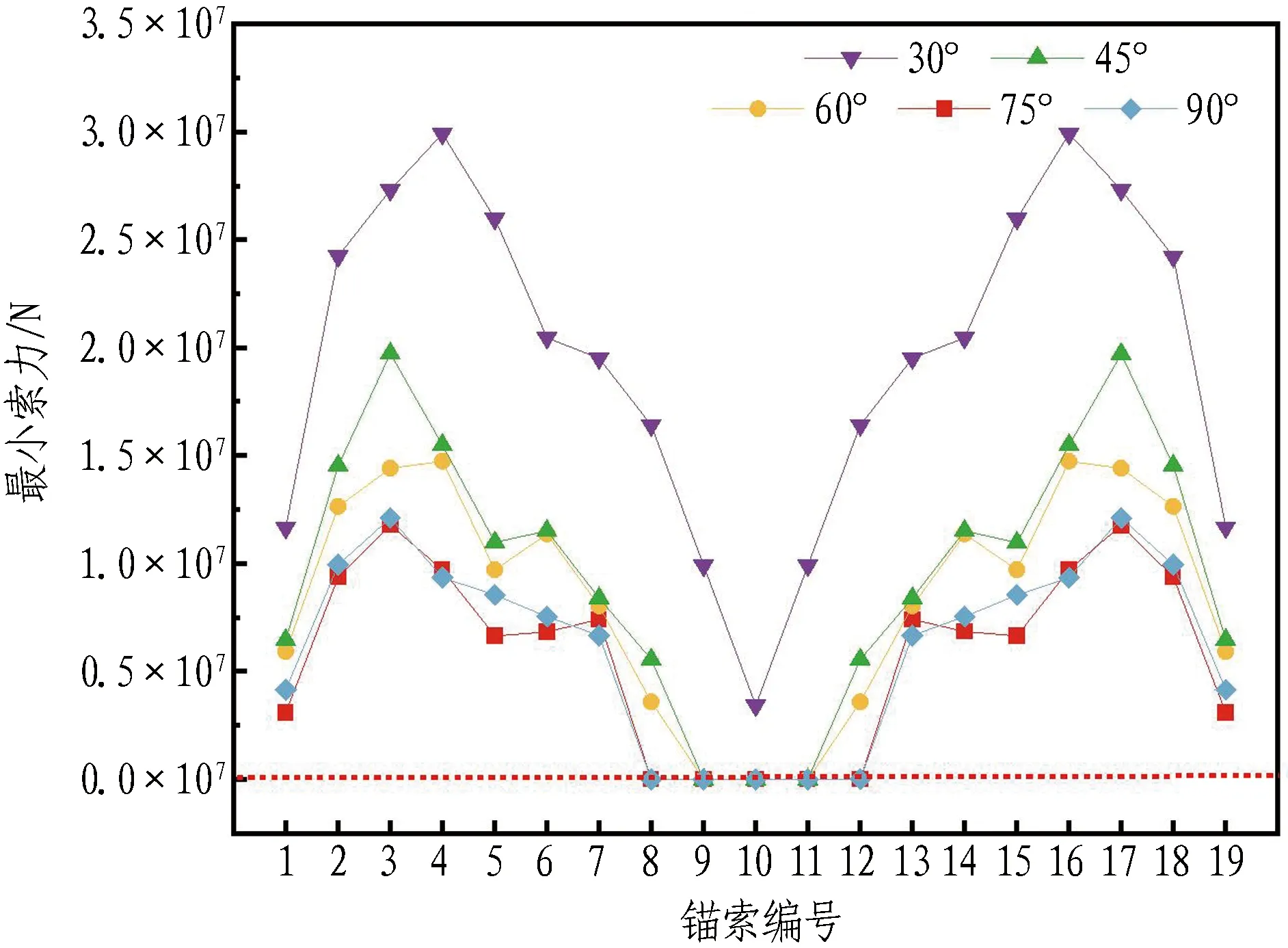
冲击荷载为1×108N、浮重比为1.4时,不同锚索倾角对考虑锚索松弛的悬浮隧道冲击动力响应影响情况如图13所示。

(a) 冲击点索力时程曲线

(b) 锚索最小索力

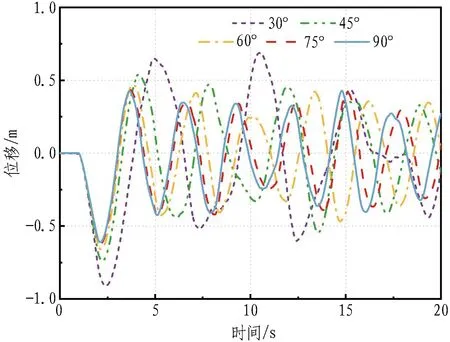
(c) 冲击点位移时程曲线

由图13(a)和图13(b)可知,在竖向冲击荷载作用下,只有锚索倾角为30°时其索力始终大于0,且随着倾角的增大,松弛的锚索数量逐渐增多。这是由于当锚索倾角较大时,管体竖向位移对其轴向变形的影响更为显著,使其更易松弛。但从管体位移来看,较大的锚索倾角能提供足够的竖向支撑刚度,有利于减小管体竖向位移,如图13(c)所示。不同倾角对应的锚索初始参数如表2所示。当锚索倾角小于45°时,在相同管体浮重比和深度下,初始索力和锚索长度会迅速增大,不利于锚索布置。因此,综合考虑结构受力和布置,并尽量减小锚索松弛的影响,建议锚索倾角的取值为45°～60°。

表2 不同锚索倾角情况下索力和长度取值

Table 2 Cable force and length values of anchor cable with different inclined angles

锚索倾角/(°)初始索力/N锚索长度/m303.97×107400.00452.81×107282.84602.30×107231.00752.06×107207.06901.99×107200.00

4 结论与讨论

本文采用ABAQUS数值模拟方法对考虑锚索松弛的悬浮隧道冲击动力响应进行研究,分析冲击荷载、浮重比、锚索倾角等因素对动力响应的影响,得到以下结论。

1)在冲击荷载作用下,悬浮隧道锚索会发生松弛现象。锚索松弛会增大结构整体动力响应,最大位移增幅达10%以上。在锚索松弛-张紧过程中,最大索力也会因考虑松弛而增大。

2)增大冲击荷载及冲击时长均会使管体位移、锚索松弛时间和范围增大,对结构不利,但冲击时间对结构的影响会随着时间的增长而逐渐稳定。

3)尽管较大的管体浮重比会增大锚索初始索力,但有利于提高索力储备,减少锚索松弛现象和振动过程中最大索力的增幅。综合考虑安全性和经济性,设计时建议浮重比取值为1.4左右。

4)在竖向冲击荷载作用下,锚索倾角越大,越容易发生松弛,而较小的锚索倾角会导致初始索力、锚索长度和管体竖向位移增大,且不利于锚索布置。因此,建议锚索倾角的取值为45°～60°。

在严重的碰撞事故中,除了会发生锚索松弛外,悬浮隧道管体因材料损伤引起的结构刚度变化通常也不可忽略,如何模拟局部损伤对管体抗弯刚度的影响,需在悬浮隧道整体冲击响应分析中进一步深入研究。