某变速抽蓄机组水泵水轮机发电工况压力脉动试验研究

李 瑶，马智杰，2，3，孙博志

(1.中国水利水电科学研究院，北京 100038；2.天津大学电气自动化与信息工程学院，天津 300072；3.华北电力设计院有限公司，北京 100120)

0 引 言

大力开发可再生能源是我国能源发展的重要战略举措。未来能源架构将以风光可再生能源为主，要维持电网稳定，大规模的灵活调节电源必不可少。抽水蓄能电站运行可靠、应用规模大，是到现在为止公认的最成熟、最经济、容量最大的储能方式，为维护电网稳定做出了巨大贡献，在调峰填谷以及提供和吸收新的储能方面发挥了综合作用[1-2]。截至2022年底我国可再生能源的发展情况如图1所示，可见风电加光伏能源的总装机容量占比已增至63%，发电占比增至44%，其发展势头较为迅猛，为加快我国抽水蓄能电站建设奠定了一定的工程背景。

图1 截至2022年底我国可再生能源发展情况

电站中的水力发电机组根据其运行特点可分为常规定速机组和变速机组。变速机组又分为变级调速和连续调速。与定速机组的外部特性相比，变速机组可以更充分地利用其输出能力，改变机组转速，改善转轮内部流态，以提高偏心工况下的运行效率。在调节特性方面，变速机组可以实现快速的功率跟踪，并突出响应灵活性。为了提高水电机组的调控能力，发达国家大力推动变速恒频抽水蓄能技术的发展[3]。日本为变速水电机组建设与发展大国，截至2020年，投产运行变速机组容量已接近2 200 MV·A[4]。欧洲中德国瑞士法国等对变速水电技术开展的研究也较为成熟，近年投运进程较快[5]。我国的变速恒频抽水蓄能技术起步较晚，与国外还有一定差距。我国的丰宁抽水蓄能电站位于河北省丰宁满族自治县境内，是世界上装机容量最大的抽水蓄能电站，其两台变速机组为中国首次建设的大型交流励磁变速抽水蓄能机组。国际上采用全功率变频变速可逆式抽水蓄能机组的电站仅有1个改造项目，为瑞士的Grimsel 2号电站，它将原有的1台90 MW定速机组改装为100 MW 的全功率变频变速抽水蓄能机组，在水泵功率连续变化方面取得了良好的效果[6]。

变速机组转速可调的特性使其在维持偏工况运行稳定性以及机组效率等方面都有很大作用。例如，周喜军等[7]发现事故甩负荷时，当初始转速在一定范围内增加，变速机组的最高转速不会显著上升。Valavi等[8]认为，变速操作对维持水轮机效率有很大帮助，即使水头和输出发生变化，水轮机运行在其他偏工况下，水轮机的效率仍然可以保持在较高水平。随着可变可再生能源在电网中的日益普及，这些研究成果为水电机组的变速运行提供了参考。

压力脉动是由转轮、叶片以及其他部件之间的静态和动态干扰引起的一种压力波动现象，该现象会引起机组的振动和疲劳失效，甚至引起厂房的振动，极大地影响电站的安全稳定运行[9]。Trivedi等[10-11]研究了混流式水轮机转速变化过程中不同区域的压力随时间的变化规律，得出过渡过程中动静干涉的幅值很小，但在过渡周期结束时，幅值会迅速增大的结论；此外，在无叶区和转轮中，压力脉动幅值随转轮转速的增大而增大。王彤彤等[12]研究发现，变速运行模式可以减弱(甚至消除)尾水管涡带；在最佳转速下，效率得到提升，机组运行的稳定性也得到提高。此外，变速运行模式还可以提高水轮机的效率，降低能耗，提高机组的经济性。因此，采用变速运行模式是优化水轮机设计和提高机组运行效率的有效途径之一。

目前水泵水轮机压力脉动的研究方法主要有传统的理论分析方法、试验研究方法与数值模拟方法。试验研究方法多为物理模型试验[13-14]，数值模拟研究[15-16]水泵水轮机内部流动特性的主要工具是ANSYS软件。

本文对水泵水轮机真机在发电工况寻优变转速运行之后的各部位压力脉动进行分析。现场机组试验从1～5 MW，转速从814.8 r/min提高至926.5 r/min，导叶开度从18.9%到58.7%，当功率达到1、2、3、4 MW及5 MW时，机组在此工况下稳定运行一段时间，取该段时间的蜗壳进口、无叶区及尾水管出口的压力数据进行不同部位压力脉动的比较分析。通过分析全功率变速抽水蓄能机组水泵水轮机发电工况变速运行模式的压力脉动，探究在发电工况变速运行过程中水泵水轮机的压力脉动对机组安全稳定运行的影响。

1 试验方法介绍

1.1 现场情况

春厂坝原为常规水电站，图2为其厂房内部及水泵水轮机照片，该电站安装3台18 MW的常规水轮机组，新装1台5 MW变速可逆式抽蓄机组。抽蓄机组抽水最大功率6.7 MW，发电额定功率5 MW。其运行特点为：以水轮机发电为主，水泵抽水为辅。

图2 春厂坝水电站

春厂坝变速机组充分利用全功率变频变速的优势，采用变转速-变导叶开度双寻优为手段的全路径寻优，使水轮机实际运行工况均处于水轮机特性的最佳运行区域，避开全特性曲线上可能存在的S形特性区域，避开压力脉动幅值大的区域。全功率变频变速抽水蓄能机组水轮机工况全路径优化主要包括变转速寻优线以及最低单位转速启动运行线。

变转速寻优线基于以兼顾水轮机工况运行的高效稳定性和操控实用便捷的可操作性为原则，以变转速-变导叶开度双寻优为手段，实现了水轮机运行范围内不同水头和不同出力时对应的最佳转速的设置，使水轮机实际运行区域接近为水轮机特性的最优区域。该路径使水轮机稳态运行时始终处于相应出力(相应导叶开度)下的最优效率区域。最低单位转速启动运行线为水轮机模型综合特性曲线上的一条同时满足水轮机快速平稳并网和小开度部分负荷高效稳定运行的等单位转速线。

1.2 试验介绍

春厂坝水泵水轮机主要参数：叶片数7个，转轮进口直径D1为1.08 m，转轮出口直径D2为0.708 48 m，额定转速n为1 000 r/min，固定导叶和活动导叶数均为20个，额定流量为4.75 m3/s，额定水头为130 m，水轮机工况额定比转速为166 m·kW，水泵工况最低扬程工况比转速为43.6 m·kW。

本次机组稳定性试验为变功率试验，试验工况点为有功功率阶梯式升至最高负荷。在机组有功功率分别稳定在1、2、3、4 MW及5 MW时，抽取传感器数据，记录水头、转速等数据见表1，传感器采样频率为1 000 Hz。

表1 不同工况外部数据

由表1可以看出，在有功功率为1、2 MW和3 MW时转速没有太大变化，这是因为考虑到机组的水力稳定性，变转速寻优设置了最低单位转速启动运行线。水轮机出力、单位转速、单位流量以及单位转速及单位流量的关系见式(1)～(4)，根据上述公式，水轮机启动工况及低负荷运行工况均可根据水头计算出对应的转速运行在该最低等单位转速线上，有功功率为1、2、3 MW时即为低负荷运行工况，运行时都处于同一单位转速线上，由于有功功率为1、2、3 MW时水头相同，其转速也基本相同。

水轮机出力

P=γ·Qi·Hi·η

(1)

单位转速

(2)

单位流量

(3)

Q11～n11关系

(4)

式中，γ为ρg，常取9.81；Q为流量，m3/s；H为水头，m；η为水轮机的效率；n为机组转速，r/min；D1为转轮进口直径，m。

试验共设置压力脉动监测点3个，分别位于蜗壳进口处、导叶后转轮前无叶区处以及尾水出口处，图3为水泵水轮机传感器位置示意图。

图3 传感器位置

1.3 分析方法

压力脉动的分析方法主要有时域法和频域法，时域法即相应物理量随时间变化的过程，以时间为横坐标，绘制曲线，频域法即使用FFT快速傅里叶变换将压力脉动的时域信号转换为频域信号，从而得到以频率为横轴，相对应幅值为纵轴的频域图[64]。

在数据分析时，采用无量纲数压力系数Cp作为量化水泵水轮机压力脉动强度的参考值，该系数表达式为

(5)

2 相同工况下水泵水轮机不同部位压力脉动分析

选取相同工况下水泵水轮机不同部位的压力值进行压力脉动分析。即在同样的P=1～5 MW的工况下，将水泵水轮机蜗壳进口、无叶区及尾水管出口处的压力脉动进行对比分析。表2为不同工况下各部位的压力均值。

表2 不同工况各部位压力均值

2.1 时域分析

图4为P=1 MW和P=4 MW时在1 s内的各部位压力脉动时域图，为了更加直观地进行分析，从中截取转轮旋转一周时间内的时域图。图5分别为P=1、2、3、4 MW和5 MW时的蜗壳进口、无叶区、尾水出口压力脉动的时域图，横坐标约为转轮旋转一周所需的时间，纵坐标Cp为压力脉动系数。从图5可知，P=1 MW为低负荷运行工况，各部位的压力脉动相对比较杂乱，但仍可以看出，P=1 MW时的无叶区压力脉动与其他工况无叶区压力脉动一样，具有周期性，在转轮旋转的这一周里，其压力脉动系数峰值为3.654%和-2.668%，蜗壳进口处压力脉动系数峰值最大约在1%处；P=2 MW时无叶区压力脉动系数峰值为6.224%和-5.656%；P=3 MW时无叶区压力脉动系数峰值为6.849%和-7.917%；P=4 MW时无叶区压力脉动系数峰值为4.431%和-5.601%；P=5 MW时无叶区压力脉动系数峰值为4.459%和-5.790%。图5中无叶区压力脉动均具有明显周期性，且在转轮旋转一圈的时间内，其压力脉动均有7个波峰和7个波谷，即在转轮转一圈时间内，无叶区压力脉动经过了7个周期，可知其主频应为叶频。除最明显的无叶区外，从图4可以看出，尾水管处存在明显的低频压力脉动，时域图中蜗壳处压力脉动没有明显规律，且蜗壳与尾水管处压力脉动系数较无叶区来讲小了很多，可见离转轮越远，受到动静干涉的影响越小，压力脉动越不明显。

图4 1 s内各部位压力脉动时域

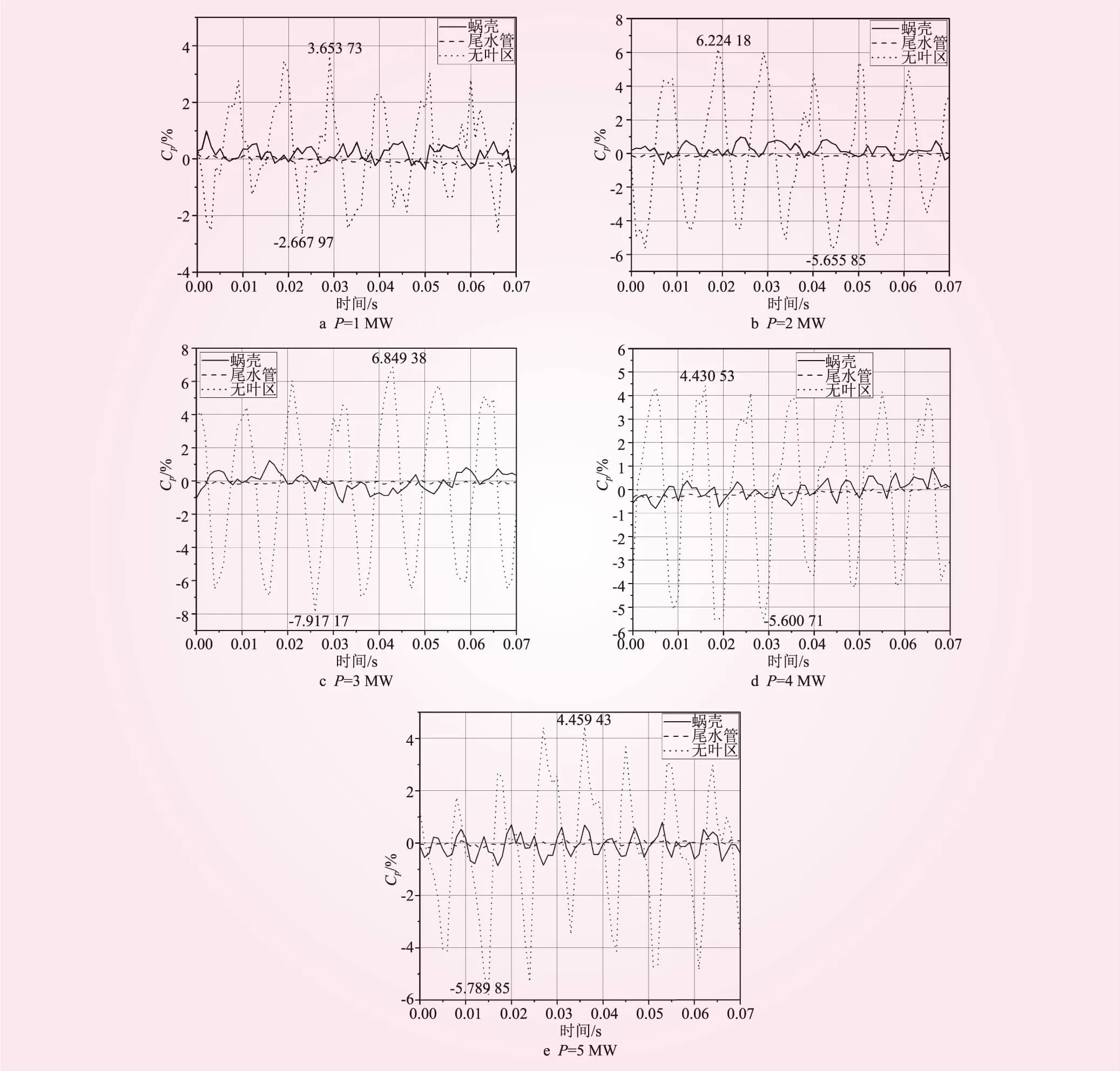
图5 转轮旋转一周各部位压力脉动时域

2.2 频域分析

为进一步了解各部位压力脉动的特性，将第2.1节得到的时域数据进行FFT快速傅里叶变换，得到各监测点压力脉动的频域图。图6分别为P=1、2、3、4 MW和5 MW时的蜗壳进口、无叶区、尾水出口压力脉动的频域图，横坐标为转频fn的倍数，纵坐标A为幅值。

图6 各部位压力脉动频域

从图6可知，P=1 MW时，无叶区压力脉动主频为7fn，次频为14fn，均为叶频倍数；蜗壳进口处主频为7fn；尾水管出口处主要为低频脉动，主频为0.4fn。P=2 MW时无叶区整数倍叶频压力脉动均较为明显，主频为7fn，次频为14fn，除此之外，21fn处压力脉动也非常明显；蜗壳进口处主频为7fn，次频为12fn；尾水管出口处主要为低频脉动，主频为0.3fn。P=3 MW时无叶区压力脉动主频为7fn，次频为14fn；蜗壳进口处主频为7fn，次频为12fn；尾水管出口处主频为0.3fn。P=4 MW时无叶区压力脉动主频为7fn，次频为14fn，28fn处压力脉动也比较明显；蜗壳进口处主频为0.3fn，次频为14fn；尾水管出口处主要仍为低频脉动，主频为0.3fn。P=5 MW时，图中无叶区压力脉动主频为7fn，次频为14fn，除此之外整数倍叶频压力脉动如21fn、28fn均非常显著；蜗壳进口处主频为12fn，次频为21fn；尾水管出口处主频为12fn，除此之外主要均为低频脉动，次频为0.3fn。

由图6可知，无叶区压力脉动主频均为7fn，蜗壳进口处压力脉动主频在转速与开度较小处为7fn。随着转速增大，导叶开度增大，其主频逐渐由7fn变为低频0.3fn或12倍频，相较于其他监测点，无叶区监测点受动静干涉影响明显，并且随着转速和导叶开度增大，无叶区14fn的压力脉动也随之越来越明显。尾水管出口处压力脉动幅值非常小，且主要为低频脉动，几乎不受动静干涉的影响。

2.3 整体分析

相同工况下，由上述时域频域图可以看出无叶区压力脉动是最严重的；除无叶区外，蜗壳也受到动静干涉的影响。无叶区位于转轮与活动导叶之间，受到的动静干涉影响最大，总的来说，离转轮区域越远，受到动静干涉的影响越小；尾水管处存在一定的低频脉动，这是由尾水管涡带引起。

图7为不同工况各部位压力脉动系数Cp的峰值柱状图。由图7可知，尾水管压力脉动系数峰值最小，在P=2 MW时出现最大值为0.78%；蜗壳压力脉动系数峰值在P=3 MW时出现最大值1.98%；整体来讲，无叶区的压力脉动系数为最大，且在P=3 MW时其压力脉动系数峰值出现最大值9.85%。从图7可以看出，无叶区的Cp峰值从P=1 MW到P=3 MW逐渐增大，在P=4 MW时明显减小，在P=5 MW时稍有增大；蜗壳进口处的Cp峰值变化规律与无叶区相同；尾水管出口处的Cp峰值从P=1 MW到P=2 MW时增大，在P=3 MW时减小，4 MW时增大，5 MW时又减小。造成上述变化的原因为，考虑到机组的水力稳定性，变转速寻优设置了最低单位转速启动运行线，水轮机启动工况及低负荷运行工况均可根据水头计算出对应的转速运行在该最低等单位转速线上。P为1、2、3 MW的3种工况均为低负荷运行工况，运行时都处于同一单位转速线上，其转速基本相同，因此当导叶开度逐步增大时，流量随之增大，压力脉动越来越剧烈；从P=4 MW开始，机组进入变速寻优状态，通过机组的单位流量确定其寻优后对应的单位转速，此时水泵水轮机运行状态相对稳定，因此无叶区及蜗壳处的压力脉动有所减小；P=5 MW时，机组流量继续增大，转速增大，各转轮叶道之间会产生均匀分布的涡结构，从而使得无叶区与蜗壳处压力脉动幅值稍有增加。

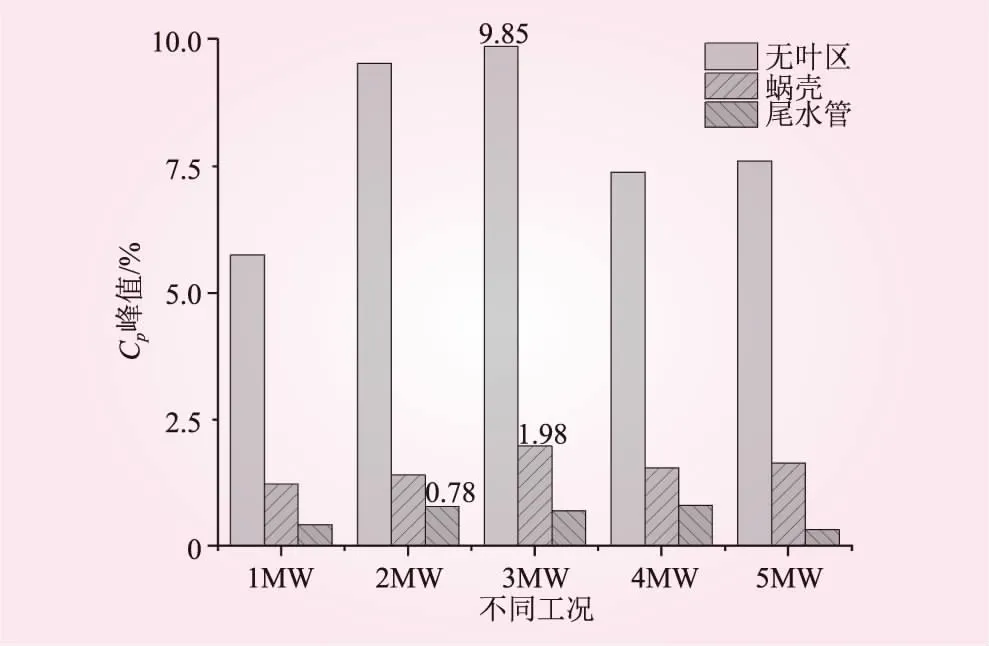
图7 不同部位各工况Cp峰值柱状图

由上述时域频域图及分析可以看出，经过变速寻优后的工况，无叶区压力脉动相较于寻优之前是有所减小的，且整个过程中压力脉动系数均10%以内，可以看出寻优变速运行对水机的内流稳定是有一定好处的。当工况发生变化时，可以通过在综合模型特性曲线上寻找在稳定条件下相应效率最高的工况点，这样既可以保证水机在不同工况下的稳定运行，又能提高其效率。

3 不同工况下水泵水轮机各部位压力脉动分析

选取不同工况下水泵水轮机相同部位的压力值进行压力脉动分析。将不同工况下同一部位的压力脉动特性放在一起进行比较，图8为各部位不同工况下压力脉动频域。由图8a可知，蜗壳进口处压力脉动的频率成分较为复杂，不仅受到转轮区域动静干涉的影响，还有许多其他频率的压力脉动。整体来讲，蜗壳仍是受动静干涉的影响最大。由图8可知，当P=1 MW时，蜗壳进口处主频为7fn，除了整数倍叶频14fn、21fn的压力脉动外，也有1.5fn及频率更低的压力脉动存在；当P=2 MW时，其主频仍为叶频7fn，次频为12fn，频率为14fn的压力脉动有一定增大，1.5fn及频率更低的压力脉动也存在；P=3 MW时，主频为叶频7fn，次频为12fn，14倍频和21倍频依然存在，但低频脉动幅值开始增大；P=4 MW时，低频脉动0.3fn成为蜗壳进口压力脉动的主频，次频为14fn，此外，频率为1.4fn及12fn的压力脉动也很显著；P=5 MW时，主频为12fn，次频为21fn，频率为1.2fn的压力脉动也仍较大。整体观察可知，蜗壳压力脉动还是一直受到转轮区域动静干涉的影响，除此之外，也存在其他频率的脉动，如低频脉动0.3fn，1～2倍频及12fn的压力脉动等。

图8 各部位在不同工况下压力脉动频域

由图8b可知，无叶区压力脉动主要受到动静干涉的影响，其5种工况主频均为叶频，次频均为2倍叶频。由图8b可知，无叶区压力脉动除整数倍叶频的频率外，也存在fn、2fn这样1倍2倍转频的压力脉动频率以及0.3fn的低频脉动。观察得知无叶区7fn的压力脉动幅值从P=1 MW到P=3 MW逐渐增大，在P=3 MW时达到最大值，在P=4 MW与P=5 MW时又有所减弱；而在14fn处的压力脉动幅值从P=1 MW到P=5 MW随着有功功率的增大而逐渐增大。

由图8c可知，尾水管出口处的压力脉动主要为低频脉动，由尾水管涡带引起。由图8c可知，当P=1 MW时，尾水管出口处主频为0.4fn，次频为23fn，除了0.4fn的压力脉动外，也有许多不同频率的低频脉动存在；当P=2 MW时，其主频为0.3fn，次频为24fn；P=3 MW时，主频为0.3fn，次频为25fn，此时还存在频率为叶频7fn的压力脉动；P=4 MW时，低频脉动0.3fn为尾水出口处的主频，且幅值陡增，次频为24fn；P=5 MW时，主频为12fn，次频为23fn，此时低频脉动幅值较前4种工况来说很小。整体观察可知，尾水管出口处压力脉动主要为低频脉动，几乎不受动静干涉的影响，低频脉动的幅值从P=1 MW到P=4 MW一直增大，且在P=4 MW处有一个突增达到最大值，在P=5 MW时又突降到最小，说明在P=4 MW时，尾水管涡带最为严重，造成了这一现象。

综合对比可知，P=3 MW和P=4 MW的工况较差，在这2个工况下，蜗壳进口、无叶区以及尾水管出口的低频压力脉动都有所升高，对机组稳定运行不利。P=3 MW为仍处于最低单位转速线上的工况，此时导叶开度增大，逐渐需要机组改变到相应的转速，P=4 MW时机组刚开始进行变速寻优，这2种工况均不属于非常稳定的工况，使得机组内部容易出现旋转失速、脱流及涡带等不利于水泵水轮机内部流态的状况，从而导致各部位的压力脉动更加剧烈。到P=5 MW时，机组处于较好的工况下，转速较高，导叶开度也与之匹配，因此可以发现此时的各部位压力脉动均有所下降。

除此之外，蜗壳进口处除了低频脉动与整数倍叶频的压力脉动外，频率为12倍频的压力脉动也非常显著，而在尾水管出口处，除了由尾水管涡带引起的低频脉动外，频率为23fn、24fn和25fn的压力脉动也很明显，这些频率的压力脉动可能是由于抽蓄机组各部位的固有频率、共振以及测量仪器影响等原因造成。

4 结 论

本文主要进行了水轮机工况下水泵水轮机在变速运行后稳定处于P=1～5 MW时的压力脉动时域及频域分析，从相同工况下水泵水轮机不同部位压力脉动分析以及同一部位不同工况下压力脉动的对比两个方面进行了比较和分析，最终得出以下几点结论：

(1)无叶区压力脉动最严重，主要由动静干涉引起，在无叶区由动静干涉引起的压力脉动产生后，它会随之向周围传递，蜗壳会受到其影响；尾水管距离动静干涉区域更远，受到的影响非常小，但尾水管会受到尾水管涡带的影响，产生低频压力脉动。

(2)从不同工况来讲，P=3 MW和P=4 MW的工况压力脉动较为剧烈，小流量工况水流在固定导叶内分布不均，随着水流向后延伸会导致转轮内部产生旋转失速现象，从而产生较大的压力脉动。大流量工况转轮叶片之间水流分布较为均匀，但是各转轮叶道之间会产生均匀分布的涡结构，从而使得无叶区产生较大的压力。

(3)由时域频域图可以看出，经过变速寻优后的工况，压力脉动情况良好，压力脉动系数在整个过程中均处于10%以内，变速机组的寻优运行路径使得水泵水轮机总是处于较好的工况点，变速运行有利于水泵水轮机内流流态等的改善。