降雨微分响应修正在港口湾水库洪水预报中的适用性分析
王玉丽,李京兵,张 峰,张锦堂
(1.安徽省水文局,安徽 合肥 230001;2.安徽水利水电职业技术学院资源与环境工程学院,安徽 合肥 230001)
水文模型的研究对象主要是时不变的离线系统,引起洪水预报误差的因素有很多,主要分为预报模型初始状态值误差、模型输入误差、模型结构误差以及模型参数非优化等[1],以上误差均会影响预报结果的精度,有效的误差修正技术会减少模型在预报时产生的误差,进一步提高预报精度。系统响应修正方法是一种结构简单、具有物理成因机理且不增加模型参数的实时洪水修正新方法,该方法的有效性、收敛性均已得到了证明[2-3]。
降雨资料作为洪水预报模型最重要的输入参数,雨量资料的误差是洪水预报模型误差的重要来源,其精度直接影响着预报结果的好坏[4]。本文在文献[5]、[6]研究的基础上,将降雨微分响应的误差修正方法应用于港口湾水库流域,从修正降雨量角度出发,将模型计算概化为一个系统,通过时段降雨引起的模型微分响应来修正降雨,进而修正出口断面的流量过程。本文将雨量单站微分响应修正与流域平均微分响应修正应用于港口湾水库流域,并比较2种模式修正效果的差异,探讨分析降雨微分响应修正方法在港口湾水库流域的适用性。
1 流域简介
港口湾水库是水阳江上游控制性工程,是一座以防洪为主,结合发电、灌溉、城市供水、水产养殖、旅游等综合利用的大(2)型水库。港口湾水库流域系皖南山区湿润地区,四季气候温和,雨量丰沛,多年平均降水量为1 583 mm,降水年际变化大,年内分配不均。多年平均气温为15.4℃,多年平均蒸发量为703 mm,其多年平均年径流量为9.62亿m3,流域植被覆盖率为75%[7]。由于流域坡降大、汇流快,所以洪水过程陡涨陡落。从流域的气象条件、下垫面条件和流量过程分析可知,该流域降雨径流关系具有蓄满产流的特点,可以按蓄满产流的理论和方法建立产流量预报方案。故选用降雨微分响应修正与三水源新安江模型[1]结合进行产汇流计算。
2 降雨误差微分响应估计方法介绍
基于“水文系统响应理论[2-3]”,将模型计算与实测之间的流量误差归结为降雨误差,只考虑模型输入变量中降雨因素的变化而引起的系统响应时,利用流域出口断面的流量信息,通过建立流量增量与降雨增量间的微分响应关系,计算时段面平均降雨引起的模型微分响应来对面平均降雨误差进行反演估计,将估计得到的面平均降雨过程重新代入到模型计算,进而达到修正出口断面流量过程的目的[8-9]。
Q(t)=f(P,t)
(1)
(2)
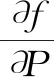
假设样本长度为L,P=[p1,p2,…,pL]表示降雨系列。流域出口断面的实测流量系列为Q=[q1,q2,…,qL]T,代入新安江模型计算得,计算流量系列为
QC=[qc1,qc2,…,qcL]T=[f(p1,p2,…,pL)]T
(3)
ΔQ=UΔP+E
(4)
式中,ΔP为需要通过微分响应估计求解面平均雨量误差,假设需要估计的面平均雨量长度为m,则ΔP=[Δp1,Δp2,…,Δpm]T;U为模型计算系统的微分响应。
结合式(3)和式(4),可知U的表达式为

(5)
式中,un为列向量,表示第n时刻的面平均降雨对应模型计算系统的微分响应。式(5)中的每一项均可以用差分近似求解
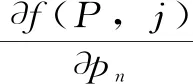
(6)
由于降雨量系列是随时间实时变化的,并且由式(6)可知,微分响应系列受其它时段的降雨量值影响,因此,降雨量pn所对应的微分响应系列也是动态变化的。
根据降雨径流形成过程可知,j-1时段出口断面的流量不会受到j时段降雨的影响。因此,j时段的降雨Pj产生的微分响应不会对j时段之前的流量值产生任何影响,即
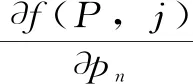
(7)
根据最小二乘估计原理,可得到第i+1步的降雨误差估计
ΔP=(UTU)-1UTΔQ+(UTU)-1UTE
(8)
因为E为白噪声向量,符合零均值分布的特点,所以
(UTU)-1UTE=0
(9)
因此,降雨误差微分响应最小二乘估计值为
ΔP=(UTU)-1UTΔQ
(10)
则新的降雨系列为
P=P+ΔP=[p1,p2,…,pL]T
(11)
其中流域平均微分响应与雨量单站微分响应的区别在于:计算微分响应U时,是否将流域内的所有雨量站当做一个整体或是个体考虑,若为前者,则为流域平均微分响应;若为后者,即为雨量单站微分响应。计算步骤[4-5]如下:
(1)P0是原始降雨系列,将其代入到新安江模型中计算,得到出口断面流量QC。

(4)根据式(8)计算得到第k+1步微分响应降雨误差估计为ΔP(k+1)=(U(k)TU(k))-1U(k)TΔQ(k)。
(5)根据式(11)计算第k+1步的降雨估计,即P(k+1)=P(k)+ΔP(k+1)。

3 港口湾水库流域应用
3.1 评价指标
选取港口湾水库流域1983年~2020年的23场次洪水资料,通过新安江模型计算与降雨微分响应修正,本次应用检验具体通过以下5项指标来衡量修正效果。
(1)相对径流深误差ΔR为
(12)
式中,Ro为实测径流深误差;Rc计算径流深误差。
(2)相对洪峰误差ΔQ为
(13)
式中,Qom为实测洪峰流量;Qcm为计算洪峰流量。
(3)确定性系数DC为
(14)
式中,Qoi为实测流量系列;QoA为实测流量均值;Qci为计算流量系列。
(4)洪峰滞时ΔT为
ΔT=To-Tc
(15)
式中,To为实测洪水峰现时间;Tc为计算洪水峰现时间。
(5)修正有效性系数REC为
(16)
式中,Qxzi为修正后的流量系列;REC表示修正的相对有效性,其值越大,说明修正方法的效果越明显,其最大值是1。
3.2 计算结果
本文选用港口湾水库流域1983年~2020年间23场洪水资料,分别进行新安江模型计算以及雨量单站降雨微分响应修正与流域平均降雨微分响应修正,其中新安江模型参数通过人机交互率定得到,且所有参数在计算和修正过程中保持不变。流域内雨量站主要有合庄、和阳、黄土坎、俞村、胡乐司、刘村、方塘、港口湾等8个雨量站,流域水系及雨量站点分布,如图1所示。
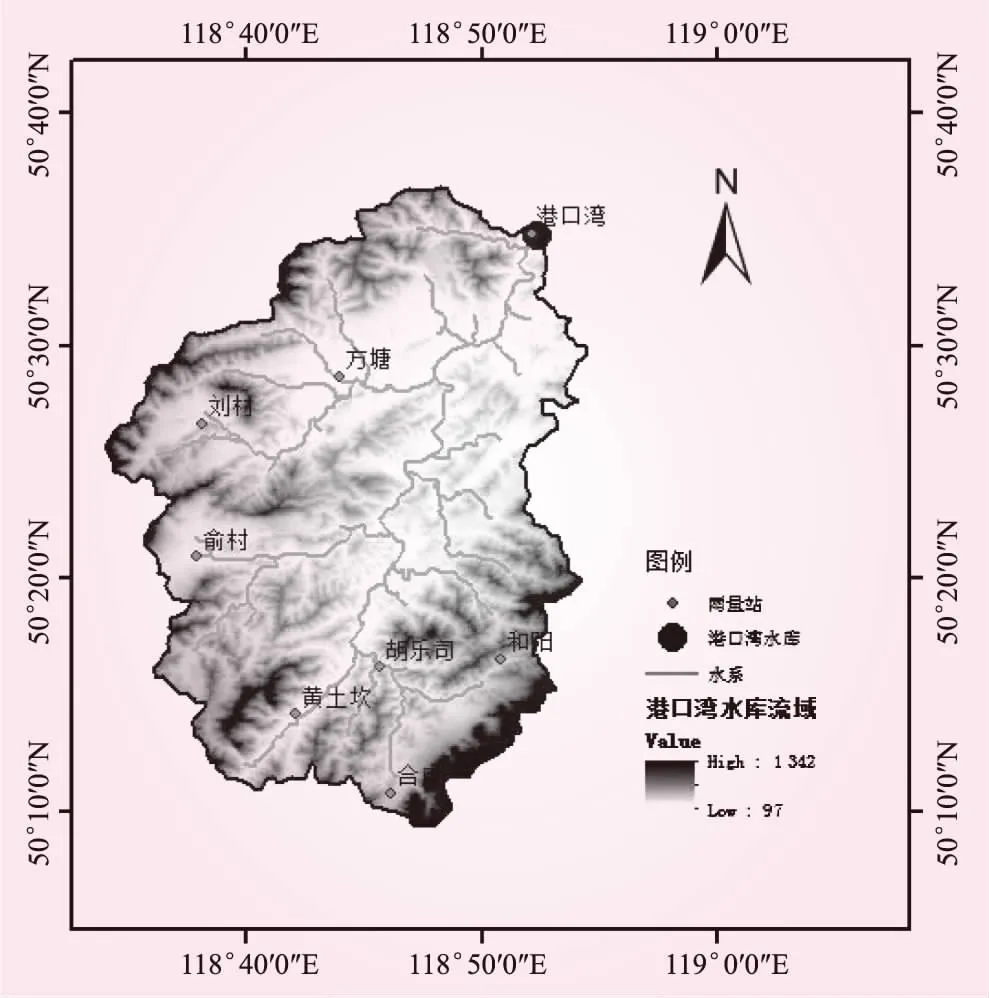
图1 港口湾水库流域水系及雨量站分布
港口湾流域23场洪水的新安江模型计算结果及单雨量站降雨微分响应修正与流域平均降雨微分响应修正结果,如表1所示。

表1 港口湾水库流域计算及降雨微分响应修正计算
基于以上2种模式降雨微分修正方法的计算结果,综合统计如表2所示。

表2 港口湾水库流域不同计算方法的评价指标统计
由于港口湾水库的出口断面入流量是由实测水位、出库流量和库容曲线反推而得到的,大多呈现锯齿波动过程,甚至出现降雨与流量过程不对应的现象,存在着异常误差,致使新安江模型计算结果精度评定整体不高。由表2可知,其中新安江模型洪量相对误差绝对值的平均值为11%,洪峰相对误差绝对值的平均值为12.09%,洪峰滞时绝对值的平均值为6.65 h,确定性系数为0.715。经过雨量单站微分响应修正后,洪量相对误差绝对值的平均值为10.01%,洪峰相对误差绝对值的平均值为7.38%,洪峰滞时绝对值的平均值为2.52 h,确定性系数为0.835。经过流域平均微分响应修正后,洪量相对误差绝对值的平均值为10.39%,洪峰相对误差绝对值的平均值为8.65%,洪峰滞时绝对值的平均值为0.74 h,确定性系数为0.801。
由表1、2可知,2种模式的降雨微分响应修正方法对于改进模型计算精度均是有效的,雨量单站微分响应修正的平均循环次数为8,流域平均微分响应修正的循环次数为18.5,雨量单站微分响应修正结果的精度较流域平均微分响应修正结果的精度高、效率快。经过降雨微分响应修正后的确定性系数整体大于模型计算的结果,其中有3场洪水联合修正后的确定系数小于模型的结果。
由表1可知,有3场次洪水的修正有效系数小于0,修正无效,其余20场次修正均有效。例如,由表1中20190810场次洪水计算及修正结果可知,该场次洪量、洪峰的计算结果与实测偏差大,相对误差均大于20%,经过流域平均微分响应修正和雨量单站微分响应修正后,确定性系数由0.846分别降到-0.453、-0.216,修正结果偏差较大,修正无效。以港口湾水库流域19840614、20190901场次洪水修正前后流量过程为例,如图2所示。由图2可知,19840614场次反推的入库流量过程无锯齿现象,而20190901场次反推的入库流量过程中锯齿现象较为明显,19840614场次的修正有效系数为0.774,20190901场次的修正有效系数为0.569,修正均有效,但19840614场次的修正效果较20190901场次明显。综上可知,实测资料的准确性及新安江模型计算结果精度对于降雨微分响应修正的效果存在一定的影响。但从整体而言,降雨微分响应修正适用于港口湾水库流域,并且效果明显。

图2 港口湾水库实际修正效果
4 结 语
(1)本文基于系统响应理论,单独考虑降雨误差所采用的降雨微分响应修正法,物理意义明确,在不损预见期的情况下,能够有效提升模型预报精度[2-3,8]。由计算结果表明,降雨微分响应在港口湾水库流域洪水预报中取得了较好的修正效果,其中洪峰、洪量相对误差及洪峰滞时得到不同幅度的减小,修正后精度提高;且2种模式的降雨微分响应修正的循环次数均较为合理。
(2)对比分析雨量单站微分响应与流域平均微分响应修正方法,在港口湾水库流域洪水预报中的应用效果有差别,但总体而言可行有效,可以应用于港口湾水库的洪水预报中,并值得进一步研究与推广。

