基于贝叶斯机器学习的大渡河上游岩石物理力学参数概率分布研究

邓 钦 宣, 张 韶 鹏, 邵 伟, 杨 洋

(1.四川足木足河流域水电开发有限公司,四川 成都 610041;2.四川大学水利水电学院,四川 成都 610200)

0 引 言

在水利水电工程中,大坝坝基及边坡稳定是保证水利水电工程安全至关重要的影响因素之一[1]。针对水利水电工程结构,《水利水电工程结构可靠度设计统一标准》[2]要求采用基于可靠度理论的分项系数设计方法进行结构设计,而可靠度设计要求提供岩石物理力学参数的分布信息。岩石在形成过程中经历了长时间跨度的复杂地质过程,岩体的材料和工程参数具有不同的分布特征且通常具有相关性,其联合分布具有复杂特征[3-4]。若各参数的联合概率分布估计不当,或者简单地忽略它们的相关性,会导致错估结构失效概率,导致有偏差的设计结果,从而直接影响工程安全[5-6]。

以准确估计岩石物理力学概率分布为目标,国内外诸多学者进行了大量研究,经历了从确定性分析到不确定性分析,从简单概率统计到概率分布拟合,从单参数边缘分布到多参数联合分布的研究历程,发展到了考虑不确定性的各参数不同边缘分布类型及不同相关结构的概率分布构建阶段[7-12]。然而,因岩石土体材料的场地或区域特异性、材料天然变异性和形成过程的复杂性,其联合分布常有悖于经典概率分布,且需要事先进行分布类型和相关结构的假设,而现有方法无法恰当解决该难题[13]。为此,本文将基于贝叶斯机器学习框架的高斯混合模型(Gaussian Mixture Model, GMM)应用于大渡河上游岩石物理力学参数概率分布构建任务中,在考虑统计不确定条件下精准刻画联合分布特征及各参数间的相关性,构建区域性多元岩石物理力学参数概率分布,为该区域的后续工程建设和设计提供参考。

1 高斯混合模型

高斯混合模型是混合分量为高斯分布的一种特殊混合模型,于1894年由生物统计学家Karl Person首次提出并应用于生物统计学中的偏态数据分析[14-15],并在之后的百年间获得了持续而深入的发展,已成为机器学习领域不可或缺的模型之一。高斯混合模型不仅具有极强的灵活性,而且继承了高斯分布的数学便利性,已被成功应用于多学科、多领域的研究,包括航空航天、医学、信号处理与分析、经济学以及社会科学等诸多方面[16]。

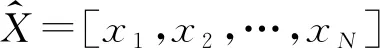
p(X|ω)=π1N(X|μ1,Σ1)+…+πkN(X|μk,Σk)+πKN(X|μK,ΣK)

(1)

一般形式为:

(2)

式中K为高斯分量的个数;N(X|μk,Σk)为1到K个高斯分量中第k个分量的概率密度函数;πk为第k个高斯分量的权重参数;向量π=[π1,…,πK]也被称为权重分布。为使GMM模型的概率密度函数在其定义域上积分为1,权重πk必须满足以下约束条件:

(3)

式中μk为第k个高斯分量的均值向量;Σk为第k个高斯分量的协方差矩阵,由各维度变量的方差和各变量之间的相关系数矩阵表示如下:

(4)

而在研究模型复杂度时,协方差矩阵Σk作为d(d+1)/2个参数进行计算。因此,多维高斯混合模型共有K(d+d(d+1)/2+1)-1个模型参数,模型参数求解涉及高维求解问题。为直观展示其参数规模,图1展示了不同变量维度条件下模型参数个数Np与高斯分量个数K的对应关系。

图1 不同变量维度条件下模型参数个数Np与高斯分量个数K的对应关系

由图1可知,高斯混合模型的模型参数个数Np随着高斯分量个数K的增加而线性增加,10维高斯混合分布在高斯分量个数为3时,即有高达198个参数。高斯模型复杂度在为概率分布拟合带来极大便利的同时,也给模型学习带来了挑战,因此,本文采用贝叶斯机器学习方法解决模型学习难题。

2 贝叶斯机器学习方法

除去上文提到的模型复杂度难题外,高斯混合模型的学习还因其为隐变量模型的特性存在标签切换问题,而在考虑不确定性分析的前提下,被广泛应用于求解GMM模型的EM算法失效[17]。因此,本节应用笔者之前提出的贝叶斯学习框架解决模型学习问题。

2.1 贝叶斯参数学习

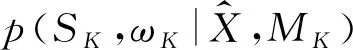
(5)

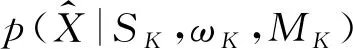
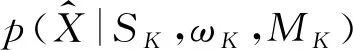
(6)

(7)

式中p(xi|Si,ωK,MK)为观测数据xi属于第Si个高斯分量的似然函数;p(Si|ωK,Mg)为在给定模型参数ωK和模型MK的情况下,观测数据xi属于第Si个高斯分量的概率。一旦隐变量SK被确定,则观测数据xi所归属的高斯分量即被确定。为定量描述观测数据xi的归属情况,引入变量nk,k= 1, 2, …,K,其代表了属于第k个高斯分量的观测数据样本的个数。

(8)

式中xi,k代表了属于第k个高斯分量的第i个观测数据;p(xi,k|μk,∑k为第i个观测数据归属于第k个高斯分量概率密度函数(PDF)值,可表示为:

(9)

GMM参数ωK(例如:π,μk, Σk,k= 1, 2, …,K)的共轭先验分布p(ωk|Mk)的设置如下[16-19]:

π～Dirichlet(α1,…,αk)

(10)

μk～N(bk,∑k/Bk)

(11)

(12)

式中 权重参数π= [π1,π2, …,πK] 服从狄利克雷分布(Dirichlet distribution),其概率密度函数PDF为:

(13)

式中a1,a2, …,aK为迪利克雷分布的分布参数。

均值参数μk的共轭先验分布为以bk为均值,∑k/Bk为方差的多维高斯分布,其中Bk为事先给定的比例因子。

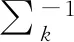
(14)

式中 Гd(·)为d维的Gamma函数,其表达式为:

(15)

在多维高斯分布的求解算法中,Wishart分布常被用来构造精度矩阵的共轭先验分布。概率密度函数表达式中Ck为Wishart分布的尺度参数,其为一个d×d的对称非奇异方阵。ck为Wishart分布的自由度参数,其与分布的自由度vk存在线性关系(即ck=vk/2)。

至此,表征GMM参数和隐变量的联合后验分布公式(5)的分子部分已经完全给出。但是,由于归一化常数仍然未知,仍旧无法得到参数和隐变量的后验分布样本。为了在考虑标签切换的前提下解决此问题,本文采用随机吉布斯抽样方法进行模型参数求解,此处不赘述。

2.2 贝叶斯模型比选

在应用数学模型进行数据分析建模时,模型不确定性是无法避免的,而对于高斯混合模型而言,其模型不确定性的最大来源就是高斯分量个数K的不确定性。确定高斯混合模型中的高斯分量个数会不可避免地涉及过拟合混合模型的学习问题,而由于标签切换和过拟合问题的存在,此时的高斯混合模型经常是不可识别的[18]。

随着计算科学的发展,科研工作者们提出了许多不同的模型选择方法来尝试考虑模型选择的不确定性。其中基于模型证据的贝叶斯模型比选方法同信息准则等方法比较具有优越性,因此,本文应用贝叶斯模型比选方法,权衡模型复杂度和拟合优度,选择最优备选模型。

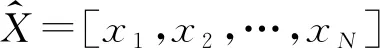
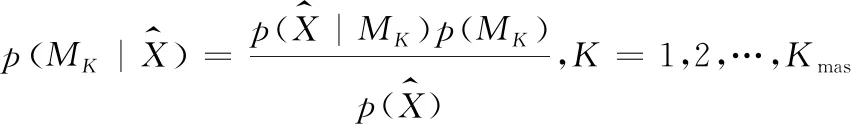
(16)

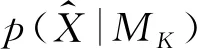
(17)

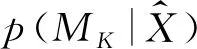
然而,当高斯分量个数大于1时,高斯混合模型的模型证据并没有解析解。在算法实践中,模型证据需要通过合适的后处理手段(postprocessing manner)求得。在后处理算法中,基于随机模拟方法的模型证据求解方法(Simulation-based approximations)的应用最为成功。本研究主要应用随机模拟方法中的桥采样(Bridge Sampling, BS)方法求解GMM的模型证据。

3 大渡河上游岩石物理力学参数概率分布构建

3.1 区域、数据概况

大渡河位于四川西部,是岷江水系最大的支流,年径流量470亿m3,干流全长1 062 km,天然落差4 175.0 m,为我国重要的水电能源基地之一。如今,大渡河干流形成了以下尔呷为龙头的28级开发方案,其中上游共规划有3级水电站,自上而下分别为下尔呷、巴拉和达维水电站,其中巴拉水电站在建,下尔呷、达维正处于项目前期阶段。

大渡河上游岩石主要以变质砂岩和板岩为主,巴拉水电站区域分布有花岗岩侵入区,本文收集了大渡河上游3级水电站的岩石物理力学参数试验数据,以岩体干密度ρd、饱和吸水率w、饱和抗压强度Rw为主要研究对象,考虑统计不确定性和参数相关性,通过所提方法构建大渡河上游岩石物理力学参数概率分布,验证所提方法有效性,为大渡河上游区域水电工程可靠度设计提供依据。大渡河上游岩石物理力学参数基本统计信息见表1。

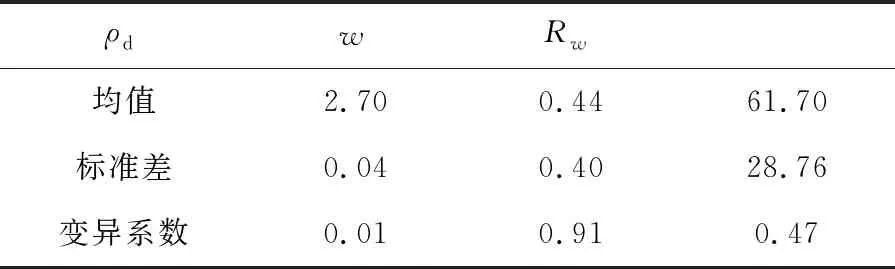
表1 大渡河上游岩石物理力学参数基本统计信息

如表1所示,所选的三个参数的统计特征之间存在较大差异,其中干密度ρd的分布较集中,变异系数仅为0.01,而饱和吸水率w及饱和抗压强度Rw的变异性较大,其中饱和吸水率的变异系数甚至高达0.91,这无疑为参数概率分布特征的准确表征带来了困难。

大渡河上游岩石物理力学参数试验数据的二维散点矩阵(图2),展示了各参数的频率统计直方图以及各参数之间的二维数据分布散点。

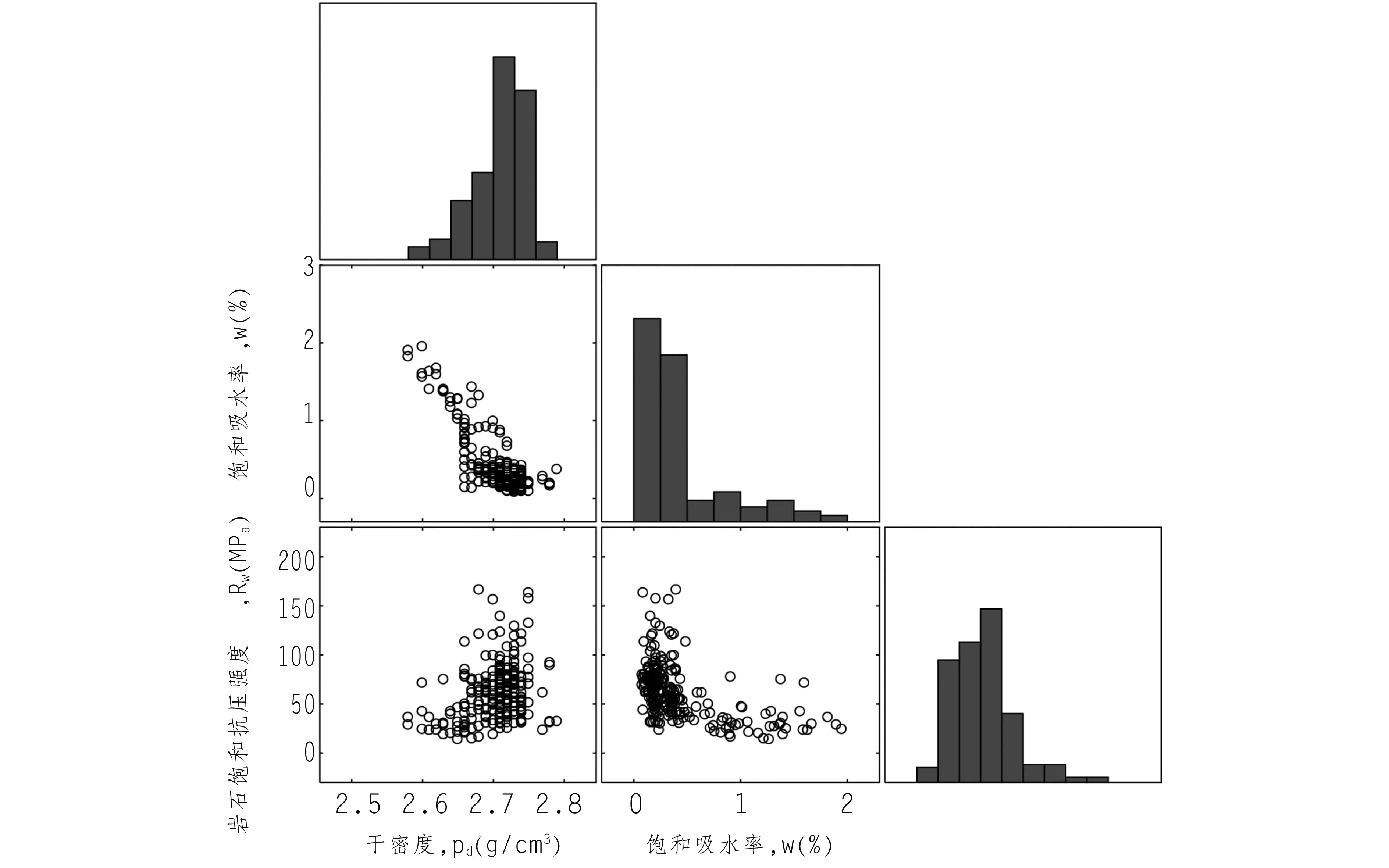
图2 大渡河上游岩石物理力学参数试验数据的二维散点图矩阵(n=222)

如图2所示,参数并不严格服从正态分布且具有多模态特征,且各参数之间明显具有非线性相关关系,很难通过现有的方法对这种复杂相关的特征进行描述。为了恰当表述岩石力学参数的多模态特征,同时处理参数之间的非线性相关关系,接下来应用所提方法对大渡河上游岩石物理力学参数试验数据进行分析。

3.2 GMM模型选择结果

首先假设共有5个备选模型M1,M2,M3,M4,M5,即高斯分量个数K的取值范围为从1到5的正整数(Kmax= 5),模型下标的数字即代表了其具有的高斯分量个数。备选模型的权重参数,各高斯分量的均值和精度矩阵的共轭先验分布,分别取为狄利克雷分布、正态分布和Wishart分布。然后应用RGS-GS方法学习高斯混合模型,设置RGS方法后验样本数、burn-in样本数和BS方法中的重要性抽样样本数均为10 000。

贝叶斯模型选择结果见图3。图中展示了5个备选模型的模型概率和模型证据的对数值,其中模型证据对数值用带有实心方形标记的实线表示,模型概率用直方图表示。由图3可知,随着模型分量个数的增加,模型证据的对数值在K= 4时达到最大值-489.08,之后下降至-489.68。因此,最优模型高斯分量个数为4的高斯混合模型GMM4,其对应的模型概率为0.59。

图3 贝叶斯模型选择结果

3.3 GMM建模结果

在进行最优模型结构进行选择后,应用所提贝叶斯学习框架对模型参数进行学习。图4(a)到(c)分别展示了各岩石力学参数的边缘概率分布拟合结果。

图4 各岩石力学参数的边缘概率分布拟合结果

图4中,黑色实线代表了PDF的最可能值,由黑色虚线围成的区域代表了PDF的95%置信区间,反映了模型统计不确定性的大小,直方图为归一化的频率分布直方图,展示了数据本身的分布特征及模型统计不确定性的大小。由图4可知,归一化的频率分布直方图分布于95%置信区间内,且与MPV值十分接近,这表明高斯混合模型GMM4的边缘概率分布不仅能很好地拟合观测数据的实际边缘分布特征,还能正确地表征其不确定性。

通过二维变量联合概率密度对数值等值线图,展示多维高斯混合模型对多维岩土体参数的联合分布的表征能力和对参数间相关性及相关结构的刻画能力,各岩石力学参数的联合概率分布拟合结果见图5。

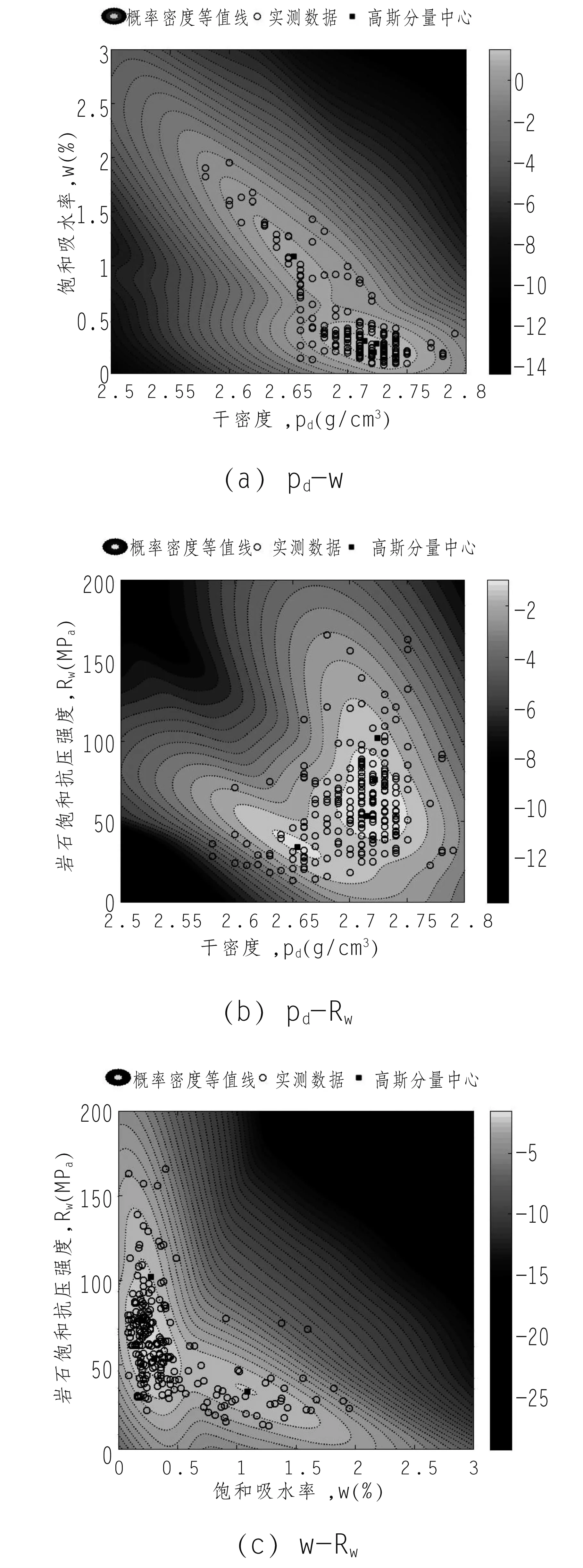
图5 各岩石力学参数的边缘概率分布拟合结果

图5展示了各变量间二维联合概率密度函数对数值的等值线图,图中用黑色空心圆形标记代表实测岩石物理力学参数数据;黑色实心正方形标记代表了识别出的各高斯分量的均值,也可认为是各高斯分量的中心;黑色虚线代表了各参数的联合概率密度对数值等值线,为增强结果的可视性,填充颜色从浅到深的演变对应概率密度函数对数值的从大到小变化。由各子图可知,观测样本点集中分布在颜色较浅的高概率密度区域,随着填充颜色从浅到深,观测样本点的分布密度也逐渐下降。此现象说明学习出的高斯混合模型能够有效刻画参数空间中的概率密度变化情况。各子图中的概率密度函数等值线并不是规则的椭圆形,而是呈现出随着数据点密度变化的不规则图形。这说明GMM模型表征的相关结构并不是高斯型或者其他传统类型的相关结构,而是由数据的特征决定的“数据驱动”相关结构,可以有效表述岩石物理力学参数分布特征。

GMM4的参数的最可能值如表2所示。

表2 GMM4参数最可能值

4 结 语

本文将基于贝叶斯机器学习框架的高斯混合模型应用于大渡河上游岩石物理力学参数概率分布构建任务中,在考虑统计不确定条件下精准刻画联合分布特征及各参数间相关性,构建了区域性多元岩石物理力学参数概率分布,得出以下结论:

(1)大渡河上游岩体干密度ρd、饱和吸水率w及饱和抗压强度Rw具有较大变异性,且分布具有多峰、多模态特征,具有复杂相关结构。

(2)所提方法和模型打破了现有方法必须事先假设各参数概率分布类型及相关结构类型的假设,能够在考虑统计不确定条件下精准刻画联合分布特征及各参数间相关性,有效表述了大渡河上游岩石物理力学参数分布特征。

(3)本文给出了所选参数联合概率分布的GMM模型,明确了模型参数,可直接用于后续工程设计工作,为后续工程提供了参考。