距离约束下的物流运输网络可靠性评估方法

徐秀珍，吴国林，牛义锋，陈思祁

重庆邮电大学 现代邮政学院，重庆 400065

物流运输网络是商品安全有效流通的重要基础设施，高效稳定的物流运输网络对社会和经济的发展至关重要[1-2]。在实际运作过程中，由于受不确定因素的影响，运输网络各条运输路线上的运输工具可能处于正常工作状态、部分失效状态、完全失效状态等多种状态。因此，各条运输线路的配送容量是随机的，从而导致整个运输网络的运输容量也是随机的。在理论研究中，物流运输网络可以看作由一系列点和边组成，其中，每个点可以代表需求地、供应地、转运中心或者配送中心等，每条边代表两点之间的物流活动[3]；并且，运输网络常常被建模为一个多态网络模型，网络中每条边具有相互独立的、有限的、取非负整数的随机容量。在多态网络模型下，运输网络可靠性是指，网络能够把一定数量的商品从供应地s配送到需求地t的概率。该可靠性指标是衡量网络在随机事件（恶劣天气、交通事故、车辆故障等）影响下能否持续提供高效、稳定物流配送服务能力的重要指标，在网络规划、设计与运营等方面越来越受到人们的关注与重视。

运输距离对物流运输网络的服务效率影响巨大，它不但决定了运输网络的规模大小而且影响着物流运输时间的长短，因此，运输距离是评估物流运输网络可靠性的重要因素与指标。例如，由于冷链商品保质期短、易损耗，运输距离需要控制在合适范围内，如果运输距离太长，会导致冷链商品质量受损，服务品质下降，最终给商家和消费者都会带来损失[4-6]。为此，本文关注运输距离约束的物流运输网络可靠性问题。

在多态网络模型下，Jane[7]提出了一个包括配送成本的可靠性指标Rd,b来评估配送网络服务能力，Rd,b表示网络能够把d单位的商品流从供应地s配送到需求地t，且总的配送成本不超过给定预算费用b的概率[8]。Niu等人[8]研究了计算Rd,b的极小容量向量（简称(d,b)-极小路）方法，并构建了求解(d,b)-极小路的改进数学模型。在传统(d,b)-极小路模型的基础上，Xu 等人[9]最近提出了新的(d,b)-极小路求解模型，并提出了一种高效的重复(d,b)-极小路识别方法。在考虑运输损耗的基础上，Lin等人[3]将配送网络可靠性定义为网络输送到目的地的完整商品数量能够满足市场需求，且总的配送成本不超过给定预算费用的概率，并且提出了一种计算该可靠性指标的方法。

此外，也有学者从满意度角度出发对物流配送网络可靠性进行了研究。尹小庆等人[7]将行程时间可靠性作为满意度评价指标，构建了城市冷链末端配送站点选址模型。谢婷[8]将托运货物到达时间是否满足要求作为时间满意度的评判标准，将货物运输时间满意度与运输时间可靠度作为主要约束条件，以运输总成本最小为优化目标，建立了多式联运网络优化模型。Lin等人[9]将商品运输时间和中途停留次数引入满意度评价，构建了多状态配送网络可靠性评估模型和方法。注意到现有研究在可靠性分析中没有考虑运输距离约束问题，而运输距离对物流运输网络的服务效率影响巨大，不仅决定运输网络的规模大小而且影响物流运输时间的长短。因此，运输距离是评估物流运输网络可靠性的重要因素与指标。以冷链物流为例，由于冷链商品保质期短、易损耗，运输距离需要控制在合适范围内，如果运输距离太长，会导致冷链商品质量受损，服务品质下降，最终给商家和消费者都会带来损失[10-12]。为此，本文关注距离约束的物流运输网络可靠性问题。

目前，针对距离约束的网络可靠性研究大多集中于二态网络（边只有连通和不连通两种工作状态），其定义为网络存在一条距离不超过给定上限的通路的概率[10-11]。注意到二态网络模型只考虑两种极端状态，不适用于物流运输网络可靠性分析[12-13]。Zhang 等人[6]首先研究了距离约束的多态网络可靠性问题，并提出了可靠性评估算法。该算法首先利用距离约束判定并删除冗余边，然后寻找网络所有的d-极小路，最后，将d-极小路代入容斥定理公式计算可靠性。需要指出的是，Zhang等人提出的算法只考虑将冗余边删除，而忽略了不存在冗余边的网络中仍然可能存在不满足距离约束的d-极小路，导致计算结果出现错误。

为了精准评估物流运输网络的服务效率，本文考虑运输距离约束的物流运输网络可靠性指标，计算该可靠性指标的关键是求解运输距离约束下的d-极小路问题。为了克服现有方法的缺陷，在确定网络冗余边的基础上，本文构建了运输距离约束下的d-极小路数学模型，并提出运输距离约束下的物流运输网络可靠性评估方法。最后，本文将提出的可靠性指标和评估方法应用于物流运输网络可靠性分析。结果表明，距离约束的网络可靠性指标能够更加精准评估物流运输网络的服务水平，从而为管理者在物流配送网络优化设计方面提供决策指导。

1 网络模型及预备知识

1.1 网络模型

本文将物流运输网络看做一个无圈有向网络，并用G(N,A,W)表示，其中，N={s,1,2,…,n,t}表示节点集，A={ai|1 ≤i≤m} 表示运输边的集合，W=(W1,W2,…,Wm)表示各运输边最大运输能力组成的容量向量，也称作最大容量向量。在网络中，极小路代表一条从s到t的路径，且不包含有向圈。令P={P1,P2,…,Pp}表示网络中所有极小路组成的集合，其中Pi是第i条极小路，p是极小路的总数量。受随机事件的影响，各条运输边可能会有不同的容量状态。因此，用xi表示边ai的一种容量状态，其中0 ≤xi≤Wi；并且，用X=(x1,x2,…,xm) 表示容量向量，表明各条边所处的容量状态。其中网络G各边容量状态如表1所示。

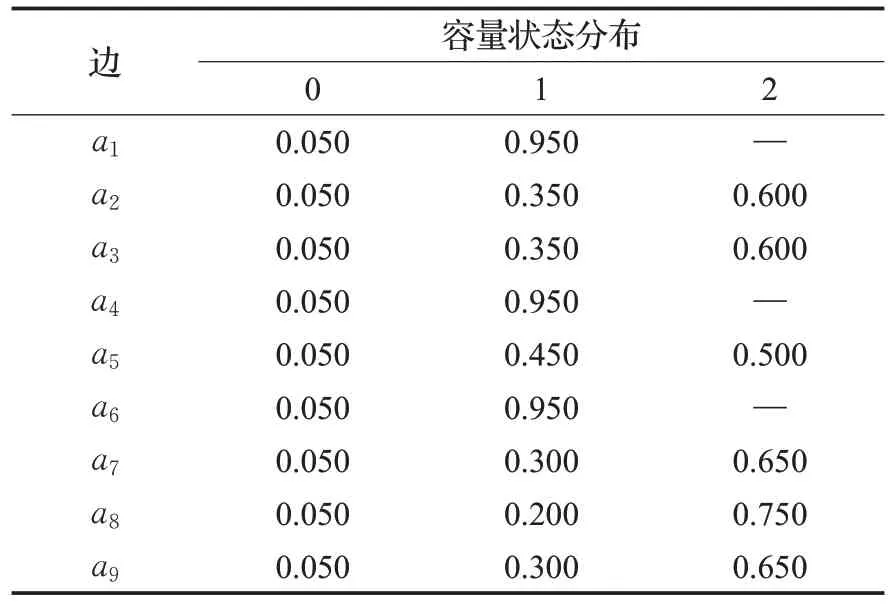
表1 图G各边的容量数据Table 1 Capacity data for each edge in network G

鉴于本文所讨论的网络为无圈有向网络，本文将极小路也称作st-路径，此外，将st-路径包含的边的数量称为该st-路径或极小路的长度，记为L(Pj)(1 ≤j≤p)，disG－a(u,v)表示包含有向边a=(u,v)的最短路径的长度（不包括边a的长度），本文的网络模型满足以下假设条件：（1）每个点都完全可靠；（2）各边的容量状态是一个随机变量，且服从给定的概率分布；（3）不同边的容量状态在统计上是相互独立的；（4）网络中的流满足流守恒定律。如图1 所示的多态网络G中st-路径集合P={P1,P2,…,P6}，p=|P|=6，st-路径的长度L(Pj)(1 ≤j≤6)如表2所示。

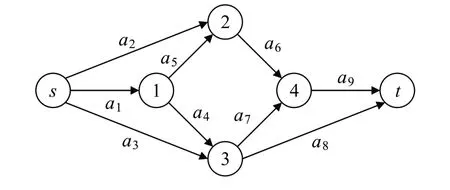
图1 网络GFig.1 Network G

表2 图G中st-路径Table 2 st-paths in network G

1.2 预备知识

给定网络G(N,A,W)，传统的网络可靠性Rst(G,d)是指网络能够把d单位的需求从供应地s运输到需求地t的概率[14-16]，其中d也称需求水平。计算Rst(G,d)最常用的方法是利用满足需求水平d的极小容量向量，简称d-极小路，Lin 等人[17]最先提出求解d-极小路的数学模型，现有研究也大多采用该模型。令fj(1 ≤j≤p)代表第j条st-路径中的流量，所有fj(1 ≤j≤p)组成的向量称为可行流向量，记作F=(f1,f2,…,fp)，则Lin 等人[17]的模型由引理1给出。

引理1 在无圈有向网络G中，容量向量X=(x1,x2,…,xm)是d-极小路，当且仅当下面的条件成立：

其中，CPj=min{Wi|ai∈Pj}是第j条st-路径的最大容量。引理1 中，约束条件（1）保证网络的最大需求水平为d，约束条件（2）保证通过每条st-路径上的流量低于该路径的容量限制，约束条件（3）指出边的容量状态与通过该边的网络流之间的关系。当找到网络所有的d-极小路，Rst(G,d)可以利用不交和方法[18-19]来计算。给出该方法之前，容量向量的比较运算阐明如下。

定义1 给定两个容量向量X=(x1,x2,…,xm)和Y=(y1,y2,…,ym)，X≥Y是指对于i=1,2,…,m都有xi≥yi成立；X＞Y是指X≥Y且至少存在一个i使得xi＞yi成立。

假设网络所有的d-极小路为X1,X2,…,Xθ，令Φ1={X|X≥X1} ，Φ2={X|X≥X2},…,Φθ={X|X≥Xθ} ，则 利用不交和算法可计算Rst(G,d)如下[20]：

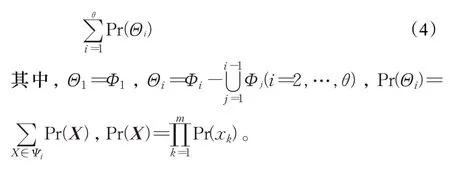
2 距离约束下的网络可靠性计算

2.1 距离约束下的网络可靠性

对于给定的需求水平d和距离约束D，距离约束下的网络可靠性Rst(G,D,d)是指网络能够将d单位的需求从供应地s运输到需求地t，且运输距离不超过D的概率，其中，运输距离等于流量大于0 的st-路径的最大长度。根据Rst(G,D,d)的定义易知，如果网络中某条边只出现在长度大于D的st-路径中，则这条边对可靠性没有任何贡献，称这样的边为冗余边。

定义2 在网络G中，如果边ai只包含在长度大于D的st-路径中，则称ai是冗余边。

例如，给定D=3，图1 中的边a5只出现在st-路径P1={a1,a5,a6,a9}中，且该条st-路径的长度为4，因此，a5为冗余边。检测冗余边的方法由下面的引理给出。

引理2[6]如果disG－a(s,u)+disG－a(v,t)≥D，则边a是冗余边。

如果网络在X下能够将d单位的需求从供应地s运输到需求地t，且所有流量大于0的st-路径的长度不超过D，则称X为合格容量向量。因此，根据定义可知Rst(G,D,d)=Pr{X|X为合格容量向量}。为了更高效地计算Rst(G,D,d)，Zhang等人[6]提出首先应检测并删除冗余边；然后再利用引理1 求解d-极小路；特别地，Zhang等人[6]认为不存在冗余边的网络的d-极小路全部是合格容量向量，于是将d-极小路代入公式（4）计算Rst(G,D,d)。但需要指出的是，不存在冗余边的网络的d-极小路不一定满足距离约束，因此，不一定是合格容量向量。以图1中的网络G为例，假设D=3，d=2，冗余边a5被删去后的化简网络G*如图2 所示。根据定义2 可知G*中不存在冗余边，但对于2-极小路X=（1，1，0，1，1，1，0，2）来说，极小路P3={a1,a4,a7,a9}运输的流量f3=1 且L(P3)=4 ＞D。

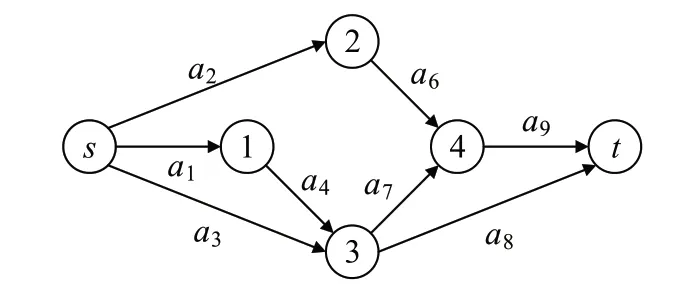
图2 化简后的网络G*Fig.2 Simplified network G*

2.2 距离约束下的d-极小路模型

前面已经指出，不存在冗余边的网络仍然可能存在长度大于D的st-路径，从而无法保证化简后的网络的d-极小路全部是合格容量向量。为了保证所有d-极小路满足距离约束，可以将长度大于D的st-路径的流量设置为0。基于此，在构建d-极小路模型时，应首先对st-路径按照长度大小进行升序排列，假定L(P1)≤L(P2)≤…≤L(Pg)≤L(Pg+1)≤…≤L(Pp)，其中L(Pg+1)＞D且L(Pg)≤D，将长度大于D的st-路径上的流量设置为0（即不参与流的输送），则满足距离约束D的候选d-极小路模型由下面的定理给出。

定理1 在无圈有向网络G中，假定L(P1)≤L(P2)≤…≤L(Pg)≤L(Pg+1)≤…≤L(Pp),L(Pg+1)＞D，L(Pg)≤D，容量向量X=(x1,x2,…,xm)为满足距离约束D的d-极小路当且仅当下面的条件成立：

需要注意的是，在引理1中，j的取值范围为1 ≤j≤p，但是在约束条件（5）中，j的取值范围为1 ≤j≤g，其中，g≤p。

2.3 算法

下面给出一种计算Rst(G,D,d)的算法，该算法首先求解满足距离约束的d-极小路，然后根据公式（4）计算可靠性值，具体步骤如下：

输入：网络G(N,A,W)，需求水平d，距离约束D。

输出：可靠性Rst(G,D,d)。

步骤1 利用引理2检测并删除G中的所有冗余边，得到网络G*(N*,A*,W*)。

步骤2 利用现有算法（文献[17]中的算法）搜索网络G*(N*,A*,W*)的所有st-路径。

步骤3 计算所有st-路径的长度，并按照长度大小 进行 升序排列，假 定L(P1)≤L(P2)≤…≤L(Pg)≤L(Pg+1)≤…≤L(Pp),L(Pg+1)＞D且L(Pg)≤D。

步骤4 利用2.2节定理1求解所有d-极小路。

步骤5 利用公式（4）计算Rst(G,D,d)。

下面分析算法每一步的时间复杂度：步骤1可以利用经典的Dijkstra 算法求解，需要O(m(m+nlogn))[6]时间。找出网络中所有st-路径需要O(λp*)[17]，λ为st-路径的平均长度，p*为无冗余边网络中极小路的数量。步骤3 需要O(p*(m*+logp*)) 时间。根据Forghanielahabad and Bonani等人[18]提出的最新算法求解定理1中的模型需要O(m*gθ)时间，其中m*为网络G*(N*,A*,W*)中边的数量，g为化简网络中满足直径约束的st-路径数量，θ为定理1求得的所有d-极小路数量。步骤5 中利用不交和算法计算Rst(G,D,d) 需要时间。注意到，该算法复杂程度与距离约束D有关，若网络中所有st-路径的长度都不大于距离约束，则算法求得无距离约束的网络可靠性值。

2.4 算例

考虑图3所示多态网络H，其中，N={s,1,2,3,4,t}，n=4。边集A=(a1,a2,…,a10)，m=|A|=10。为方便计算，现假设边ai(1 ≤i≤10)的容量状态为0，1，2，状态概率分别为0.03，0.07，0.90，距离约束D=3，需求点t的需求为d=5。现用提出的算法计算Rst(H,3,5)。

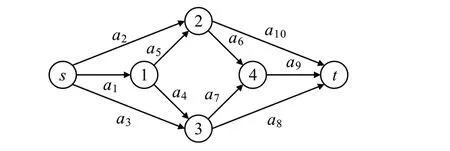
图3 算例网络HFig.3 Example network H

步骤1 计 算Dis(ak)=disG－a(s,u)+disG－a(v,t) 。得Dis(a1)=2，Dis(a2)=1，Dis(a3)=1，Dis(a4)=2，Dis(a5)=2，Dis(a6)=2，Dis(a7)=2，Dis(a8)=1，Dis(a9)=2，Dis(a10)=1。判断Dis(ak)≥3？判断得，D=3 时网络图H中不存在冗余边。输出新网络图H*(N*,A*,W*)。其中，N*={s,1,2,3,4,t} ，n=4 ，边集A*=(a1,a2,…,a10)，m=|A|=10。

步骤2 网络图H*(N*,A*,W*)中所有的st-路径为P1=(a2,a10)，P2=(a1,a5,a10)，P3=(a2,a6,a9)，P4=(a1,a5,a6,a9) ，P5=(a1,a4,a8) ，P6=(a3,a7,a9) ，P7=(a1,a4,a7,a9)，P8=(a3,a8)。

步骤3 步骤2 中st-路径长度分别为L(P1)=2 ，L(P2)=3，L(P3)=3，L(P4)=4 ，L(P5)=3，L(P6)=3，L(P7)=4 ，L(P8)=2 ，排 序 得L(P1)≤L(P8)≤L(P2)≤L(P3)≤L(P5)≤L(P6)≤D＜L(P4)≤L(P7)。其中L(P4)＞D和L(P7)＞D。

步骤4 所有满足定理的5-极小路为X1=（1，2，2，1，0，1，2，0，2，1），X2=（2，1，2，2，0，1，2，0，2，1），X3=（2，2，1，1，1，1，2，0，2，1），X4=（1，2，2，0，1，0，2，1，2，1），X5=（2，1，2，1，1，0，2，1，2，1），X6=（2，2，1，0，2，0，2，1，2，1），X7=（2，2，1，2，0，2，2，0，1，2），X8=（1，2，2，1，0，1，2，1，1，2），X9=（2，1，2，2，0，1，2，1，1，2），X10=（2，2，1，1，1，1，0，0，2，2），X11=（1，2，2，0，1，0，2，2，1，2），X12=（2，1，2，1，1，0，2，2，1，2），X13=（1，2，2，1，0，2，1，0，2，2），X14=（2，2，1，1，1，2，1，0，2，2），X15=（1，2，2，0，1，1，1，1，2，2），X16=（2，1，2，1，1，1，1，1，2，2），X17=（2，2，1，0，2，1，1，1，2，2），X18=（2，1，2，0，2，0，1，2，2，2）。

步骤5 利用不交和方法求得D=3，d=5 时网络可靠性为Rst(H,3,5)=0.803 005。

注意到，当D=3 时，本文算法中共有6条st-路径参与流量分配，最后求得18个5-极小路；而Zhang等人[6]的算法利用8条极小路去分配流量，最后产生了20个5-极小路。二者数量不同是因为Zhang等人[6]的算法只考虑了冗余边的删除，没有考虑到删除冗余边后的网络仍可能存在不满足距离约束的st-路径。在本例中，删除后的网络仍有2 条st-路径并不满足距离约束D=3，这就导致5-极小路的计算错误。

3 实际案例分析

本章将提出的算法应用于物流运输网络可靠性分析。图4 所示的网络是关于A、B 两城市之间的一个物流运输网络，该网络引自文献[19]，包含13个节点、22条边。网络中各边ai(1 ≤i≤22)的容量状态如表3 所示。在数值分析中，提出的算法用MATLAB 程序语言实现。表4列出了计算可靠性所消耗的CPU时间，数值计算的结果如表4、表5 所示（注意到max(L(Pj))=9，因此，D=9 时等同于没有距离约束），包括不同距离约束下的冗余边数量、st-路径数量，满足距离约束的st-路径数量，CPU 时间，以及网络可靠性等；为了便于比较，图5展示了在需求水平d保持不变时，距离约束对可靠性产生的影响。根据表4、表5、图5的结果可以看出：

图4 一个物流运输网络Fig.4 Logistics transportation network

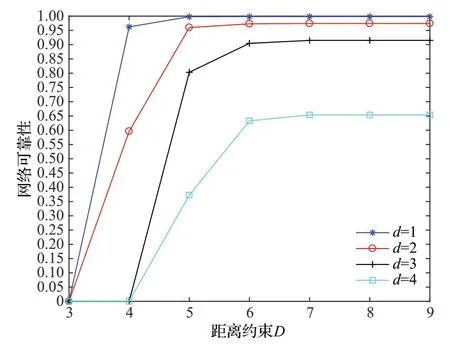
图5 不同距离约束下的网络可靠性Fig.5 Reliabilities under different distance constraints

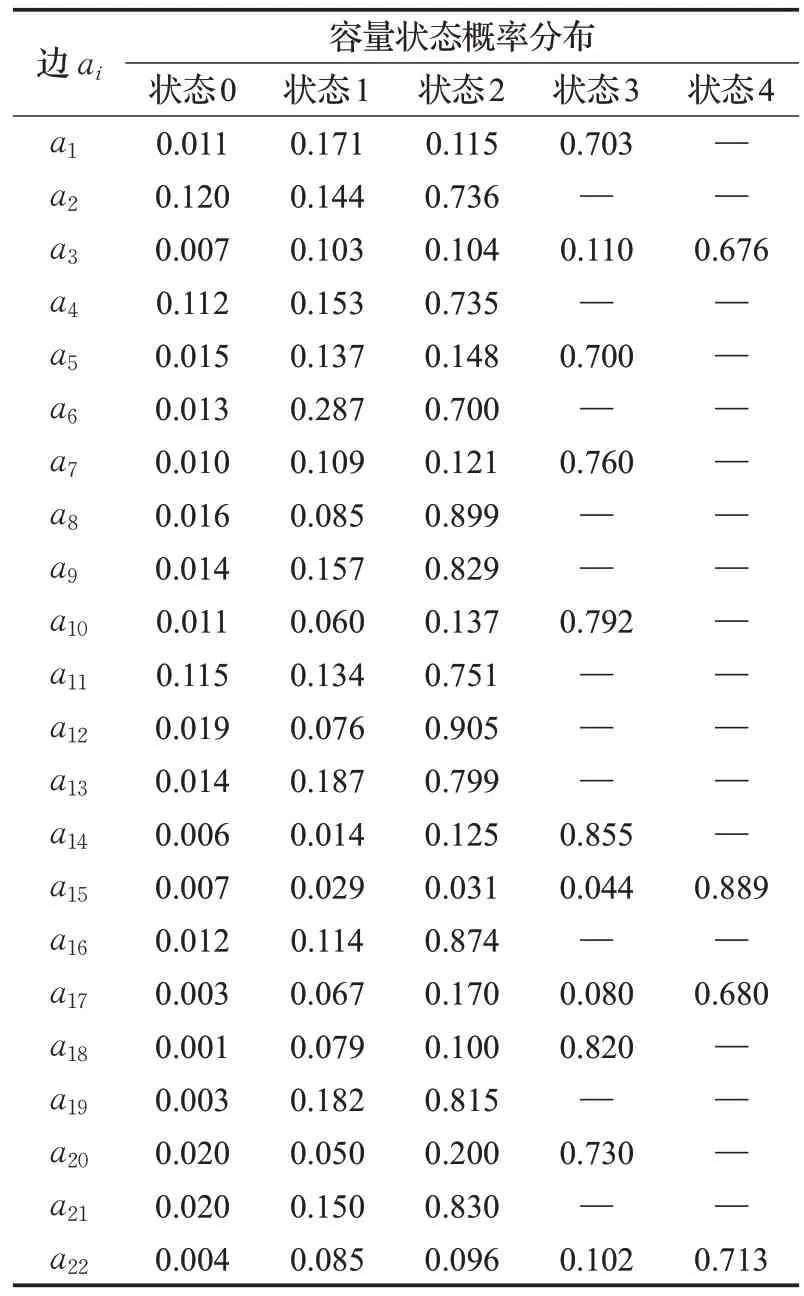
表3 图4网络各条边的容量状态Table 3 Capacity data for each edge in Fig.4

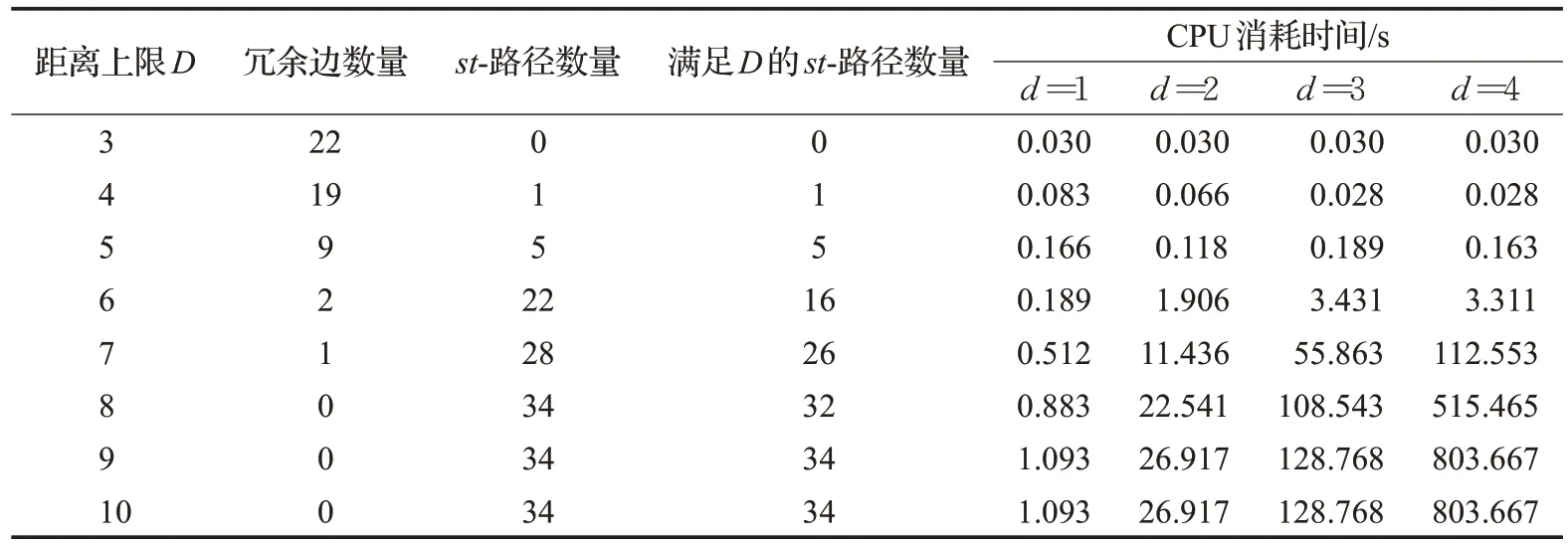
表4 CPU时间Table 4 CPU time

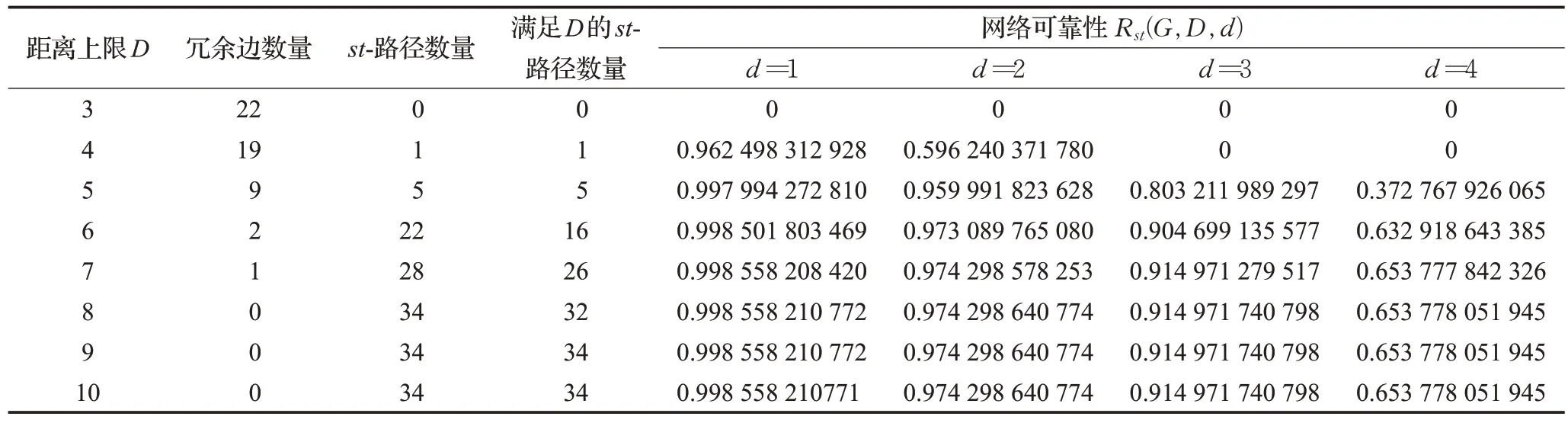
表5 数值计算结果Table 5 Numerical results

（1）保持距离约束D不变，当5 ≤D≤10 时，随着网络需求水平d的增加，网络可靠性下降，算法的运行时间呈增加趋势。但当D=3 时，因为网络中不存在满足距离约束的st-路径，也不存在满足距离约束的d-极小路，网络的可靠性为0，此时CPU 时间为计算st-路径花费的时间。当D=4 时，删去冗余边后的网络只有一条st-路径，当d=1 或2 时，对应的可靠性分别为0.962 498 312 928 和0.596 240 371 78，但当d＞2 时，因为该st-路径的最大容量为2，所以网络可靠性为0。

（2）注意到当网络中不存在冗余边时，仍有可能存在不满足距离约束D的st-路径。比如，距离约束D=6或7 或8 时，删去冗余边的网络中仍然存在不满足距离约束的st-路径。因此，需要利用定理1求解满足距离约束的所有d-极小路。

（3）在网络中，距离约束D取值的变化影响着st-路径的数量，进而对d-极小路的数量和网络可靠性值产生影响。注意到在某个区间范围内，不同的D值对应不同的可靠性值，其中，当D≥max(L(Pj))=9 时，Rst(G,D,d) 等于无距离约束下的可靠性Rst(G,d) ；当D＜min(L(Pj))=4 时，网络中不存在满足距离要求的st-路径，所以Rst(G,D,d)=0。

（4）当距离约束D在某个区间范围变化时，网络可以保持较为稳定的可靠性。譬如，对于图4 所示网络，当D的取值从9 减少为7 时，无论需求水平d取何值，Rst(G,D,d)与无距离约束的可靠性Rst(G,d)并无太大差别，此时，不同需求水平下网络可靠性最大变化率不足0.01‰。此外，当d=1，2，3，4时，可靠性计算时间分别节约了0.21 s、4.36 s、72.905 s、691.114 s。这说明对于某些需求水平来说，利用距离约束可以减少可靠性计算时间，同时获得比较准确的可靠性值。

（5）值得注意的是，删去冗余边后的网络虽然只包含很少的st路径，但仍能够保持较高的可靠性水平。譬如，当D=4，d=1 时，网络只存在一条st-路径（该路径由4 条边，5 个节点组成），但此时网络的可靠性水平仍高达0.962 498，即Rst(G,4,1) =0.962 498。这说明，从供应地s配送到需求地t传输d单位需求流量，运输距离较短的配送路径对网络可靠性具有重要影响。

综上，本文提出的可靠性评估方法克服了现有算法的缺陷，且数值结果表明，合理的运输距离约束不会对物流运输网络可靠性产生较大影响，但能够提升可靠性的计算效率；需求水平也同样影响着距离约束下的网络可靠性，当需求水平越接近于运输网络的最大承载量时，网络可靠性下降越大；较短st-路径对网络可靠性有显著影响。因此，管理者在物流运输网络运营过程中，应合理平衡配送距离、承载容量、可靠性之间的关系。

4 结语

运输距离对物流运输网络服务质量有重要影响，本文聚焦距离约束下的物流运输网络可靠性，并提出有效的评估方法。该可靠性评估方法仍然属于两阶段方法，第一阶段求解满足距离约束的d-极小路，第二阶段利用不交和算法计算可靠性值。为了求解满足距离约束的d-极小路，在确定网络冗余边的基础上，本文构建了距离约束下的d-极小路数学模型。最后，通过数值实验对所提出的可靠性评估方法的有效性进行了验证，并分析了运输距离约束对网络可靠性的影响。注意到运输损耗在物流运输网络中是一个普遍现象，后续研究考虑将运输损耗和运输距离同时纳入可靠性分析中，建立合适的可靠性指标，并提出有效的评估方法。