基于数据驱动优化的火电发电机组调峰调频方法研究
李 扬,杨 鹏,吕瑞瑞
(青岛大学 计算机科学与技术学院,山东 青岛)
引言
火电是人为参与度最高、最适合调配的电能形式。在调峰调频工作领域,德国[1]和美国[2]AGC 调频服务主要由燃气、水电以及火电等机组协作提供。牛玉广[3]等通过改进多目标进化算法、基于HKA 优化算法模糊增益调度、基于自适应遗传算法以及基于卡尔曼进化算法设计方案。陈彦桥[4]根据单元机组机炉协调控制系统的T-S模糊模型设计了PDC控制算法。林金星[5]等提出了一种新的免疫优化模糊增益调度H∞鲁棒控制方法。郝莹[6]进行控制逻辑的分析确定控制器参数选择和控制器结构。Georgi M.Dimirovski[7]提出一种分散式自适应协调控制器设计。在评价标准方面,Henderson P.D.[8]给出调峰调频运营成本的一般概述,南方电网调峰调频发电公司[9]制定的技术监督标准实现全过程监督。本文提出了针对火电机组调峰调频的多目标优化算法并进行对比校验。
1 模型建立以及过程分析
1.1 预处理和建模分析
为了进一步贴近模型现实情况,本文使用实际工况运行数据对控制参数进行优化。由于现实工况下传感器的运转、数据采集存在误差,例如断点、时间间隔不一致,对应时间点不同等。为了解决这些问题,采用server 和tagname 对所有文件的行进行合并,并运用LOF 和kmeans 方法来去除离群点和离散点。
1.2 优化模型
1.2.1 整体模型
为了深入研究火电机组的运行过程,将火电机组模型进行了分解,将模型阶段的输出作为下一个模型的输入,从而更好地优化其运行。通过建立不同模型的联系,可以全面考虑火电机组不同阶段的影响因素,为最终的优化提供有效参考。

图1 发电机组控制整体模型
1.2.2 建模选择
在进行火电机组的调峰调频时,为了综合考虑火电机组的现实运转情况,本文采用了对磨煤系统、锅炉系统、转子运行等模型过程的分块合并的方法。
1.2.2.1 磨煤制粉系统建模 当接收到煤粉操作指令时,磨煤机的输出包括煤粉产量和传输口风速等,导致这个过程表现出延迟特性。一旦接收到调整煤粉操作指令,磨煤机通过控制转速、调整进气、调整煤量以及传输口风速,会产生二次风量、旁路风量以及煤粉浓度,同样表现为纯延迟特性。
1.2.2.2 锅炉燃烧室建模 在锅炉燃烧室,磨煤制粉系统的煤粉作为燃料和空气混合产生热量,锅炉加入预热水产生蒸汽,这一阶段我们通过控制烟气烧摆角和阀门开度来进行调控,输出为蒸汽压力和汽包压力等,由于燃烧器的摆角角度决定了燃烧炉内的燃烧情况以及输出烟气温度,摆角变大,燃烧更充分,炉内温度会较高,燃烧器的摆角指令可以看作是纯延迟的一阶惯性环节,摆角角度对于热量和烟气通道内换热量都有影响。锅炉产生的热量和蒸汽近似为线性关系:
蒸汽的流速以及压强与烟气换热量的关系为:
1.2.2.3 转子模型 转子是汽轮机组的主要部件,流入汽轮机的蒸汽推动叶片旋转做功产生机械能。转子的力矩平衡方程和功率平衡方程为:
式中,T 为蒸汽提供的动力;L 为负载力;f 为摩擦力。
蒸汽转矩TT可通过动叶片的速度三角形求得。简化为根据前后参数确定前后蒸汽焓降,然后再乘以蒸汽流量QZ、Qg,得到功率N(千瓦),再根据公式(7)求得转矩:
式中,NT为蒸汽转矩(牛米);N 为功率(千瓦);n 为转速(转/分)。
1.2.2.4 单机无穷大系统模型 转子在磁场中转动发电后,并入电网送电,由于本文只研究单个汽轮机的运转情况,相比较于全部的机组来说,建立了一种单机无穷大的电网模型来研究供电可以减少在实际运转过程中外部电网对机组本身产生的影响,发电机功率方程:
式中,ΔPe为阻尼功率;Vs为无穷大系统电压;θ为有功角;χd∑为电抗。
1.3 建模结果对比
输出R2和RMSE:{'ctaea_r2': 3.324234, 'moead_r2':3.690177}
{'ctaea_recall': 0.890232, 'moead_recall': 0.884517}
将发电机组实际运行数据带入模型预测产生数据后和实际电网运行数据进行对比,产生结果如图2 所示,整体输出结果误差较小,建模能够较好跟随实际情况。
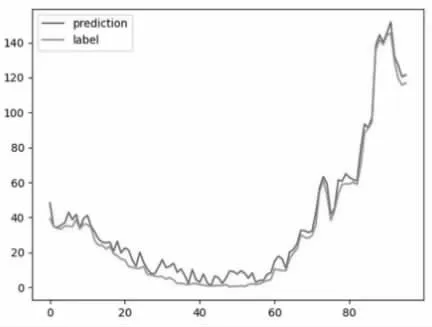
图2 预测值和真实值对比
2 多目标优化算法
2.1 算法约束条件
通过采集电厂实际数据,将建模特征划分为机组特征。这些特征被用作约束条件,将这些约束条件与基于数据驱动的优化算法相结合,通过算法的应用,实现对现实模型的还原和仿真跟随。这个过程旨在实现多个指标的最优化,以满足电厂的多目标需求。
针对调节速度、调节精度、调节时间等开展多目标优化。约束条件包括在进行AGC信号调节时,根据华北地区电网运行准则,通常通过衡量K1、K2、K3来判断性能优劣[10]。
式中,vi,j为机组i 第j 次的调节速率;Ki,j1为要考核的调节速度。
式中,ΔPi,j为机组调节的偏差量;Pi,j(t)为机组实际出力;Pi,j为机组出力指令值,为考核的调节精度。
在机组接收系统指令后,需要一段时间跨出调节死区,这个时间叫做调节时间:
式中,ti,j为机组i 第j 次AGC 响应时间;Ki,j3为调节时间,反映了时间响应的程度,若其值小于0.1,则取0.1。
2.2 M-C融合算法
本文提出一种使用MOEA/D 和C-TAEA 算法融合进行多目标优化,我们定义评价目标函数:
也可以描述为:
式中,λi为非负权重向量;zi为目标函数最小值组成的最优解;k 为要优化的三个指标。
这也就意味着需要对于不同的权重向量。MOEA/D算法在一次运行过程中同时优化N个目标函数。当λi和λj很接近时,拥有和λi很接近的权重向量的G(kλi,z)能获得较好效果。
然而,由于电网存在数据波动、现实传感器误差等原因导致我们的实际数据可行区域不稳定,不考虑可行区域内收敛和多样性的平衡会导致出现局部最优解但不是全局最优解的情况。这时我们引入C-TAEA算法进行协作互补:
式中,F(k)为目标空间的一个候选解;Ω 为决策空间。
这样能有效解决多变量多噪声、不同时间跨度、不同采样区间的问题。
3 结果分析
本文的问题是在研究火电机组供电的情况下对火电机组运行过程进行还原,并对考核指标进行优化分析,获得最高的经济效益。与其他的求解器相比,Pyomo库可以有效建立含有微分方程约束的优化问题,可以建模随机规划问题。
针对不同时刻对于系统整体功率的测算,黄线代表传统PID 控制方法,蓝线为本文的控制方法,可以看到在优化之后,本文系统功率计算优于传统控制算法。
图3 为优化的loss,横轴是迭代轮数,纵轴是Trainning loss。

图3 优化结果的loss 曲线
进行功率提升之后对于系统负荷的对比,在系统整体功率提升的同时,在大约20 个时间单位之后,系统的总负荷与实际工况差异减少,迅速稳定。
本文中提到的AGC(自动发电控制)考核的量化指标,已经在Python 中进行编程。通过结合上述优化后的控制逻辑和对象模型,对下面5 个指标进行了测算,并绘制了相应的图表(见表1)。

表1 优化前后指标实际情况
在基本运行情况下,相较于原来的电厂传统PID 调节算法,改进的融合算法能够较好的提升各项指标,并且满足经济效益要求。
4 结论
本文基于火电机组的调峰调频过程,提出了一种基于数据驱动优化的火电机组调峰调频方法,通过电网指标考核标准来进行模型设计和电网功率快速响应。在整合大量火电发电机组实际运行数据的基础上,运用多目标融合优化策略,对比实际运行工况下的运行数据,有较大程度提升的同时,满足最新标准,实现节能低碳目标,为电厂带来实际效益。

