面向确定性传输的新型虚拟卫星编队方案

徐川，周密，赵国锋，崔钊婧，何熊文

（1.重庆邮电大学通信与信息工程学院，重庆 400065；2.复杂环境通信重庆市重点实验室，重庆 400065；3.中国空间技术研究院北京空间飞行器总体设计部，北京 100094)

0 引言

随着航空航天、移动通信等技术的快速发展，空间信息网络已经成为未来网络发展的重要方向[1-2]。基于卫星的快速位置报告、遥感遥测、应急搜救等时敏业务需求快速增长，业务对端到端数据传输的确定性（丢包率和时延抖动）提出了更高的要求[3]。如图1 所示，a、b、c表示卫星与主星的距离，f1、f2、f3表示不同业务。近年来，由于卫星编队飞行队形控制严格，网络结构相对稳定，被用来支撑时敏业务的确定性传输[4]。但卫星编队飞行的稳定队形依赖于编队中卫星之间的协同控制性能和实时交互能力[5-6]，而频繁的指令交互、姿态控制导致星上额外的计算开销。同时，当任务需求变化时，卫星编队飞行需要进行重新规划轨道、调整卫星形态、重新分配任务等过程，单个卫星编队飞行很难服务于不同业务的端到端传输需求[7]，如要部署多个时敏业务，卫星编队飞行灵活性差，且成本巨大。

图1 卫星编队飞行示意

然而，当前大规模LEO 星座覆盖广、组网灵活，发展迅速，Starlink、OneWeb、Telesat 等新兴星座已成为空间信息网络的重要代表，为偏远地区、时敏通信等提供了条件，且LEO 网络正朝着大规模、多层轨道面部署的方向蓬勃发展[8-9]，不同轨道面卫星之间形成的跨层链路提升了链路的多样性，也能减少传输跳数以优化时延。其中Starlink 为每颗卫星配备了星间链路，连接星座内同轨或异轨卫星，建立高容量、低时延的LEO 网络[10]。如图2 所示，考虑两层LEO卫星星座HLEO（high LEO）和VLEO（very LEO）场景，当执行某项时敏任务时，如能根据卫星星座拓扑，从规定区域中选取同层或不同层中运动相对稳定的多颗卫星，组成一个临时卫星编队（如图2 中快速位置报告编队），任务结束后自动释放卫星资源，使之构成一个灵活而稳定的卫星编队网络，替代传统的卫星编队飞行支撑时敏任务的确定性传输，这将大幅减少卫星编队飞行的编队控制成本；同时，通过在卫星上引入网络功能虚拟化技术，可以在相同卫星节点上构建出多个虚拟卫星编队，满足不同任务的同时部署与资源的灵活调度。

图2 虚拟卫星编队飞行示意

然而，LEO 节点动态性强，星间存在相对运动，如何在LEO 网络中选择多颗稳定的卫星节点是构建虚拟卫星编队亟待解决的问题。

本文面向时敏业务的确定性传输需求，提出了虚拟卫星编队的构想，并给出了卫星编队选择算法，主要贡献如下。

1) 面向时敏任务的不同传输指标需求，提出了基于LEO 网络的虚拟卫星编队思路，给出了相关概念，并深入分析了虚拟卫星编队设计的技术优势和建立虚拟卫星编队所面临的挑战。

2) 针对虚拟卫星编队动态选择问题，构建卫星运动模型以刻画卫星的相对运动对星间链路时延变化的影响，对链路的剩余生存时间、时延变化边界进行分析，以时敏业务的端到端时延需求为目标，提出基于蚁群优化理论的虚拟卫星编队选择算法。

3) 基于STK（systems tool kit）和Exata 搭建实验场景对比分析虚拟卫星编队性能，仿真结果表明，相对于卫星编队飞行方案，虚拟卫星编队方案可以达到前者所提供的QoS 性能，且能灵活地满足多种业务的确定性传输要求。

1 虚拟卫星编队分析

具有稳定队形的传统卫星编队飞行能够支撑时敏业务的确定性传输，但会产生额外的计算开销，且不能同时服务多个业务。为此，基于广泛部署的LEO 星座，选取相对稳定的多颗卫星，组成一个临时的编队替代传统卫星编队飞行支撑时敏任务的确定性传输，能大幅降低编队控制成本，提高网络的灵活性。本节将详细分析虚拟卫星编队的特点与优势及构建虚拟编队的技术挑战。

1.1 特点与优势

相对于传统卫星编队飞行，虚拟卫星编队具有独一无二的优势特点，可以灵活地支撑多种业务的确定性传输，提高网络性能。

1) 队形控制

传统卫星编队飞行要求卫星按照一定规律协同动作，保持相对稳定的距离绕飞，为实现空间任务的采集、处理和分析，彼此之间保持紧密连接，卫星需要频繁地进行指令交互和姿态控制，以维持编队的稳定队形。

虚拟卫星编队在已有的可覆盖全球的卫星星座（如Starlink、OneWeb、Telesat 等）中选取部分相对稳定的卫星组成编队，编队成员按照自己的轨道规律周期运行，不再需要对卫星间的相对位置和运动进行控制。

2) 编队灵活性

传统卫星编队飞行往往为单一任务而设计，如侦查、重力场测量、遥感遥测等，难以应对不同的任务需求。当面临任务需求变化时，卫星编队飞行需要进行重新规划轨道、调整卫星形态、重新分配任务等过程，操作复杂且耗时；针对任务需求差异大的不同任务，需要设计多个不同的卫星编队飞行，灵活性差。

虚拟卫星编队面对不同业务可选取卫星网络中不同区域的卫星来达到目的，不需要重新规划轨道或调整卫星姿态，也不需要多个卫星编队来支撑不同的业务传输，且某一虚拟卫星编队中的成员卫星也可作为其他业务编队的成员，灵活性强。

3) 资源利用率

星上资源有限，传统卫星编队飞行频繁的指令交互和姿态控制，需要耗费额外的资源。相反，虚拟卫星编队不需要耗费额外的资源去进行队形控制，资源开销小；此外，在星上部署网络虚拟化技术，一个物理卫星节点可以作为不同虚拟卫星编队的节点使用，系统整体资源利用率高。

4) 卫星间相对运动

LEO 具有高移动性，导致网络呈现时变特性。相对于传统的卫星编队飞行，虚拟卫星编队无严格的队形控制，成员卫星节点间会有相对运动，这要求在业务传输中考虑卫星的相对运动，确保业务的确定性传输。

总体来说，传统卫星编队和虚拟卫星编队的特征对比如表1 所示。

表1 传统卫星编队和虚拟卫星编队的特征对比

1.2 构建虚拟卫星编队的技术挑战

如前文所述，在LEO 网络中构建虚拟卫星编队飞行给时敏业务的多跳传输带来了巨大的优势。但同时，面对灵活的任务需求，卫星节点动态性强，星间存在相对运动，如何在动态拓扑下选择出较稳定的虚拟卫星编队飞行面临着如下技术挑战。

1) 链路通断导致业务丢包问题

基于LEO 网络的业务往往通过多跳链路进行数据传输，由于星间链路会随卫星运动而发生通信中断，引起数据传输中的延迟、中断及路径切换等，导致业务数据丢包，降低网络性能。

2) 链路距离变化导致时延不稳定问题

星间链路距离的变化（变短或是变长），引起链路传播时延变化，而时敏业务的传输往往需要经过多跳星间链路，任意一跳链路的传播时延变化都会带来端到端时延抖动问题。

为了达到编队飞行的性能要求，在进行虚拟卫星编队构建时，需要通过以下指标来衡量编队选择的性能。

1) 时延有界

时敏业务的确定性传输需要保证数据包的时延在一定范围内，虚拟卫星编队飞行需要满足时延的性能要求。

2) 丢包率

丢包会导致数据传输的不完整性和不可靠性，影响数据的准确性和实时性。卫星节点间链路切换会导致传输中出现丢包。因此，在选择虚拟卫星编队节点时，需要考虑丢包率性能指标。

3) 抖动

抖动是指端到端时延的变化量。过高的抖动会导致数据传输的不稳定性。虚拟卫星编队成员节点间的相对运动会引起星间链路（尤其是层间链路）的距离变化，从而增加端到端时延抖动。

2 虚拟卫星编队建模

面向业务持续一段时间内的确定性传输需求，星间相对运动情况会直接影响虚拟卫星编队的节点选择，本节将详细分析LEO 网络模型以及虚拟卫星编队选择模型。

2.1 LEO 网络模型

如图3 所示，面向基于卫星的确定性业务需求，本文考虑两层LEO 星座VLEO（very LEO）和HLEO（high LEO）场景，可实现全球覆盖。LEO 星座拓扑描述为G=(V,E)，V=VH∪VL，E=EH∪EL∪EH-L，其中，VH、VL、EH、EL、EH-L分别表示HLEO、VLEO 的卫星集合、HLEO 的ISL集合、VLEO 的ISL 集合以及HLEO-VLEO 的层间ISL 集合。其中，同层轨间、不同层间链路会随卫星的相对运动而发生变化。

图3 LEO 网络场景

1) 时敏业务模型

时敏业务f定义为一个七元组f:〈sf,df,sif,,tf,dlf,jtf〉，其中，sf和df表示业务f的源端和目的端；sif表示业务f的数据量大小；表示业务f开始传输时刻；tf表示业务f的持续时间；dlf表示业务的时延要求；jtf表示业务f的端到端抖动要求。

2) 星间链路建模

目前，LEO 间的链路多为激光链路[11]，卫星必须能看到其他卫星才具备通信条件，所以需要对卫星进行可见性分析；其次，卫星间如果存在较大的相对运动，卫星上的天线需要实时调整指向，在这种情况下，由于星上机械天线调整，可能会对星体的稳定性造成影响，因此还需对相对角速度进行分析。因此，对卫星进行可见性分析以及相对角速度分析是为时敏业务选择合适的虚拟卫星编队的前提条件。

如图4 所示，R为地球半径，RL、RH分别表示VLEO、HLEO 轨道半径，ME表示地球的质量，Si表示卫星，Gi表示地面节点，α为地面节点对卫星的最小仰角。在卫星运行过程中，根据卫星轨道参数可以确定卫星任意时刻在地心坐标系中的位置。因此，各卫星以及地面节点的位置矢量为r=(x,y,z)，速度矢量为v=(vx,vy,vz)。由以上参数可得如下关系。

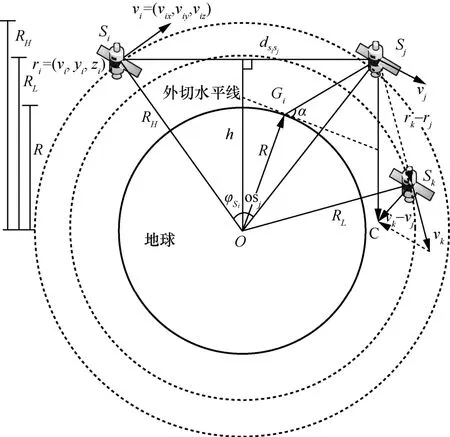
图4 卫星轨道参数

卫星Si的轨道Li周期TLi

其中，G为引力常量。

两颗卫星Si、Sj的星间距离dij为

两颗卫星Si、Sj的相对位置矢量rij为

两颗卫星Si、Sj的相对运动速度vij为

任意两矢量ri、rj之间形成的夹角φ为

其中，·表示点乘。

地心O到两颗卫星Si、Sj连线的距离h为

由于星间链路通过大气层会导致信号衰减，在地球表面设有最小保护余隙H。因此，卫星间可见需满足

其中，h可由式(6)计算。

相对角速度。由式(4)可得单位时间内相对位移矢量v0=vjk，则Sj指向C 点的矢量为rk-rj+v0，于是可以得到单位时间内卫星Sj的转角γ

假设星上机械天线的最大角速度为ωm，因此，在可见基础上，若两颗卫星的相对角速度大小使式(10)成立，则认为星间链路建立成功。

2.2 虚拟卫星编队选择模型

1) 剩余生存时间

卫星网络中星间链路的生存时间不同，导致业务的传输路径生存时间不同，所以在业务要求持续时间内，业务通过不同路径进行数据传输，传输路径的切换次数会有差异，进而引起数据丢包不同，因此需要考虑传输路径的生存时间。

链路生存时间。卫星间的相对运动易导致轨间、层间的星间链路发生中断，链路从连接到断开的一段时间称之为链路生存时间。

图5 链路生存时间分析

假设在一定时间内，没有其他因素干扰，两卫星节点保持相对速度方向不变，卫星Si相对静止，卫星Sj以相对运动速度做匀速直线运动。当卫星Sj到达D点时，两点间相对距离达到可通信的最大距离，继续运动星间链路将断开。本文定义该时间为链路lij生存时间，结合图5 中的辅助线，化简可得

业务f传输路径的剩余生存时间。卫星源端到目的端的第j条可达的传输路径记为Pj，则t时刻Pj的剩余生存时间为该条路径上所有星间链路的剩余生存时间中最小的一个，即

2) 距离变化率

卫星网络中任意一跳链路距离变化都会引起传播时延变化，进一步导致端到端时延抖动，因此需要考虑传输路径的链路距离变化情况。

星间链路距离变化率。卫星间的相对运动易导致轨间、层间的星间链路距离发生变化，本文将星间链路剩余生存时间(t)内的变化情况定义为星间链路距离变化率(t)，具体可表示为

传输路径的距离变化率。在t时刻路径Pj的路径距离变化率(t)为该条路径上所有星间链路的距离变化率最大的一个，即

3) 面向确定性业务需求的传输约束

端到端时延约束。业务持续时间内，其端到端时延必须要在时延要求范围内，表示为

传播时延。传播时延是指激光在星间无线信道中传播一定距离所花费的时间，由传播距离d和传播速度vc决定。然而，在卫星网络中，星间链路的距离dij随着卫星运动而发生变化。因此，[t,t+Δt]星间链路lij的传播时延的计算式为

传输时延。传输时延是指卫星节点发送每个数据包所需要的时间。传输时延取决于数据包大小B（单位为bit）和发送速率R（单位为bit/s），卫星节点si的传输时延计算式为

处理时延。处理时延是指卫星节点在收到数据包时通过软件和硬件对其进行处理所花费的时间。处理时延由缓存大小BS（单位为bit）与设备处理速率SP（单位为bit/s）的比率所决定，卫星节点si的处理时延计算式为

排队时延。排队时延是指数据包在输出缓存区中传输到链路之前排队（等待）所花费的时间。排队时延的大小取决于等待传输的数据包数量（队列长度），并且受卫星节点具体的资源调度策略和数据包到达方式等因素的影响。节点Si的排队时延记为。因此，t时刻业务传输路径的总时延可以描述为

端到端时延抖动约束。业务的端到端时延抖动需在抖动要求范围内，表示为

信噪比（SNR）约束。由香农定理可知，卫星节点间ISL 的信噪比[12]决定着星间链路能够进行数据无差错可靠传输的最大信息速率。在星间进行数据传输时，若SNR 小于预设阈值，数据传输很可能发生中断，无法保障ISL 的通信质量。t时刻路径Pj的信噪比SN(t)约束表达式为

节点缓存约束。为保障接收节点能够成功接收数据，接收节点需要有缓存队列长度以接收或处理数据。假设网络中节点具有相同的最大缓存队列长度为β，在t内接收节点等待处理的数据量Xn，新到达业务数量为A(t)，可处理业务数量为D(t)，那么t时刻该节点的数据队列长度可以表示为X(t)=Xn+A(t)-D(t)。t时刻路径Pj的节点缓存资源约束(t)表达式为

其中，XPj(t)定义为路径Pj的剩余生存时间TPj(t)内的链路中的缓存资源最大值。

3 面向时敏业务的虚拟卫星编队选择算法

由虚拟卫星编队选择模型可见，虚拟卫星编队选择时需要满足时敏业务的服务时长和QoS 指标要求，本节以时敏业务的确定性传输需求为目标，选择最稳定的虚拟卫星编队为其服务。

3.1 优化目标

为满足业务需求时间内的确定性传输，所选择的编队需尽可能为业务提供持续稳定的传输路径。基于虚拟卫星编队选择模型可知，传输路径的生存时间取决于其所包含链路中最短生存时间的链路，当一条传输路径不足以满足业务的持续时间要求时，需要为业务规划多条传输路径，但路径切换过程中易发生数据丢包，选择生存时间较长的传输路径，业务切换过程中的丢包较少；其次，卫星节点之间的链路距离变化将引起的星间时延抖动，路径距离变化小的传输路径更优。

因此，本文以剩余生存时间和距离变化率来量化传输路径的稳定性，以最大的路径剩余生存时间和最小距离变化率为目标，为业务选择稳定的传输路径，目标函数如下

其中，约束C1表示路径Pj的端到端时延要在业务的截止时间dlf内；C2表示路径的端到端时延抖动要在业务要求jtf内；C3表示路径的SNR 要大于预设阈值α，否则数据传输很可能发生中断；C4表示路径的队列长度要小于预设阈值β，否则节点很可能无法接收或处理数据。

3.2 虚拟卫星编队选择算法

根据3.1 节的分析，本文把卫星网络中的编队选择问题抽象成为时敏业务选择最优路径的问题模型。由于该模型通常是一个NP 难问题，而蚁群优化（ACO,ant colony optimization）算法已经成功地应用于解决LEO 网络中的路径选择问题[14]。因此，本文基于改进ACO 算法求解目标函数，求出业务持续一段时间内的最优路径集合，路径上的卫星节点集合作为虚拟卫星编队的成员集合。针对一段时间的确定性业务需求，本文设计了基于ACO的虚拟卫星编队选择算法，如算法1 所示。

算法1基于ACO 的虚拟卫星编队选择算法

为了使算法能够更好地适应不同规模的卫星网络，算法1 中的初始化信息素浓度τij()在大规模卫星网络中采用均匀分布减少计算，在小规模卫星网络中采用不均匀信息素分布，更有针对性地搜索解空间，进一步提高效率，且需调小δ0，使其更多地探索新路径。

4 实验仿真与结果分析

4.1 场景设置

为验证本文所提出的虚拟卫星编队构建算法的可行性与有效性，使用STK 搭建一个两层LEO网络场景，轨道高度和倾角相关参数参考Starlink星座的Phase 1 的Shell 1、Shell 2 进行设置[16]，如表2 所示。并基于Exata 进行虚拟卫星编队方案与传统卫星编队飞行[4]的实验对比。

表2 卫星网络场景参数

根据文献[13]对仿真实验参数进行设置，如表3所示。

表3 仿真参数

此外，为了验证本文所提虚拟卫星编队方案对多种时敏业务传输的支撑效果，根据文献[17-18]设置多种时敏业务，根据文献[19-20]设置其QoS 指标要求，同时也设置一种大范围监视业务，业务参数如表4 所示。

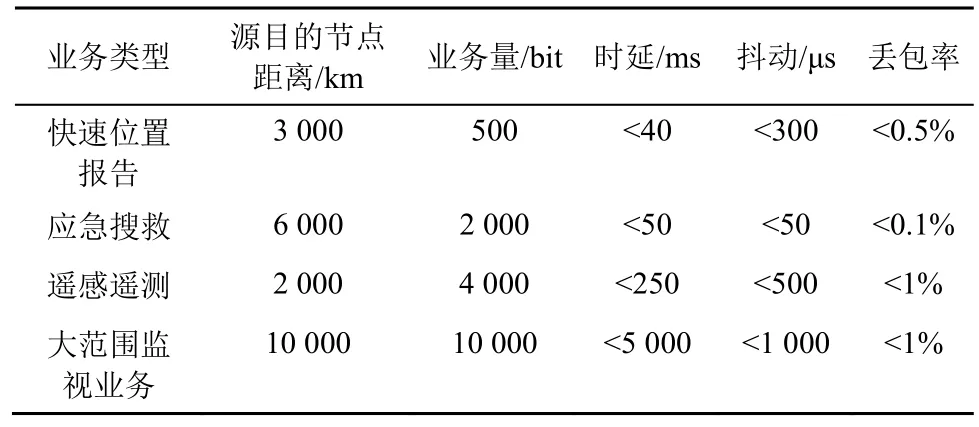
表4 业务参数

STK 三维仿真场景及业务设置示意如图6 所示。

图6 STK 三维仿真场景及业务设置示意

4.2 与传统卫星编队飞行对比分析

本节对比传统卫星编队飞行与虚拟卫星编队对同一时敏业务的服务质量，针对同一时敏业务（如快速位置报告）的确定性要求，选择同一对源节点和目的节点加载时敏业务，源节点和目的节点之间距离3 000 km，数据量大小为500 bit，时敏业务的开始传输时刻由15 s 到300 s 以步长15 s 不断增加，测试其在300 s 内的编队服务性能（单颗卫星对地覆盖的时间一般为300～600 s，传统卫星编队飞行为业务提供至少300 s 的服务），对比虚拟卫星编队与传统卫星编队飞行的业务传输性能指标。

如图7(a)所示，当源节点和目的节点同半球时，传统卫星编队为业务提供的端到端时延范围为[16.72,16.81]ms，虚拟卫星编队提供的时延范围为[16.63,16.82]ms，时延范围扩大了0.1 ms，在180 s时由于虚拟卫星编队（东北方向运行）中的业务传输路径发生切换，时延出现波动。如图7(b)所示，当源节点和目的节点跨半球时，传统卫星编队为业务提供的端到端时延范围为[22.15,22.21]ms，虚拟卫星编队提供的时延范围为[21.98,22.28]ms，时延范围扩大了0.24 ms。由于传统卫星编队飞行会实时控制队形，在同半球和跨半球的时延均较稳定，而虚拟卫星编队的星间距离会随时间变化，对端到端时延有一定影响，但均能满足时敏业务的时延传输要求。

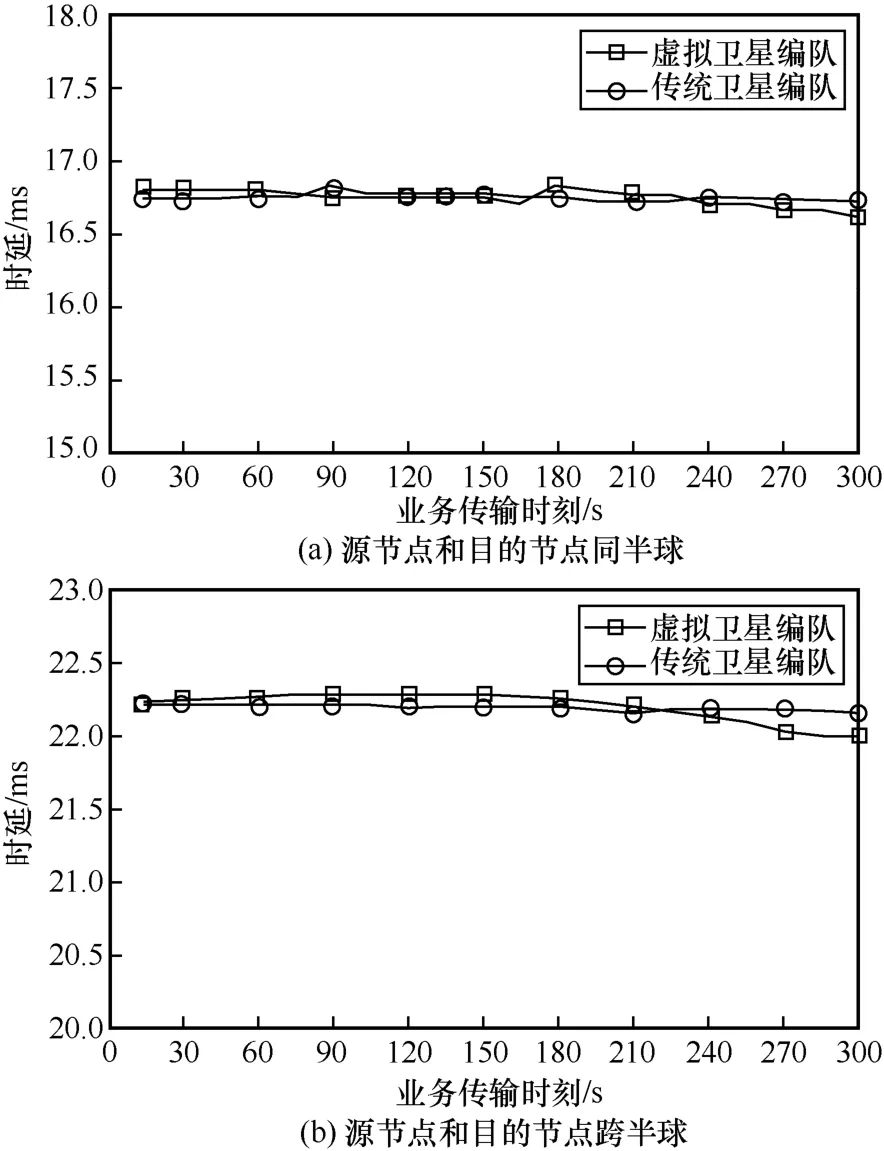
图7 不同传输时刻下的时敏业务端到端时延

如图8(a)所示，当源节点和目的节点同半球体时，传统卫星编队为业务提供的端到端时延抖动范围为[3.0,7.4]μs，虚拟卫星编队提供的时延抖动范围为[0.8,9.6]μs，抖动范围扩大了4.4 μs，在180 s时由于虚拟卫星编队中的业务传输路径发生切换，抖动会出现较大的变化。如图8(b)所示，当源节点和目的节点跨半球时，传统卫星编队为业务提供的端到端时延抖动范围为[3.0,7.6]μs，虚拟卫星编队提供的抖动范围[0.1,9.7]μs，抖动范围扩大了5.0 μs。总体来说，传统卫星编队飞行在同半球和跨半球的端到端时延抖动在一定范围内波动，受编队的控制精度影响；虚拟卫星编队飞行中，抖动受到传输路径的轨间链路距离变化率的影响，但均能满足时敏业务的抖动传输要求。

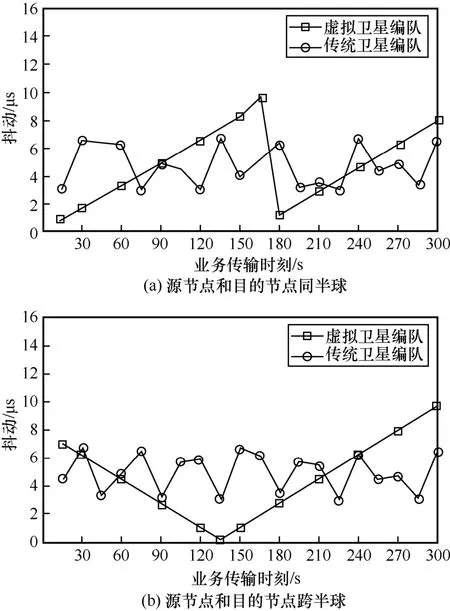
图8 不同传输时刻下的时敏业务端到端时延抖动

如图9(a)所示，当源节点和目的节点同半球时，传统卫星编队为业务提供的丢包率范围为[0.03%,0.043%]，虚拟卫星编队提供的丢包率范围为[0.03%,0.08%]，在180 s 时由于虚拟卫星编队中的业务传输路径发生切换，丢包率会增加。如图9(b)所示，当源节点和目的节点跨半球时，传统卫星编队为业务提供的丢包率范围为[0.032%,0.044%]，该虚拟卫星编队提供的丢包率范围[0.032%,0.043%]，其始终存在一条路径满足要求，丢包率无明显变化。总体来说，随时间变化，丢包率保持相对稳定，均能满足时敏业务的丢包率要求。

4.3 虚拟卫星编队支持多业务灵活部署

本节验证所提虚拟卫星编队方案能够支撑多种时敏业务的传输，设置如表4 所示的业务，共4 种类型，测试其传输不同类型业务的编队性能；此外，随机选取多组源节点和目的节点分别处于地球上不同位置，测试其某一个类型业务（快速位置报告），在多种类型业务（每种类型5 个业务，共20 个业务）同时传输下的编队性能情况。

如图10 所示，面向4 种时敏业务，传统编队飞行构建了4 个不同的编队为其服务，共占用21 颗卫星，且在业务传输中编队卫星不会改变；针对同样的时敏业务，本文方法选取了16 颗卫星构建了4 个虚拟卫星编队，其中有5 颗卫星复用在不同编队中，卫星数量减少了20%以上，当业务动态变化时，也可根据需求实现编队的灵活调整。

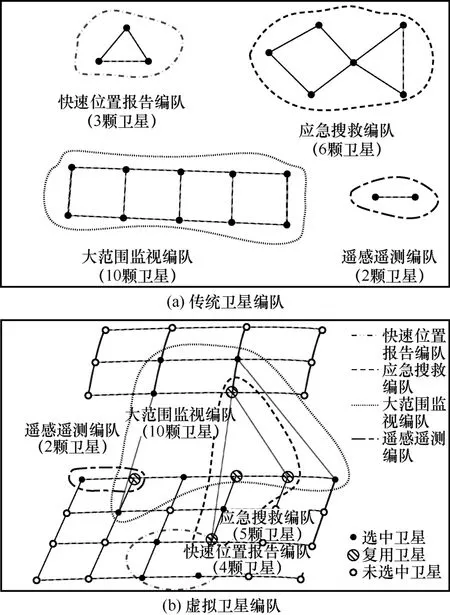
图10 4 种编队部署情况

如图11(a)所示，4 种不同类型业务的端到端时延并没有随时间出现较大的波动，这是因为选择虚拟卫星编队时，考虑了生存时间和距离变化率，使编队相对稳定；另外，在同一条件下，快速位置报告业务的端到端时延最小，大范围监视业务的端到端时延最大，且时延变化相对更大，这是因为快速位置报告业务单位时间内传输的数据量最少，而大范围监视业务的数据量最多，且源节点和目的节点距离最远，星间距离变化带来的影响更大。如图11(b)所示，随着业务数量增多，所需卫星颗数呈现增长趋势，但增长速度逐渐变缓，这是因为虚拟卫星编队在已有的LEO 网络中选择稳定的多颗卫星，某一编队中的成员卫星在资源充足的条件下可作为其他编队的成员，提高卫星的资源利用率。

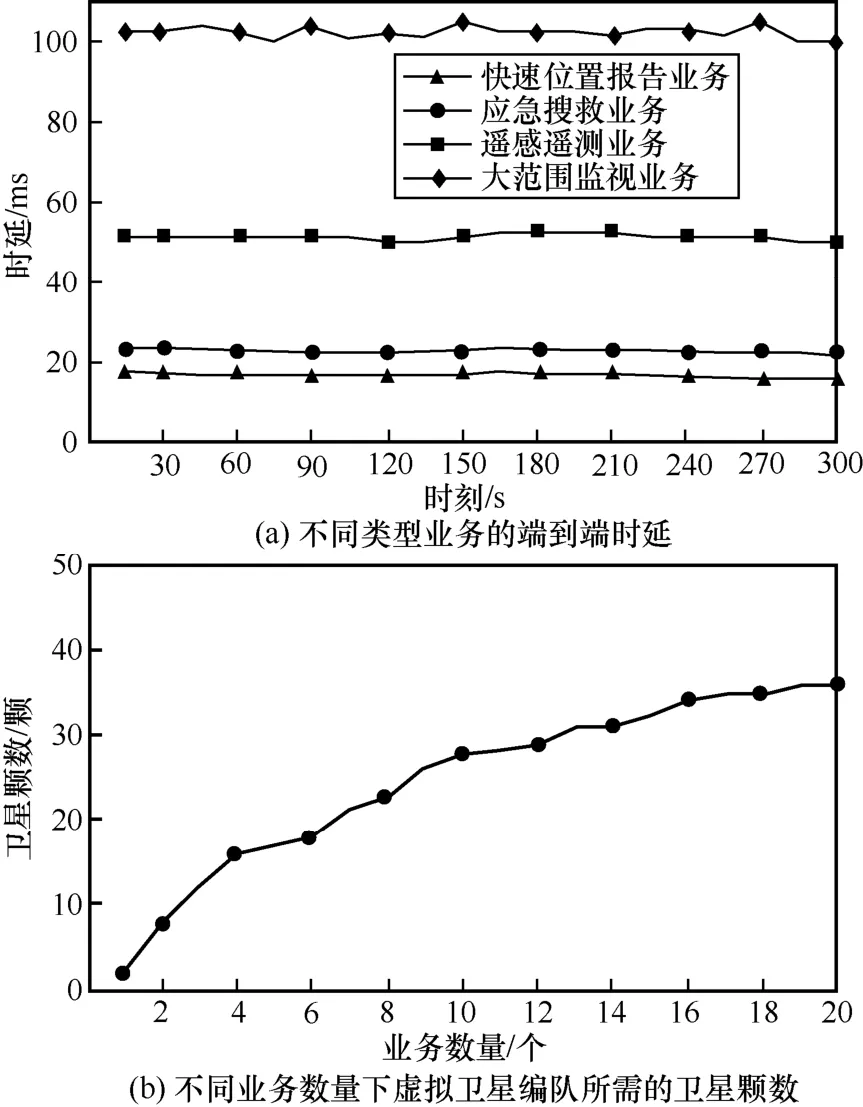
图11 传输多种类型业务的编队性能

如图12 所示，随着其他时敏业务数量的增加，当前的快速位置报告业务的时延、抖动、丢包率整体上呈增长趋势，这是因为随着其他业务的加入，该快速位置报告编队的成员卫星节点会与其他业务的编队共用卫星节点资源，从而会影响当前业务的传输性能，但其在不同数量的业务传输的影响下，时延、抖动、丢包率仍然能够满足该时敏业务的需求，并且能够同时支撑多业务的灵活部署。

图12 快速位置报告虚拟卫星编队在多个业务传输下的编队性能

5 结束语

面向确定性传输业务需求，针对传统卫星编队飞行需要实时队形控制导致额外资源开销，并且面临多个业务时不够灵活的问题，本文提出了虚拟卫星编队构想来支撑确定性传输。首先分析了基于低轨星座的虚拟卫星编队的设计挑战和性能指标；然后，通过刻画星间链路的生存时间与距离变化率等属性，建立了虚拟卫星编队节点选择模型；最后，以该模型为基础，基于时敏业务设计虚拟卫星编队飞行选择算法。仿真结果表明，所提虚拟卫星编队方案能够为时敏业务提供确定性传输，还能同时支撑多种业务同时传输。