基于VMD-SampEn-M1DCNN 组合模型的钳形电流互感器故障诊断

孙晓峰，崔 晋，刘春晖，宫振宇，朱 博，姬少培

（1.国网赤峰供电公司，内蒙古 赤峰 024000；2.中国电子科技集团公司第三十研究所，四川 成都 610041）

0 引 言

现阶段，电力系统中的电流互感器在进行常规运作时，需要面对高温、电磁干扰等因素的影响，再加上长时间工作的需要，互感器电子器件特性将大受影响，进而演变成为不同类型的故障问题[1-2]。在上述故障因素的影响下，互感器精度持续下滑，难以及时记录电气量信息；此外，互感器可靠性的降低会对电力系统安全性、经济性等产生直接影响[3]。所以需要研发高效的、高质量的电流互感器故障诊断方法，有效控制电网建设成本，保持安全运行的稳定性。

基于电流互感器出现突变式、渐变式故障风险，现阶段主要的故障诊断方法包括基于知识、基于解析模型、基于信号[4-6]三种。王洪彬等结合互感器的渐变性故障问题，首次提出关于互感器的模拟观测模型，提前设定限制条件，及时获取故障资料[7]。丁涛等人对比分析双端交换电流信息、互感器输出电流信息，完成在线故障信息的检验[2]。王涛等人将互感器故障划分为3 个类型，基于小波降噪和小波分解方法进行样本数据分析，随后对诊断结果进行检验[8]。王昕等认为互感器故障诊断方法是主元分析法的基础，利用样本信号判断获取故障信息，并针对故障具体情况进行检验[9-10]。虽然该类型故障诊断方法已经取得良好的效果，但是高度依赖传统信号分析技术，这需要计算机的计算和工程师经验的配合，不利于模型诊断效率的提升[11]。

结合上文所述的内容，电流互感器故障诊断效果与模型性能、经验知识、系统异常干扰信号等方面有直接关系。通过对上述问题分析，本文重点研究各类型影响钳形电流互感器稳定性的因素，客观分析故障模式类型，以此得到数据模型；并提出了一种基于VMDSampEn-M1DCNN 组合模型的钳形电流互感器故障诊断模型。该模型在结合VMD 与SampEn 优势的同时，构建了多个不同的一维卷积神经网络的集成网络模型，直接将VMD、SampEn、M1DCNN 三者进行融合，以此满足互感器故障诊断需求。

1 相关理论基础

1.1 变分模态分解

变分模态分解属于新的信号分解变分方法，主要目标是进行输入信号的创建，并且将实值输入信号f分解成固定稀疏特性子信号[12]。VMD 在实现过程中，需要以式（1）为基础，对问题进行构造和拆解：

在操作时，二次惩罚项α、拉格朗日乘子λ作用在变分问题时不会受到约束和影响。二次惩罚项α能确保信号在高斯噪声环境中进行精度重造，拉格朗日乘子λ则可以保障约束的有序执行，增广拉格朗日函数参考如下公式：

公式（2）鞍点属于公式（1）对应的解，能通过交替方向乘子法（ADMM）进行计算。预先设定分解模态数中，可通过初始化模态建立频域表达式、中心频率以及拉格朗日乘数λ1；然后根据以下公式分别进行模态和中心频率的更新：

通过单次更新后，即可获取新模态和中心频率，在拉格朗日乘数中，可结合公式（5）更新：

持续迭代确保完成收敛处理，计算公式如下所示：

从上文的描述可以看出，在VMD 中有4 个参数需要提前指定，分别为模态数K、模态分量频率带宽控制参数（或二次惩罚项）α、噪声容限τ和收敛准则容忍度ε。与前两个参数相比，τ和ε对分解结果的影响很小，因此通常采用原始VMD 算法中的默认值；参数模态数K则一般是在未对待分解信号进行分析的基础上指定的，难以保证模态数的合适性以及信号分解的准确性和效率；参数α则与噪声干扰的抑制性能有关，更应慎重选择。因此寻找与待分解信号相匹配的最优参数组合是VMD 方法的关键。

1.2 样本熵

2000 年，Richman 和Moornan 提出样本熵SampEn 的概念，以此检验时间序列复杂性[13]，计算流程如下：

1）构造一个关于时间序列v(t)的m维向量；

2）按照公式（7）计算m维向量v(i)和v(j)之间的距离：

3）给定一个阈值r，按照公式（8）计算当d[v(i),v(j)]小于r时其与N-m-1 的比值(r)：

式中i= 1,2,…,N-m+ 1，i≠j。

4）按照公式（9）计算Bmi(r)的平均值：

5）重复步骤1）～步骤4），得到Bm+1(r)；

6）按照公式（10）计算时间序列v(t)的样本熵。

当N是一个有限值时，SampEn 可以表示为：

1.3 一维卷积神经网络

这些年来，图像识别和目标检测应用较为普及，这类方法能有效应对、处理过度适应相关的问题，同时能进行更全面的深入学习。CNN 从结构看包括卷积层、全连接层、输出层等[14]。在CNN 结构中，输入层的关键作用是提取图像数据，卷积层内可优先选择卷积核进行操作，能在合理范围内提取数据信息；池化层则用于卷积层的特征提取，但是需要提前完成池处理，进而减少计算量方面的需要。卷积层和池化层需要提前完成交易分布，以此掌握图像的特征信息，使高级别特征较为稳定。全连接层接收网络传输特征后，需要客观分析网络输出情况，在输出层中完成图形的分类处理。卷积层能为CNN 提供功能基础，反观卷积层内部，可以优先考虑卷积核和输入图像，以此参与卷积工作，完成偏置添加后，可通过激活函数分析特征映射。池化层一般情况下都保留在卷积层后端，能适当控制图像的大小。由于其在图像特定区域中，通过相邻像素合并后即可创建独立的代表值，此外，某些意义上能确保特征尺度的固定。CNN 分类阶段正常情况下，通过完全连接层和一个分类器共同组合，可以针对上一层信息完成分类处理[15]。

钳形电流互感器数据属于一维时间序列数据，并且与单个时刻数据点密切相关，若直接将其切换成二维模式，那么将使原始序列空间相关性产生直接影响，并且容易丢失故障信息。1DCNN 则可以有效处理钳形电流互感器数据，1DCNN 输入数据可作为一维信息，随后卷积核本身筛选对应结构，不管是池化层输出还是单个卷积层，其直接匹配一维特征向量[15]，通过图1 可查看1DCNN 信息。

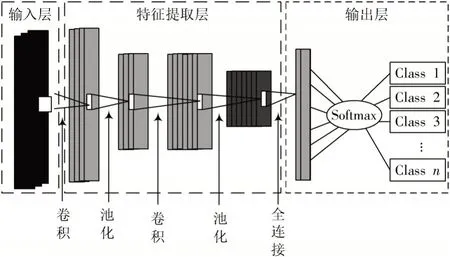
图1 1DCNN 网络结构

1DCNN 在组成结构内，主要包括输出层、特征提取层、输入层。从输入层本身看，能有效融入时间步长数据完成分割处理；但是从提取层本身看，需要考虑其他层的关联性；通过卷积层能完成多卷积核提取，并妥善掌握多种特征向量。池化层则顺利进行特征向量降维处理，保障非线性特征鲁棒性稳定，结合卷积层和池化层的共同作用，能进行数据提取，随后通过连接层组合成为分类层。从分类层整体看，首个全连接层可以实现特征进行平坦化的管理，也表明特征向量将从头向尾建立一维向量。反观在全连接层中，数据样本情况、神经元数量等基本保持协调，针对输出层可应用Softmax 回归分类器，随后完成类别输出管理。

2 M1DCNN 模型

因为单个网络结构相对简单和直接，参数选择难度较高，因此单个深度卷积神经网络在进行大规模样本、多类别样本处理时，泛化能力表现欠佳。为避免个别深度卷积神经网络性能受到影响，适当提升模型的综合水平，集合不同的深度卷积神经网络是较为理想的方案。激活函数要求进行非线性运算，结合多个激活函数神经网络呈现差异化的数据，使互补学习质量大幅提升。

为挖掘多个特征卷积神经网络情况，将常用激活函数均纳入隐藏层函数。表1 中包含3 种类别激活函数公式、导数，主要类型包括指数运算和非指数运算。在数十年的发展中，神经网络使用较多的是Sigmoid 和tanh等指数运算函数，但是在使用过程中依然面临计算代价高、梯度消失等风险[16]。针对非指数函数，近年来使用较为普及的是ReLU，其有着极高的运算速度，能有效减少梯度消失的影响，但反观函数输入时，并非以0 作为核心，整体稳定性严重不足。

表1 3 种激活函数

式中：β为稀疏惩罚因子；ρ j为平均激活值；ρ为稀疏参数；m和p为输入向量维数。

为提升泛化能力和诊断质量，应该积极建立不同类型激活层，但是前提是保持1DCNN 创建的一致性，具体操作中，可选择1DCNN 训练的方式，自低向高完成特征提取，具体方法为：首先，通过前期整理的数据，将其输入至首个卷积层，随后获取特征1，如此类推，获取特征2；再将学习中高层特征置于Softmax 分类器，即可完成故障模式分析。

建立1DCNN 后，需要设计故障诊断组合策略。结合多组合策略分析结果，投票正常情况下都会选择简单和直接的策略，并且整合不同的集成学习方案。多数投票原则下，故障诊断策略主要包括如下几个部分的内容：

1）获取网络输出结果，识别精度信息；

2）为保证单个网络模型输出稳定，应执行多次实验步骤；

3）充分考虑实验结果，随后通过多数投标策略完成数据分析，总结最终的结果。

M1DCNN 模型整体实现流程如图2 所示。

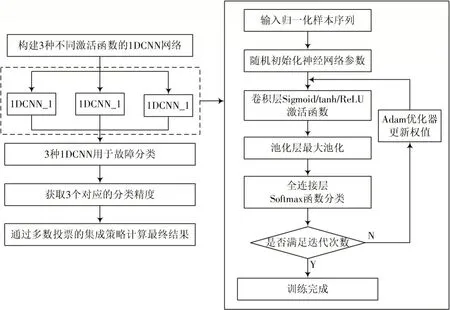
图2 M1DCNN 实现流程

3 基于VMD-SampEn-M1DCNN 组合模型的钳形电流互感器故障诊断

基于VMD-SampEn-M1DCNN 组合模型进行电流互感器故障诊断的整体流程如图3 所示。具体操作流程如下：

1.2 治疗方案 确诊患者按照AL的标准化疗方案进行诱导治疗，其中AML多采用以阿糖胞苷为主的吡柔比星+阿糖胞苷(TA)、米托蒽醌+阿糖胞苷(NA)、伊达比星+阿糖胞苷(HA)等方案，ALL多采用以长春瑞滨+地塞米松(VP)为基础的吡柔比星+长春瑞滨+培门冬酶+地塞米松(DVLP)、吡柔比星+长春瑞滨+培门冬酶+环磷酰胺+地塞米松(DVLCP)等方案。强化巩固治疗多使用原诱导缓解方案及大、中剂量阿糖胞苷单药交替化疗。

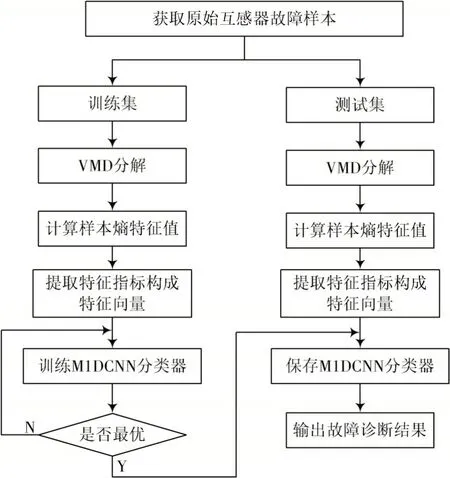
图3 基于VMD-SampEn-M1DCNN 的钳形互感器故障诊断模型实现流程

1）将钳形电流互感器数据分配为训练集和测试集；

2）针对单独样本实施VMN分解，以此获取IMF分量；

3）计算样本熵特征，并组合为特征向量；

4）构建多个一维卷积神经网络模型，基于多数投票的原则建立集成学习策略；

5）在M1DCNN 中，利用训练样本检验特征学习，并完成故障诊断。

4 仿真实验与结果分析

4.1 实验数据集

通过对钳形电流互感器的稳定性进行分析，可获取不同正常模式和不同故障模式下的数学模型，详细情况如表2 所示。针对单独模式下的介绍和参数，可通过参考文献[17]获取。利用钳形电流互感器健康状况的模拟测试，得到不同状况下的样本数据。

表2 电流互感器的故障模式和数学模型

对比分析钳形电流互感器的故障模式并进行模拟，以此分析在正常模式和4 个故障模式下前行电流互感器输出数据的不同，具体见图4。针对单个模式，数据样本总计600 个，具体信息如表3 所示。

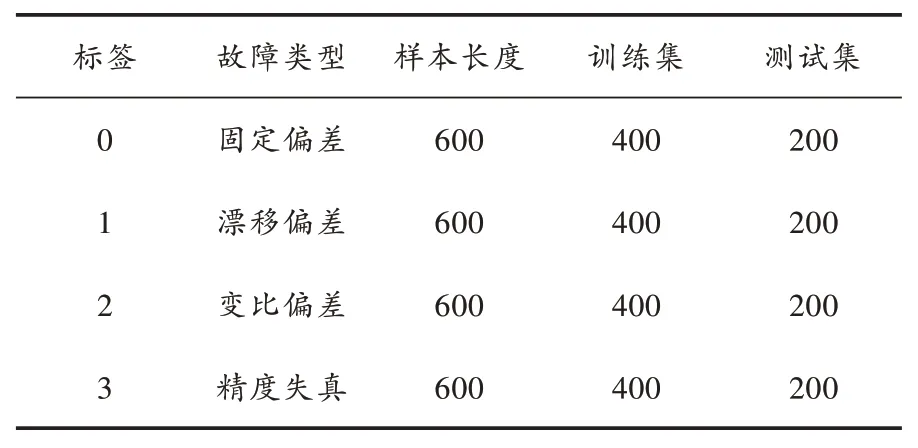
表3 故障数据集描述

图4 互感器各种状态的输出数据

4.2 参数选择

4.2.1 VMD 中IMF 分量选择

本文将结合VMD 分解处理钳形电流互感器数据，在VMD 分解操作下，即可判断IMF 分量、原始信号的相互影响关联。

本文将IMF 分量和电流互感器数据之间的相关系数作为保留哪些IMF 分量和拒绝哪些IMF 分量的评价标准，相关系数最高是1，IMF 分量与原始电流数据相关系数曲线如图5 所示。

图5 不同IMF 分量的相关系数

结合图5 信息可以判断：相关系数将在IMF 提升的同时持续降低，3 个IMF 分量与原始信号保持较强的相关性，并且具备较高的相关系数。结合第4～8 个IMF 分量进行分析，相关系数都在0.4 以内。本文在实验时仅针对3 个IMF 分量。

4.2.2 样本熵参数选择

结合1.2 节中样本熵计算分析可判断：SampEn 值与维数m、阈值r有直接关联，根据文献[20]的研究，SampEn 中的m值通常为1 或2，r的取值通常在0.1～0.25之间。本文选择m=1 和r=0.2 采样数据，并计算具体的SampEn 值。

4.2.3 卷积核数量选择

为保证模型具备快速、高效的故障诊断功能，对网络训练参数完成优化处理，即创建一维卷积神经网络模型；然后，以后一层卷积核数量为基础，坚持比前一层增加100%的原则分析网络卷积核数量。通过图6 可判断卷积核数量、训练时间等的相互影响。结合图6 可知，在各层卷积核数量不断提升时，网络训练时间也在提升，且网络可训练参数也保持指数增长，进而浪费了大量的网络资源。

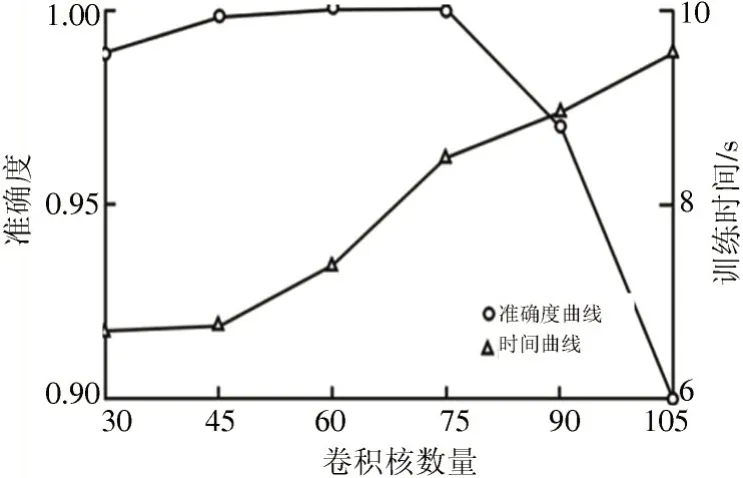
图6 卷积核数量对网络准确度和训练时间的影响

卷积核数量如果控制在60，模型将保留较高的准确性，其所需的训练周期也会缩短，所以综合分析多种因素，卷积核数量控制在60 时网络综合性能最为合理。

4.3 诊断结果与分析

4.3.1 不同激活函数对1DCNN 性能的影响

为客观分析多个激活函数在1DCNN 性能中的影响关系，本文首先利用VMD 和SampEn 进行钳形电流互感器数据的特征提取，并将特征提取结果分别作为1DCNN 和M1DCNN 的输入。在实验室，选择3 种主流的激活函数进行实验分析，随后对比研究实验结果、模型结构等，这样的方式需要持续10 次进行实验，单次实验结果如图7 所示。同时结合10 次实验结果平均水平，将精度、标准差进行汇总，如表4 所示。

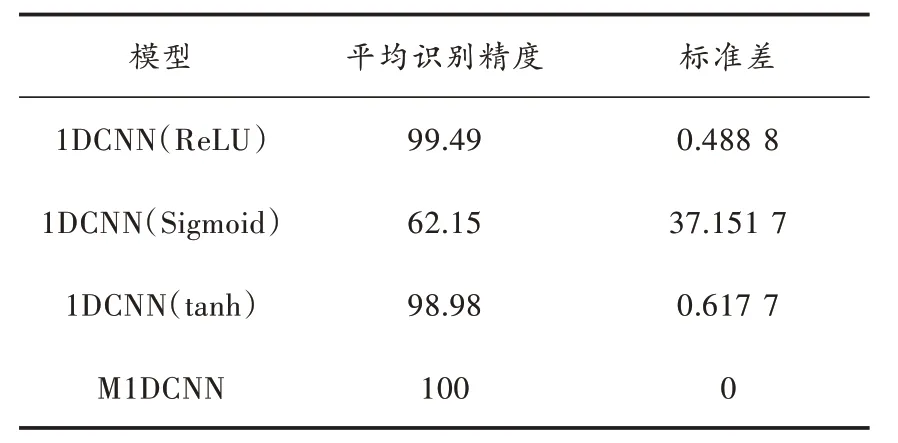
表4 不同模型平均识别精度和标准差%

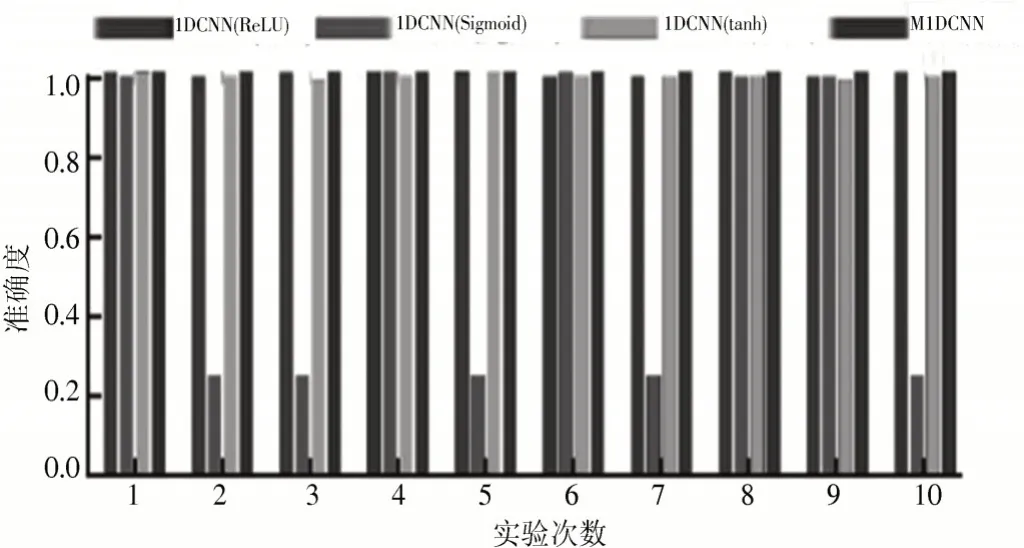
图7 M1DCNN 与不同激活函数的1DCNN 实验结果

从图7 可知，利用M1DCNN 完成故障诊断，能保持较高的识别精准度。反观目前的激活函数类型，ReLU和tanh 对应的1DCNN 结果比模型稍次。参考表4 中ReLU 和tanh 的1DCNN 实验结果，若激活函数为Sigmoid，则1DCNN 标准差相对偏高。从实际的实验次数看，激活函数若为Sigmoid 的1DCNN 实验结果，那么准确度仅为25%。从客观原因看，0 并不代表Sigmoid 激活函数核心，同时伴随着梯度消失的风险，在完善集成策略过程中，可充分考虑其他两种1DCNN 消除梯度，使模型整体性能发挥。图8 所示为在多个激活函数影响下对应的1DCNN 收敛曲线。通过图8 可知，迭代次数持续底层时，3 个模型在迭代5 次后即保持稳定，但是依然需要关注的是，Sigmoid 函数伴随着梯度消失的情况，因此需要把准确度调整在25%，随后保持其稳定性。如果激活函数为ReLU 和tanh 时，双方收敛能力差异并不显著，准确度稳定性将无限靠近100%。

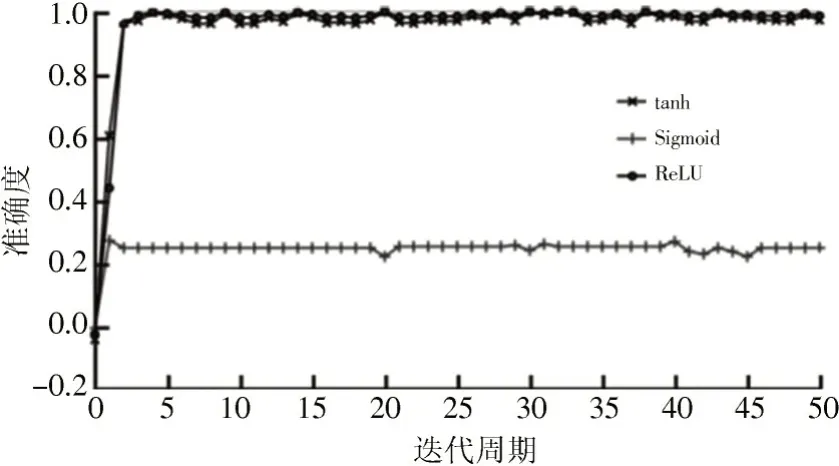
图8 多个激活函数下模型收敛曲线

图9 为不同故障诊断模型的实验结果，对比方法中涉及BPNN[18]、SVM[19]、2DCNN[20]等，不同的方法都需要持续10 次实验，以减少实验的误差，但是所有方法都应该保证其准确度，对应的实验精度确定为100%。通过对比3 种方法，可以从中选择最合适的诊断方案。

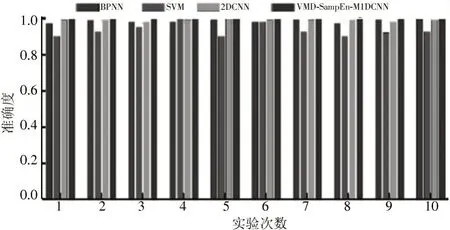
图9 不同故障诊断模型的实验结果

4.3.2 网络可视化

为客观检验VMD-SampEn-M1DCNN 对应的故障误判率，本文通过混淆矩阵的方式检验故障诊断结果、误分类率等信息，具体如图10 所示。通过图a）可知，VMD和SampEn 在提取信息后，将特征信息输入1DCNN，然后创建故障诊断的混淆矩阵；通过图b）能查看特征信息输入M1DCNN 后故障诊断相匹配的混淆矩阵，横轴则用于分析测试集预测标签，纵轴是真实标签。混淆矩阵内部能客观检验角线，以此判断模型分类准确率，针对角线选择误分类率。

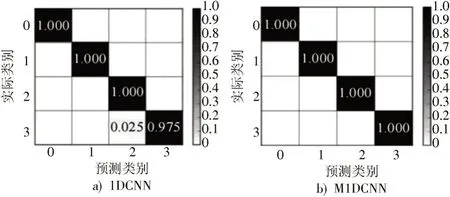
图10 混淆矩阵

通过分析图10 得出，1DCNN 可客观分析故障标签，在精度失真基础上，识别率稳定在97.5%，误判率仅为2.5%，应对其他类型故障时，能进行更精准的判断，且在M1DCNN 故障分析中，识别率保持100%。由此可见，M1DCNN 能保持较好的综合识别精准度，并且在相同类型故障识别中有突出的表现。

一般情况下，直接将CNN 当作独立黑箱，在内部运行机制方面无法被理解。在本文中，通过可视化的方式分析VMD-SampEn-M1DCNN 中M1DCNN 的内部运行机制。

为深刻分析该模型中M1DCNN 的特征提取功能，采用主流的t-SNE 方法，在单层网络测试集数据输出的前提下，完成降维和可视化处理。直接把高维的特征向量映射二维空间，进而创建单层特征分布，具体如图11所示。

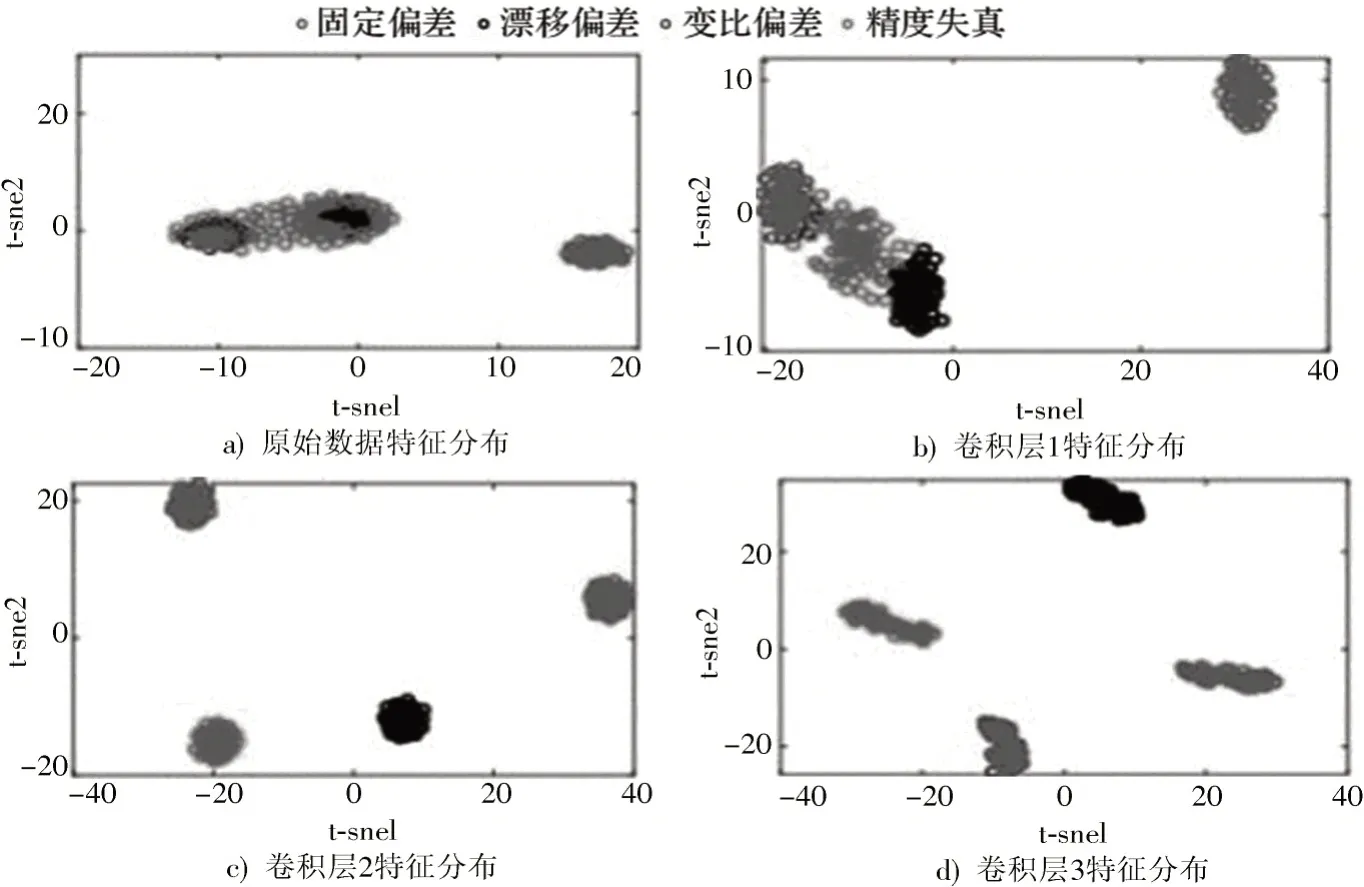
图11 通过t-SNE 实现特征可视化

图11 是原始数据输入后的可视化情况，由图可知，网络每层特征提取功能显著提高。结合原始数据分析，钳形电流互感器由于4 种故障所影响，最终通过杂乱的方式完成排序，网络层次持续递增时，单层网络特征提取水平也在提高，所以故障状态也需要保持独立。基于上述分析结果得出：训练好模型能保持较强的特征提取功能。

5 结 语

本文针对钳形电流互感器故障诊断率低的问题，提出一种基于VMD-SampEn-M1DCNN 组合模型的故障诊断模型。该模型将VMD 与SampEn 用于钳形电流互感器数据特征提取，通过构建具有多个一维卷积神经网络的集成网络模型——M1DCNN，将其用于样本数据训练和测试。

在实验中，一方面将VMD-SampEn-M1DCNN 模型与已有模型进行对比，证明该模型在训练时间、测试时间、检测准确度等方面都要比其他模型更好；另一方面，通过网络可视化对该模型的运行机制进行分析，证实模型具有较好的特征提取功能。