多重约束下智慧仓储搬运机器人移动路径选择研究

冯仁宇，夏 凯

（1.清华大学，北京 100091；2.上海外国语大学，上海 200082；3.上海烟草集团有限责任公司，上海 200082）

0 引 言

目前，智慧仓储中会使用大量搬运机器人完成搬运工作，以提高工作效率[1]。随着搬运机器人的广泛应用，人们对其智能性的需求越来越高，其中最基本的需求就是能自动选择路径完成搬运任务[2-4]。目前，已经有很多专家学者研究了搬运机器人路径选择的方法。例如，曹凯等人通过涡流约束法建立斥力场，按照梯度方向产生涡流场，通过涡流人工势场在涡流场内生成轨迹树，并提出轨迹树内的冗余节点，从而完成了搬运机器人路径的选择。该方法能够有效地选择路径，并且路径选择的收敛速度较快[5]。魏博等人将离子运动算法引入到人工蜂群算法中来改进算法，从而加快算法的收敛速度，并通过改进后的人工蜂群算法实现了搬运机器人路径的选择。该方法能够实现较快的路径选择，具备较高的效率[6]。但这两种方法均未考虑搬运机器人之间的路径冲突问题，容易发生路径冲突，且避障能力较差。在实际智慧仓储环境下，需要考虑多重约束条件，为搬运机器人选择一条最佳移动路径，并解决路径冲突问题，以提升搬运机器人的避障能力[7]。因此，需要研究多重约束条件下智慧仓储搬运机器人移动路径的选择方法，以缩短搬运机器人的运行时间和运行距离。

1 搬运机器人移动路径选择

1.1 移动路径选择函数

以智慧仓储搬运机器人运行长度f1(R)、运行困难指数f2(R)与运行时间f3(R)为目标函数，建立智慧仓储搬运机器人路径选择函数。

针对智慧仓储中搬运机器人运行长度这一目标函数f1(R)，假设搬运机器人可用移动路径为R={r1,r2,…,rn}，可用移动路径节点数量为n。f1(R)的计算公式如下：

式中：ri、rj分别表示可用路径上的第i、j个节点；d(ri,rj)表示ri与rj之间的距离。

针对搬运机器人经过路径内各节点的困难指数总和f2(R)，其计算公式如下：

式中：g(ri)表示搬运机器人经过ri时的困难指数；zi表示指定时间窗内，经过任一节点上的机器人数量。

针对代表智慧仓储搬运机器人的运行时间这一目标函数f3(R)，其计算公式如下：

式中：A表示智慧仓储内搬运机器人数量；xarij表示搬运任务数量；表示机器人经过节点i至j间直线路段需要的时间表示经过节点i至j间拐弯路段需要的时间；wij表示节点i至j间路段权重；tw表示时间窗。

的计算公式如下：

式中：vs表示搬运机器人匀速行驶速度；L(i,j)表示i与j间的距离；Lv表示搬运机器人长度。

的计算公式如下：

式中：vc表示搬运机器人拐弯行驶速度；Rtc为机器人的转弯半径。

综合f1(R)、f2(R)、f3(R)，建立智慧仓储搬运机器人路径选择函数，公式如下：

1.2 搬运机器人移动路径选择函数约束条件

第1.1 节建立的搬运机器人移动路径选择函数的多重约束条件如下：

1）搬运机器人搬运任务约束

智慧仓储中，任一搬运机器人只能执行一个任务[8]，公式如下：

式中：rij表示节点i至j间的路径。当xarij= 1 时，说明机器人a在路径rij上；当xarij= 0 时，说明a不在路径rij上。

2）时间窗约束

搬运机器人a在路径rij上的时间窗tw约束为：

3）时间窗内搬运机器人数量约束

移动路径上，指定时间窗内搬运机器人的数量约束为：

式中：表示由i移动至j的搬运机器人数量表示j移动至i的搬运机器人数量代表时间窗内机器人a经过rij代表时间窗内机器人a经过rji。

4）指定时间窗内，路径中搬运机器人数量约束

在内，rij上搬运机器人数量的约束为：

1.3 搬运机器人移动路径选择函数求解

利用改进的遗传算法，结合1.2 节中的约束条件，求解1.1 节建立的搬运机器人移动路径选择函数，并得到最短的运行长度、最低的运行困难指数和最短的运行时间，以及对应的移动路径选择结果。改进遗传算法中对适应度函数k进行改进，解决路径冲突问题，提升搬运机器人的避障能力，具体步骤如下：

步骤1：分析搬运机器人搬运物体与障碍物是否处于同一位置[9]，即，其中，分析搬运物体与障碍物是否处于同一位置时的适应度函数为ω2；当搬运物体位置k的适应度函数Fk为1 时，说明搬运物体与障碍物处于同一位置[10]。

步骤2：计算搬运物体所在直线方程。

步骤3：计算障碍物各边所在直线方程。

步骤4：求解步骤2 与步骤3 的方程组，获取障碍物与搬运物体所处直线上的全部重合点。

步骤6：设计适应度函数F=ω1F1+ω2F2，其中ω1、ω2表示F1与F2的权值。

对遗传算法内的适应度函数进行改进后，利用改进遗传算法进行选择、交叉与变异操作，求解搬运机器人移动路径选择函数f(R*)，得到搬运机器人的最佳移动路径，实现多重约束下智慧仓储搬运机器人移动路径选择。

2 实验分析

以某物流公司的智慧仓库为实验对象，该仓库内共包含5 个拣选台、10 个充电站、400 个货架、20 个搬运机器人。搬运机器人的具体参数如表1 所示。

表1 搬运机器人具体参数

当该智慧仓储内包含2 个搬运任务时，则需2 个搬运机器人同时进行搬运任务，利用本文方法为这2 个搬运机器人选择移动路径，移动路径选择结果如图2所示。

当该智慧仓储内只有一个搬运任务时，则仅需一个搬运机器人进行搬运任务，利用本文方法为该搬运机器人选择移动路径，移动路径选择结果如图1 所示。

图1 搬运机器人移动路径选择结果

根据图1 可知，本文方法可有效地为搬运机器人选择移动路径，且选择的移动路径中，并不会与障碍物发生碰撞，说明应用本文方法选择的移动路径可提升搬运机器人执行搬运任务的安全性。

根据图2 可知，对于多个搬运机器人同时在智慧仓储内执行搬运任务时，本文方法依旧可以有效地为搬运机器人选择移动路径，两个搬运机器人在执行任务时均未与障碍物发生碰撞。实验结果证明：本文方法具备移动路径选择的有效性，可提升搬运机器人执行搬运任务时的安全性。

图2 多个搬运机器人的移动路径选择结果

当智慧仓储中8 个搬运机器人同时进行搬运任务时，利用本文方法为这8 个搬运机器人选择移动路径，8 个机器人移动路径选择的长度、困难指数与运行时间如表2 所示。

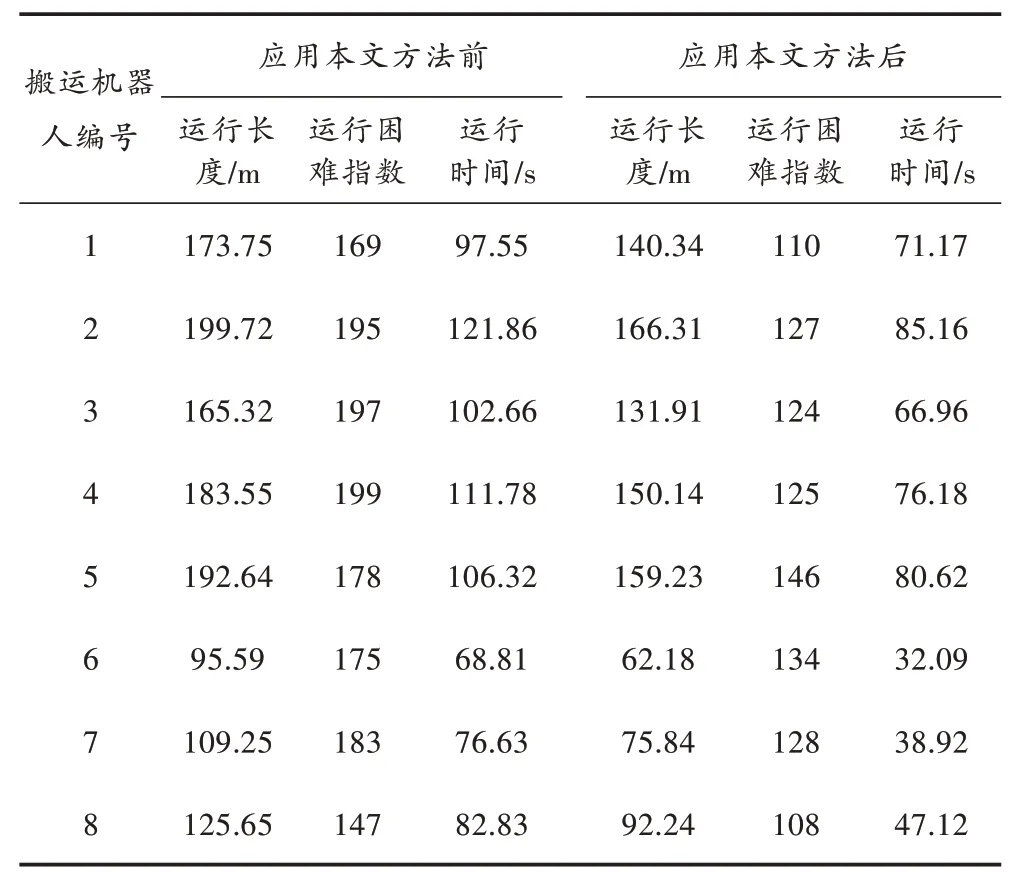
表2 搬运机器人的运行长度、困难指数与运行时间

根据表2 可知，应用本文方法前，搬运机器人的运行长度、运行困难指数、运行时间，明显高于应用后；应用本文方法前的平均运行长度是155.68 m，平均运行困难指数是180.38，平均运行时间是96.06 s；应用本文方法后的平均运行长度是122.27 m，平均运行困难指数是125.25，平均运行时间是62.28 s。实验结果证明：应用本文方法后，可有效减少搬运机器人的运行长度，降低运行困难指数，缩短运行时间。

3 结 论

未来物流行业的发展方向是智慧物流，而智慧物流的关键是智慧仓储，智慧仓储的关键则是搬运机器人。搬运机器人的移动路径选择效果直接影响智慧仓储的运营效率。因此，需要研究在多重约束条件下的智慧仓储搬运机器人移动路径选择方法，以提升搬运机器人的避障能力。