多策略改进蜉蝣算法的无人机航迹规划

席万强, 常保帅, 林思伟, 林俊志, 李 鹏,

(1.无锡学院,江苏 无锡 214000; 2.南京信息工程大学,南京 210000)

0 引言

近年来无人机行业发展迅速,其因代价低、操作方便等特点广泛应用于军事及民用领域。但无人机在低空飞行的安全性方面仍面临着巨大的挑战[1],而航迹规划是无人机能够平稳飞行、安全完成作业的基本保障,现已成为无人机研究的热门话题。

无人机航迹规划是指明确起点和终点,规划出一条无碰撞的、代价最优的无人机飞行路径。无人机航迹规划技术分为采样法、数学模型法、启发式函数法、深度学习法[2]。文献[3]提出了一种A*算法和DWA结合的方法,将弧形障碍物和凹形障碍物分别进行网格化预处理和凸形预处理后,改进A*算法的启发式函数,选取全局路径的关键点作为局部路径规划的子目标点,该算法缩短了航迹长度,提高了路径平滑度和安全性;文献[4]将调控力和检测因子引入人工势场法,解决了陷于局部最优和目标不可达的问题。上述两种方案在解决航迹规划时,计算复杂性高、收敛速度慢并且难以处理高维问题[5],而元启发算法可以产生更高质量的解,且易于实现。基于启发式搜索的路径规划包括粒子群算法、人工蜂群算法和布谷鸟算法等智能算法,是模拟自然界各种现象并求解最优化问题的算法。相较于其他策略的算法,群智能算法收敛稳定,能够找到满足要求的最优路径。文献[6]提出了一种新的球形向量粒子群优化算法,将搜索空间从笛卡尔空间切换到配置空间,在配置空间中获得高质量的解,提高了算法的效率和性能;文献[7]利用估计分布法提出了一种具有紧致格式的布谷鸟算法,并在此基础上采取并行通信策略,能有效地保存无人机的存储空间,提高执行效率。

蜉蝣算法(MA)[8]是基于雌性和雄性蜉蝣的飞行和交配繁殖等行为提出的一种新型智能算法,具有较强的局部收敛和全局开发的能力。文献[9]采用指数递减惯性权重(EDIW)策略、自适应柯西变异和改进的交叉算子对蜉蝣算法进行改进,高效地搜索无人机配置空间,发现总代价最低的路径。虽然上述改进算法被证明是有效的,但是仍存在执行效率低和解的质量不高等问题,且无法平衡全局搜索和局部开发之间的关系。

针对上述研究不足,本文采用莱维(Lévy)飞行对蜉蝣算法进行初始化,提高物种的多样性,充分搜索解空间。为解决陷入局部最优的问题,采用自适应t分布方法,并提出一种基于Pareto原理[10]的精英保留策略,以此增加系统的稳定性。最后,使用三次B样条曲线对路径进行拟合,生成平滑且稳定的轨迹。

1 数学模型建立

1.1 环境模型

使用仿生算法进行无人机三维路径规划,首先要对环境和障碍物进行建模,建立适应度函数,进而规划出最优路径;其次使用三次B样条曲线生成平滑的路径,在三维空间中一个蜉蝣粒子代表一条路径。假设一条路径包含n个航迹点,粒子的位置Xi=(xi1,xi2,…,xin)。基准地形和障碍物地形[11]分别为

(1)

(2)

式中:Z1是平面点对应的高程值[12];x和y为模型在平面上的点坐标;A,B,C,D,E,F,G为常系数,对高程地图中的山峰特征进行控制;(xi,yi)和hi分别为第i座山峰中心坐标值和山峰的高度;xsi和ysi控制第i座山峰的坡度。图1所示为环境三维图。

图1 环境三维图Fig.1 Three-dimensional map of the environment

1.2 代价函数

在航迹规划中,路径的长度、高度和偏转角都是衡量路径质量的重要因素,代价函数与两个相邻航迹点之间的距离、高度和偏转角有关,其综合代价为

F=min(D′+H+θ)

(3)

式中:F为适应度函数;D′为路径的总长度;H为路径的平均高度;θ为偏转角。算式分别为

(4)

(5)

(6)

其中,pi=(xi+1-xi,yi+1-yi,zi+1-zi)。

2 蜉蝣算法

蜉蝣算法初始化随机生成两组蜉蝣,分别代表雌性和雄性种群。

2.1 雄性蜉蝣飞行

雄性蜉蝣会聚集在一起,根据个体和群体经验来调整飞行方向。第i只雄性蜉蝣在d维空间的位置和速度分别可以表示为xi=(xi1,xi2,…,xid)T,vi=(vi1,vi2,…,vid)T。其位置更新可表示为

(7)

式中,k为迭代次数。

在实际生活中,雄性蜉蝣会在水面上几米的地方表演婚礼舞蹈。假设它们保持低速运动,则雄性蜉蝣i的速度为

(8)

(9)

gbest=min{f(pbest1),f(pbest2),…,f(pbestN)}

(10)

其中:N为群中雄性蜉蝣总数。式(8)中rp是xi和pbesti之间的笛卡尔距离;rg是xi和gbest之间的笛卡尔距离。这些距离为

(11)

最好的雄性蜉蝣会进行独特的婚约舞步,以不同的速度进行上下运动。这些雄性蜉蝣的速度为

(12)

式中:d′为婚礼舞蹈系数;r表示0～1的随机值。

2.2 雌性蜉蝣飞行

与雄性蜉蝣不同,雌性蜉蝣不会成群聚集在一起,但是会向雄性蜉蝣移动。第i只雌性蜉蝣位置更新为

(13)

雌性蜉蝣飞向雄性蜉蝣繁殖后代,并根据和雄性蜉蝣的位置更新自己的飞行方向。雌性蜉蝣和雄性蜉蝣在互相吸引的过程中按照个体适应度排名相同的原则,雌性蜉蝣的位置会随着具有相同排名的雄性蜉蝣的位置而改变,即

(14)

式中:rmf是第i只雌性蜉蝣和第i只雄性蜉蝣之间的欧氏距离;ffl是一个随机游走系数,当雌性蜉蝣没有被雄性蜉蝣吸引时使用。

2.3 蜉蝣交配

根据雌性蜉蝣和雄性蜉蝣的排名,具有相同排名的雌性和雄性进行交配繁殖,并产生两个后代,后代的位置为

(15)

式中:L表示0～1范围的随机值;子代的最初速度设为零;mmale和ffemale分别表示雄性和雌性的位置矩阵。

2.4 婚约舞步和随机游走

婚约舞步和随机游走使算法进一步地局部搜索,但是固定的系数在迭代后期可能使蜉蝣迭代到更糟糕的位置。故使舞步系数和随机游走系数随着迭代次数减少,更新算式为

(16)

式中,δ是随机因子。

2.5 后代变异

为了处理过早收敛的情况,使算法搜索到空间之前从未访问的新区域,随机挑选子代进行正态分布的扰动变异,即

(17)

式中:σ为正态分布的标准差;Nn(0,1)为标准正态分布。

3 改进的蜉蝣算法(CMA)

3.1 莱维(Lévy)飞行策略

蜉蝣算法在初始化阶段随机生成蜉蝣位置,丧失了种群的多样性,而更新机制使蜉蝣朝向最优个体迭代发展,因此容易陷于局部最优,过早收敛。故提出一种Lévy飞行策略,对随机初始化后的种群进行扰动。Lévy飞行是一个经典的随机过程,具有大概率进行大步长的飞行,容易跳出局部最优[13]。Lévy飞行可以更全面地对解空间进行搜索,故使用Lévy飞行对初始化后的位置扰动,其位置更新算式为

(18)

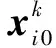
(19)

式中:β的范围是1≤β≤3,本文取1.5;u～N(0,σ2)σ和v～N(0,1)服从正态分布。σ的取值为

(20)

式中,Γ(·)是标准的伽马函数。

3.2 t分布策略

t分布又称学生分布,含有自由参数n,当t(n→∞)→N(0,1),当t(n→1)→C(0,1),其中,N(0,1)为高斯分布,C(0,1)为柯西分布,即标准高斯分布和柯西分布是两个边界特例分布[14]。t分布变异结合了柯西变异和高斯变异的特点,随着自由参数n的变化,算法可以进行不同程度的变异。

在蜉蝣种群中,雄性蜉蝣成群结对地进行游动更新,降低了整个蜉蝣种群的多样性,使用自适应t分布变异对雄性蜉蝣游动后的位置进行扰动,即在式(7)的基础上进行变异改进,更新位置为

(21)

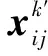
3.3 基于Pareto原理的精英保留策略

传统蜉蝣算法随机挑选子代进行变异,虽然增强了算法的随机性,但是大概率使蜉蝣后代陷入更糟的位置,导致算法优化结果较差,影响收敛速度。为了增强后代质量,提出一种精英保留策略,对子代的适应度按升序进行排名。使用优胜劣汰法则,对代价函数较低的子代进行变异,较高的保留,最后合并成新的子代,以保持种群的稳定性。在进化过程中要保证种群中解的精度和收敛效率之间的平衡[15],故提出一种基于Pareto原理(80/20法则)的精英保留策略,适应度排名的前20%保留,后80%变异。既有效地保持了种群的活力,又减少了数据冗余,提高了算法的运行效率。减少式(17)中子代变异的随机性。更新后的种群为

(22)

式中:m为子代种群数量;i为对子代按适应度排名后的第i只蜉蝣。式(22)的引入使子代不再进行随机变异,使算法跳出局部最优,增加物种多样性。图2为改进蜉蝣算法的流程图。

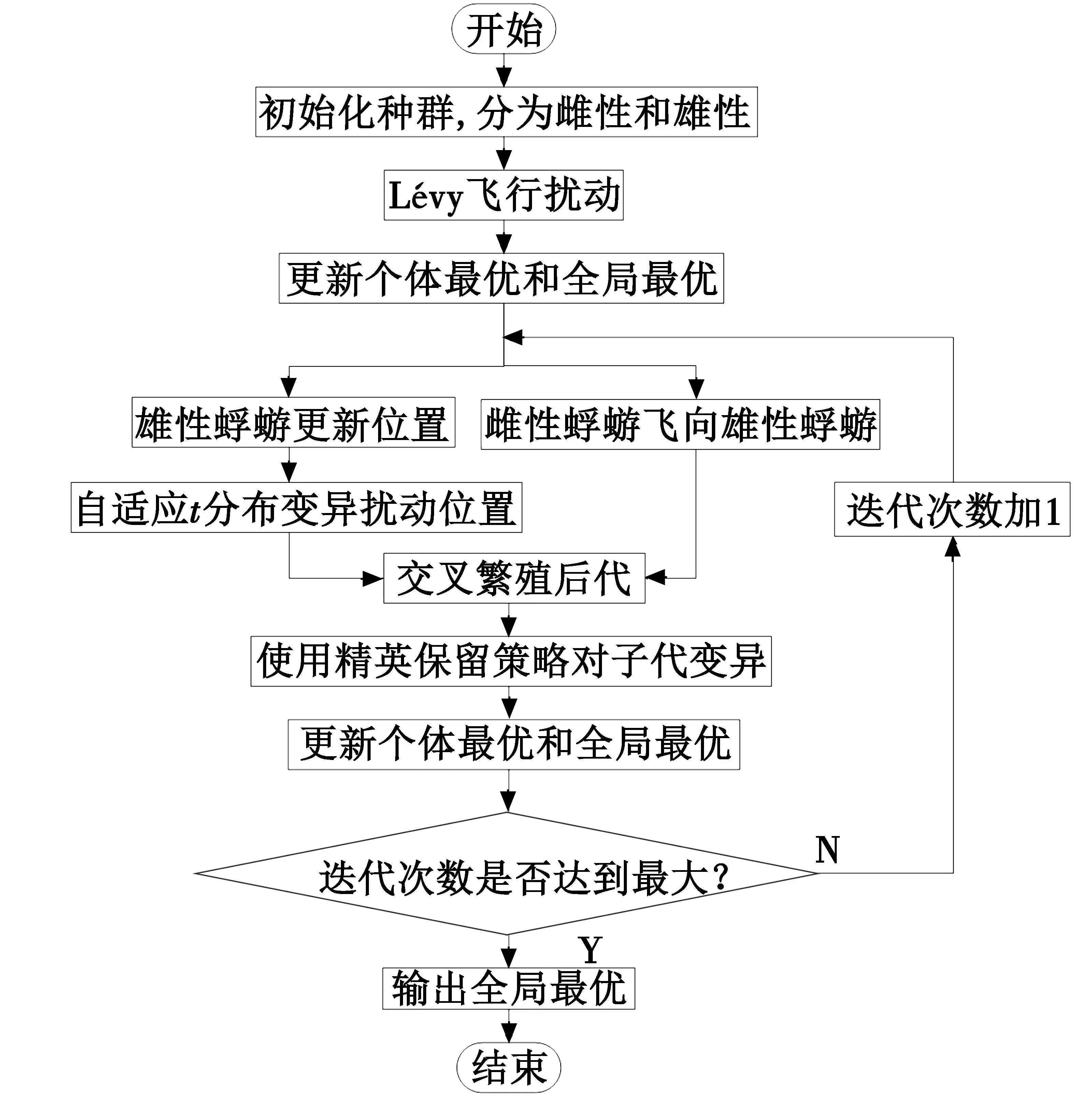
图2 改进蜉蝣算法流程图Fig.2 Flow chart of modified mayfly algorithm

4 仿真

本次仿真的地图搜索范围为100 m×100 m×100 m,使用式(1)、式(2)生成环境和障碍物模型。设置起始点为(1 m,1 m,1 m),目标点为(100 m,100 m,80 m),山峰数取6。算法中具体参数设置如下:重力系数取0.8 N/kg,游走系数ffl取1,舞蹈系数取5,游走迭代速率取0.8,舞蹈迭代速率取0.99。

表1显示了不同迭代次数对算法的影响,表中加粗数值表示3种算法中的最优值。在种群数量固定为50,迭代次数分别取100,200,500,独立运行算法30次的情况下,列出了3种算法的平均值(Mean)、最差值(Worst)、最优值(Optimal)以及标准差(Std)。从表1中数据可知,改进的蜉蝣算法(CMA)在迭代100次后就能找到较好的解,而传统的蜉蝣算法(MA)和粒子群算法(PSO)表现一般,且在后期容易陷入局部最优。虽然MA算法在30次运行中,适应度的最优值最小,但是标准差不如CMA,PSO的适应度平均值最差,在运行中容易产生震荡,故CMA算法在运行中更稳定。总之CMA在收敛速度与稳定性方面有显著优势。

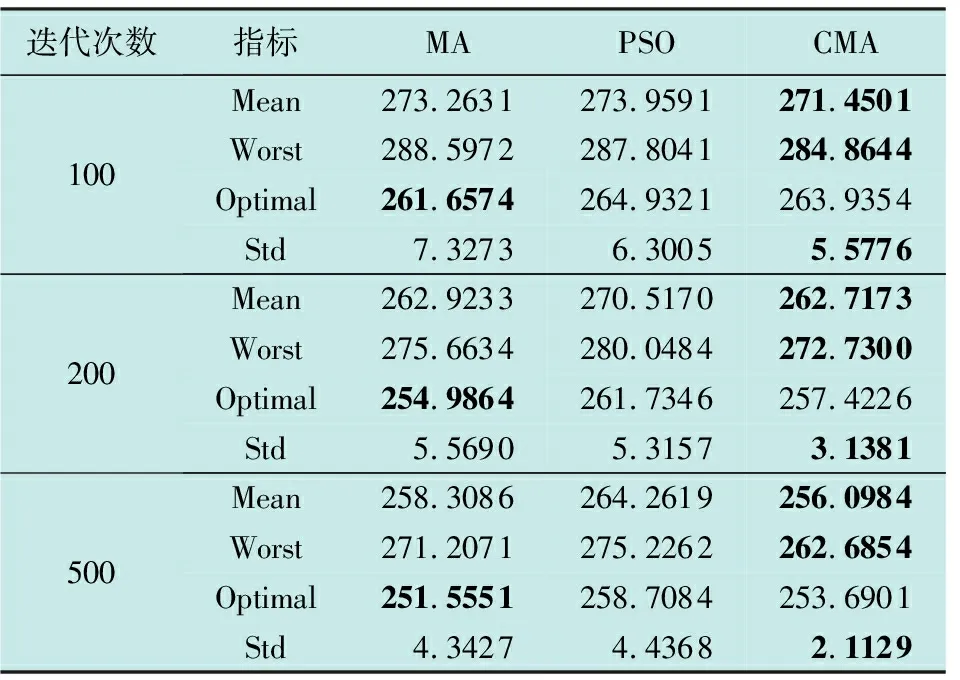
表1 算法性能测试比较

本文将改进蜉蝣算法(CMA)和传统蜉蝣算法(MA)放在同一复杂环境下进行比较。图3为航迹点n=5时3种算法在三维环境中的路径规划图。由图3可知,3种算法均能规划出安全无碰撞的路径,但是在路径的长度和平滑性方面有所不同,CMA规划的路径比MA和PSO路径更短、更稳定,MA会产生不必要的轨迹,导致距离变长,造成无人机电量的浪费。虽然PSO规划的路径长度比MA短,但是相较于CMA路径会产生冗余路径。在飞行过程中,CMA规划的轨迹,能在躲避障碍物的前提下匀速飞行,飞行高度逐渐上升,而MA和PSO规划的轨迹多处产生震荡,在轨迹初期飞行高度快速提升,接近终点时,降低高度,这种情况在实际应用中不可取,容易造成安全隐患,增大油耗。

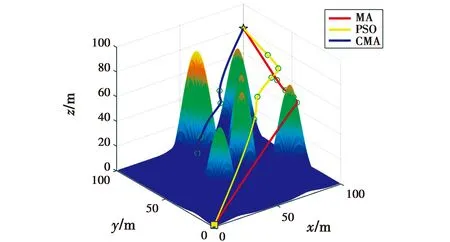
图3 3种算法的轨迹规划图Fig.3 Trajectory planning diagram of three algorithms

图4为3种算法的迭代收敛图,可以看出:在200次的迭代中,CMA更容易跳出局部最优,规划的路径更稳定且收敛速度快,前期就能找到比较优的路径,后期更容易找到全局最优;CMA在迭代200次后,其适应度优于MA和PSO,而CMA前期适应度高,路径多处震荡。PSO虽然前期就能找到适应度较好的位置,但是后期陷入局部最优。故CMA收敛速度更快,精度更高。

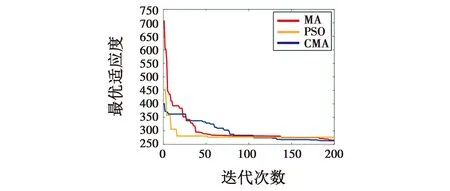
图4 3种算法的迭代收敛图Fig.4 Iterative convergence graph of the three algorithms

综上所述,CMA在进行航迹规划时,相较于MA和PSO,有收敛更加稳定、路径最短等优点,所以该算法可以作为一种有效的替代手段解决无人机路径规划问题。

5 总结

针对传统蜉蝣算法在进行无人机三维航迹规划中存在易陷于局部最优、不稳定和收敛速度慢等问题。本文提出一种基于多策略改进蜉蝣算法的无人机航迹规划,使用Lévy飞行、自适应t分布和基于Pareto原理的精英保留策略对其进行混合改进。通过三次B样条曲线对路径进行拟合,建立以路径长度、转弯角以及高度作为标准的代价函数来评价路径的优劣。为证明改进算法的有效性,在迭代次数不同的情况下将改进的蜉蝣算法、传统的蜉蝣算法和粒子群算法进行测试比较,并将其应用于无人机三维航迹规划,结果显示,改进的蜉蝣算法在收敛速度和精度等方面均优于传统蜉蝣算法和粒子群算法,规划出的航迹比较稳定且质量较高。