基于对抗训练的伪标签约束自编码器

富 坤，孙明磊，郝玉涵，刘赢华

（河北工业大学 人工智能与数据科学学院，天津 300401）

0 概述

现实世界中存在着大量的图结构数据，如引文网络、社交网络、蛋白质相互作用网络等，研究和挖掘网络深层的信息具有重大的意义。网络表示学习［1］是研究图结构数据最常用的方法，其目的是学习网络顶点的潜在、低维表示，同时保留网络拓扑结构、顶点内容和其他边信息，之后这些作为节点表示的向量就可以应用到后续的任务场景中，如节点分类、链接预测、社区发现、推荐系统等任务。

由于现实中的网络节点存在着标注缺失、标注错误和人工标注成本高的现象，因此监督或半监督的网络表示学习受到了很大的限制。为了解决这一问题，图自监督学习从数据本身自动获取监督信息，而不需要手动标注，这样模型就能够从未标记数据中学习更多的信息，从而在各种下游任务中表现出更好的性能［2-4］。图自编码器是一种重要的自监督学习模型［5］，它利用输入数据作为监督，通过编码得到低维的中间表示层，然后表示层再由解码器重构输入数据。整个学习过程以输入数据作为监督信号，无需引入节点标签，因此，利用自编码器的自监督优势进行网络表示学习受到了广泛的关注。

图自编码器算法在下游的任务中被证明是有效的，但仍然有2 个重要的问题有待改进：

1）由于缺乏有效的约束，导致编码过程中隐含的类别信息丢失，影响模型的学习能力。对此，一个可行的解决办法是设计相应的约束模块，最小化原始数据的生成类别概率分布和网络表示的生成类别概率分布之间的距离，减少编码过程中造成的隐含的类别信息损失，从而使得网络表示在下游分类任务中表现出更好的性能。

2）图自编码器算法通过最小化输入和重构的距离构造目标函数，忽略了中间表示层的潜在数据分布，网络表示学习受限于原始数据的规模，在数据量相对较少时容易产生过拟合，导致模型泛化能力弱，在处理真实世界的稀疏网络和有噪声的网络数据时容易效果不佳。处理这个问题的方法是引入正则化约束，强制潜在空间服从特定的概率分布。AAE［6］、AFL［7］、ALI［8］、ARGA［9］利用对抗框架去解决这个问题，它们引入对抗网络去组织潜在空间，通过误差反向传播的方式使得潜在空间服从特定的先验概率分布，从而增强模型的泛化能力。

本文提出一种新的网络表示学习模型：基于对抗训练的伪标签约束自编码器（Adversarial Training based Pseudo Label Constraint Auto-Encoder，AT-PLCAE）。该模型能够充分利用网络中的结构和属性信息，减少编码信息损失，增强模型的泛化能力。本文主要工作如下：1）在自编码器的潜在空间设计一个伪标签约束模块，通过减小原始图的伪标签和网络表示的伪标签之间的距离来约束模型，引导模型有效地学习，减小编码过程中产生的信息损失；2）设计与伪标签约束自编码器相适应的对抗网络，组织表示的潜在空间结构，使得潜在表示后验分布与输入的特定先验分布相匹配，缓解过拟合问题，增强模型的泛化能力。

1 相关工作

基于生成方法的图自监督表示学习的思想源于自动编码器，通过编码器网络将数据向量压缩为低维表示，然后采用解码器网络重构数据向量，将输入数据作为监督信号，以输入数据和重构数据的距离（相似性）来衡量表示学习的成果。该方法不依赖于数据标签，而是从无标签的数据中学习到良好的表示，再应用到下游的多个应用场景中。根据重构的内容不同，基于生成方法的图自监督表示学习可分为属性生成和结构生成2 类。

常见的基于属性生成的图自监督表示学习方法有Graph Completion［10］、MGAE［11］、GALA［12］等。Graph Completion 掩盖部分结点的属性，采用GCN［13］进行编码，利用上下文信息（输入的拓扑结构和未掩盖的属性信息）恢复掩盖的节点属性，帮助模型学习到更好的特征表示；MGAE 将邻接矩阵和随机破坏的结点属性矩阵通过GCN 网络映射成重构的属性矩阵，通过多次输入不同的破坏节点属性矩阵，最小化结点属性矩阵和重构节点属性矩阵的距离偏差，以生成结构和属性融合良好的特征矩阵；GALA 提出一个完全对称的图卷积自动编码器，编码器执行拉普拉斯平滑，而解码器执行拉普拉斯锐化。通过训练这个拉普拉斯平滑-锐化图自动编码器模型，可以将输入图重建成原始的属性特征矩阵。

常见的基于结构生成的图自监督表示学习方法有SDNE［14］、GAE［15］、VGAE［16］等。SDNE 采用自 编码器重构拓扑结构，通过一阶相似度以及二阶相似度约束自编码器得到网络节点的表示。GAE 采用GNN［13，16-17］编码器 将原始 图映射 到潜在空间，然 后经由内积函数解码成重构邻接矩阵，最后应用均方误差最小化原始邻接矩阵和重构邻接矩阵的距离。VGAE 将变分自动编码器［18］的思想集成到GAE 中，它采用了一个基于推理模型的编码器，生成2 个并行输出层的均值和偏差，通过重采样技术得到潜在空间后验概率分布，再采用KL 散度来测量先验分布和后验分布的距离，从文献报道来看，GAE 和VGAE 在链路预测和图聚类任务上都取得了很好的结果。

2 本文方法

给定一个图G={V,A,X}，其中，V表示节点集合，n=|V|表示节点数量，A={0,1}n×n表示邻接矩阵，X∊Rn×D′表示输入节点的属性矩阵。AT-PLCAE 模型的目标是将G映射到低维空间，生成图的低维表示Z∊Rn×d，其 中，d为网络 表示矩 阵的维度且d≪D'。Z作为嵌入矩阵，能很好地保留拓扑结构信息和属性信息，并用于下游节点分类任务。

AT-PLCAE 由编码-解码阶段和对抗阶段组成，如图1 所示（彩色效果见《计算机工程》官网HTML版，下同）。编码-解码阶段的具体过程如下：首先，为了确保自编码器的重构信息能充分接近原始输入图的结构信息和属性信息，引入PPMI 矩阵来融合图结构信息和属性信息；其次，为了得到良好的网络表示层，采用编码器生成潜在空间，再经由解码器重构PPMI 矩阵，通过重构损失函数来优化潜在空间；最后，为了在编码过程中减少信息损失，在潜在空间设计一个伪标签约束模块，通过减小原始数据的伪标签和潜在空间数据的伪标签之间的距离来优化编码器。对抗阶段的具体过程如下：为了解决潜在空间缺乏组织性和产生过拟合的问题，引入对抗网络去组织潜在空间，使得潜在空间服从特定的先验概率分布。上述2 个阶段交替进行训练，从而优化整个模型，最终生成最优的潜在空间。

2.1 自编码器设计

自编码器设计由2 个部分组成：一部分为结构-属性融合矩阵，用于将图结构信息和属性信息统一到一个融合矩阵中；另一部分为伪标签约束自编码器，通过设计伪标签约束项来减小编码产生的信息损失。

2.1.1 结构-属性融合矩阵PPMI

为了充分利用结构信息和属性信息，将图的结构信息和属性信息融合到PPMI 矩阵，该矩阵融合了节点的高阶信息和邻域关联信息，并将稀疏的表示矩阵转化成信息率较高的高信息密度表示矩阵。在构建PPMI 矩阵时，先融合结构信息和属性信息，形成结构-属性联合转移矩阵；再通过随机冲浪算法形成共现概率矩阵；最后生成PPMI 矩阵。构建PPMI矩阵的具体步骤如下：

1）为了融合和平衡结构信息和属性信息这2 种信息源，根据DNRL［19］算法融合结构信息和属性信息的策略，生成结构-属性联合转移矩阵T，计算方法见式（1）：

其中：TA表示结构转移概率，TX表示属性转移概率，分别从结构和属性2 个角度描述从节点vi到节点vj的转移概率；超参数α用于调整结构转移矩阵和属性转移矩阵所占的比重，α越大，结构转移矩阵所占的比重越大，α越小，属性转移矩阵所占的比重越大。

2）为了有效捕获节点正确的上下文信息，克服随机游走过程中存在的步长限制问题，采用随机冲浪［20］策略生成共现概率矩阵P，计算方法见式（2）：

其中：每个实值表示第i个节点在k步转换后到达第j个节点的概率；P0为初始的单位矩阵；超参数β表示进行随机冲浪过程的概率，而随机冲浪过程返回到原始节点并重新启动的概率为1-β。

3）为了避免转移到次要节点的概率过大（这种情况会降低整体表示结构的准确性），根据点态互信息（PMI）矩阵［20］的原理对共现概率矩阵P进行归一化，计算得到PPMI 矩阵，计算方法见式（3）：

2.1.2 伪标签约束自编码器

编码器将PPMI 矩阵作为编码器的输入并生成潜在空间。生成的潜在空间分为2 个部分：一部分为标签隐藏层，该层主要反映节点的伪标签信息；另一部分为表示隐藏层，即嵌入矩阵Z。表示隐藏层经由解码器得到重构的PPMI 矩阵。通过最小化重构损失函数来训练编码器和解码器，得到优化后的表示隐藏层。

整个自编码器网络采用全连接网络，将PPMI 矩阵（用M表示）作为编码器的输入，生成标签隐藏层C=fc(M,θc)和表示隐藏层Z=fz(M,θz)。为了使2 个隐藏层承载不同的信息，在编码器的最后一层权重不共享，标签隐藏层采用Softmax 函数激活，表示隐藏层不激活，而其余层权重共享。然后由生成的表示隐藏层解码得到重构的PPMI 矩阵=g(Z,θg)，最后通过最小化输入数据和重构数据之间的距离进行优化，损失项计算方法见式（4）：

为了减小编码过程造成的隐含的类别信息损失，本文设计一个伪标签约束模块：应用一个生成器来生成表示隐藏层的伪标签，代表网络表示的类别概率分布，而标签隐藏层代表着输入数据的类别概率分布，这2 个概率分布都代表节点类别的概率分布，应属于同一分布，所以，当这2 个概率分布越接近，编码过程造成的隐含的类别信息损失会越少。

原始数据由编码器分别生成标签隐藏层C和表示隐藏层Z。原始数据的标签隐藏层C可以表示原始数据的伪标签Yc，再设置一个全连接神经网络生成器来生成表示隐藏层Z的类别Cz=fzc(Z,θz)，用来代表表示隐藏层的伪标签Yc。采用交叉熵损失项Lc来衡量这2 种标签的距离，见式（5）：

为了在模型训练过程中使2 个层的分类标签更接近，应该最小化交叉熵损失项Lc。

编码-解码阶段的最终目标是生成良好的表示隐藏层Z。为了达到这一目标，编码-解码阶段联合自编码器和伪标签约束模块同时进行学习，损失函数见式（6）：

其中：λ为超参数，用于控制自编码器损失项和伪标签约束损失项的比重。

2.2 对抗阶段

编码-解码阶段采用的是基本的自编码器模型，直接得到的表示隐藏层空间中缺乏可解释和可利用的结构，即缺乏规则性，易产生过拟合现象。为解决这一问题，模型生成的潜在表示后验分布应与输入的特定先验分布相匹配，从而有规则地组织隐藏空间的结构。变分自编码器（VAE）［18］通过使编码器生成隐空间服从一定概率分布，并在损失函数中添加一个正则项来调整隐空间概率分布的规则性。DNRL 算法和VGAE 算法均用VAE 进行降维，以特定概率分布组织潜在空间，取得了优于直接采用自编码器进行降维的效果。然而，VAE 仍然存在2 个固有的缺陷：1）只支持显性的概率分布形式，即必须给出精确的概率分布函数，无法从未知的数据中进行采样和学习隐性的概率分布；2）VAE 理论复杂，在实际的应用过程中存在变分下界，即VAE 最后的训练结果和预定目标存在偏差。

生成对抗网络（GAN）［21-22］是最近几年比较流行的生成网络，在编码-解码阶段增加对抗训练与VAE在目标上是一致的，均能保证模型生成的潜在表示后验分布与特定先验分布相匹配。同时在编码-解码阶段增加对抗训练与VAE 相比具有以下2 个优点：1）不同于VAE 需要获得先验分布的精确函数形式，GAN 可以从显性概率分布中采样，如标准正态分布，也可以从未知的数据中采样，生成隐性的概率分布；2）相比VAE，GAN 没有变分下界，如果鉴别器训练良好，那么生成器可以更好地学习到样本的分布。

GAN 模型可看作是2 个神经网络在进行一场“最大-最小”博弈。GAN 由2 个网络组成，一个网络是生成网络G，另一个网络是鉴别网络D。G的任务是从一个概率分布空间中生成负样本，同时混淆D，使其认为自己生成的样本为正样本。D的任务是区分输入的样本是由生成网络生成的负样本，还是实际存在的正样本。在不断地迭代后训练网络最终达到一种平衡，这时，D无法判断样本是来自生成网络还是实际存在的，G便可以生成符合先验数据分布的数据。GAN 的博弈过程可用式（7）［21］表示：

标签隐藏层作为原始数据的伪标签，用于标识节点类别，每个节点的类别可以通过一个K维的one-hot 向量来表示，因此，假定标签隐藏层C的概率分布应与0-1 分布相匹配。本文设计的第1 个生成对抗网络从0-1 分布空间中采样，采用全连接网络生成数据Gx～(0,1)(x)作为正样本。与其对抗的负样本来自自编码器生成的标签隐藏层C=fc(M,θc)，因此，生成器即为编码器fc(M,θc)，记为GA(M)。正样本和负样本经过鉴别器分别得到Dc(Gx～(0,1)(x)) 和Dc(GA(M))。当生成对抗网络收敛之后，自编码器生成的标签隐藏层的概率分布与0-1 分布相匹配。

表示隐藏层用于表示高维空间的结构信息和属性信息，其概率分布应为连续的实值。中心极限定理认为多个独立同分布的随机变量之和近似于正态分布，所以，对于概率分布未知的表示隐藏层，假定其服从正态分布是合理的。本文设计的第2 个生成对抗网络的生成器从高斯分布中采样，采用全连接网络生成数据Gx～Gauss(x)作为正样本。与其对抗的负样本为自编码器生成的表示隐藏层Z=fz(M,θz)，因此，生成器即为编码器fz(M,θz)，记为GB(M)。正样本和负样本经过鉴别器分别得到Dz(Gx～Gauss(x))和Dz(GB(M))。当生成对抗网络收敛之后，自编码器生成的表示隐藏层Z的概率分布与高斯分布相匹配。

在对抗阶段，无论是第1 个生成对抗网络还是第2 个生成对抗网络，生成器均定义为生成负样本的网络，即为编码-解码阶段中的编码器。对抗阶段的最终目标是通过对抗训练的方式训练出性能优良的编码器，使得编码器生成的标签隐藏层和特征隐藏层分别服从特定的概率分布，从而解决自编码器的潜在空间存在的无组织性和过拟合的问题。通过式（8）对对抗训练阶段的模型进行优化：

2.3 伪代码

AT-PLCAE 伪代码描述如下：

算法AT-PLCAE

3 实验

为了测试AT-PLCAE 模型的性能，将AT-PLCAE模型与基准方法在4 个引文网络数据集上进行比较，通过学习到的网络表示在下游任务的节点分类实验，验证该模型在网络表示学习方面的有效性。

3.1～3.3节分别介绍数据集、基准方法和实验的参数设置。3.4 节和3.5 节实施节点分类任务以及可视化，表明AT-PLCAE 模型进行节点分类任务的有效性。3.6 节进行消融实验，分析不同模块对模型产生的影响。3.7 节对低维嵌入表示维度和目标函数中的超参数λ进行敏感性分析。

3.1 数据集

本文应用4 个引文网络数据集来评估AT-PLCAE模型的表示学习能力，分别为Cora、Citeseer、Wiki 和Pubmed。Cora 数据集包含来自7 个类的2 708 篇机器学习论文以及5 429 篇链接，每个文档由一个1 433 维的二进制向量描述；Citeseer 数据集包含来自6 个类的3 312 个出版物和它们之间的4 732 个链接，每篇论文都用一个3 703 维的二进制向量来描述；Wiki 数据集包含来自19 个类的2 405 个文档和它们之间的12 761 个链接，该数据集的属性矩阵有4 973 列；Pubmed 数据集 包括来 自Pubmed 数据库 的19 717 篇关于糖尿病的科学出版物和44 338 个链接，分为3 类。该数据集中的每个出版物都由一个由500 个唯一单词组成的字典中的TF/IDF 加权词向量来描述。

3.2 基准方法

本文将提出的AT-PLCAE 模型与常用的基准方法进行比较，常用的基准方法主要有DeepWalk［23］、node2vec［24］、DNGR［20］、AANE［25］、GAE 和MGAE。

DeepWalk 算法通过随机游走的方式，充分利用了网络结构中的随机游走序列的信息，将未加权的图结构转换成反映图拓扑结构信息的线性序列的集合，然后利用Skip-Gram［23］模型学习顶点的低维表示。node2vec 模型将广度优先搜索和深度优先搜索引入随机游走序列的生成过程。DNGR 算法首先运用random surfing 方法获取网络的高维节点表示，然后使用去噪自编码器学习节点的低维表示。AANE则通过矩阵分解将节点的结构信息与属性信息结合在一起，利用矩阵分解来学习低维表示。GAE 为基于结构生成的自监督学习算法。MGAE 为基于属性生成的自监督学习算法。

3.3 实验设置

实验采用深度学习框架PyTorch0.4.1，编程语言为Python，解释器版本号为3.6.1。AT-PLCAE 模型中伪标签约束自编码器的编码器设置成3 层全连接网络，解码器设置成与编码器对称的3 层全连接网络。在对抗网络中，生成网络采用3 层全连接网络，判别网络采用3 层全连接网络。将模型学习率控制在0.001～0.01 之间，可以更好地训练模型。标签隐藏层表示的是原始数据的伪标签，因此，其维度等于节点的类别数，而表示隐藏层维度受网络层数、图规模等因素影响，通过实验分析将表示隐藏层维度设置为256 维。目标函数式（6）中的权重λ通过实验分析设置为0.1。

3.4 节点分类实验

节点分类是衡量网络表示学习算法的一个主要实验，本文随机抽取50%带标记的嵌入层特征作为训练集，剩下的50%未标记的嵌入层特征作为测试集进行下游的节点分类任务。本文节点分类器采用Logistic 分类器，将F1 分 数（包 括Mi-F1 分数和Ma-F1 分数）作为节点分类的评价指标。

为消除偶然误差的影响，对于每个数据集下的每种算法均取10 次实验结果的平均值作为最终的F1 分数，实验结果如表1、表2 所示，其中加粗数据表示最优值。

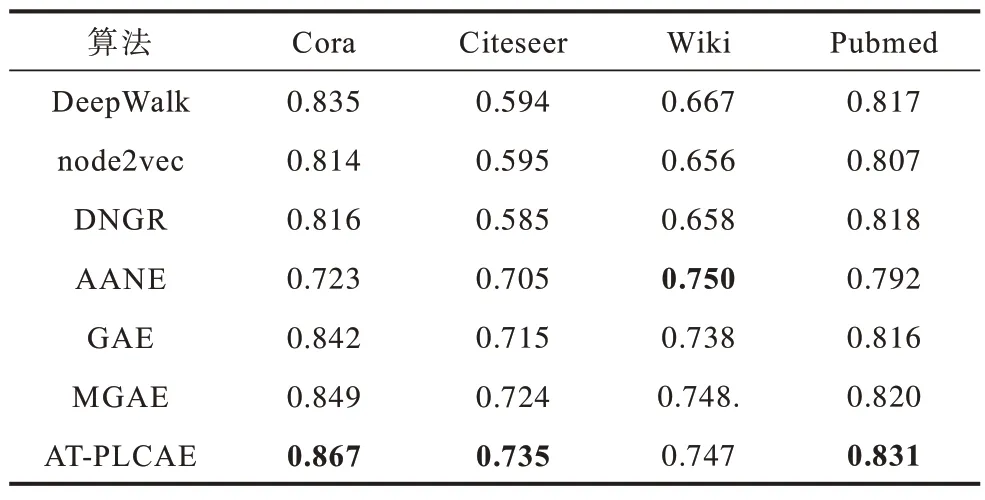
表1 各算法节点分类的Mi-F1 分数对比Table 1 Comparison of Mi-F1 scores of node classification of each algorithm

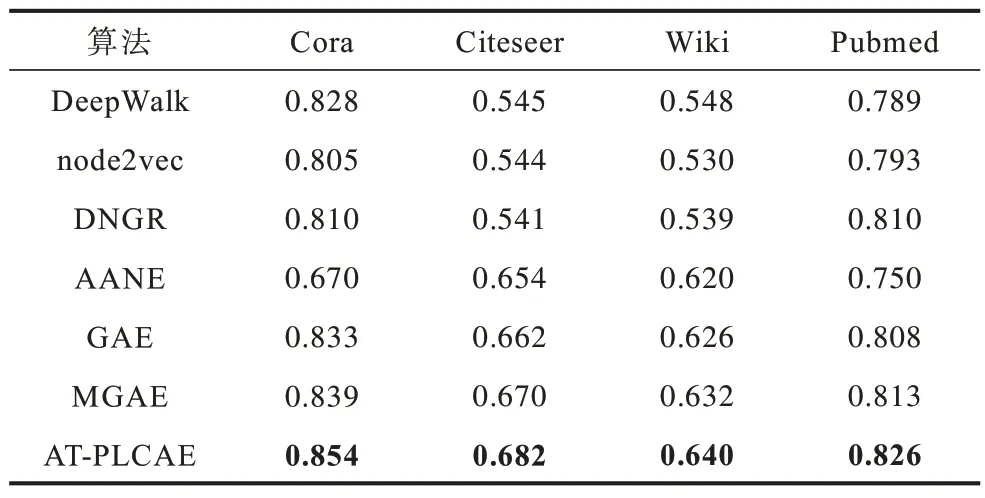
表2 各算法节点分类的Ma-F1 分数对比Table 2 Comparison of Ma-F1 scores of node classification of each algorithm

通过实验结果可以看出：AT-PLCAE 算法节点分类的Mi-F1 分数相对于基准方法的最高值，在Cora 数据集上超出0.018，在Citeseer 数据集上超出0.011，在Wiki 数据集上低0.003，在Pubmed 数据集上超出0.011；AT-PLCAE 算法节点分类的Ma-F1 分数相对于基准方法的最高值，在Cora 数据集上超出0.015，在Citeseer 数据集上超 出0.012，在Wiki 数据集上超出0.008，在Pubmed 数据集上超出0.013。由此可见，在节点分类任务上，AT-PLCAE 算法性能优于基准方法。

AT-PLCAE 算法在融合结构信息和属性信息时采用的PPMI 矩阵是基于随机冲浪策略的，虽然随机冲浪能克服随机游走有限步长的问题，但有限次随机冲浪确定的节点的转移概率在边数与结点数比值变大的情况下，不确定性和复杂性会增加。从本质上来，随机冲浪采样得到的概率仍是对局部拓扑结构的表示更有效，而不利于全图信息表示。AANE是一种基于矩阵分解的算法，更关注全局信息。当边数与结点数的比值变大时，则增加了全局信息，AANE 算法的性能会明显提升。采用E/N 来表示边数与结点数的比值，Wiki 数据集的E/N 为5.31，而Cora 数据集、Citeseer 数据集 和Pubmed 数据集 的E/N 分别为2.00、1.43 和2.25。相对于Cora 数据集、Citeseer 数据集 和Pubmed 数据集，Wiki 数据集 的E/N 更大。从实验结果中可以看出：AANE 算法节点分类的准确率随着E/N 的增大而增大；而AT-PLCAE算法在节点数相差不大的情况下，E/N 增加会使得算法节点分类的准确率降低。所以，在Wiki 数据集上，AT-PLCAE 算法节点分类的表现不如AANE算法。

3.5 可视化实验

分别采 用DeepWalk 算 法、AANE 算 法、DNGR算法和AT-PLCAE 算法得到Cora 数据集的网络表示，表示层的维度为256 维，然后采用非线性降维技术tSNE 算法将表示层维度降至2 维，进行可视化显示。从图2 中可以看出：由于AANE 是基于矩阵分解的算法，更关注全局信息，因此节点可视化分布发散，边界不够清晰；而DeepWalk 采样过程基于随机游走的策略，DNGR、AT-PLCAE 的采样过程基于随机冲浪的策略，相对于AANE 更容易提取局部拓扑结构信息，更关注节点的局部信息，所以，节点可视化分布较为聚集，边界较为清晰。

图2 Cora 数据集的表示层可视化图Fig.2 Visualization diagrams of presentation layer of Cora dataset

3.6 消融实验

AT-PLCAE 算法融合结构和属性信息，通过伪标签约束的自编码器学习到网络表示，并采用对抗网络组织潜在空间来增强模型的泛化能力。为了分析自编码器的伪标签约束项和对抗训练的不同组合对AT-PLCAE 模型表示学习能力的影响，应用PPMI+AE、PPMI+AAE、PPMI+VAE 和AT-PLCAE 模型来进行消融实验。这4 个模型均采用PPMI 模型作为输入，只是进行降维的方式不同，降维方式分别为自编码器（AE）、对抗自编码器（AAE）、变分自编码器（VAE）和伪标签约束对抗自编码器（GAAE）。其中：AE 为最基本的模型参照；AAE 用来说明对抗训练对模型产生的影响；为了说明对抗自编码器和变分自编码器组织隐藏空间的相似效果，采用VAE来进行实验；而AT-PLCAE 用以说明增加伪标签约束项对模型产生的影响。本节在4 个数据集上运用4 种模型学习低维嵌入表示之后，再进行训练集比例为50%的节点分类实验，采用F1 分数（包括Mi-F1 分数和Ma-F1 分数）作为评价指标。对于每个数据集下的每种模型，仍取10 次实验结果的平均值作为最终的F1 分数，实验结果如表3、表4 所示。

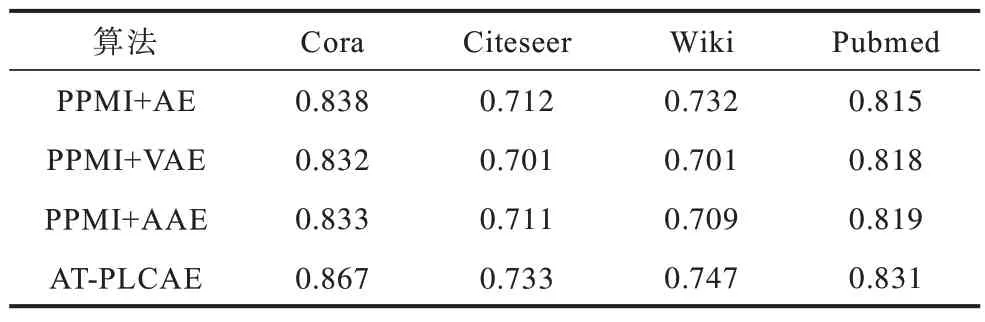
表3 AT-PLCAE 变体算法的节点分类的Mi-F1 分数Table 3 Mi-F1 scores of node classification of AT-PLCAE variant algorithms

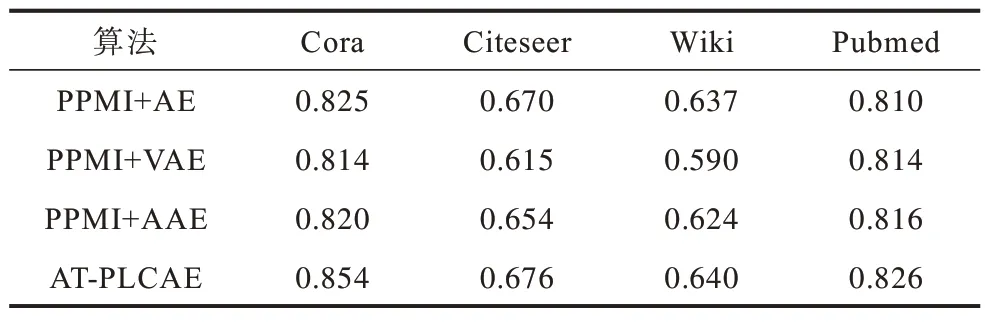
表4 AT-PLCAE 变体算法的节点分类的Ma-F1 分数Table 4 Ma-F1 scores of node classification of AT-PLCAE variant algorithms

通过实验结果可以得到以下结论：

1）PPMI+AE 在Cora、Citeseer 和Wiki 数据集 上的节点分类表现略好于PPMI+VAE 和PPMI+AAE，在Pubmed 数据集上的分类表现差于PPMI+VAE 和PPMI+AAE。VAE 算法指出由于在潜在空间增加噪音，使得潜在空间的特征表示由离散的单点变成连续的概率分布，这样在数据输入差异较大的情况下，模型也能生成稳定的特征表示。所以，这一现象的产生，很可能与PPMI+AE 出现了过拟合有关，自编码器生成的潜在空间是以离散的单点存在的，容易产生过拟合现象。

2）在4 个数据集上，采用对 抗PPMI+VAE 和PPMI+AAE 节点分类表现相近，AAE 算法证明了对抗自编码器与变分自编码器的强相关性，两者均能达到潜在空间以概率分布形式存在的目标，所以，这一实验结果说明这2 种方法具有相似的效果，同时相对于标准自编码器，采用对抗网络训练自编码器，增强了模型的泛化能力。

3）AT-PLCAE 在4 个数据集上的节点分类表现好于PPMI+AE、PPMI+AAE、PPMI+VAE，表明引入的伪标签约束项改善了模型性能，提高了节点分类准确率。

3.7 超参数分析

本节通过实验分析AT-PLCAE 模型中表示隐藏层的维数d和伪标签约束项权重λ对下游节点分类任务性能的影响。分析超参数时，在4 个数据集上先应用本文模型学习低维嵌入表示，再进行下游节点分类的实验，训练集比例为50%，评价指标为Mi-F1 分数，每个数据集仍取10 次实验结果的平均值作为最终的F1 分数。

分析隐藏层的维数d时，固定其他参数，分别设置d=64、128、256、512。从图3 中可以看出：4 个数据集d-F1 数值在d=128 时发生巨大转折，当表示隐藏层维度d低于128 维时，节点分类效果较差，所以，d的最低要求应为128；当d>128 时，d-F1 数值变化平缓，在d=256 时F1 值达到最大，即在表示隐藏层维度d=256 时，AT-PLCAE 模型性能最好。所以，完全考虑算法性能时，表示隐藏层维度取为256，同时考虑性能和内存要求时，表示隐藏层维度可取为128。

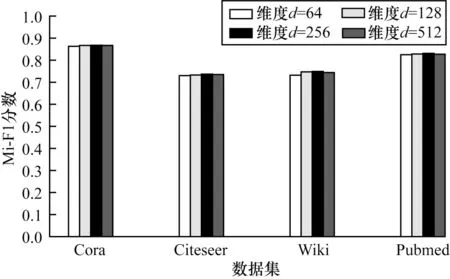
图3 表示隐藏层维度对算法性能的影响Fig.3 Infulence of representation hidden layer dimension on algorithm performance

分析伪标签约束项权重λ时，固定其他参数，分别设置λ=0.001、0.010、0.100、1.000。从图4 中可以看 出，Cora、Citeseer、Wiki 和Pubmed 数据集 在伪标签约束项权重λ=0.100 时结点分类F1 分数达到最大，所以，伪标签约束项权重λ=0.1，AT-PLCAE 模型在下游节点分类任务中性能达到最优。

图4 伪标签约束项权重对算法性能的影响Fig.4 Influence of pseudo label constraint weight on algorithm performance

4 结束语

本文针对图自编码器模型存在的信息损失和泛化能力差的问题，提出一个自监督学习的网络表示学习模型AT-PLCAE。该模型通过伪标签约束减少编码过程中的信息损失，同时采用对抗训练的方式隐性地组织隐藏层特征的概率分布，增强模型的泛化能力。在Cora、Citeseer、Wiki 和Pubmed 这4 个公开数据集上的节点分类实验表明，AT-PLCAE 的学习效果优于基准方法。在这4 个数据集上设计的消融实验表明伪标签约束项减少了自编码器编码产生的信息损失，改善了学习效果，提高了下游节点分类实验的准确率，同时针对伪标签约束自编码器的对抗训练增强了模型的泛化能力。

本文提出的框架仍存在以下问题需要解决：1）本文在PPMI 的基础上设计采样器，而采样的结果对于表示学习至关重要，需要设计能够保留更多和更准确原始结构信息的采样器；2）生成对抗网络存在收敛困难的问题。此外，本文实验采用最基本的生成对抗网络对整个网络进行训练和学习，无法知道对抗网络中的鉴别器和生成器是否达到最优，后续将设计相应的监测系统对每一部分的网络进行监听，用以评判整个网络的性能。