约减轮数分组密码LEA的差分分析
李艳俊 李寅霜 刘 健 王 克
①(中国电子科技集团公司第十五研究所信息产业信息安全测评中心 北京 100083)
②(北京电子科技学院 北京 100070)
1 引言
LEA算法[1]是2013年由韩国电子通信研究院(E lectronics and Telecomm unications Research Institu te,ETRI)提出的一个面向软件的轻量级分组密码,设计目标是在通用软件平台上提供快速加密。2017年,LEA被递交给国际标准化组织/国际电工委员会(International Organization for Standardization/International Electrotechnical Comm ission,ISO/IEC)作为轻量分组密码的候选标准,并且于2019年11月成为ISO/IEC国际标准轻量级加密算法。LEA的加密算法和密钥扩展算法中的模加、循环移位、逐位异或(m odu lar A dd ition,R otation,bitw ise XOR,ARX)操作可以有效并行实现,LEA不仅能够快速软件加密,而且代码量小。和高级加密标准(Advanced Encryption Standard,AES)等分组密码不同,LEA最后一轮的轮变换和其他轮一样,易于加密算法的软件和硬件实现。设计者认为有许多工作模式仅调用分组密码的加密算法,因此LEA不考虑加解密相似性,只强调加密算法的实现性能。LEA算法设计重点是循环移位数的选取,加密算法中3个移位数的选取策略使得扩散性和差分特征达到最优。LEA采用简单的密钥扩展算法,密钥字之间没有混合,只是对密钥字模加常数和循环移位,易于软件和硬件实现。
LEA算法基于ARX结构设计,该结构是对称密码设计中常用的一种设计方法,通过综合使用模加A(modular Addition)、循环移位R(Rotation)以及逐位异或X(Bitw ise XOR)3个操作来实现算法的非线性部件,进而达到混淆和扩散的作用,可以用来替换非线性部件S盒。基于ARX结构设计的分组密码有SPECK,HIGHT和Shadow[2–4]等。LEA是面向32 bit字的ARX类算法,分组长度为128 bit,密钥长度为128,192和256 bit,分别记为LEA-128,LEA-192和LEA-256,迭代轮数分别为24,28和32。
针对ARX结构分组密码的常用安全评估方法有差分分析[5,6]、差分线性密码分析[7,8]、积分分析、零相关线性密码分析等。文献[1]提出LEA算法的同时,也利用了多种分析方式对LEA的安全性进行了相关评估。2016年,文献[9]对LEA-128/192/256算法的零相关线性密码分析攻击提升到了9/13/14轮;同年文献[10]给出了数据复杂度为 296的7轮积分区分器;2018年,文献[11]利用混合整数线性规划(M ixed Integer Linear Program,M ILP)搜索给出了LEA-128的10轮零相关线性路线、10轮不可能差分路径;2019年,文献[12]利用M ILP和布尔可满足性问题(SATisfiability,SAT)方法分别得到了LEA-128的7/8轮积分区分器;2020年,文献[13]使用中间相错技术将LEA-128/192/256算法的积分分析攻击提升到了10/11/11轮;2022年,文献[14]对LEA算法进行差分与线性建模,通过拼接的方式得到了12 轮概率为2–107的差分线性特征。有关LEA-128的攻击分析结果比较如表1所示。
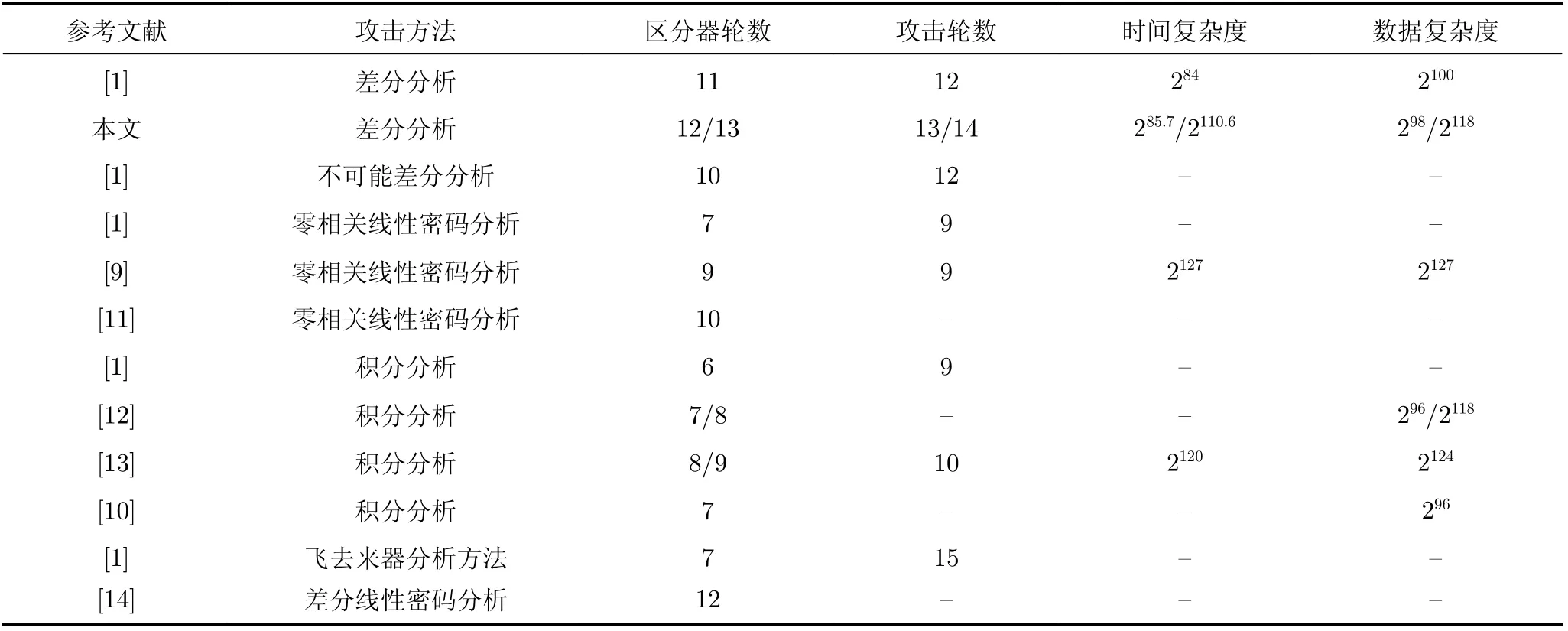
表1 LEA-128攻击分析结果比较
利用M ILP[15,16]工具可以找到LEA算法的12轮和13轮差分特征,从而计算出其对应的差分概率。基于此差分特征,结合提前抛弃技术,本文首次给出了LEA算法的13轮和14轮的密钥恢复攻击,其中13轮攻击的数据复杂度和时间复杂度分别是298个选择明文和285.7次13轮解密;14轮攻击的数据复杂度和时间复杂度分别是2118个选择明文和2110.6次14轮解密。
2 LEA算法简介
2.1 LEA的加密算法
加密算法由r轮迭代运算组成,轮变换如图1所示。其中X i[j]表 示32 b it的字,R Ki[j]是轮密钥,+表示模 232加,R ORi表示循环右移ibit,R OLi表示循环左移ibit。
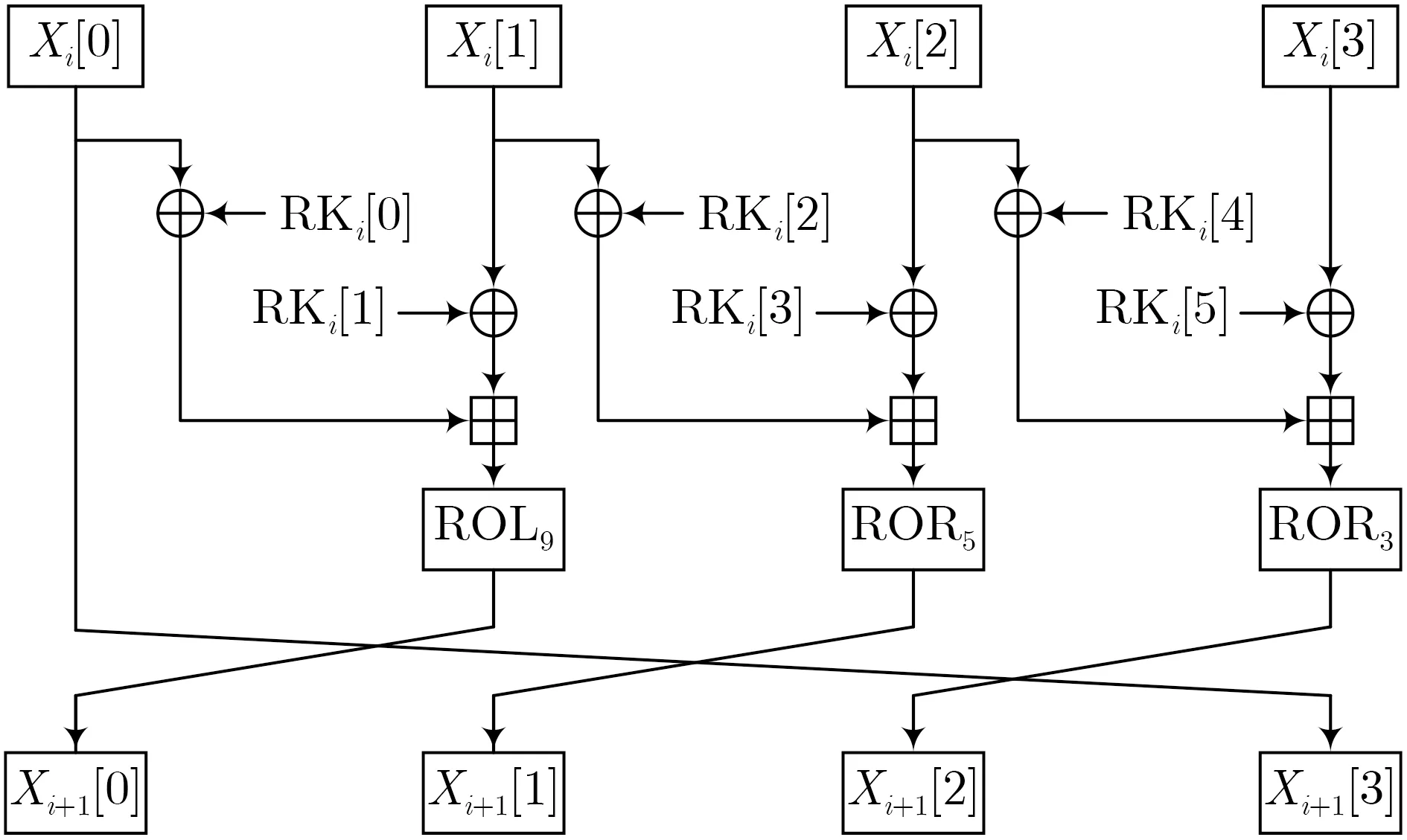
图1 LEA的轮变换
记128 bit的明文P=X0[0]‖X0[1]‖X0[2]‖X0[3],加密过程如下:
对i=0,1,...,r-1计算
X r[0]‖X r[1]‖X r[2]‖X r[3]=C为128 bit密文。
2.2 LEA的密钥扩展算法
LEA的密钥扩展算法需要8个32 bit常数,具体为
当密钥长度为128 bit时,K=K[0]‖K[1]‖K[2]‖K[3],令T[j]=K[j],0≤j ≤3。对i=0,1,...,23,轮密钥RKi=RKi[0]‖RKi[1]‖...‖RKi[5]如式(3)生成
当密钥长度为192 bit或256 bit时,具体的密钥扩展算法可详见文献[1]。
3 基于M ILP的ARX结构差分建模
在安全性评估方面,差分分析和线性分析仍然是最有效的分析方法,然而对于ARX结构的分析也不同于传统具有S盒的分组密码的分析。对基于字节或半字节设计的算法,通过搜索活跃S盒个数的下界可以给出差分特征估计;对基于比特设计的算法,文献[17]通过SAGE工具来产生刻画S盒差分分布特性的线性不等式集合,并用这些不等式来构建了搜索差分特征的M ILP模型;由于搜索程序是启发式的,得到的结果不一定为最优,为了克服这一问题,文献[18]提出了一种贪心算法,将启发式的搜索算法转变为准确且可以实际应用的搜索方法;对ARX结构算法,Lipmaa等人[19]基于M ILP工具给出了模加操作的差分特征刻画,并构建了自动化搜索模型,具体如下描述。
定义1模 2n加法输入差分为α,β,输出差分为γ,那么异或差分概率如式(4)计算
Lipm aa等人[19]提出先验证差分特征是否存在,再计算对应的差分特征概率,如下两个定理所示:
定理1模2n加法差分特征(α,β →γ)概率不为0当且仅当以下两个条件成立:
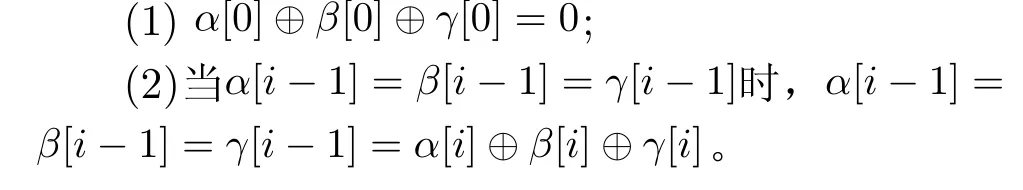

进一步,这5 个不等式等价于1 个等式:α[0]⊕β[0]⊕γ[0]=2d⊕,其中,d⊕是一个增加的比特变量。
下 面 用 向 量(α[i],β[i],γ[i],α[i+1],β[i+1],γ[i+1])刻 画第ibit与第i+1 bit差分之间的关系。文献[20]观察到根据定理1,这个向量只有56种可能的模式,加上变量¬eq(α[i],β[i],γ[i])形成7维向量,如图2所示。

图2 存在的差分向量模式
结合SAGE求解器和贪心算法[18],这56个向量可以由13个不等式来刻画,如图3所示。
对于两个输入变量和1个输出变量都为nb it的模加运算,共需要13×(n-1)+1个线性不等式来刻画,最后可以计算得到差分概率p=
4 差分概率与特征概率
为了精确评估分组密码在差分分析下的安全性,Lai等人[21]首先引入了马尔可夫密码理论,并对差分特征和差分进行了区分。在差分密码分析中,对于一个给定的输入输出差分值,可能存在许多潜在的具有相同输入输出差分的特征,它们对差分概率的大小都有贡献,这种效应被称作强差分效应[21],所以为了更加准确地计算差分概率,应当统计更多具有相同输入输出差分的特征。
4.1 计算差分概率

算法1 最优特征的差分概率
下面首先引入概率多项式的概念,它是差分概率的一种紧凑而简洁的表示形式,并给出了相应的特征。给定输入输出差分值的某一特定差分的概率多项式定义为:p(x)=p0x d+p1x d+1+p2x d+2+...,其中2-d是给定输入输出差分中概率最大的特征概率值,p i是具有概率为2-(d+i)的不同特征的数量,i=0,1,...,显然,通过计算x=时p(x)的具体值可以得到其对应特征的概率。特别地,可以考虑截断版的p(x),只包含前N个单项,即:
算法1显示了通过给定的原始M ILP模型如何构造最优特征的截断概率多项式。尽管在第(1)行中,M ILP求解器被配置为返回最优解以及变量的值,但在第(7)行中,它应该被配置为返回最优解的数量。
4.2 次优的解决方案
M ILP问题本质上是NP完全问题。因此,对于差分密码分析所对应的具有大量变量和约束的复杂的M ILP模型,M ILP求解器实际上是无法求得最优解的,所以一个次最优解就足够了。
为了找到次最优解,可以将r轮密码分成两个r1和r2轮子密码(r=r1+r2),分别独立求解。如果第1个和第2个子密码问题的最优值分别为d1和d2,则该密码问题的次最优值为d=d1+d2。通过算法1可以构造两个子密码问题的概率多项式p1(x)和p2(x)。为了推导r轮密码的概率多项式,需要结合r1和r2轮的每一个特征,考虑所有可能的r轮特征。这个过程完全等价于将两个子密码的概率多项式相乘。所以r 轮差分的概率多项式是p(x)=p1(x)p2(x)。
一般来说,实际的问题可能十分复杂,以至于把r轮密码分成两个子密码是不够的。因此,将r轮密码用概率多项式pi(x),i=1,2,...,k分成k个子密码。显然,第i个子密码问题的输出差分等于第i+1个子密码问题的输入差分。
最后,r轮密码的概率多项式可以表示为p(x)=,其中差分概率表示为
4.3 基于M ILP的差分概率
根据第3节描述的针对ARX结构差分分析的M ILP模型,可以构造一个针对任意轮的LEA密码的M ILP模型。但如果没有任何额外的约束来搜索r 轮LEA,当r ≥ 4时,M ILP模型将变得过于复杂而无法求解。因此,根据4.2节的分析,可以采用两个短的特征来构造一个长特征的方法。针对LEA-128,文献[22]给出了12轮和13轮的差分特征及计算其对应差分概率的方法。
4.3.1 12轮LEA差分分析
首先对12轮LEA进行分析,将其分为两个6轮的子密码问题,并且第1个子密码问题的输出差分与第2个子密码问题的输入差分相同。将这两个问题独立求解,找到d=d1+d2最小的特征,此时12轮内部的差分特征=(0x00000000,0x00000000,0x00000000,0x00020000)。在这种情况下,d1=70,d2=37。因此,对应的次最优12轮特征为d=107。这个特征的详细信息如表2所示。
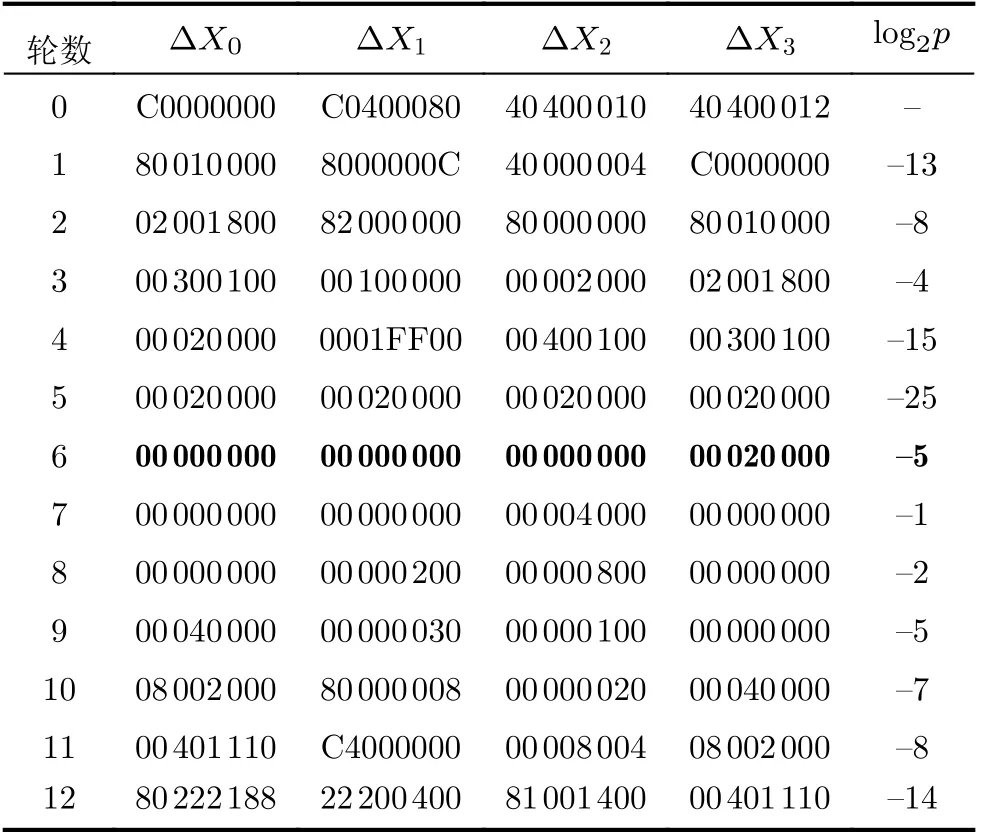
表2 LEA算法的12轮差分特征及概率
为了求次优特征对应的差分概率,首先根据算法1找到概率多项式p1(x)和p2(x)
可以计算出12轮差分的概率多项式如式(9)最后通过计算x=时的p(x)值,可以求得LEA 的12轮差分概率为
4.3.2 13轮LEA差分分析
由于7轮的M ILP问题不能较好地进行求解,所以将密码分成了3个子密码,前两个子密码是之前发现的两个6轮子密码,第3个子密码是1轮子密码,它的输入差分等于第2个子密码问题的输出差分,即=(0x80222188,0x22200400,0x81001400,0x00401110)。表3显示了特征的详细信息。
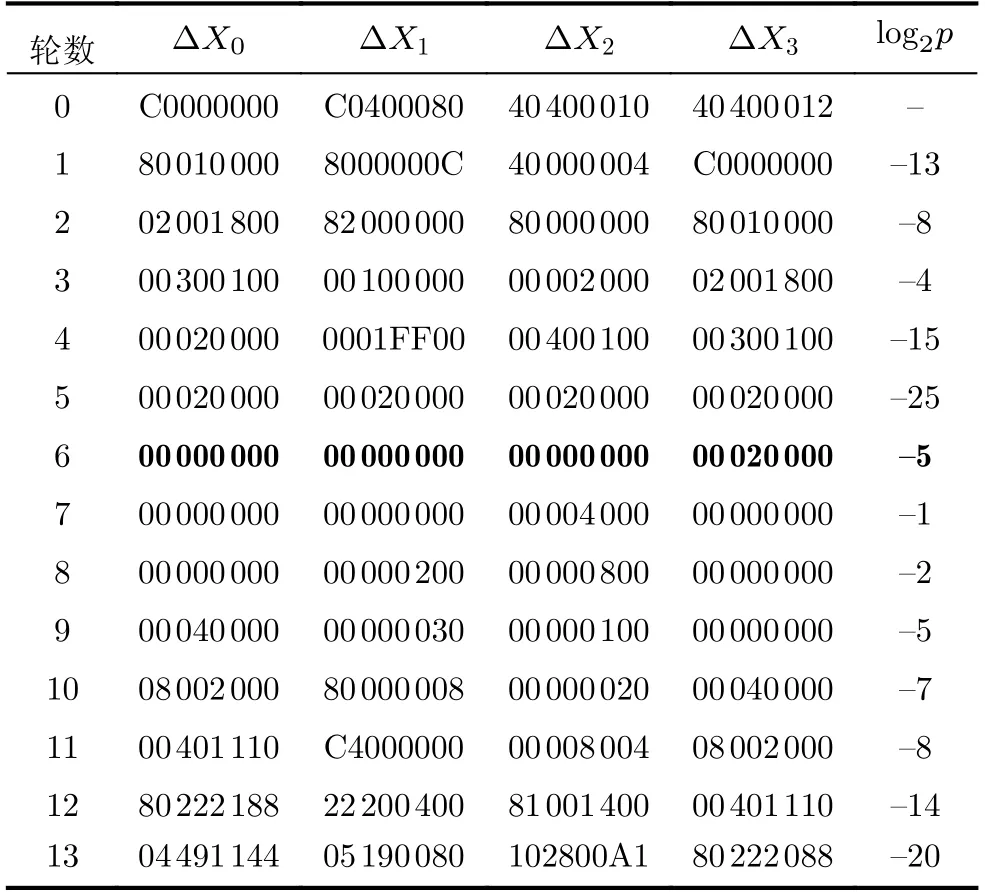
表3 LEA算法的13轮差分特征及概率
最后通过计算x=时p(x)的值,可以求得LEA的13轮差分概率为
5 密钥恢复攻击
5.1 13轮密钥恢复攻击
在以上12轮差分路径后加1轮,形成13轮如图4所示,为了更方便地描述解密过程,令X13[1]⊕RK13[1]=Y13[1], (X13[0]⊕RK13[0])⊞Y13[1]=Z13[1]。
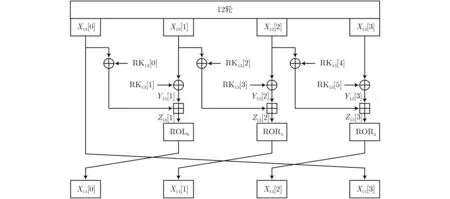
图4 13轮密钥恢复攻击
步骤1构造 2N个明文对,加密13轮,根据12轮输出差分特征,显然有ΔZ13[1]的低4位为1 000,ΔZ13[2]的 低11位全为0,ΔZ13[3]的低5位为10 000,由此可确定密文差分ΔX14[0]中有1 bit为1,3 bit为0; ΔX14[1]中有1 1 b i t 为0;ΔX14[2]中有1 bit为1,4 bit为0;并且ΔX13[0]=ΔX14[3],筛选后得到2N-4-11-5-32个密文对;
步骤2 猜测R K13[0]的 32 bit,解密得到ΔY13[1],其低4 bit差分值与RK13[0]的相应比特无关,所以过滤得到2N-52-28个对;
步骤3猜测 RK13[1]⊕RK13[2]的32 bit,解密得到ΔY13[2],其低11 bit差分值与RK13[1]⊕RK13[2]的相应比特无关,过滤得到2N-80-21个对;
步骤4猜测 RK13[3]⊕RK13[4]的32 bit,其低5 b it差分值与RK13[3]⊕RK13[4]的相应比特无关,过滤得到2N-101-27个密文对。
令N =97,对于猜测正确的96 bit密钥,平均剩下2个对;对于猜测错误的密钥,平均剩下2-31个对。
复杂度:第1步需要加密 298个明文,第2步进行232×245次1/3轮解密;第3步进行232×232×217次1/3轮解密;第4步进行232×232×232×2-4次1/3轮解密。所以数据复杂度为298个明文,时间复杂度为次13轮解密。
5.2 14轮密钥恢复攻击
在以上13轮差分路径后加1轮,形成14轮如图5所示,为了更方便地描述解密过程,令X14[1]⊕RK14[1]=Y14[1], (X14[0]⊕RK14[0])⊞Y14[1]=Z14[1]。
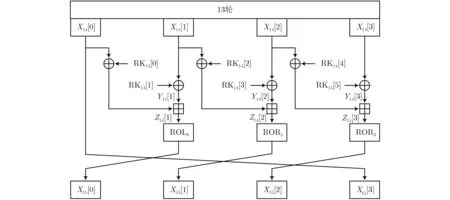
图5 14轮密钥恢复攻击
步骤1构造 2N个明文对,加密14轮,根据13轮输出差分特征,显然有ΔZ14[1]的低3 b it为100,ΔZ14[2]和 ΔZ13[3]的最低位都为1,由此可确定密文差分ΔX15[0]中 有1 bit为1,2 bit为0;ΔX15[1]中有1 bit为1;ΔX15[2]中 有1 bit为1;并且ΔX14[0]=ΔX15[3],筛选后得到2N-3-1-1-32个密文对;
步骤2猜测R K14[0]的 32 bit,解密得到ΔY14[1],其低3 bit差分值与RK14[0]的相应比特无关,所以过滤得到2N-37-29个对;
步骤3猜测 RK14[1]⊕RK14[2]的32 bit,解密得到ΔY14[2],其最低位比特的差分值与RK14[1]⊕RK14[2]的相应比特无关,过滤得到2N-66-31个对;
步骤4猜测 RK14[3]⊕RK14[4]的32 bit,其最低位比特的差分值与R K14[3]⊕RK14[4]的相应比特无关,过滤得到2N-97-31个密文对。
令N =117,对于猜测正确的96 bit密钥,平均剩下2个对;对于猜测错误的密钥,平均剩下2-11个对。
复杂度:第1步需要加密2118个明文,第2步进行 232×280次1/3轮解密;第3步进行232×232×251次1/3轮解密;第4步进行232×232×232×220次1/3轮解密。所以数据复杂度为2118个明文,时间复杂度为次14轮解密。
6 结束语
本文对LEA算法的抵抗差分分析能力进行了安全性评估,针对LEA-128算法,本文首次进行了13轮和14轮的密钥恢复攻击。为了减少攻击的计算复杂度和选择明文量,选择差分特征中概率最大的一条并计算其对应的差分概率,改进了文献[1]中的差分分析结果。攻击过程运用加密算法的部分特性,采用了提前抛弃技术,从而减少了密钥的猜测量,降低了计算复杂度,最终使得13轮密钥恢复攻击的数据复杂度为 298个明文,时间复杂度为286.7次13轮解密,使得14轮密钥恢复攻击的数据复杂度为2118个明文,时间复杂度为2110.6次14轮解密。
然而,如何优化建模实现对LEA-128概率更大的差分路径进行搜索,并采用合适的方法对其进行密钥恢复攻击则是本文下一步的工作。

