RGD及NLSY1伽马波段的流量分布及RMS-Flux关系研究

王 娜，易庭丰*，普治元，张 顺，王 亮，陈雨潼

(1. 云南师范大学物理与电子信息学院，云南 昆明 650500；2. 广西相对论天体物理重点实验室，广西 南宁 530004；3. 云南省中马HF-VHF先进射电天文技术国际联合实验室，云南 昆明 650216)

根据光度和发射线的性质，活动星系核(Active Galactic Nuclei, AGN)可以分为类星体(Quasi-Stellar Object)、赛弗特星系(Syfert)、低电离核发射线星系(Low-Ionization Nuclear Emission-line Region Galaxy, LINER)、射电星系等[1]。不同类型的活动星系核是由不同的吸积率和不同的视线方向导致的[2]。赛弗特星系相对类星体来说是一种低光度活动星系核[3]。窄线型赛弗特星系1是一类具有高度可变、相对较窄的发射线线宽(FWHM<2 000 km·s-1)和较弱的禁线([O III]λ5007/Hβ<3)的赛弗特星系，通常具有相对较低的黑洞质量和相对高的爱丁顿比[4-5]。活动星系核包括两个基本类型：射电噪活动星系核和射电宁静活动星系核。其中射电星系是射电噪活动星系核的一个重要子类，其喷流方向与我们的观测视线的夹角较大(一般超过10°)，喷流多普勒增亮效应也比较弱，往往展现出射电核加双边喷流的形态，是研究超大质量黑洞附近的喷流形成区和准直过程的理想目标源[6]。射电星系按照形态又划分为FR-I型和FR-II型两类。FR-I型星系的喷流光度较弱，呈现边缘昏暗型；FR-II型星系具有较高的喷流光度，呈现边缘增亮型[7]。

在过去30年里，γ射线天文学的发展已经成为研究活动星系核的光谱与时间行为的重要工具。费米望远镜的发射为我们探索射电星系和赛弗特星系的γ射线源提供了一定条件[8-9]。对活动星系核在γ波段的流量分布分析有利于理解喷流及等离子体加速，对探索和了解辐射过程也具有重要意义。流量的对数正态分布在星系和河外源中已经被发现，如X射线双星(X-Ray Binary, XRB)和活动星系核[10-14]。对于X射线双星，流量分布在亚秒级的时间尺度上呈对数正态分布，Seyfert 1 NGC 4051的X射线通量呈对数正态分布[10]。对于活动星系核来说，在几分钟到几天的时间范围内观察到Seyfert 1 IRAS 13224-3809的X射线流量呈对数正态分布[15]。对于耀变体(Blazar)来说，2009年在RXTE(Rossi X-ray Timing Explorer)的观测中，首次发现蝎虎座BL型天体流量分布的对数正态性[14]。Seyfert Galaxy NGC 4151光学通量与其相应变化之间存在线性关系，这反过来又表明流量分布的对数正态性[16]。此外，尽管数据是非连续的，但在超高能量(Very High Energy, VHE, >100 GeV)Mrk 421和Mrk 501中也发现了这种对数正态分布[17-19]。在Fermi-LAT观测到的最亮的耀变体γ光变曲线中也发现类似的趋势。长期流量分布的研究对于分析和表征天体物理光源的变化至关重要，近年来由于观测天体物理学的发展对长期流量分布提供了重要条件。

流量的对数正态分布意味着辐射是由乘法过程驱动而非加性过程[12]。在赛弗特星系和X射线双星等黑洞驱动源中，X射线流量分布的对数正态性被广泛认为是吸积盘波动的结果。因此，X射线的对数正态流量分布可能是受到吸积盘中调制的影响[20-22]。但是，γ波段辐射是相对论聚束的，那么类星体γ波段的流量对数正态分布可能是喷流的不稳定性，或者喷流几何结构变化和投影效应组合引起的。伽马射线源的对数正态流量分布不是由单一因素主导，而是源于多种相互影响因素，比如磁场能量密度、高能粒子密度以及种子光子密度等[23]。

本文利用费米卫星自2008年8月至2022年10月的γ射线光变曲线数据研究了射电星系和窄线型赛弗特星系1的流量分布特性，即流量分布及均方根-流量的关系。本文从费米大面积望远镜第四期目录中选取7个射电星系和6个窄线型赛弗特星系1作为样本，费米望远镜对这些源间隔3天的频率持续监测(>97%)为我们分析这些源的光变曲线(时间序列)提供条件。我们使用直方图、均方根-流量描述流量分布特征，并且对流量分布直方图进行高斯拟合及对数正态拟合。

1 样 本

2008年8月发射的γ射线空间望远镜(The Fermi Gamma-Ray Space Telescope)，以大面积望远镜(The Large Area Telescope, LAT)为主要载体。它提供了瞬态γ射线源几乎一致且连续的持续观测，具有最长且采样最均匀的γ射线数据。大面积望远镜的高占空比和长期监测使其成为研究时域天文学的重要工具，提供了数千个瞬态和可变光源的识别和定期观测，最新目录已经更新到4FGL-DR3[9]。4FGL-DR3中光变指数大于21.67的1 525个源包括7个射电星系和6个窄线型赛弗特星系1。其中包括以3天、1周、1个月为间隔的数据，我们选择从2008年8月至2022年10月以3天为时间间隔且最小检测显著性为4(2σ)的光变曲线作为研究对象，它们为流量分布和均方根-流量关系的研究提供了更多数据。

2 流量分布研究

流量数据的直方图可以表征流量的分布，它是流量分布可视化的重要工具。图1展示了射电星系和窄线型赛弗特星系1的流量分布直方图。大部分直方图显示一个突出峰值和高流量尾部。为了进一步理解分布情况，我们对流量分布直方图进行高斯拟合和对数正态拟合。除了直方图可以判断分布特性之外，我们还对流量的正态性和对数正态性分别进行了K-S检验、S-W检验以及计算约化卡方。如表1，结合K-S检验和S-W检验结果我们可以看到，无论是射电星系或者是窄线型赛弗特星系1的流量分布都拒绝了正态分布，他们的流量分布更加服从对数正态分布。结合约化卡方也可以看到，这两种的流量分布更加服从对数正态分布。

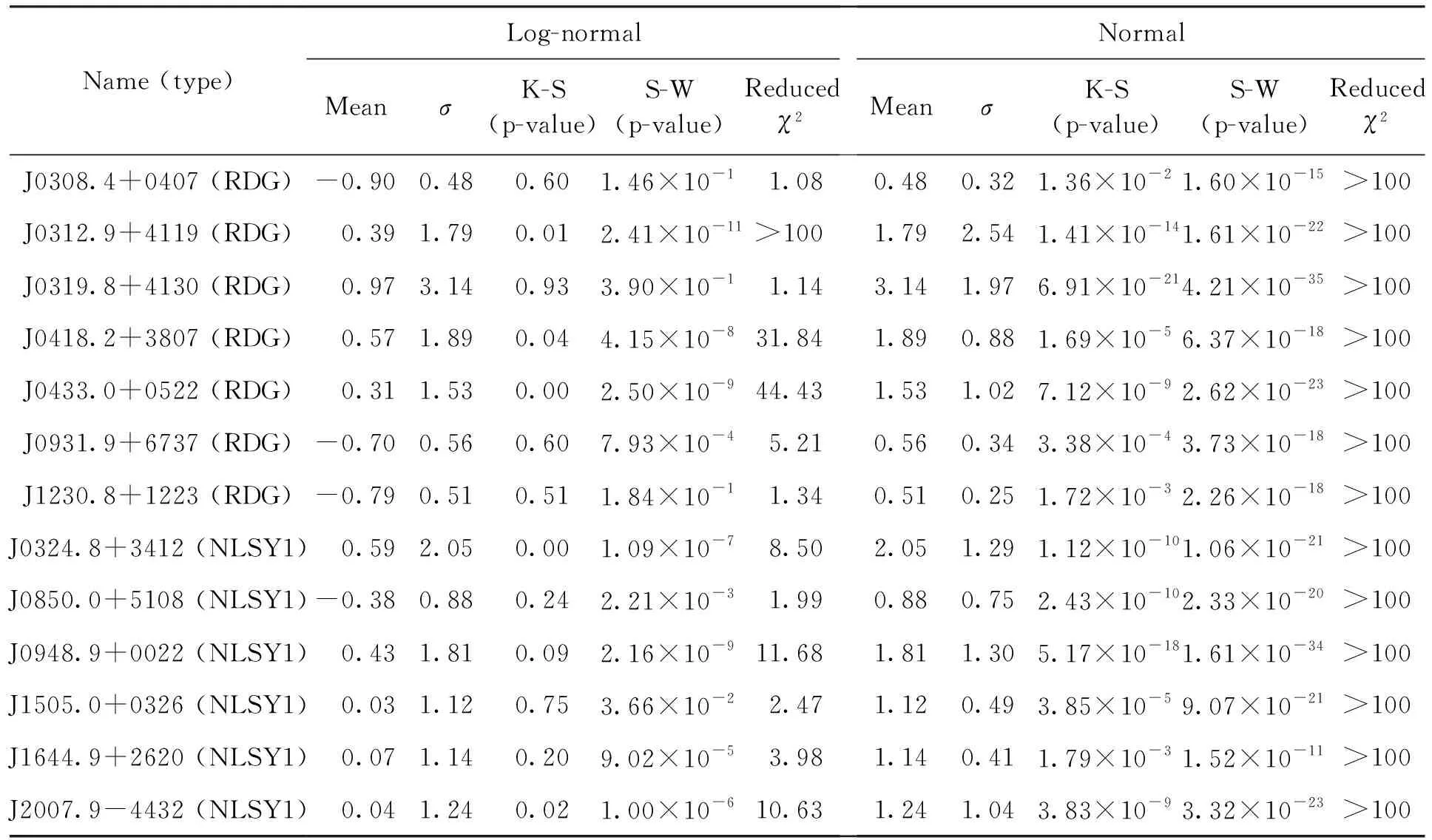
表1 射电星系和窄线型赛弗特星系1的γ射线通量分布的对数正态和正态分布拟合参数Table 1 Log-normal and normal distribution fitting parameters for the gamma-ray flux distributions of RDG and NLSY1

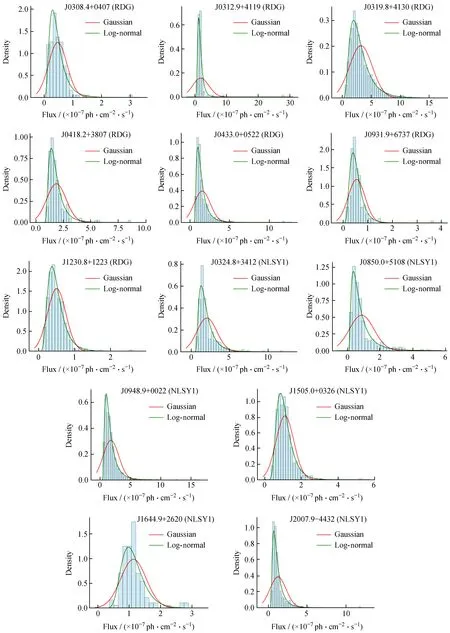
图1 4FGL γ波段射电星系和窄线型赛弗特星系的流量分布直方图(图中红色线代表高斯拟合，绿线代表对数正态拟合)Fig.1 Flux distribution histograms of RDG and NLSY (The red line in the figure represents Gaussian fitting，and the green line represents log-normal fitting)

流量分布的正态性有加法模型和乘法模型。在加法模型中，观察到的流量是几个区域贡献的总和，根据中心极限定理(Central Limit Theorems, CLT)可知，此时流量的总和遵从正态分布。在乘法模型中，流量自然产生对数正态性分布。令φ是大量各向同性区域流量A的乘积，即

(1)

(2)

(3)

那么φ的对数是A的对数和，根据中心极限定理，对数logφ遵循正态分布，即φ遵循对数正态分布[24-25]。

2005年，文[10]提出均方根和流量的关系可以解释为流量对数正态分布的结果。假设φ是随机变量x的函数，f(x)=φ。对于对数正态分布来说f为指数函数，x为正态分布，x在x0附近波动，δx在f(x0)附近波动，δφ在f(x0)附近通量的方差为

(4)

当流量与f(x0)成正比时，线性流量均方根关系等价于

(5)

该式是指数函数的定义之一。当且仅当流量是基础变量的指数时，平均流量与均方根成正比，例如流量的对数正态分布。因此流量分布的对数正态性意味着均方根-流量的线性关系。

3 均方根-流量关系

均方根-流量在活动星系核和X射线双星中普遍存在。在X射线双星中，它可以在较短的时间尺度内进行具有高度意义的探测[26]。NLSY1 Ark 564，NGC 4051和Seyfert 1 AGNs MCG-6-30-15等活动星系核的X射线光变曲线的最新研究也存在均方根-流量关系[27-29]。2005年，文[10]提出均方根和流量的关系可以解释为流量的对数正态分布的结果。2012年，文[24]提出了 “mini-jets in jet”，这种模型认为正态分布和对数正态分布都可以解释为更一般的偏态分布，如帕累托分布(Pareto distribution)。在这种情况下，已发现由此产生的通量分布也具有均方根-流量关系[24，30]。

如图2及图3，7个射电星系以及6个窄线型赛弗特星系1分别以10个数据点为一组及1年时间间隔内数据为一组的均方根-流量拟合图都有不同程度的线性关系。如表2，我们分别对射电星系和窄线型赛弗特星系1拟合这两种不同分组的均方根-流量关系并且计算皮尔森相关系数。皮尔森相关系数衡量均方根和流量的相关密切程度。当相关系数的绝对值越大且越接近1.0时，表明均方根和流量相关性越强，相关系数为0.8～1.0表明两者的相关性极强。两种不同分组情况都支持均方根-流量的线性关系。在两种分组情况下，射电星系和窄线型赛弗特星系1的皮尔森相关系数都大于0.8，他们的均方根和流量之间都有强线性关系。射电星系与窄线型赛弗特星系1的斜率都大于0，且射电星系的均方根-流量的斜率稍微比窄线型赛弗特星系1大。

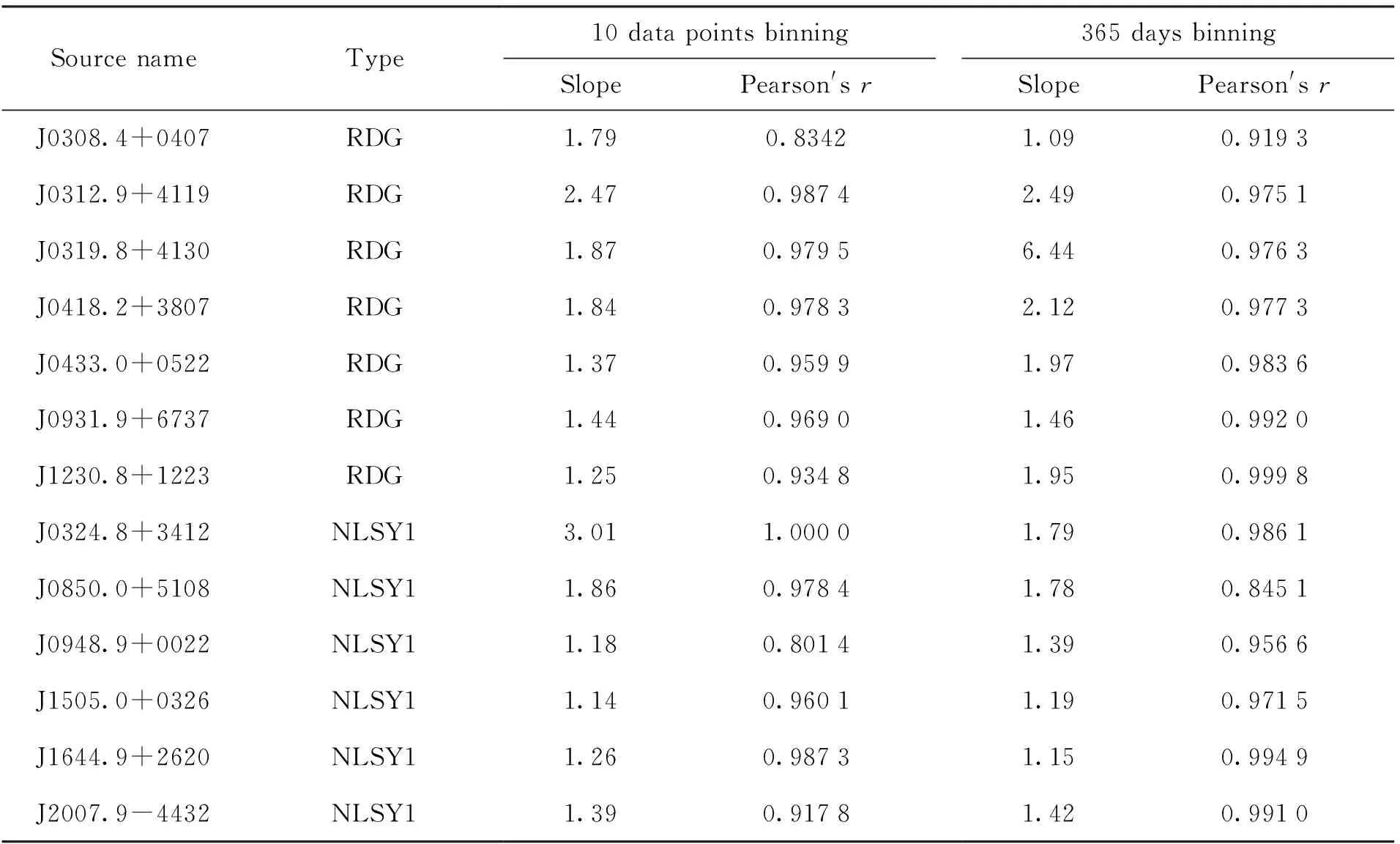
表2 10个数据点为一组和1年时间间隔内数据为一组的射电星系和窄线型赛弗特星系1的斜率和皮尔森系数Table 2 Slopes and Pearson coefficients for RDG and NLSY1 with 10 data points bin and one-year (365 days)bin

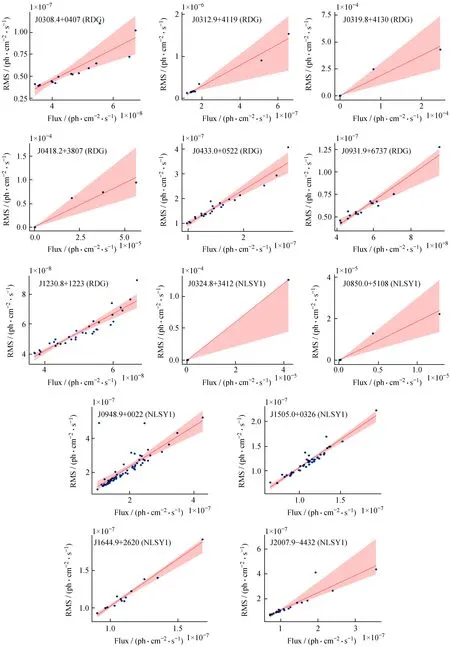
图2 射电星系和窄线型赛弗特星系1取10 个数据点为一组的均方根和流量线性拟合Fig.2 Linear fitting of RMS-Flux correlation by taking 10 data points bin from RDG and NLSY1

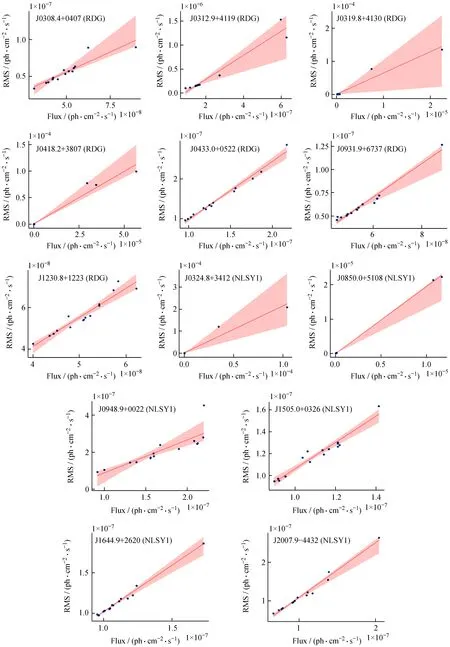
图3 射电星系和窄线型赛弗特星系1以1年时间间隔数据(365 days)为一组的均方根和流量线性拟合Fig.3 Linear fitting of RMS-Flux correlation by taking one-year bin (365 days)from RDG and NLSY1

4 结果和讨论

类星体的长期通量分布对研究光变起源和性质有重要意义。γ射线流量的概率密度函数(Probability Density Function, PDF)可以为高能发射过程提供重要线索。在γ 射线波段的分析下，流量直方图和均方根-流量描述了7个射电星系和6个窄线型赛弗特星系1源的特征。这些源的直方图除了显示出一个突出的峰之外，在流量变化方面都具有数量级的典型宽度，以及一个延伸的高流量尾部。因此，我们对时间跨度为14年的流量分布直方图进行高斯和对数正态拟合。从结果来看，大部分源的对数正态拟合比高斯拟合更好地描述了直方图。除了研究流量的分布特性外，我们还对这些源进行两种不同情况分组的均方根-流量拟合，在95%的置信度条件下提供了线性拟合图及皮尔森相关系数，由此可见流量与均方根之间呈现正向强线性相关性。

X射线和γ射线波段流量的对数正态通量分布及均方根-流量关系在X射线双星和活动星系核中已经发现[30-33]。流量呈对数正态分布及强线性均方根-流量关系的原因也已经在很多文章中解释[32-35]。 射电星系和窄线型赛弗特星系1的流量分布呈现对数正态暗示着此两类活动星系核中的磁盘-喷流连接。另外，我们可以将正态分布和对数正态分布解释为更一般的偏态分布类别的特殊情况，例如具有不同程度的偏态的帕累托分布。在相对论喷流的背景下，流量分布的对数正态性可能是坡印亭流量占主导地位的喷流具有在发射区域内各向同性分布的小型喷流。在这种 “mini-jets in jet” 的模型产生的通量分布保持均方根-流量关系[24]。

我们选择在 “mini-jets in jet” 模型下讨论对数正态分布以及均方根-流量线性关系。在该模型中，相同、独立且随机定向的小喷流遵循帕累托分布。在这种模型下，流量分布可能符合高斯分布也可能符合对数正态分布，这两种分布都可以呈现本文中的线性均方根-流量关系。流量的对数正态分布暗示着均方根-流量关系，我们分析在两种分组情况下的均方根-流量均有强相关性且其斜率整体大于0，由此可以初步推断射电星系和窄线型赛弗特星系1的均方根关系的强相关性属于内在属性，可能是类星体光变性和类似时间序列的一般性质。这种性质是否具有一般性还需要更多的数据支持。所有可能因素，例如可变磁场和高能粒子的密度、粒子加速作用下的光子密度和扩散过程，以一种复杂的方式耦合，从而导致流量的对数正态分布[23]。

5 总 结

我们通过4FGL-DR3里射电星系及窄线型赛弗特星系1的直方图流量分布及均方根流量分布探究了γ射线波段的光变特性。结果表明，一般情况下，这两种类型的流量分布直方图与高斯分布相比更加服从对数正态分布。但是无论流量的直方图更加趋向于何种分布，在我们分析的源中，均方根-流量都呈现强线性相关性。上述特征与磁重联驱动的 “mini-jets in jet” 的预计统测特征大体一致，在这个模型中的帕累托分布表明，流量分布既可能服从高斯分布又可能服从对数正态分布，均方根-流量存在线性关系。