基于Mathews 和FLAC3D 的采场结构参数优化研究
李 翠,张良兵,陈 涛,罗少琛
(攀钢集团矿业有限公司设计研究院,四川 攀枝花 617063)
0 引言
攀西某地下矿山开采采用无底柱分段崩落法[1],但在实际开采过程中存在环保压力大和矿石损失、贫化率大等问题[2-3],为尽可能回采矿石资源和满足国家环保政策要求,企业提出采用分段凿岩阶段空场嗣后充填法进行地下开采。
采场结构参数是影响矿山安全生产、采场稳定性、矿石损失率和贫化率等的重要因素,其确定对地下开采至关重要。目前,常用经验类比法、Mathew 稳定图表法[4-6]和FLAC3D数值模拟法[7-13]优化空场嗣后充填法的采场结构参数。经验类比法简单实用,但凭借工程经验和相关手册选取,不够严谨;Mathew 稳定图表法主要用于估算采场顶板的暴露面积和充填体侧帮的暴露面积;FLAC3D数值模拟法应用范围广泛,能模拟计算三维的土、岩体及其它材料受力状态下的各种力学行为,常用来优化矿房跨度、矿房长度和阶段高度等采场结构参数,但对讨论充填体侧帮暴露面积等问题时难以奏效。
因此,笔者以攀西某地下矿山采用分段凿岩阶段空场嗣后充填为例,应用Mathews 稳定图法和经验类比法估算采场暴露面积,并基于FLAC3D数值模拟优化采场结构参数,最终推荐符合矿山实际的采场结构参数,为矿山的开采设计提供理论依据。
1 工程概况
攀西某地下矿山矿区构造比较复杂,矿区内有五个矿带,矿带内矿体呈层状、似层状产出,层状矿体中夹石及低品位矿石居多。矿体、围岩、夹层或夹石成分多为辉长岩。辉长岩体呈北东~南西向展布,长约20 km、宽约2 km,面积约40 km2。岩体呈单斜层产出,倾向北西,倾角一般50°~60°。原设计采用无底柱分段崩落采矿法进行开采,设计主要参数为进路间距18 m、分段高度20 m。
2 采场暴露面积估算
攀西某地下矿山矿区与采矿工程稳定性关系较为密切的矿岩为辉长岩,矿体与围岩、夹石都是辉长岩,考虑到攀西某地下矿实际情况,本研究重点采用Mathews 稳定图法确定采场允许暴露面积值,结合经验类比法推荐合理值。
2.1 基于Mathews 稳定图法估算
Mathews 稳定图法是加拿大Mathews 所创,基于Q系统分级,通过利用若干稳定图确定形状因子,进而确定采场暴露面积值。Mathews 稳定图法的设计过程以稳定数因子N和形状因子(或水力半径)S计算为基础,将两个因子绘制在划分为预测稳定区、潜在不稳定区和崩落区的图上。稳定数因子N 代表岩体在给定应力条件下维持稳定的能力,形状因子或水力半径S则反映采空区尺寸和形状。
攀西某地下矿山Q系统分级评分结果见表1,岩体稳定数N 的计算公式如式(1)所示,计算结果见表2。

表1 Q 值系统评分结果Table 1 Q-value system rating results
式中,Q′为修正的Q系统分级值;A为岩石强度因子,为在评价的采空面边界上岩石单轴抗压强度 σc与诱生的压应力 σ1之比;B为节理方向调整参数;C为重力调整因子。
待分析帮壁或采空面的形状因子S的计算公式如式(2)所示:
结合攀西某地下矿山现场实际,参照图1,按辉长岩的稳固性确定矿房宽度为15 m,计算各类矿岩的暴露面积,计算结果见表3。其中,对于采场顶板,当计算长度值超过宽度的4 倍时,按长宽比为4∶1重新进行计算。
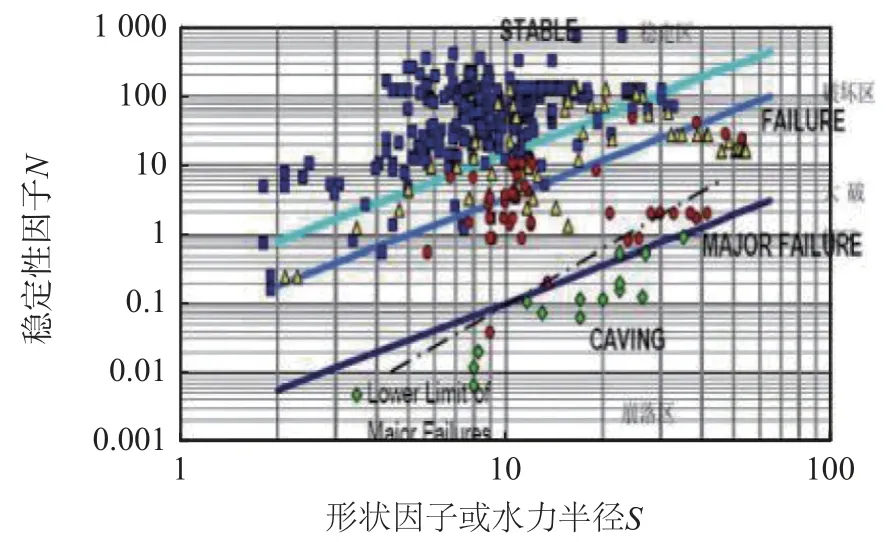
图1 Trueman 扩展的Mathews 稳定图(2000)[14]Fig.1 Trueman extended Mathews stability graph (2000)
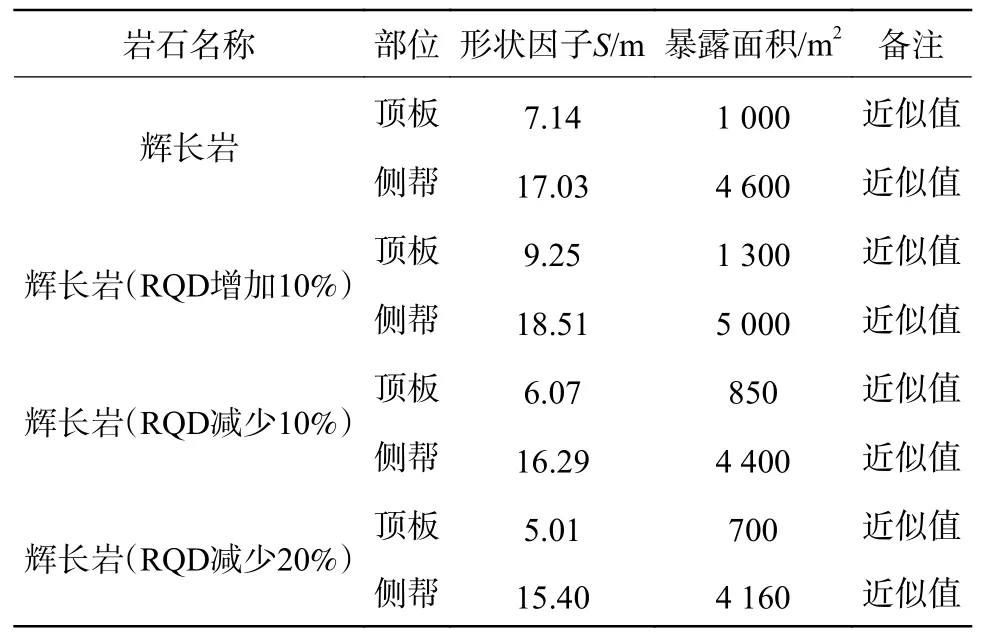
表3 Mathews 稳定图法估算的采场暴露面积Table 3 Estimation of exposed area of mining stope using Mathews stability map method
由表3 可知,矿房宽度相同时,随辉长岩的RQD 值减小,采场形状因子和顶板、侧帮暴露面积总体呈下降趋势,故岩体的力学强度对采场暴露面积影响较大。经Mathews 稳定图法估算,攀西某地下矿山顶板允许暴露面积范围为700~1 300 m2,侧帮允许暴露面积取值范围为4 160~5 000 m2。
2.2 基于经验类比法推荐合理值
参照国内外空场回采嗣后充填法矿山[15],采场顶板暴露面积一般都控制在1 500 m2之内。通常顶板暴露面积超过1 500 m2时,采场岩体的稳定性较好;《有色金属矿山生产技术规程》中阐明,仅极稳固的岩体回采时允许的暴露面积才可大于1 000 m2,这一看法较为保守。从矿石自身强度来看,攀西某地下矿山的铁矿石单轴抗压强度平均为100 MPa,但其节理裂隙略为发育,且仅在节理裂隙不发育处采场顶板暴露面积才可达到1 600 m2。故推荐攀西某地下矿山合理的采场顶板暴露面积为800~1 200 m2。
矿体侧帮暴露面积一般不超过8 000 m2,一般控制在6 000 m2之内[15]。湖南郴州柿竹园铅锌矿[16]的空场高度达90 m,长67 m,矿石单轴抗压强度平均为150 MPa,侧帮暴露面积为6 030 m2,空区的稳定性较好,开采10 余年仅小部分跨塌。当侧帮暴露面积达到8 000 m2时,岩体的稳定性较好。李楼-吴集铁矿[17]采用两步骤嗣后充填采矿法,阶段高度100 m,矿房和矿柱宽度均为20 m,侧向暴露面积达到4 000~6 000 m2,仅在节理裂隙不发育处,矿体侧帮暴露面积才可达到8 000 m2。故推荐攀西某地下矿山合理的采场侧帮暴露面积为4 000~5 000 m2。
综上所述,根据攀西某地下矿山岩体的节理裂隙发育程度,推荐不同岩性或充填体的暴露面积值,详见表4。
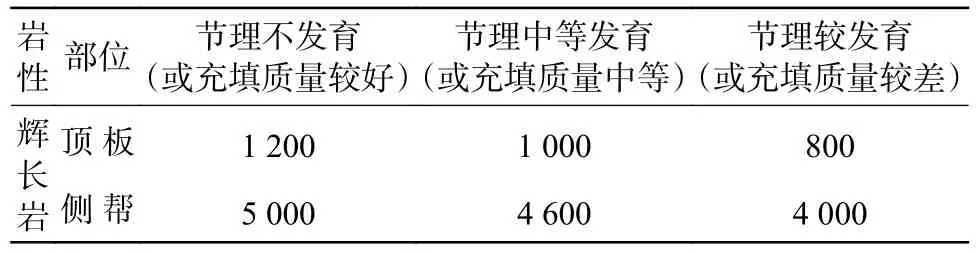
表4 不同节理裂隙程度的辉长岩暴露面积值Table 4 Exposed area values of gabbro with different joint fissure degrees
3 基于FLAC3D 数值模拟分析
FLAC3D(Fast Lagrangian Analysis of Contimua in Three-Dimensions)是由美国Itasac consulting Group Inc 开发的三维显式有限差分计算程序,能模拟计算三维的土、岩体及其它材料受力状态下的各种力学行为。
本研究结合攀西某地下矿山现场实际,选取矿房宽度15 m,重点采用FLAC3D数值模拟分析矿房长度和阶段高度,推荐合理值。
3.1 基于FLAC3D 数值模拟分析
3.1.1 岩体力学参数选取
攀西某地下矿山与采矿工程稳定性关系较为密切的矿岩为辉长岩,相关岩体力学参数见表5。

表5 数值模拟计算所用的材料物理力学参数Table 5 Physical and mechanical parameters of materials used in numerical simulation
3.1.2 FLAC3D数值模型建立
为提高采场生产能力,采用大采场开采。国内矿山的阶段高度通常在50 m 左右,国外矿山的阶段高度有的超过了200 m。基于国内矿山实际情况,本研究遵循Mohr-Coulomb 屈服准则、采用FLAC3D软件建立模型,分别对矿房宽度15 m,阶段高度60、70 m 和80 m,采场长度40、60 m 和80 m 的矿房进行数值模拟分析。计算模型如图2 所示,计算方案见表6。
图2 采场计算模型Fig.2 Stope calculation model diagram
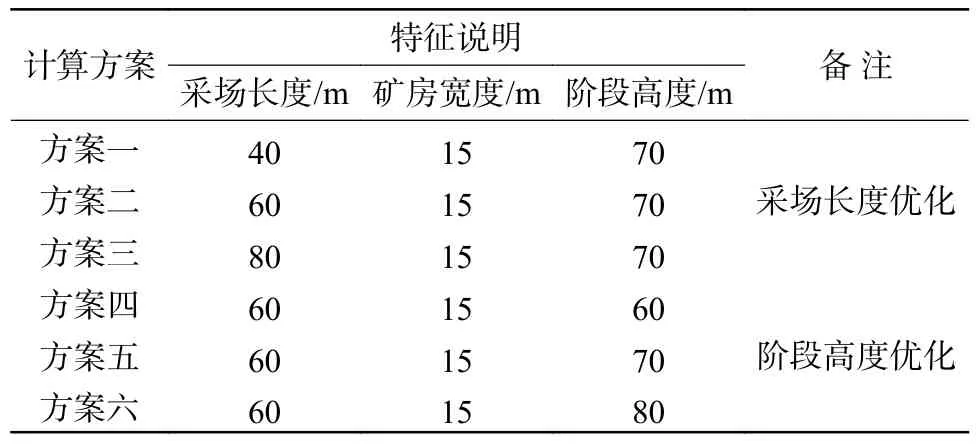
表6 矿房及矿柱合理参数研究计算方案Table 6 Research and calculation scheme of reasonable parameters of room and pillar
3.2 FLAC3D 数值模拟结果分析
3.2.1 采场长度模拟结果分析
空场状态下,应力极值常位于采场周边。采场顶板、两帮及上下盘容易产生拉应力,最大压应力和最大剪应力通常位于2 个或3 个面的交叉处。
采场长度优化方案见表6 中方案一~方案三,矿房宽度15 m、阶段高度70 m,采场长度分别为40、60 m 和80 m,采场长度优化模拟计算见表7,对应云图如图3、4 所示。
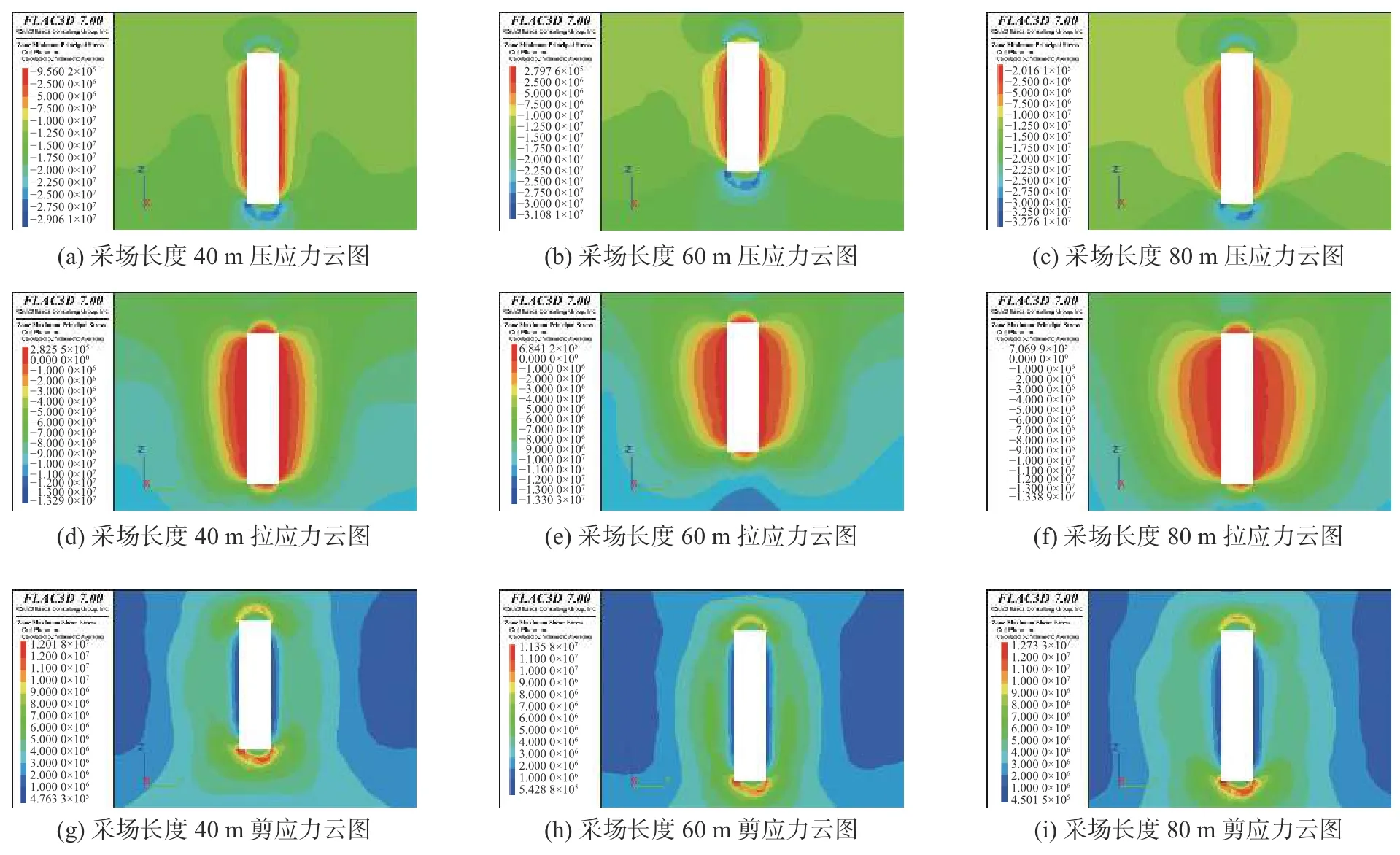
图3 方案一~方案三压应力、拉应力和剪应力云图Fig.3 Cloud charts of compressive stress,tensile stress and shear stress for scheme I to scheme III

表7 采场长度优化模拟计算结果Table 7 Simulation calculation results of stope length optimization
由表7 可知,随采场长度变化,采场顶板的压应力和剪应力均大于采场两帮和上下盘,说明压应力和剪应力集中于顶板处,需加强顶板管理。其中因采场顶板的暴露面积大于两帮,因此最大拉应力集中于采场两帮矿柱中,且随采场长度加大而逐渐增长,增长率分别为54.8%和12.7%。采场长度小于80 m 时,采场周围的最大拉应力值小于0.71 MPa,小于铁矿体的抗拉强度(0.81 MPa)。故通过拉应力不能准确得出攀西某地下矿山的采场长度。
由图3 可知,随采场长度加大,采场周围应力峰值逐渐增大,采场稳定性将受到破坏。尽管采场顶板、两帮及上下盘围岩中的拉应力值迅速增大,但仍未超出矿体的极限抗拉强度和极限抗压强度,因此为准确得出合理采场长度,还需从采场周围最大位移和塑性区范围加以确定。采场开挖结束后塑性区分布情况如图4 所示,图中红色为采场围岩已经发生塑性剪切和张拉变形区域,绿色为采场围岩已经发生塑性剪切变形区域,粉色为采场围岩正在发生塑性剪切变形和已经发生塑性剪切变形区域。
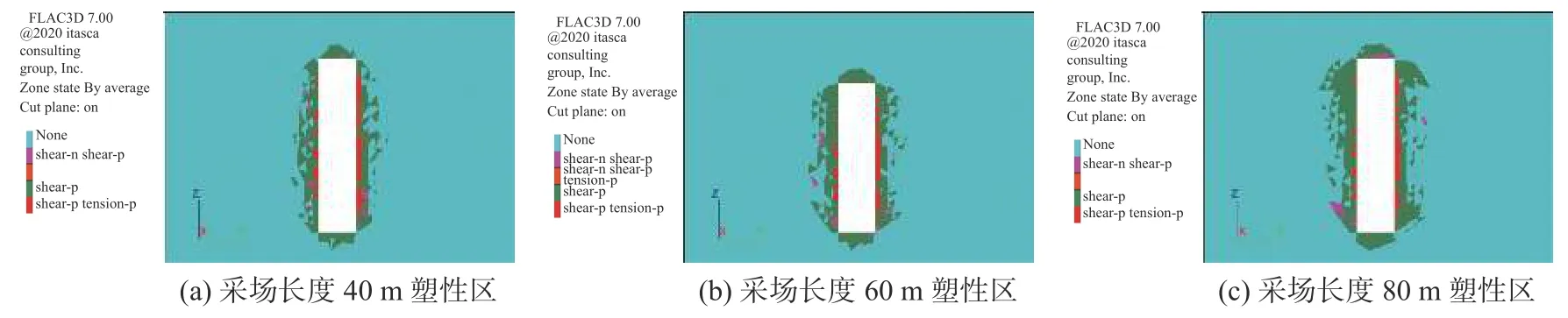
图4 方案一~方案三塑性区图Fig.4 Plastic zone maps for scheme I to scheme III
另外,由表7 可知,采场顶板和两帮的最大位移随采场长度加大而增大。其中,采场顶板受采场长度的影响更大,当采场长度由40 m 增大至60 m 时,采场顶板最大位移增长率为25%;而当采场长度由60 m 增大至80 m 时,采场顶板最大位移增长率为180%。故采场长度不宜大于60 m。
由图4 可知,采场围岩张拉变形主要集中在采场两帮,侧向证明采场两帮拉应力比较集中。采场长度为60 m 时,采场顶板没有发生正在进行的剪切变形,直到采场长度大于60 m 后,采场顶板开始发生正在进行的剪切变形,导致采场内顶板稳定性较差。故采场长度为60 m 最为适宜。
3.2.2 阶段高度模拟结果分析
阶段高度优化方案见表6 中方案四~方案六,采场长度60 m、矿房宽度15 m,阶段高度分别为60、70 m 和80 m,采场阶段高度优化模拟计算结果见表8,对应云图如图5 所示。
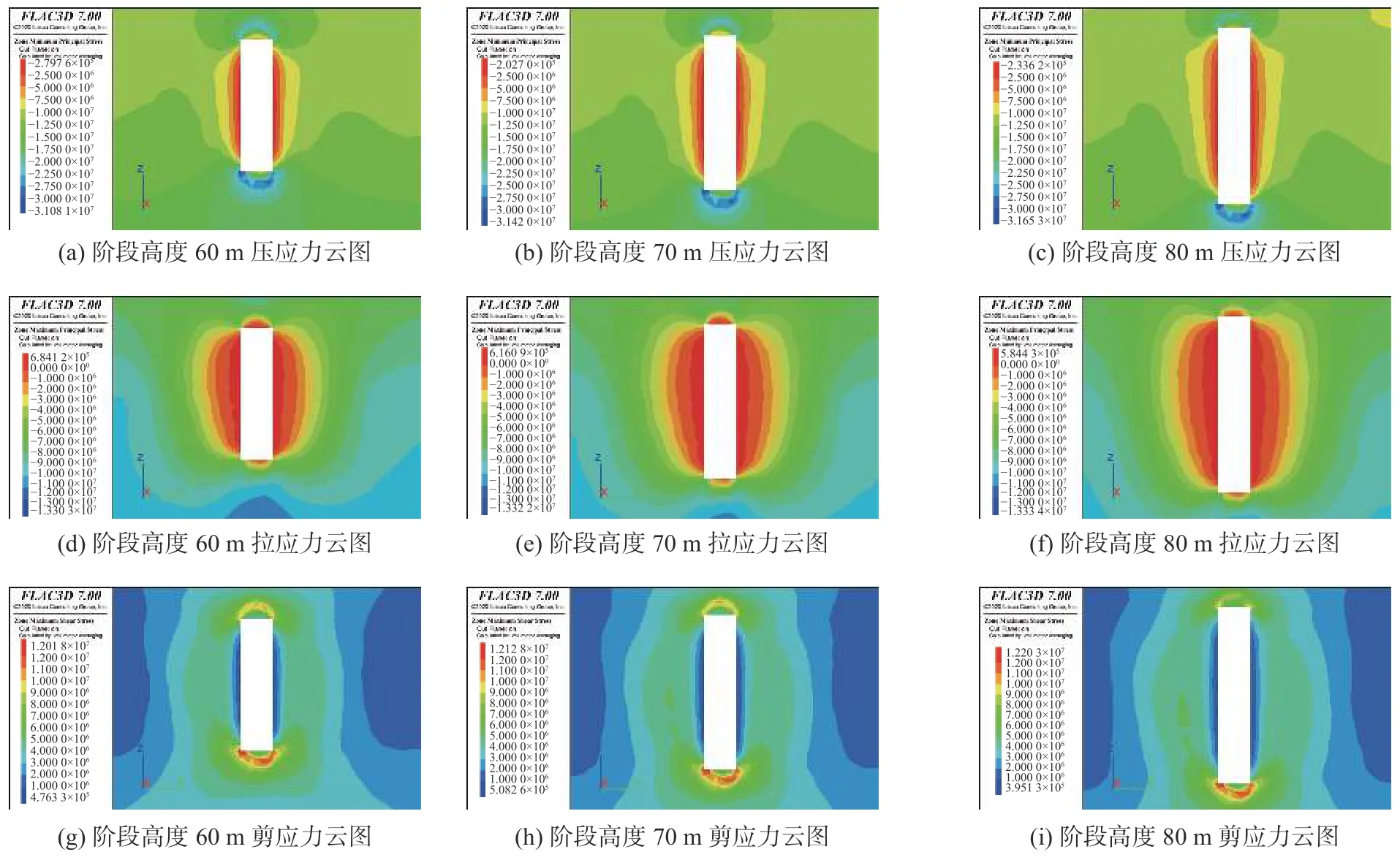
图5 方案四~方案六压应力、拉应力和剪应力云图Fig.5 Cloud charts of compressive stress,tensile stress and shear stress for scheme Ⅳ to scheme Ⅵ

表8 采场阶段高度优化模拟计算结果Table 8 Optimization simulation results of stope stage height
由表8 可知,随阶段高度增大,采场周围的最大拉应力、最大压应力和最大剪应力均呈增长趋势。其中,各阶段高度采场顶板的压应力和剪应力均大于采场两帮和上下盘,说明压应力和剪应力集中于顶板处,需加强顶板管理。其中因采场顶板的暴露面积大于两帮,因此最大拉应力集中于采场两帮矿柱中,并随阶段高度增加而逐渐增大,增长率分别为6.8%和9.6%。阶段高度小于80 m 时,采场周围的最大拉应力值小于0.68 MPa,小于铁矿体的抗拉强度(0.81 MPa)。故通过拉应力不能准确得出攀西某地下矿山的阶段高度。
由图5 可知,随阶段高度增大,采场周围应力峰值逐渐增大,采场稳定性将受到破坏。尽管采场顶板、两帮及上下盘围岩中的拉应力值迅速增大,但仍未超出矿体的极限抗拉强度和极限抗压强度,因此为准确得出合理阶段高度,还需从采场周围最大位移和塑性区范围加以确定,如图6 所示。
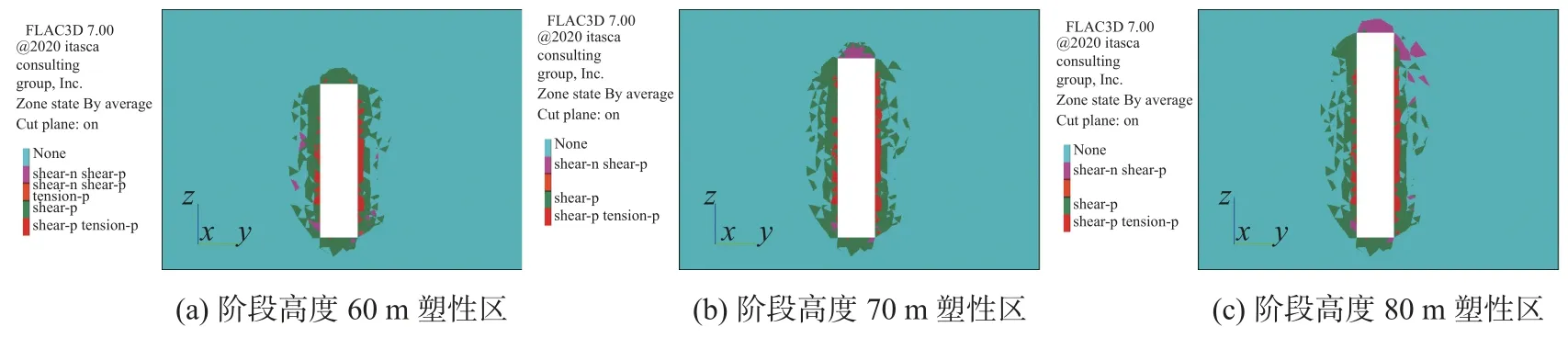
图6 方案四~方案六塑性区图Fig.6 Plastic zone maps for scheme Ⅳ to scheme Ⅵ
另外,由表8 可知,采场顶板和两帮的最大位移随阶段高度增加而增大。其中,采场顶板受阶段高度的影响更大,当阶段高度由60 m 增加至70 m 时,采场顶板最大位移增长率为66.6%;而当阶段高度由70 m 增加至80 m 时,采场顶板最大位移增长率为220%。故阶段高度不宜大于70 m。
由图6 可知,采场围岩张拉变形主要集中在采场两帮,侧向证明采场两帮拉应力比较集中。阶段高度为60 m 时,采场顶板没有发生正在进行的剪切变形,直到阶段高度大于60 m 后,采场顶板开始发生正在进行的剪切变形,导致采场内顶板稳定性较差。故阶段高度为60 m 最为适宜。
综上所述,为更好与攀西某地下矿山现有开拓系统良好衔接,推荐采场长度为60 m、阶段高度为60 m。
4 结论
1)采用Mathews 稳定图法和经验类比法对攀西某地下矿山暴露面积值进行估算,最终推荐采场顶板允许暴露面积为800~1 200 m2,矿体侧帮允许暴露面积为4 000~5 000 m2。
2)采用FLAC3D对攀西某地下矿山结构参数进行数值模拟分析,发现随采场长度和阶段高度增大,采场周围的最大拉应力、最大压应力和最大剪应力都呈增加趋势。结合矿山现有开拓系统,攀西某地下矿山阶段高度为60 m,采场长度为60 m 最为适宜。

