面向大区域碳卫星数据的分布式Kriging插值算法优化
周小华,王学志,周园春,孟 珍
(1.中国科学院计算机网络信息中心,北京 100083;2.中国科学院大学,北京 100049)
1 引言
因碳排放增加导致的全球气候变暖问题日益突出,正对人类现在及未来的社会经济活动产生深远影响。2016年全世界178个缔约方共同签署了《巴黎协定》,呼吁国际社会共同努力将全球温度上升幅度控制在2 ℃以内。我国也于2020年提出了2030年碳达峰与2060年碳中和的目标[1]。通过碳卫星检测碳排放的方式具有连续、稳定、大范围、不受地形限制等优点,为全球各个区域在不同时期的碳排放量化评估提供了重要的技术手段。
近年来,中国、美国、加拿大及日本等国家相继发射多颗碳卫星,目前仍在轨运行的有OCO-2(美国,2014年)、TANSAT(中国,2016年)、GOSAT-2(日本,2018年)、OCO-3(美国,2018年)、DQ-1(中国,2022年)等[2]。大部分碳卫星基于自身运行轨道以线性散点的形式采集并存储探测数据,在进行大区域CO2浓度分布量化评估时,需要通过空间插值来弥补缺失区域值。
在上述卫星中,OCO-3卫星时空覆盖范围更广,数据经过严格的校准处理,具有更高的测碳精度,且所有数据均可公开访问,是目前进行全球碳排放检测与研究的重要数据源[3-5]。因此,本文以OCO-3卫星数据为例进行面向碳卫星数据的Kriging插值算法的优化研究。
2 相关工作
空间插值是指利用周围已知样本点基于拟合函数,对未知点的值进行预测的方法。常用的空间插值方法从原理上可分为2大类:确定性方法和地学统计方法。确定性方法基于已知点的相似度或曲面的平滑程度来预测未知点的值,如反距离权重法、径向基函数插值法等;地学统计方法则通过量化样本数据点之间的空间自相关性,构造空间结构模型,进而对未知点的值做出预测,如Kriging插值法[6]。
Kriging插值算法可以给出最优线性无偏估计BLUP(Best Linear Unbiased Prediction),在插值时综合考虑了距离及空间自相关性等因素,具有较高的插值精度[7]。Kriging算法根据前提条件与应用场景的不同又可分为普通Kriging算法、泛Kriging算法、协同Kriging算法及析取Kriging算法等。其中普通Kriging算法是ArcGIS推荐使用的默认插值算法,应用最为广泛,为此本文将基于普通Kriging算法对OCO-3数据的大区域尺度插值进行研究。
Kriging插值过程比较复杂:在插值前需要计算所有样本点两两之间的距离与协方差,然后拟合得到半变异函数模型,进而对未知点进行插值预测,其中包含矩阵乘积和矩阵求逆等耗时操作。假设有n个数据点和m个未知点,Kriging插值的整体时间复杂度为O(m·n3),在大区域尺度上直接应用Kriging算法进行空间插值计算量很大[8]。
以OCO-3数据为例,覆盖中国区域的约有150万个数据点,假设已知样本点占一半,即75万个点,仅计算这75万个点中任意两点之间的距离与协方差需要约5 000亿次运算,基于普通配置的单台服务器完成上述运算需要30天左右,耗时难以接受。
目前针对Kriging插值算法的并行加速优化方案主要有2种。一种是在高性能计算环境中改造Kriging算法,利用众核处理器、超高速网络等硬件优势对其进行加速。文献[9,10]在单机多核服务器上采用OpenMP实现了并行Kriging插值;文献[11-13]基于MPI、MKL等技术结合Cholesky分解法、Gauss-Jordan消元法等矩阵优化算法实现了支持多达512核的并行Kriging插值加速;文献[14]解决了空间分布不均匀的待插值数据在多核CPU上的负载均衡问题。近年来,随着GPU核数的不断攀升以及共享显存的持续扩大,GPU的并行计算能力已远超主流CPU的,并在科学计算领域取得了广泛应用。文献[15-17]介绍了基于OpenCL、CUDA等技术在GPU上实现并行Kriging插值的方法;文献[18-20]进一步研究了基于CPU-GPU协同的Kriging并行插值的实现途径与方法。
以上工作均取得了较高的加速比,显著提升了Kriging插值效率,但由于对特殊硬件设备及编程环境的依赖,存在使用成本高、开发编程难等问题,而且普遍缺乏容错机制,水平扩展能力差[21]。
另一种方案是基于目前较成熟的分布式计算框架(如Spark、Hadoop等)在多台机器上实现Kriging插值的并行加速。分布式计算框架采用计算向数据迁移、分布式内存、懒计算等技术提升海量数据的处理效率,同时具有较强的容错能力,可在大规模集群上实现快速可靠的并行计算。文献[22,23]在 Hadoop上实现了分布式Kriging并行插值,与基于CUDA-GPU的方式相比,虽然效率较低,但水平扩展能力强,且具有更好的可靠性和易用性。文献[24]介绍了基于Spark实现分布式Kriging并行插值的技术方案,并就处理时间、CPU内存利用率等与Hadoop进行了对比,其整体效率达到了Hadoop的5倍左右。以上方案本质上均是基于MapReduce架构对数据分块然后进行分布式插值,数据分块一般采用固定空间区域或滑动窗口等方式。固定空间区域会使边界附近的未知点因近邻样本点选择不全而导致插值结果不准。滑动窗口方式虽然可以在一定程度上避免这一问题,但会因不同子数据块空间区域重叠而产生大量的重复计算,影响整体计算效率。
文献[25]将所有待插值数据看作一个整体,优化了Kriging插值过程中的矩阵求逆乘积运算,在Spark上实现了面向大矩阵的分布式Kriging插值。OCO-3数据插值所采用的近邻点一般不会超过50个,对应矩阵规模较小,求逆乘积等速度非常快,没必要进行矩阵运算的分布式加速。
此外,OCO-3原始数据按照国家空间站ISS(International Space Station)航线采集,是一种线性时空数据,在通过Kriging插值生成最终的CO2浓度分布数据时,还需要一些特殊的空间操作,如坐标重投影、并行时空检索、矢量结果栅格化等,而Hadoop、Spark等针对这类空间操作的加速效果并不理想[26]。
本文综合以上问题,提出另一种方案:将过程复杂、计算量大的Kriging插值过程重构为可多步执行的DAG结构的工作流,并基于具体的数据特征对其中的复杂计算环节进行优化;然后将计算任务进一步拆分,细化插值粒度,形成可在分布式环境下并行执行的计算任务,在底层通过一个双层架构的分布式工作流调度引擎对拆分后的插值任务进行并行加速。与其他方案相比,本文方案对硬件环境无特殊要求,插值任务调度执行效率高,且架构灵活易实现,可根据空间区域尺度和待插值数据量动态调整集群规模,具有较强的可扩展性。
3 数据统计特征分析
OCO-3卫星数据中包含多项与CO2相关的指标,最常用的是XCO2,即二氧化碳柱浓度,单位为PPM(Parts Per Million volume),其数据覆盖空间为[-180,-52,180,52],平均采样分辨率约为2.5 km*2.5 km,采集轨道如图1所示。

Figure 1 OCO-3 satellite data collection track图1 OCO-3卫星数据采集轨道
基于Kriging算法对OCO-3数据进行插值包含2个步骤:(1)分析OCO-3数据的统计特征并对其空间相关关系进行建模;(2)基于构建的空间模型进行插值。针对未知点p的插值公式如式(1)所示:
(1)
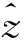
λ应当是一组使得p点预估值与真实值误差最小的权重系数,据此构造目标函数f(λ)如式(2)所示:
(2)
将式(1)代入式(2),结合普通Kriging插值的应用条件,使用拉格朗日乘数法可得λ的求解公式[27],如式(3)所示。
(3)
其中,rij是基于距离求得的半变异函数值;样本点个数n由样本点密度与半变异函数模型决定,通常控制在20~100内,太少会使部分相关性强的点不能参与插值,太多会让过多无关点参与插值,二者都会导致插值结果不准。
半变异函数模型基于近邻样本点的距离与协方差通过最小二乘法拟合得到。常见的半变异函数模型有球形模型、圆形模型、指数模型、高斯模型及线性模型等。本文随机选取100个样本点,并分别计算与其相邻的500个数据点的距离与协方差,然后以5 km为区间计算协方差的平均值,得到各个样本点对线性模型的拟合度分布,如图2所示。
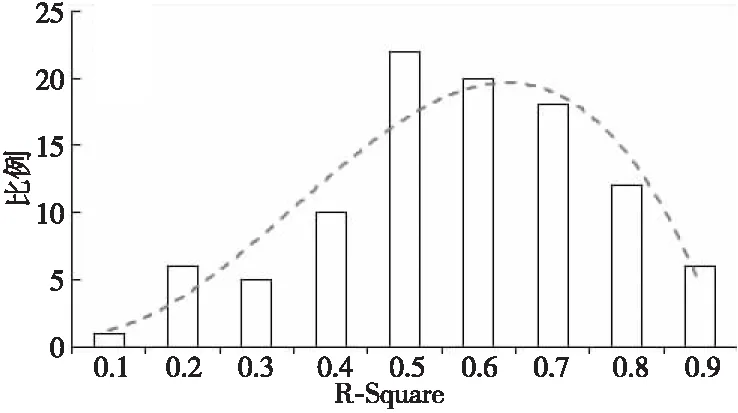
Figure 2 Distribution of linear model fitting图2 线性模型的拟合度分布
由图2可知,拟合度超过0.5的数据点占比接近80%,因此本文选取线性模型作为OCO-3数据的插值函数模型。
4 整体概述
基于以上分析,本文设计并实现如图3所示的分布式Kriging插值加速框架。该框架以用户指定的时空范围及目标分辨率为输入,输出结果为栅格化的XCO2浓度分布影像,插值过程分为2个阶段:Kriging插值工作流构建和工作流任务的分布式并行加速。在工作流构建阶段,将串行的Kriging插值过程细化拆分为多个相对独立的任务模块,并根据其输入输出的依赖关系确定不同任务的执行时序;然后根据数据特征与计算模式将每个独立的任务模块进一步拆分为可并行执行的子任务;最后由底层面向DAG工作流的分布式调度引擎负责加速执行。

Figure 3 Distributed Kriging interpolation framework for OCO-3 data图3 面向OCO-3数据的分布式Kriging插值框架
底层的分布式调度引擎基于管理与计算分离的双层架构实现。第1层主要负责控制整个工作流任务按序向前推进。第2层负责工作流中具体子任务在分布式环境中的调度执行。
基于上述结构划分,下文将首先介绍Kriging插值工作流的构建细节及其中关键步骤的优化方法;然后介绍如何将Kriging插值工作流转换为可在分布式环境中并行执行的任务以及面向该任务的分布式调度引擎的设计与实现。
5 插值工作流的构建与优化
结合OCO-3卫星数据特征构建Kriging插值工作流,如图4所示。

Figure 4 Workflow of Kriging interpolation for large region图4 面向大区域尺度的Kriging插值工作流
整个工作流包含3个主要模块:(1) 数据解析处理:通过时空检索得到指定时空范围内的原始线性排列的散点数据,将其网格化,然后计算并缓存所有数据网格之间的距离与协方差;(2) 网格遍历插值:逐个遍历所有未知网格,基于其近邻网格之间的距离与协方差拟合半变异函数模型,以此对未知网格进行插值;(3) 插值结果汇总:整合所有数据网格与插值网格,结合空间位置信息,将其栅格化为XCO2浓度分布影像。
在上述工作流中,时空检索、近邻点筛选以及全局距离协方差计算是比较耗时的3个环节,为此本文基于网格剖分、数据分链等方式对其进行了有针对性的优化,使整体插值效率得到显著提升,具体优化细节如下文所述。
5.1 分布式并行时空检索
直接基于大尺度不规则的空间区域进行检索十分耗时,为此,本文在对原始OCO-3数据点构建空间索引(RTree)的基础上,进一步将空间检索范围由中心点进行递归网格化拆分,将单个不规则大区域的空间相交查询转换为多个矩形网格的并行相交查询。算法伪代码如算法1所示。
算法1基于网格的并行时空检索算法
输入:最小网格G(w,h),空间查询范围R。
输出:与R相交的OCO-3数据点集合RST。
//计算R的外包矩形
x0,x1=min(R.coords[:,0]),max(R.coords[:,0]);
y0,y1=min(R.coords[:,1]),max(R.coords[:,1]);
//调整外包矩形使其为G的整数倍
a,b,c,d=align(x0,y0,x1,y1);
grids=[[a,b,c,d]];
G1=[];//位于R内部的网格
G2=[];//位于R边界的网格
whilenotgrids.empty():
g=grids.pop();
ifR.contains(g)://g位于R内部
G1.append(g);
elseifR.intersects(g)://g位于R边界
ifg.area()≤Smin:
G2.append(g);
else:
//以G为单位将g近似等分为4个子网格
subgrids=quad_split(g,G);
forsginsubgrids:
grids.append(sg);
endfor
endif
endif
endif
endwhile
rst1=parallel(query_by_extent,G1);
rst2=parallel(query_by_intersect,G2);
RST=merge(rst1,rst2);
returnRST;
算法1中的query_by_extent通过直接比较数值大小的方式获得目标数据,query_by_intersect则先通过数值比较的方式快速缩小搜索空间,然后通过精确空间相交判断获得目标数据。parallel是将以上2个函数分布到不同服务器节点并行执行的方法。
图5是基于以上算法对新疆省边界进行网格化拆分后的效果。
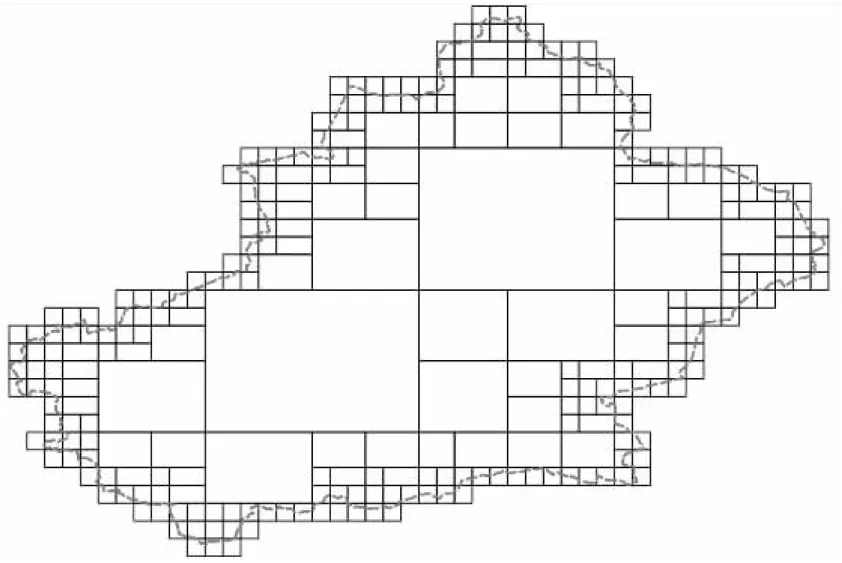
Figure 5 Illustration of grid dividing of spatial range图5 空间范围网格拆分示意图
对空间区域网格化后,所有网格都可独立地由不同节点上的计算进程进行查询。大部分数据可以基于内部少量大网格通过query_by_extent快速查询得到,剩余数据则基于边界小网格通过query_by_intersect查询得到,小网格虽然数量多,但网格面积大大缩小,查询速度也有显著提升。
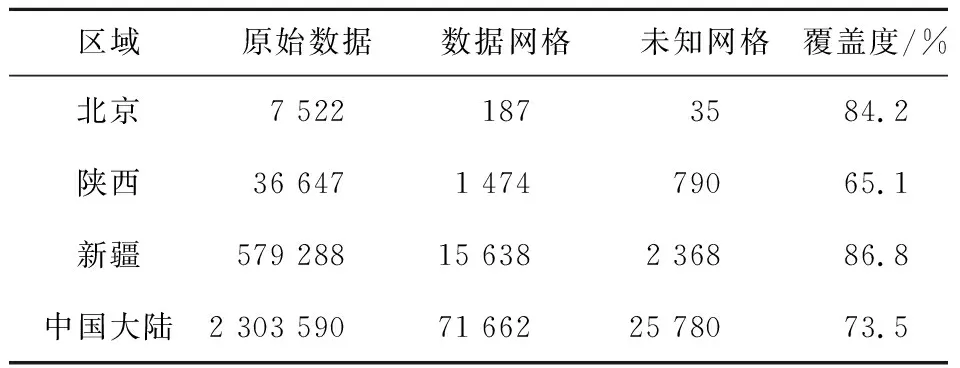
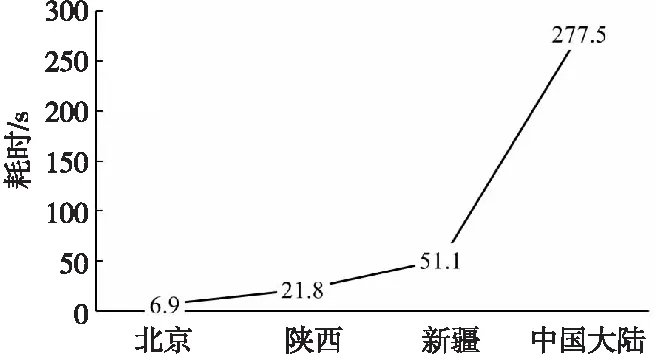
采用上述方法分别检索中国大陆、新疆、陕西及北京等4个不同大小区域的OCO-3数据,与直接基于单个大区域的查询方式的耗时对比如表1所示。

Table 1 Comparison of spatial retrieval time in different regions表1 不同区域尺度的空间检索耗时对比 s
由表1可知,上述基于网格拆分的并行时空检索优化方法可以显著提升检索效率,且空间范围越大,速度优势越明显。
检索到原始数据后按照目标分辨率对其进行网格化处理:取处于同一个网格的所有样本点的均值作为该网格的XCO2值,网格位置用中心点表示,同时对所有网格按照行列进行编号。网格编号规则如式(4)所示:
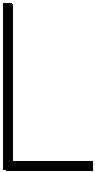
(4)
其中,gm为行编号;gn为列编号;(px,py)为网格的中心点坐标;dt为用户指定的分辨率,即网格边长。
5.2 近邻数据点筛选
KDTree是常用的近邻数据点筛选方法,但其在查询时,每次都要回溯到根节点,且效率会随着样本数据量的增加大幅下降。另一种思路是基于空间填充曲线将待索引空间分为多级网格,并对每个网格赋予一个带有位置信息的编号,进而将二维空间的坐标点映射到一维空间,基于该特性可以快速得到处于同一空间区域的数据点。GeoHash、Google S2等都是基于该思路的空间索引算法,空间填充曲线虽然在一维空间里尽可能地维持了空间本地性,但仍有一定的”跳跃”,即部分编号相邻的网格实际相距较远,直接通过编号前缀获得的候选节点并不全部准确。
考虑到OCO-3样本数据网格化后分布比较均匀,本文设计并实现了更快的近邻搜索算法,如图6所示。

Figure 6 Illustration of neighbor search based on grids图6 网格化近邻搜索示意图
图6中,gx为待插值网格,网格编号为(rx,cy);sr为近邻搜索的最大距离;dt为网格边长;ceil为向上取整函数;floor为向下取整函数。在圆形区域内部及边界的数据网格即为所求近邻数据网格,具体筛选步骤如下:
(1)计算圆形区域的外包矩形范围:Ro= [ox0,oy0,ox1,oy1],计算公式见图6;
(2)计算圆形区域的内接正方形范围:Ri=[ix0,iy0,ix1,iy1],计算公式见图6,该范围内的所有数据网格均为待插值点的近邻数据网格;
(3)逐个遍历介于Ro与Ri之间的数据网格,筛选出所有与gx距离小于sr的网格;
(4)汇总步骤(2)与(3)的结果,即为gx的所有近邻数据网格。
步骤(1)通过外包矩形快速锁定一个较小的候选网格范围。步骤(2)则通过内接矩形直接确定了大部分近邻数据网格。以上2个步骤都是基于简单的公式计算完成,时间复杂度为O(1)。介于Ro与Ri之间的数据网格需要逐个遍历,但数量较小,不会对整体耗时产生明显影响。
5.3 全局距离协方差计算
Kriging插值的核心步骤是计算未知点近邻数据网格两两之间的距离和协方差,进而以此拟合得到用于插值的半变异函数模型。由于相邻未知网格的近邻数据网格重叠度较高,本文采用预先计算并缓存的方式来避免重叠区域的重复计算。此外,考虑到插值只用近邻数据,为此在执行计算时,只采用一定范围内的数据网格,范围大小由目标分辨率与数据分布特征确定。
直接计算所有数据网格两两之间的距离与协方差计算量太大(如图7a所示),耗时无法接受,而且由于交叉太多,难以并行加速。分块计算再合并的方式(如图7b所示)可以实现并行加速,但合并过程比较复杂,且难以应用距离限制计算量。针对以上问题,本文采用如图8所示的分行链式结构对数据进行重新组织,以实现分布式环境下的全局距离与协方差的并行计算。

Figure 7 Two modes of global distance and covariance computation图7 2种全局距离协方差计算模式

Figure 8 Linked structure of data samples图8 样本数据点的链式组织结构
图8中,xn表示数据网格的横坐标,y(n,i)表示数据网格的纵坐标,v(n,i)为XCO2值。距离基于位置(xn,y(n,i))计算,协方差基于v(n,i)计算,采用当前行向右,跨行由中间向两侧的遍历策略进行计算(如图9所示)。算法伪代码如算法2所示。
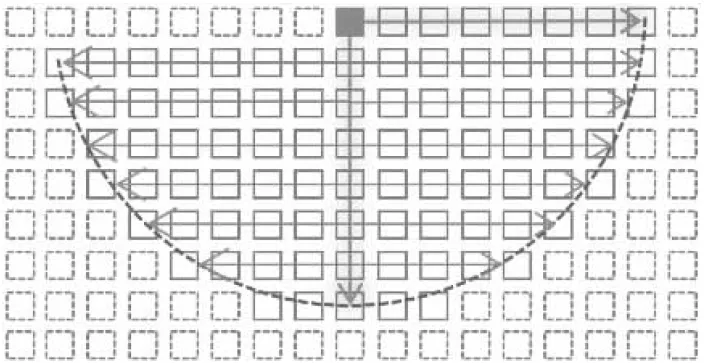
Figure 9 Illustration of distance and covariance computation between neighbor data points图9 相邻数据点距离协方差计算示意图
算法2相邻数据网格距离协方差计算
输入:行列号为(M,N)的数据网格G。
输出:相邻数据网格之间的距离与协方差字典DVS。
forginnext(M,N)://行内向右遍历
//距离、协方差计算
d,v=dist(g,G),cov(g,G);
ifd>MAXDIST:
break;
endif
DVS[(G,g)]=(d,v);
endfor
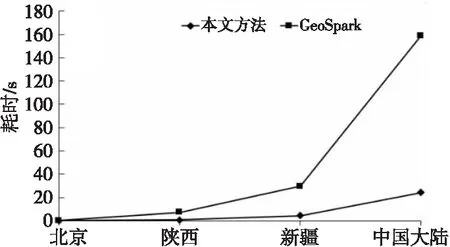
m,n=G.M+1,G.N;//开始逐行向下遍历
whilem forginnext(m,n)://行内向右遍历 d,v=dist(g,G),cov(g,G); ifd>MAXDIST: break; endif DVS[(G,g)]=(d,v); endfor forginpre(m,n)://行内向左遍历 d,v=dist(g,G),cov(g,G); ifd>MAXDIST: break; endif DVS[(G,g)]=(d,v); endfor m+=1; endwhile 其中,MAXDIST为限定相邻网格的距离常量,根据待插值区域的样本点分布设置;DVS的主键为(m0,n0,m1,n1),m,n为数据网格编号,且满足:(m0 本节介绍如何将上述Kriging插值工作流以及优化算法转换为可并行执行的任务模块,并基于不同任务模块之间输入输出的依赖关系确定调度执行的顺序,最后通过一套双层架构的分布式调度引擎实现上述工作流任务的并行加速。 整个工作流分为5个主任务:并行时空检索(T1)、全局距离/协方差计算(T2)、近邻点筛选(T3)、半变异函数拟合并插值(T4)和插值结果栅格化(T5),如图10所示。 Figure 10 Kriging interpolation workflow for distributed environment图10 面向分布式环境的Kriging插值工作流 主任务T1基于时间范围区间划分及空间范围网格化拆分为m个可分布式并行执行的子任务,T1的输出结果为网格化的数据点。主任务T2以T1的输出作为输入,基于分行链式存储结构拆分为n个可分布式并行执行子任务,T2的结果以键值对的形式缓存至Redis内存数据库。主任务T3并行遍历待插值网格,基于5.2节描述的算法获取每个待插值网格的近邻数据网格集合。主任务T4以该近邻数据网格集合以及Redis缓存为输入完成最终的半边异函数拟合与插值,T4的输出结果最终通过主任务T5栅格化为GeoTIFF文件进行存储。主任务的执行时序如图11所示。 Figure 11 Executing sequence of main tasks图11 主任务执行时序 图11中,主任务T2、T3为并行执行,其他主任务均为串行执行,执行到具体某个主任务时,主任务内部的子任务可通过独立调度在分布式环境下并行执行。 基于6.1节所述的工作流任务特点,本文设计并实现如图12所示的双层任务调度框架。第1层为唯一的主调度器,负责主任务的调度管理与时序控制;第2层包含多个分调度器,每个分调度器管理一个或多个计算节点,并具体负责子任务的调度执行,分调度器由主调度器管理,接受并执行主调度器发送过来的调度命令并向其汇报自己的状态。 Figure 12 Framework of double-tier scheduling engine for Kriging interpolation workflow图12 面向Kriging插值工作流的双层任务调度框架 所有主任务按照依赖关系与执行顺序生成一个DAG结构的任务流,其任务节点以任务记录的形式存入主任务队列。任务记录中包含任务标识(id)、前序任务(pre)、后续任务(next)、状态(status)、输入(input)、输出(output)、执行时间(timestamp)等信息。主调度器遍历该任务队列,取出所有满足条件(无前序依赖,且输入条件已满足)的主任务交给分调度器执行,分调度器将主任务对应的子任务通过分布式任务调度引擎将其分发到计算集群上并行执行,并实时监控其运行状态。当前主任务执行结束后,分调度器向主调度器汇报,主调度器据此更新主任务队列中相关的任务状态、前序依赖、输入输出等信息,并继续调度执行符合条件的主任务。 为了实现任务状态快速更新,降低任务调度开销,主调度器与分调度器均采用C++开发实现,并对图10所示的工作流进行拓扑排序形成任务队列,然后将其以键值对的形式存储至有序字典中。其中key为任务标识,value为包含执行该任务的函数名称、参数以及前后任务等信息。 位于底层计算节点的任务执行模块基于Dask实现。Dask打破了Python中GIL(Global Interpreter Lock)的限制,支持多核并行计算与核外计算,且具有不亚于OpenBLAS的矩阵运算效率[28]。 考虑到OCO-3样本点总数量在10亿以内,内存占用不超过50 GB,为了提升数据访问效率,不同计算节点之间的数据共享通过内存数据库Redis实现。 分调度器在执行任务分配时,优先将同一主任务的子任务分配到相同计算节点上,以尽可能降低任务调度管理以及跨节点数据传输等带来的额外开销。计算节点根据自身可用的计算资源设置任务并发数上限,当某个节点负载接近上限时,再由分调度器将待执行任务分配到其他节点。 在上述框架中,主调度器、分调度器与任务执行等各模块相对独立,各个模块之间的任务调度、运行状态、启停命令等消息传递则基于ProtoBuf序列化协议实现,该协议与XML、JSON相比,序列化速度更快、数据体积更小[29]。 根据处理级别与数据内容的不同,OCO-3卫星数据产品分为18种类型。其中,OCO3_L2_Standard V10r为官方推荐数据集,自2019/08/05持续更新至今。截至2021/12/31,已发布了11 380个数据文件,共包含109 315 194数据点,发布的数据产品采用NetCDF-4/HDF5格式存储。为方便后续分析,本文将原始数据中的时间、位置、XCO2等信息以四元组(timestamp,longitude,latitude,xco2)形式进行重新组织,重组后的数据存入关系型数据库PostgreSQL中。 为测试和评估本文所提出的优化算法与计算框架的性能效率,选取了2021年的OCO-3数据进行实验分析,测试环境为6台相同配置(如表2所示)的服务器搭建的集群,服务器之间的网络带宽为1 Gbps。其中,5台服务器用于搭建计算集群,每台服务器的计算任务并发上限数为16,另外1台用作Redis数据库服务器,所有服务器挂载均基于MooseFS搭建的分布式文件系统。 为测试不同区域尺度下的插值效率,本文选取了中国大陆、新疆、陕西、北京等4个边界不规则且大小不同的测试区域,如图13所示。 Figure 13 Interpolation regions of different sizes图13 不同大小的插值区域 基于5.1节介绍的并行时空检索方法得到以上4个区域的原始数据后,按0.1度分辨率对原始样本点数据进行网格化,并取平均值作为该网格的XCO2数值。以上4个区域包含的原始样本数据点个数、数据网格数、未知网格数如表3所示。 Table 3 Size of test data表3 测试数据量 由表3可知,OCO-3数据在不同区域的分布并不均匀,新疆的数据覆盖比例比陕西的高20%左右,以上4个区域的数据分布情况如图14所示。 Figure 14 Data coverage of 4 different regions图14 4个不同区域的数据覆盖情况 Figure 15 Images rendered from interpolation results of four regions图15 4个区域的插值结果渲染图 基于上述环境,采用本文所述方法框架得到的插值结果如图15所示。完成以上4个区域插值的整体耗时如图16所示。 Figure 16 Comparison of time consumed by interpolation in four different regions图16 4个不同区域的插值耗时对比 由图16可知,虽然陕西与北京的面积、待插值数据量相差20倍左右,但耗时仅相差3倍左右,数据量的增加并未导致耗时等比例增加。主要是因为北京区域的数据规模较小,插值时不能完全利用已有的计算资源,当有少量的数据增加时,更多未被利用的资源开始参与计算,因此陕西相对北京的插值耗时增加不明显。但是,当网格数据量增加到15 638且待插值网格达到2 368时,单台服务器的计算资源已难以支撑,更多的计算节点开始参与插值,耗时显著增加,但增加幅度仍远小于数据量的增长幅度。当区域尺度由新疆扩大到全国时,网格数据量增加了4倍左右,待插值网格增加了10倍左右,但耗时仅增加了5倍左右,说明本文所设计的方法框架针对大区域尺度的插值具有良好的并行加速效果。 以上4个地区在不同任务阶段的耗时对比如图17所示。4个区域最终的栅格化(T5)都没有超过0.1 s,与其他阶段耗时差异太大,故未在图17上展示该阶段的耗时。由图17可知,4个阶段耗时最多的是T2阶段,该阶段需要计算相邻数据点两两之间的距离和协方差并缓存至Redis,时间复杂度约为O(n2),计算量大且有较多的I/O开销;T3与T4阶段主要操作对象为待插值网格,其数量少于数据网格,且其中近邻筛选与插值可以通过简单计算或缓存查询直接完成,时间复杂度约为O(n),因此耗时均小于相同区域的T2阶段的。 Figure 17 Comparison of time consumed at different stages in four test regions图17 4个测试区域在不同阶段的耗时对比 本文选取Spark作为对比框架。Spark是一种基于分布式内存的大数据分析处理框架,支持交互式的数据查询与大批量任务的并行执行,GeoSpark对Spark进行了扩展,使其具有了大规模时空数据处理能力[30]。图18展示了GeoSpark与本文所用网格化方法在时空数据检索阶段(T1)的效率对比。由图18可知,本文所采用的方法在4个区域上的检索效率均高于GeoSpark的,而且区域越大,本文所述方法的效率优势越明显。 Figure 18 Comparison of time consumed between GeoSpark and the proposed method图18 GeoSpark与本文并行时空检索方法耗时对比 考虑到基于矩阵的批量插值模式需要大内存的支持且不适合不规则的大区域,所以基于Spark的插值依然采用先计算距离/协方差并缓存然后逐点插值的流程。全局距离/协方差计算(T2)、近邻点筛选(T3)和半变异函数拟合并插值(T4)3个阶段在Spark上的实现方式如图19所示。 Figure 19 Flow of Kriging interpolation based on Spark图19 基于Spark的Kriging插值流程 Spark主要通过数据分区后独立并行计算来提升计算效率,而距离/协方差计算需要大量交叉运算,难以直接分成独立的数据块。为此在计算之前,本文将所有数据网格通过两两组合的形式形成图19b所示的四元组;然后再由Spark进行并行计算,后续的近邻查询、半变异函数拟合与插值仍采用本文所述的方法,具体的子任务由Spark负责调度执行。基于Spark完成以上操作的耗时如图20所示。 Figure 20 Comparison of time consumed between Spark and the proposed method图20 本文方法与Spark插值耗时对比 由图20可知,在大区域尺度上,本文方法相对Spark具有明显的效率优势,原因主要有2个:(1)在计算距离协方差时,本文采用的分行链式存储结构可以有效地结合距离范围限制参与计算的数据量,而Spark的分块计算模式难以利用该条件;(2)在后续Kriging插值阶段,Spark自身的内存计算、弹性数据集等技术难以对逐点插值的计算流程进行加速,而其内部复杂的任务调度、监控等操作增加了任务之外的额外开销。 碳卫星数据是进行碳排放和碳追踪研究的重要数据源,但在大区域尺度上基于Kriging算法进行插值时计算量很大,而且难以直接进行并行加速。为此,本文以常用OCO-3卫星数据为例,设计了一种DAG结构的Kriging插值工作流,并实现了可对其并行加速的双层分布式调度引擎,通过调整插值过程、细化插值粒度以及优化其中的近邻查询、距离/协方差计算等关键环节使该工作流可以在分布式环境下快速执行。实验结果表明,本文方法框架可以高效完成不同区域尺度上的OCO-3快速插值,在大区域尺度上,相对Spark也具有明显的速度优势。后续将进一步探索更多碳卫星观测数据,研究不同碳卫星数据的融合方法,形成一套更加准确高效的碳卫星观测数据插值融合框架。6 插值任务的分布式并行加速
6.1 工作流任务模块划分


6.2 分布式调度执行与时序控制

7 实验与结果分析
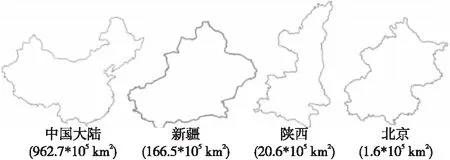





8 结束语

