CAES储气库衬砌开裂对裂隙围岩两相渗流和传热特性的影响

万 发,蒋中明,李海峰,梁贤浩

(1.长沙理工大学 水利与环境工程学院,长沙 410114; 2.珠江水利委员会 珠江水利科学研究院,广州 510000)

0 引 言

压缩空气储能(Compressed Air Energy Storage,CAES)技术是解决当前清洁能源间歇性和不稳定性的关键技术[1-2],在风能、光伏发电持续迅速推广下,CAES技术在国内外一直备受关注[3]。目前CAES储气库多采用地下空腔(盐岩或硬岩洞穴),由于盐岩选址局限,硬岩洞穴、废弃矿洞或人工内衬洞室成为解决该局限问题的较理想方案[4]。

CAES储气库的安全稳定性及密封性是研究CAES技术的关键问题,而解决关键问题的前提是了解运行过程中储气库内压缩空气的热力学过程,在此方面Kushnir等[5],Raju等[6]分别基于围岩传热和绝热假设建立了压缩空气热力学解析解数学模型,He等[7]在研究储气库能量存储时推导了等温、绝热和传热洞壁条件下的压缩空气热力学解析模型,Xia等[8]在Kushnir等[5]研究的基础上提出了洞室内部温度压力的简化解析解,刘澧源等[9]基于Kushnir等[5]成果提出了压缩空气热力学过程的差分算法,万发等[10]则提出了热力学过程的数值计算方法。同时,在储气库衬砌围岩在热力耦合作用下的稳定性问题也有Rutqvist等[11]建立了储气库在热流固耦合作用下的储气库稳定性数值模型,周舒威等[12],蒋中明等[13],夏才初等[14]等基于研究了热力耦合作用下的储气库稳定性。此外,在密封性研究上,Kim等[15]指出储气库内气体会在衬砌密封初始缺陷或反复膨胀收缩产生的裂缝中发生泄漏,周瑜等[16]则对储气库内衬洞室的泄漏进行了研究。

上述研究过程极少考虑地下水对储气库压缩空气渗流的影响,也未对衬砌密封层开裂后裂隙围岩中两相流的渗流传热规律进行研究。当衬砌密封层开裂时,压缩气体和地下水会在衬砌裂缝、薄弱连接处以及围岩裂隙中发生两相渗流和传热作用。

为研究CAES储气库衬砌开裂对裂隙围岩内两相渗流传热特性影响。本文基于COMSOL数值仿真软件中的弱形式PDE(Partial Differential Equation)二次开发了双重介质两相流模型,并联合双重介质传热模型和压缩空气热力学解析模型,建立了CAES地下储气库裂隙围岩双重介质两相渗流传热模型。计算了包括初始充气循环在内的210个运行循环中,衬砌开裂和无开裂2种工况下裂隙围岩水气两相渗流传热过程。

1 储气库裂隙岩体两相渗流传热理论

裂隙岩体中的空隙空间包括岩块中的空隙空间和裂隙空间两部分。空隙和裂隙空间的流体可以相互交换,因此,裂隙岩体的真实渗流状态可以采用裂隙孔隙双重介质渗流模型进行模拟。对于压缩空气地下储气库来说,裂隙围岩中的流体包括水和气体两种介质,其渗流为两相流形态,因此,应采用两相渗流理论进行分析。两相达西理论模型是较为便利的分析多孔介质两相渗流的理论模型,广泛被运用于石油工程[17-19],电池化学[20]等领域。孔隙介质中两相渗流过程可采用COMSOL现有模块建模,但裂隙两相渗流过程需进行二次开发。

1.1 孔隙介质两相流理论

由多孔介质内流体的质量守恒和达西定律可以得出

(1)

其中:

式中:θ为多孔介质孔隙率;s1、s2为流体1和流体2的饱和度,s1+s2=1;u为流速矢量矩阵(m/s);ρ为流体密度(kg/m3);ρ1和ρ2分别为不同相的流体密度(kg/m3);μ为流体动力黏度(Pa·s);μ1和μ2为不同相流体的动力黏度(Pa·s);k为多孔介质渗透系数(mD);kr1和kr2分别为相对渗透率;λ为Corey模型孔隙大小分布指数。

对单元体积内湿润相流体流动,根据毛管力驱动可得

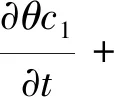
(2)

其中:

式中:c1为流体含量(kg/m3);pc为毛细管压力(Pa),为饱和度s1的函数;pec为毛细管入口压力(Pa)。

由式(1)、式(2)和状态变量方程化简组合可得压力和流体含量的方程组为:

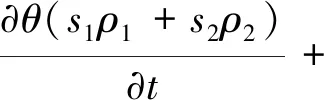
∇p(s1ρ1+s2ρ2)]=0 ;

(3)

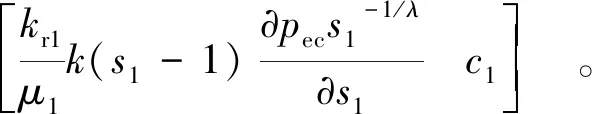
(4)

1.2 裂隙介质两相渗流理论

根据两相流体在裂隙介质中质量守恒和毛细管压力理论可得

(5)

式中:θf为裂隙通道内孔隙率;df为裂隙开度(m)。

裂隙通道内两相流体之间关系和辅助方程均同上,因此可得关于裂隙介质流体渗流压力以及饱和度方程

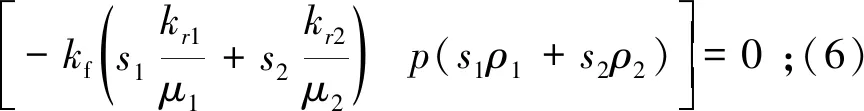
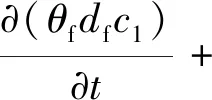
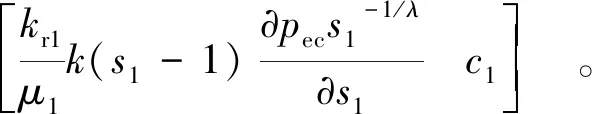
(7)

裂隙中的两相渗流方程组求解p和c1(s1),采用弱形式PDE(Weak Form)方程组进行二次开发建模,流程如下:

(1)先定义边界计算变量,该计算变量用于计算裂隙内两相渗流相关各种状态变量,变量的定义需注意为孔隙介质可识别变量,这样可使得孔隙介质与裂隙介质之前进行流量交换,变量计算逻辑为对两相渗流方程本构的拆解;

(2)再通过边界弱形式及试函数test(p)和test(c1)来构建自定义变量之间计算关系。

1.3 双重介质渗流传热理论

渗流过程往往伴随着热量传递过程,此处采用局部热平衡假设,假设基质和气体温度在极短时间内达到热平衡状态,渗流传热控制方程为

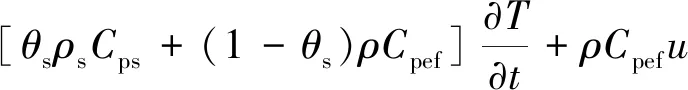
∇[θsks+(1-θs)kef]∇T=Q。

(8)

式中:θs为多孔介质内基质体积分数,无因次;ρs为基质材料密度(kg/m3);Cps为基质材料恒压热容(J/(kg·K));Cpef为流体有效比热容(J/(kg·K)),Cpef=s1Cp1+s2Cp2,Cp1和Cp2分为流体相1和2的比热容;T为温度(K);u为孔隙内气体流动速度(m/s);∇T为温度梯度(K/m);ks为固体基质导热率(W/(m·K));kef为流体有效导热率(W/(m·K)),kef=s1k1+s2k2,k1和k2分别为流体相1和2的导热系数;Q为热源(J/(m3· s))。

裂隙内两相渗流传热理论方程为

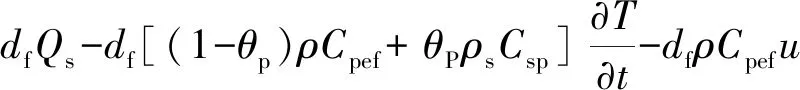
∇t[df(1-θp)kef+θpks]∇tT=0 。

(9)

式中:df为裂隙宽度(m);Qs为流入热量(J);θp为裂隙内固体材料体积分数;▽tT为裂隙内温度梯度(K/m)。

1.4 储气库压缩空气热力学理论

CAES储气库充放气循环会导致压缩空气热力学状态处于循环变化过程中,充气时气体压缩,空气压力和温度升高,放气时压力和温度迅速降低。根据He等[7]研究结果,CAES储气库压缩空气热力学过程可采用以下理论模型进行计算:

(10)

(11)

(κ-1)hcA(Tw-T)] 。

(12)

式中:T为储气库内气体温度(K);min为充气速率(kg/s);CP为气体恒压热容(J/(kg·K));Tin为充气温度(K);V为储气库容积(m3);p为储气库内气体压力(Pa);hc为气体与洞壁对流换热系数(W/(m2·K));Ac为洞壁对流换热面积(m2);R为气体常数(J/(kg·K));κ为绝热系数;Tw为洞壁温度(K);m为储气库内气体质量(kg);mout、min为放气速率和充气速率(kg/s)。

1.5 双重介质两相流计算程序二次开发验证

为验证双重介质两相流数值模型正确性,以Fahad等[21]进行的可视化裂隙性多孔介质两相渗流试验为验证对象,采用COMSOL两相达西和弱形式PDE模块建立该物理试验相对应的数值仿真模型,并将数值计算结果与实际物理试验所得结果进行对照。试验设置如图1所示,多孔介质中存在两条交叉裂隙,其中A工况为一条裂隙竖直,一条裂隙与之成45°夹角,B工况为两条裂隙成90°夹角。初始时多孔介质和裂隙内被水充满,同时在模型顶部以等流量向内注油,两边为不透水边界,下边界为常压流出边界。验证模型采用参数如表1所示。

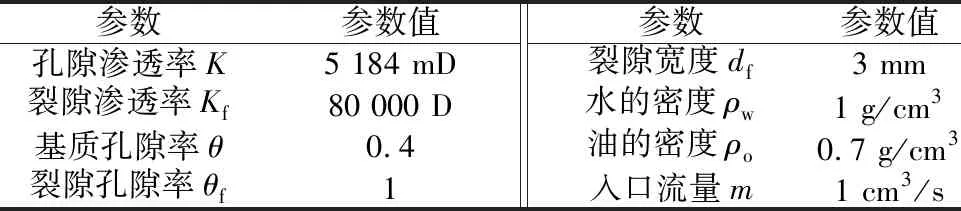
表1 双重介质油水两相渗流验证模型参数

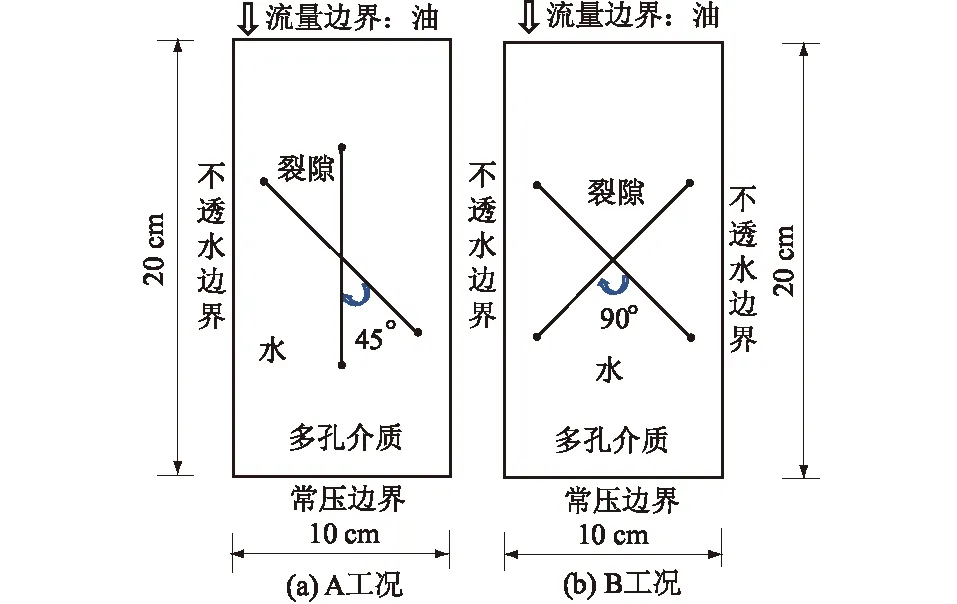
图1 双重介质油水两相渗流验证模型

某时刻裂隙孔隙双重介质油驱水验证模型结果与文献物理试验对比如图2所示,在经过上层多孔介质后,油在裂隙介质中流速较快,形成侵入,因此裂隙及其周围区域油相饱和度高,水相饱和度低。同时在两条裂隙夹角处出现水相饱和度较高区域,数值模拟结果与物理试验所得现象一致性较好。

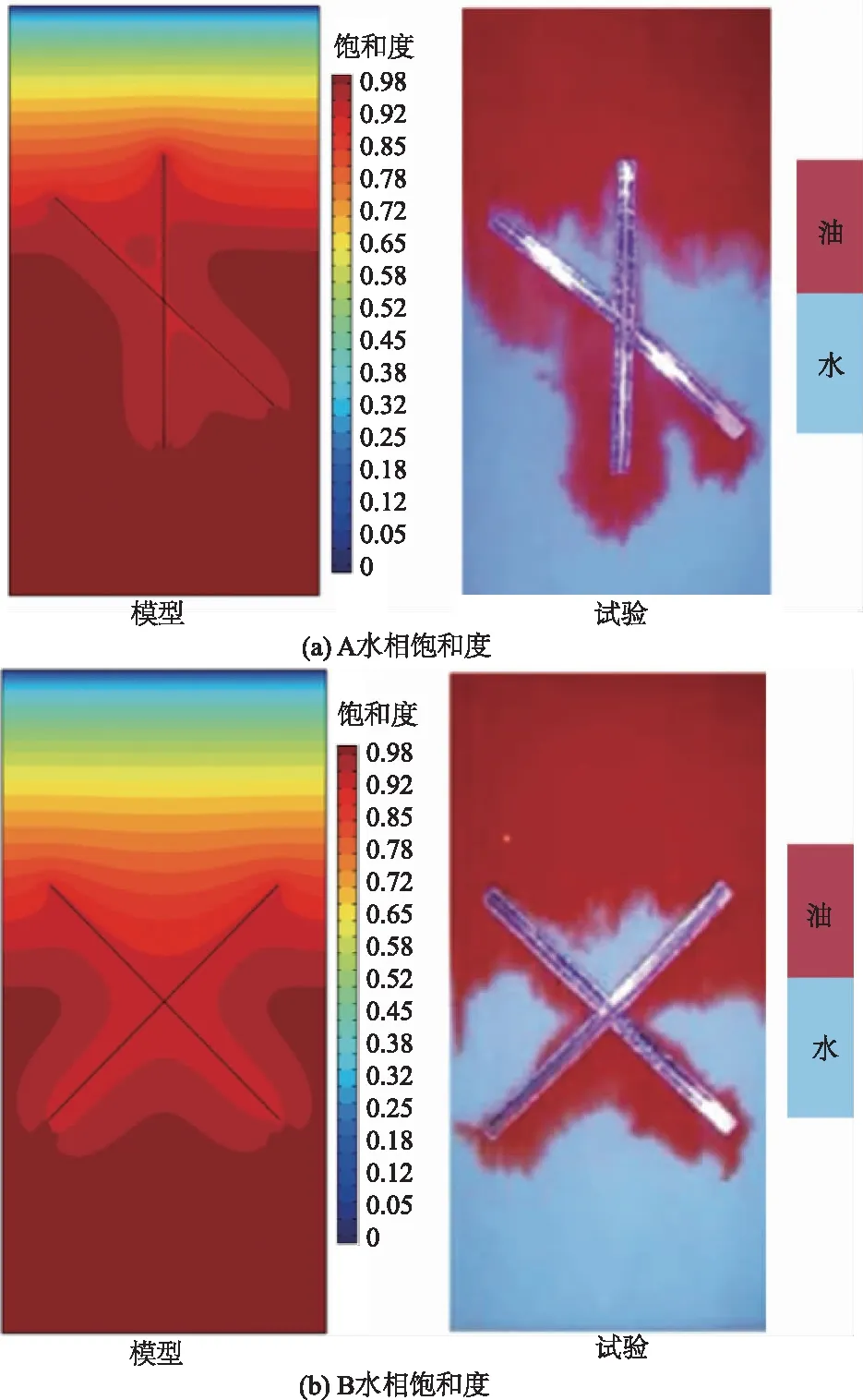
图2 数值模型两相渗流结果与物理试验对比

流体相对渗透率拟合结果如图3所示,数值模型水相相对渗透率与试验拟合良好,油相相对渗透率与试验拟合有所差异,其原因为物理模型本身为较薄的三维结构,且裂隙为真实三维结构,与本文简化后的二维模型存在差异。且文献中油相Corey指数与水相不同,而本文中则使用了同一Corey指数,因此造成了油相相对渗透率拟合差异。综合可证明该双重介质两相流数值模型的正确性。

图3 数值模型流体相对渗透率与物理试验对比

2 衬砌开裂对裂隙岩体两相渗流和传热特性影响

2.1 数值模型的建立

为研究地下水影响下CAES储气库衬砌开裂对裂隙岩体两相渗流和传热特性影响,参考某压缩空气储能电站工程及水文地质条件,设计了如图4所示的计算模型。储气库洞室断面为圆形,计算模型采用1/2断面,尺寸为300 m×300 m,储气库埋深150 m,地下水位线位于地表,围岩为花岗岩,采用低渗混凝土作为衬砌密封层,厚度为50 cm。在储气库围岩中分别设置了3条长度均为27 m的裂隙,裂隙宽度为1 mm。由于衬砌密封层外侧与围岩在施工过程中存在接触作用,并非整体,此处将其视作裂隙考虑,宽度为0.2 mm。此外,根据文献[23]研究结果与本课题组研究成果,衬砌密封层在运行过程中会出现微小裂缝。为研究衬砌开裂对围岩渗流和传热影响,模型分2种工况:① 衬砌密封层设置一条开裂裂缝,宽度为0.4 mm,位于衬砌密封层右上方;② 衬砌密封层完整无开裂。

图4 CAES储气库衬砌围岩两相渗流传热数值模型示意图

计算过程分为两步:① 储气库开挖后,储气库处渗流压力为0 MPa,形成初始稳定渗流压力场;② 储气库运行时,压缩空气的温度和压力随充放气循环变化,驱替衬砌围岩中的水的同时进行传热过程。模型计算参数如表2所示。

表2 CAES储气库衬砌围岩两相渗流传热模型计算参数

模型左边界为对称边界,右边界、上边界和下边界为静水压力边界和水相饱和度边界;对传热模型,右边界、上边界和下边界为温度边界;储气库内壁为空气温度和压力变化的非稳态边界,采用ODE(Ordinary Differential Equation)建模,假定运行过程中储气库内壁气体饱和度始终为1。CAES电站运行周期一般为1 d,一个周期分为4个运行阶段,分别为充气段(8 h)-高压储气段(4 h)-放气段(4 h)-低压储气段(8 h)。初始充气段充气时间24 h,充气速率为52 kg/s,稳定运行充气速率47.5 kg/s,放气速率为95 kg/s。本文模型计算过程为初始阶段和随后的正常运行210 d,其非稳态边界计算结果如图5所示。

压缩空气压力始终处于在7～10 MPa的运行区间内循环变化,初始充气时空气被剧烈压缩,温度迅速升高,放气时温度迅速降低,运行过程中再次充气时由于气体压力变化幅度低于首次充气,气体压缩比例降低,温度升高幅度较低,同时由于洞壁导热作用,空气温度逐步降低,最后形成稳定波动状态,稳定运行时温度变化范围为272～303 K。

2.2 衬砌开裂对裂隙围岩渗流压力和饱和度影响

210 d时典型运行阶段2种工况下裂隙围岩的渗流压力分布如图6所示。

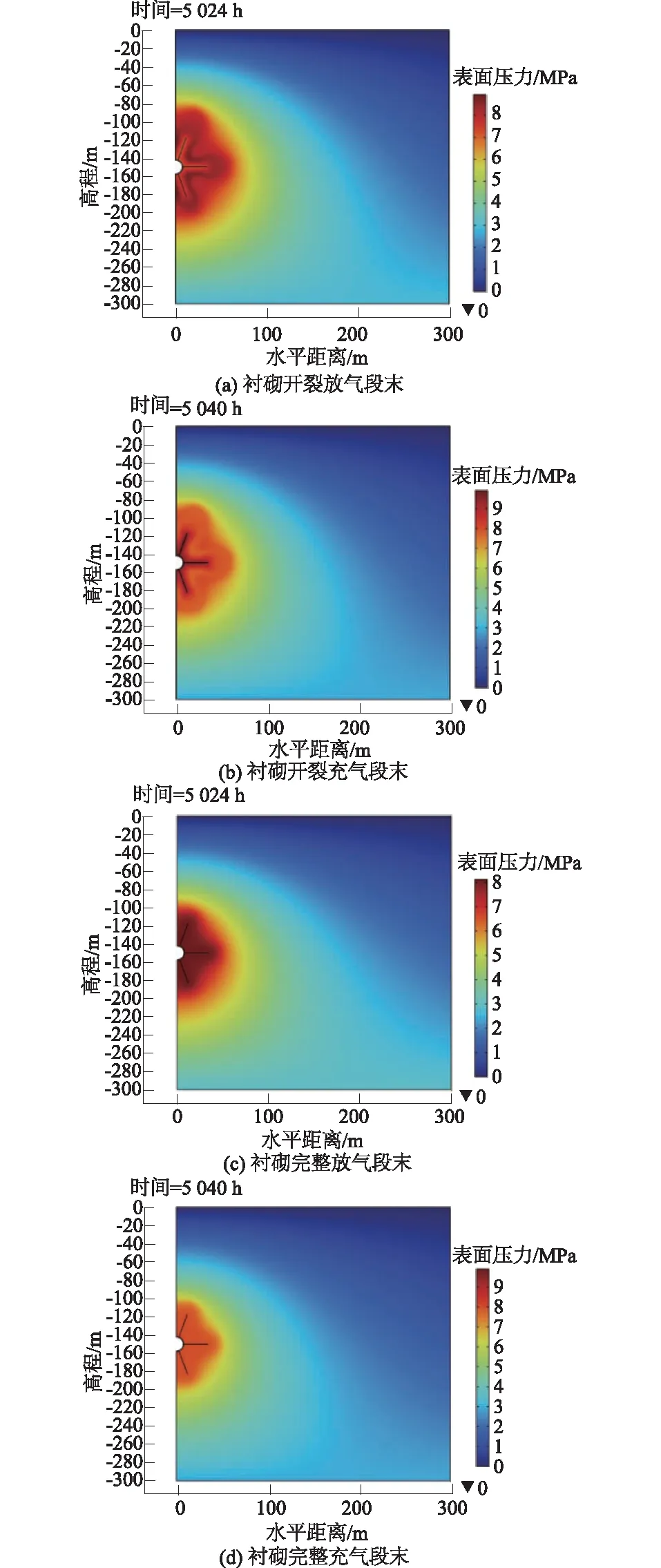
图6 210 d典型运行阶段裂隙围岩内渗流压力分布

衬砌开裂的模型中围岩裂隙和孔隙内渗流压力差异显著,距洞壁相同距离的最大压力差异为1.9 MPa;而不考虑开裂的模型围岩裂隙与孔隙内渗流压力分布较为均匀,相同距离最大差异为0.4 MPa。开裂模型中,充气末围岩裂隙渗流压力为9.6 MPa,渗流压力>8 MPa的区域从裂隙尽头向围岩延伸10.2 m,充气和放气段末围岩裂隙渗流压力相差3 MPa;在无开裂模型中,充气末围岩裂隙渗流压力为8.03 MPa,>8 MPa渗流压力范围仅延伸1.2 m,充气和放气段围岩裂隙最大差异只有0.18 MPa。值得注意的是放气阶段储气库气体压力迅速降低,但2种模型围岩内仍然保持较高渗流压力,存在渗流迟滞效应。对比两个模型的计算结果,表明衬砌开裂会显著影响围岩内渗流压力分布,影响主要体现在压力分布均匀性、高渗压传递范围,以及围岩裂隙和周围孔隙内渗流压力的高低。

分别对围岩裂隙方向和多孔介质方向取截线,两种模型在不同运行阶段各截线渗流压力分布如图7所示。

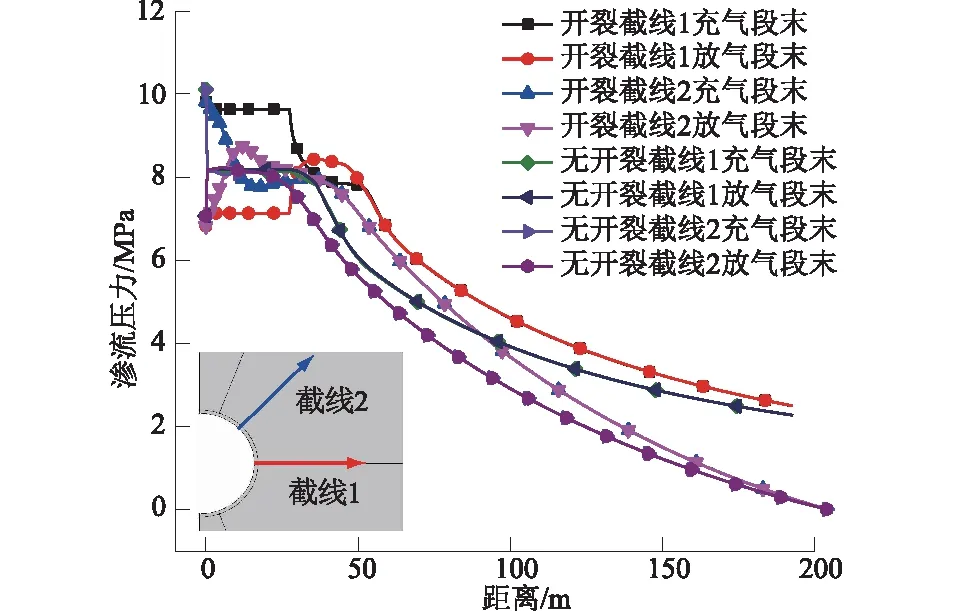
图7 围岩裂隙和多孔介质渗流压力分布

在时间、距离均相同的条件下,开裂模型的裂隙和孔隙内渗流压力总体高于无开裂模型。截线1的充气和放气段渗流压力分布线在开裂模型中于52 m之后重合,而在无开裂模型中则于37.5 m后重合,截线2的充放气渗流压力在开裂模型中距离约30 m后重合,在无开裂模型重合距离缩小为16 m。由此可知开裂后模型围岩内渗流压力随充放气过程循环变化的范围为52 m,无开裂时该变化的范围为37.5 m,开裂模型中多孔介质渗流压力受充放气影响范围为30 m,无开裂模型中该影响范围为16 m。因此,衬砌开裂后不仅会造成围岩内裂隙和孔隙内渗流压力升高,而且会使渗流压力受充放气过程而波动变化的范围大幅扩大,在本模型计算中,增长幅度可达46.7%。衬砌开裂会导致周围孔隙内渗流压力随运行过程起伏波动更大。

运行210 d后2种模型衬砌和裂隙围岩内水相饱和度分布变化如图8所示,压缩空气主要经裂隙通道驱替地下水,当裂隙通道完全被空气占据后,压缩空气会在裂隙尽头处向附近围岩内入侵。由于围岩裂隙尽头高程不同,渗流压力不同,进而导致渗流速度不同,最终使得3条裂隙尽头处气相饱和度为1的范围有所差异,最上方的裂隙尽头处范围最大,最下方的范围最小。衬砌开裂对气体饱和度影响主要集中在围岩裂隙及其周围。无开裂模型水平方向饱和度整体低于开裂模型,运行210 d后气体扩散范围为54 m,开裂模型运行210 d后水平方向气体扩散影响范围为66.7 m,较无开裂模型扩大了12.7 m。

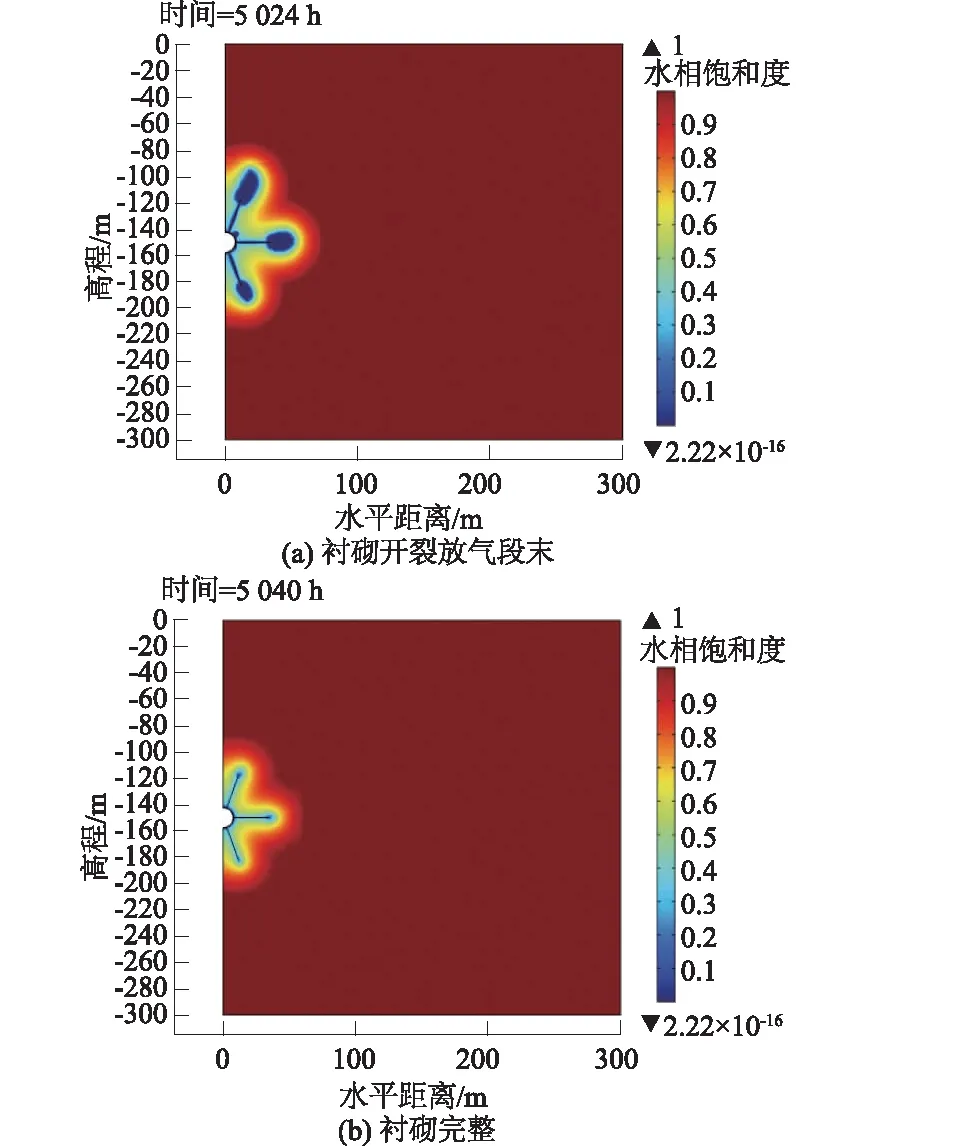
图8 开裂对裂隙围岩水相饱和度的影响

2.3 衬砌开裂对储气库整体泄漏速率的影响

对储气库洞室内边界通过流体进行积分,可得储气库每时刻泄漏速率,计算公式为

me=∮uρDds。

(13)

式中:me为漏气速率(kg/s);D为洞室轴向长度(m);s为洞室横截面周长(m)。

以第200—第210天计算结果为分析对象,两种模型储气库泄漏速率变化如图9所示,储气库充气时内部压力高于双重介质内渗流压力,此时泄漏方向向外,放气时泄漏方向向内。衬砌开裂后的储气库整体泄漏速率低于无开裂时,其原因为衬砌开裂后,由于衬砌裂隙与衬砌围岩的间隙相连,直接导致衬砌外侧渗流压力高于无开裂模型,进而导致洞壁内外压差降低,洞壁处孔隙介质渗流速度相比无开裂模型降低约10倍,尽管开裂点泄漏速率较高,但是其开裂宽度较小导致其流量与储气库整体泄漏率相比仍然低了一个数量级。因此在该模型中,衬砌开裂会使储气库整体泄漏速率降低。但值得注意的是,该结果规律仅在围岩裂隙不与大气相连时适用,当围岩裂隙与大气相连时,衬砌外侧渗流压力与大气压力形成稳定梯度时,开裂泄漏不对衬砌外侧渗流压力造成影响,衬砌开裂将不会对洞壁孔隙介质渗流速度造成影响,此时开裂会使泄漏速率增加,增加部分主要为衬砌裂隙处泄漏量。

图9 开裂对储气库泄漏速率的影响

2.4 衬砌开裂对衬砌及裂隙围岩传热特性影响

2种模型在第210天充气段末的衬砌及裂隙围岩温度分布如图10所示,无论是否考虑开裂,衬砌和裂隙围岩温度分布均呈圆形圈层分布,水平截线和围岩孔隙介质截线温度分布线相重合,因此可知,开裂和裂隙的分布对围岩温度的传递和分布影响非常微弱,其原因是渗流速度较低,同时空气的比热容较小,低流速的空气所含有热能变化较低,因此裂隙的存在不会影响围岩温度的分布。围岩温度与初始值相比最大差异为1 K,平衡运行时温度变化影响范围为20.8 m,影响范围内的围岩温度低于初始温度,远处温度保持初始温度。相比围岩温度分布,衬砌温度梯度较大,充气段末衬砌内外温差为16 K。

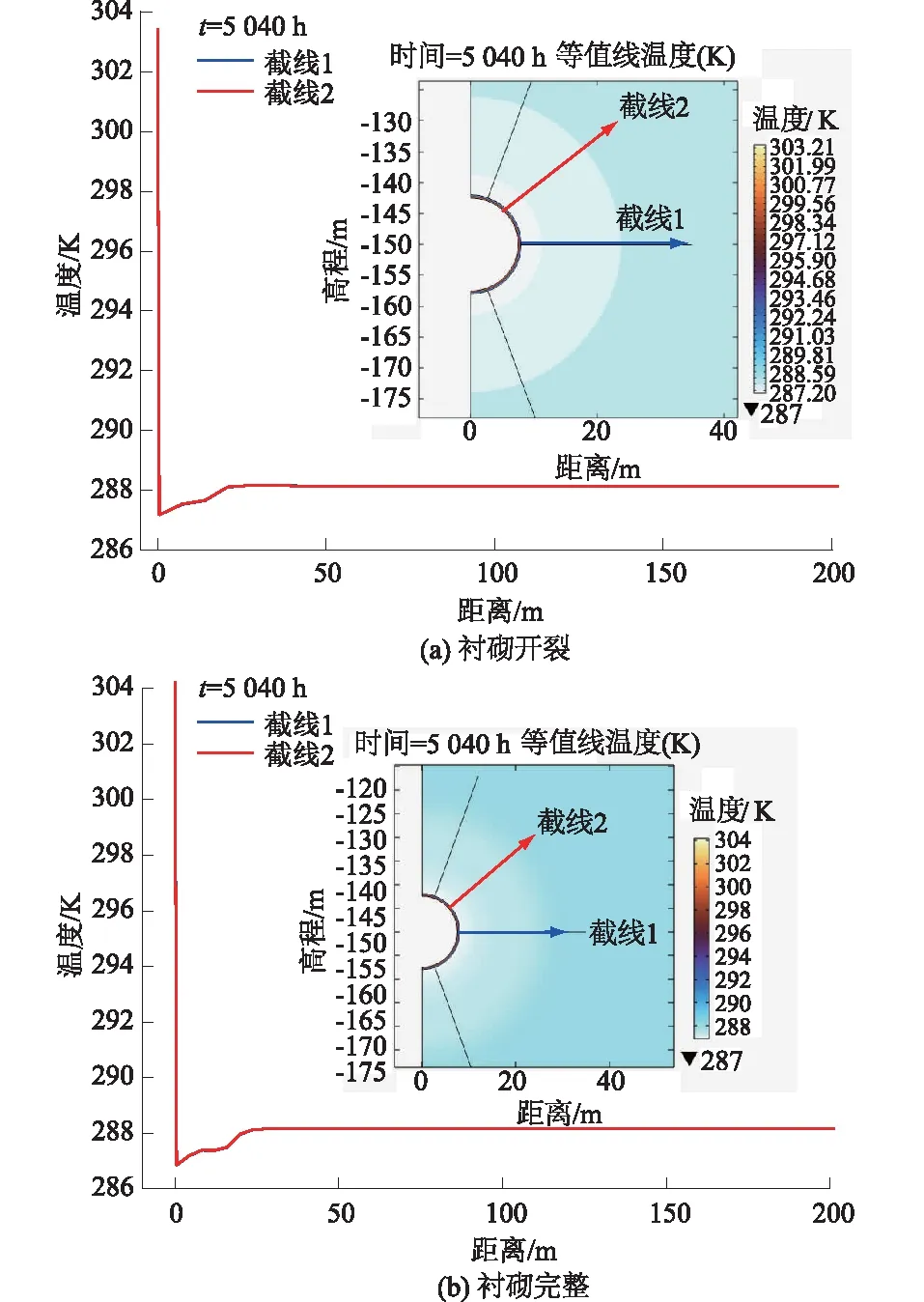
图10 第210天充气段末衬砌和裂隙围岩温度分布规律

温度的分布变化主要集中衬砌密封层内,衬砌不同位置的测点温度变化如图11所示,由图11可知,充放气循环时温度起伏波动变化规律与充放气运行过程相一致,变化幅度则各有差异。衬砌内侧温度变化幅度为31 K,衬砌中间25 cm处温度变化幅度为15 K,衬砌外侧温度变化幅度为1.5 K,起伏变化稍滞后于内侧温度的变化。整个运行过程中,温度的变化都集中于衬砌密封层内,衬砌内侧会受到初始循环的高温作用,此时衬砌内外温差较高,需注意由此产生的温度裂缝。

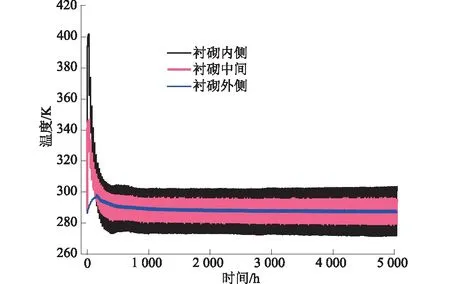
图11 衬砌不同位置温度变化规律

3 结 论

以多孔介质两相渗流理论为基础,采用弱形式二次开发了双重介质两相渗流模型,并进行了验证。同时利用数学模块全局ODE建立压缩空气热力学模型,并耦合多孔介质传热模型,建立了CAES硬岩储气库的裂隙围岩两相渗流传热模型。以某压缩空气储能电站储气库为研究背景,研究了衬砌开裂对电站运行过程中裂隙围岩两相渗流和传热特性的影响。结果表明:

(1)基于弱形式PDE二次开发的双重介质两相流模型可较好地模拟双重介质内两相渗流互驱过程。

(2)衬砌开裂会显著影响围岩内渗流压力分布,主要体现在围岩裂隙和孔隙内渗流压力差增大,最大增加1.5 MPa;围岩裂隙尽头孔隙介质高渗压范围扩大;以及使渗流压力受充放气过程而波动变化的范围放大。

(3)压缩空气从裂隙中向外扩散,并在裂隙尽头处向围岩内驱替地下水,衬砌开裂会导致气体扩散范围显著增加,本模型中210 d气体水平扩散范围由未开裂前的54 m扩大至66.7 m。

(4)衬砌开裂和围岩裂隙的存在对衬砌和围岩的温度分布基本没有影响,2种条件下相同距离裂隙和孔隙介质温度分布一致。围岩的温度变化平稳,稳定运行后其温度起伏变化在1 K内。温度变化主要集中衬砌密封层内,初始循环是衬砌内外侧温差极大,本模型中>100 K,需注意此时不均匀温度造成的温度裂缝。