基于翅片超表面钝体的流致振动俘能特性研究1)

张 野 王军雷

(郑州大学机械与动力工程学院,郑州 450001)

引言

进入21 世纪,随着全球能源消耗的快速增长和储量的急剧下降,传统化石能源越来越难以满足全球发展的需要,同时化石能源的大量使用必然会严重破坏全球环境,也导致地球上低品位的能量大量增加.因此,越来越多的学者致力于开发环境友好型能源,如太阳能[1]、潮汐能[2]和氢能[3]等.近年来,无线传感器网络 (wireless sensor networks,WSNs)和微机电系统 (micro-electro-mechanical systems,MEMs)在日常生活和工业生产中得到了广泛的应用,如何为数以万亿计的微型网络设备不间断地提供电能,以保证其在不断变化的环境中长久运行被广泛认为是世界性的难题之一.在过去的几十年里,无数学者已经证明从周围环境中提取低品位能量是可行的,如热能[4]、辐射能[5]和振动能[6],开发低品位能量不仅可以供应数万亿分布广泛且功耗极低的电子元件,还可以减少化石能源消耗和环境污染.振动俘能作为最有前景的研究领域之一,在近几年得到了广泛的关注,地球上的大气环流引发了众多学者对流致振动俘能[7-9](flow-induced vibration energy harvesting,FIVEH)的探索.压电[10]、电磁[11]和摩擦电[12-13]是3 种最常见的能量转化机制.由于压电俘能器裸机成本低、体积小、操作方便、易于扩展和集成等优点,其被认为是一种具有竞争力的俘能技术,在自动化领域得到了广泛地应用.

流致振动根据振动机制主要分为涡激振动[14](vortex-induced-vibration,VIV)、驰振[15]、颤振[16]和抖振[17]等.由于涡激振动与驰振具有在低流速下有利于能量俘获的振动特性,许多学者对其进行了广泛的研究.为了使基于涡激振动的压电俘能器(VIVbased piezoelectric energy harvester,VIVPEH)在低风速下保持稳定的性能,国内外学者在如何提高低风速下涡激振动压电俘能器的效率方面进行了大量的科学研究.Xu 等[18]使用响应面分析法结合数值模拟来寻找涡激振动最优的俘能效率,可以在一定程度上减少实验次数.Lu 等[19]设计了一种两自由度 (twodegree-of-freedom,2DOF)涡激振动压电俘能器,可以在较低风速下产生两个锁定区域以提高俘能效率.Badhurshah 等[20]数值研究了双稳态弹簧对圆柱体涡激振动能量收集效率的影响,与线性弹簧相比,双稳态弹簧可将涡激振动的俘能效率最大提升1.5 倍.针对相对较高风速和高振幅的驰振,研究人员致力于提高驰振压电俘能器 (galloping-based piezoelectric energy harvester,GPEH)的性能,包括引入非线性力,改变钝体结构.Li 等[21]在钝体周围增加了几个磁铁,提出了一种新型GPEH,可以将起振风速从2.2 m/s 降低到1.8 m/s,并在更大的风速范围内产生更高的电压输出.Wang 等[22]提出了一种锥形悬臂梁,并设计了一种锥形GPEH,与方形截面梁相比,锥形GPEH 的振动幅值降低了44%,输出功率提高了61%.

也有学者在钝体表面引入一些小型附件来改变其气动特性,其原因是增加了钝体的表面粗糙度从而影响了钝体周围的流场.Hasegawa 等[23]研究了使用毛发状超细纤维涂层降低圆柱体阻力的可行性,结果表明超细纤维涂层的角度位置对减阻有决定性的影响.Zhu 等[24]在圆柱体上增加了一对鳍片,实现了从涡激振动到驰振的过渡,输出功率明显增强.Hu 等[25]在方柱的尖角上安装了鳍片,结果表明,在前缘尖角安装鳍片可以使GPEH 的最大功率提高2.5 倍.超表面是一种类似于小型附件的新型表面结构,在天线、光学、声学等领域有着广泛的应用.许多学者试图将人工设计的超表面与压电俘能器结合起来,探索改变俘能器空气动力学特性的可行性.Wang 等[26]数值研究了具有仿生表面的圆柱体的涡激振动响应,发现随着仿生超表面高度的增加,圆柱振动幅度逐渐减小,工作带宽逐渐变小.Sun 等[27]将球型超表面应用于椭圆钝体上,结果表明: 当超表面高度为2 mm 时,俘能器输出功率比光滑椭圆钝体提高了51.86%;而当超表面高度为4.5 mm 时,钝体几乎没有振动.Zhao 等[28]在方柱迎风侧设计了一系列V 型凹槽,发现V 型凹槽能够降低GPEH 的起振风速并显著提升其输出功率.

目前已有国内外学者将超表面结构应用于FIVEH.然而多数研究仅着重研究增强FIVEH 性能的超表面结构,而针对改变超表面结构的高度和数量对FIVEH 性能的影响机制研究相对较少.因此,本文设计了一种带有翅片超表面钝体的FIVEH,通过风洞实验研究了超表面高度和数量对压电俘能器输出电压和振动特性的影响.基于Tamura-Shimada 模型以及基尔霍夫电流定律,建立了压电俘能器流-固-电耦合理论模型,并将理论结果与实验结果进行比较,验证了数学模型的正确性.利用CFD 技术模拟了钝体附近的旋涡脱落过程,获得了不同钝体的流场特性.最后研究了不同接口电路对压电俘能器输出性能的影响.

1 单自由度压电俘能器的理论模型

带有超表面结构的单自由度 (single-degree-offreedom,SDOF)压电俘能器如图1(a)～图1(c)所示,它由钝体、悬臂梁、压电片 (PZT-5)组成.钝体直径为D、高度为H、悬臂梁长Lc、厚Tc、宽Bc,PZT-5 长Lp、宽Bp、厚Tp.其中,PZT-5 固定在悬臂梁一端,悬臂梁另一端则连接钝体,钝体质心到钝体边缘的距离为λD,悬臂梁上端到钝体质心的距离为Lb.PZT-5 外接一个简单负载RL,当流体流经钝体时,在钝体表面产生垂直于来流方向的气动力Fa,使得钝体产生周期往复的运动并带动悬臂梁振动,从而引起PZT-5 产生形变,进而在PZT-5 表面产生感应电荷,感应电荷定向移动形成电流.

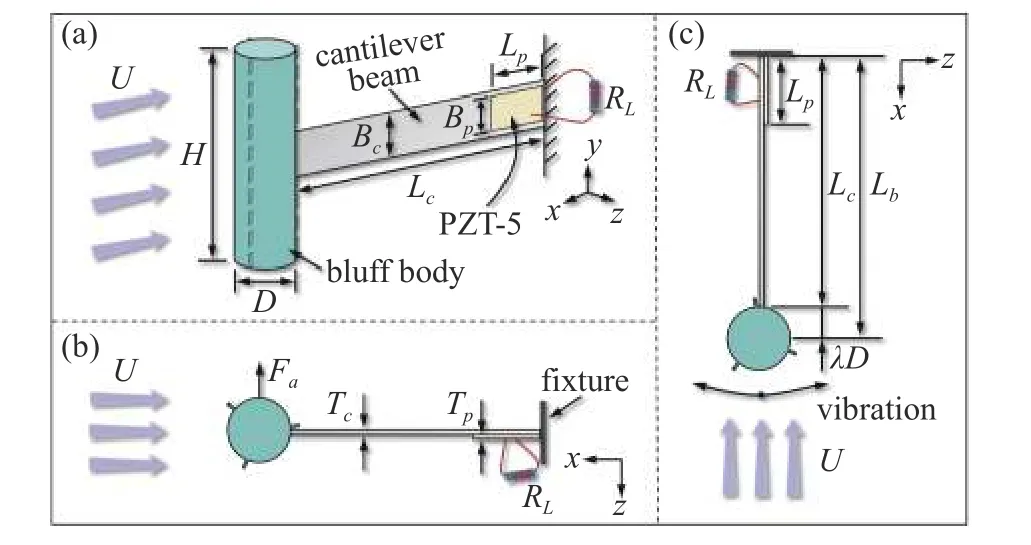
图1 带有超表面结构的压电俘能器示意图.(a)结构示意图,(b),(c)俯视图Fig.1 Schematic of the proposed FIVEH with metasurface.(a)Sketch of structure,(b),(c)top view

根据图1,可使用拓展的哈密顿原理 (the extended Hamilton’s principle)推导SDOF 压电俘能器的控制方程

式中,δT,δP,δWV分别表示在t0到t1的时间间隔内压电俘能器总动能、总势能以及非保守力做的虚功的变化量.

压电俘能器的总动能可以表示为

式中,mp=ρpBpTp为单位长度PZT-5 的质量,mc=ρcBcTc为单位长度悬臂梁的质量,m1为钝体的质量,u(x,t)为悬臂梁在t时刻坐标x处的位移.在环境风激励的条件下,俘能器的一阶模态占主导地位,因此,下文只考虑俘能器的一阶振动模态.通过分离变量,u(x,t)可改写为u(x,t)=φ(x)Z(t),φ(x)为梁的一阶模态函数,Z(t)为一阶模态坐标,Im为钝体绕质心偏转的转动惯量.

压电俘能器的总势能[29]可表示为

式中,E1I1为悬臂梁的抗弯刚度,E2I2为0 到Lp处附着PZT-5 处悬臂梁的抗弯刚度,Θ为机电耦合系数,V(t)为RL两端的电势差,Cp为PZT-5 的夹持电容.

非保守力做的虚功可表示为

式中,Q为通过负载的电荷量,ca为空气阻尼系数,cs为梁结构的黏性阻尼系数,Fa为钝体受到的总气动力.假设钝体为悬臂梁下端的一个质点,则有

气动力Fa对钝体做的虚功[30]为

对于一般钝体,流体在钝体质心上施加的气动力Fa既包含驰振力,也包含涡激振动力.其中

式中,i=1,3,5,7.f是涡驰耦合系数,是一个与钝体形状相关的常数,对于完全表现驰振的钝体来说f=0,q(t)是钝体后方的尾流倾角,Ai是与驰振相关的气动力系数,对于完全表现涡激振动的钝体来说Ai=0.如图2 所示,一般使用Tamura 和Shimada 提出的涡驰耦合模型 (Tamura-Shimada 模型)[31-33]来描述钝体后方的尾迹动力学行为

图2 攻角与气动力示意图Fig.2 Schematic of attack angle and aerodynamic forces

式中,β是尾流振子的阻尼比,ωVIV是尾流振子的固有频率,CL0是气动升力系数的幅值,γ是从Tamura-Shimada 模型中导出的参数,St是斯特劳哈尔数.联立式(7)与式(9)可得

式中,=A1–CD为驰振力系数的第一项,决定了钝体驰振的起振风速,是一个常数,下文中可直接用A1替换.

如图3 所示,对于单自由度压电俘能器,可简化为质量-弹簧-阻尼系统,其控制方程为

式中,Meff为等效质量,Ceff为等效阻尼,Keff为等效刚度,可通过以下公式计算

式中,m2=mpLp+mcLc为PZT-5 与悬臂梁的总质量,fn为压电俘能器的固有频率,ζ为压电俘能器的阻尼比,fn与ζ都可以通过自由衰减实验得到.

机电耦合系数Θ表征了压电材料将振动能转化为电能的能力,可通过以下公式计算

式中,fon为压电俘能器的开路频率,一般与fn相等,当外接负载足够小时,电路接近短路,通过自由衰减实验可获得压电俘能器的短路频率fsn.

可在PZT-5 两端连接不同类型的能量采集电路,这里首先假设外接一个简单负载RL,因此对于PZT-5 一侧,由基尔霍夫电流定律可得

联立式(10)～式(14)及式(19)并无量纲化可得

以上3 式中,τ=ωnt,z(τ)=Z(τ)/D,Sn=2πSt,γ=D/(H+λD),η=ωVIV/ωn=SnU/(Dωn),θ=Θ/(ωn2Meff·D),χ=ρD2H/(2Meff),()′=d()/dτ=ωnd()/dt,ωn=2πfn.

2 压电俘能器的实验设置与CFD 设置

2.1 压电俘能器的实验设置

如图4 所示,在圆柱钝体表面添加了不同列和不同高度的翅片超表面.从图4(a)～图4(d),超表面逐渐从1 列 (R1)增长到4 列 (R4),高度逐渐从1 mm (h1)增加到7 mm (h7),组成了16 组不同的钝体 (R1h1～R4h7).每一列有10 个翅片,相邻翅片中心距为12 mm,翅片宽度为8 mm,第一列翅片与钝体水平中心线的夹角为50°,其余列翅片则等角度分布在钝体表面,结合图1 和图4,整个钝体居中安装在悬臂梁的自由端.钝体直径D为32 mm,高度H为120 mm,悬臂梁尺寸为Lc×Wc×Tc=160 mm×25 mm×0.5 mm,PZT-5 尺寸为Lp×Wp×Tp=30 mm×20 mm×0.5 mm,PZT-5 由少量丙烯酸固定在悬臂梁的固定端,PZT-5 与悬臂梁的总质量m2为10.82 g,钝体质量m1统一为3.2 g.

图4 带有不同列数与不同高度的翅片超表面钝体Fig.4 Finned metasurface bluff bodies with different rows and different heights

如图5 所示,整个实验装置放置在直径为400 mm的开放式风洞中,风洞长度为 4700 mm,蜂巢结构与整流板放置在风洞入口处,用于稳定环境风,压电俘能器放置在风洞末尾的测试段,双通道虚拟示波器(ISDS220B)用于测量俘能器产生的电压,高精度激光位移传感器 (HG-C1400)用于测量钝体的位移,高精度热线风速仪 (Testo Co.,USA)用于测量风洞内风速,三相变频器 (RP350)用于控制风洞风速,风速U与变频器频率f之间的关系为U=0.137f+0.18.光滑圆柱与光滑方柱为对照组,其余4 组共16 个钝体为实验组,每次实验结束后更换悬臂梁自由端的钝体即可.

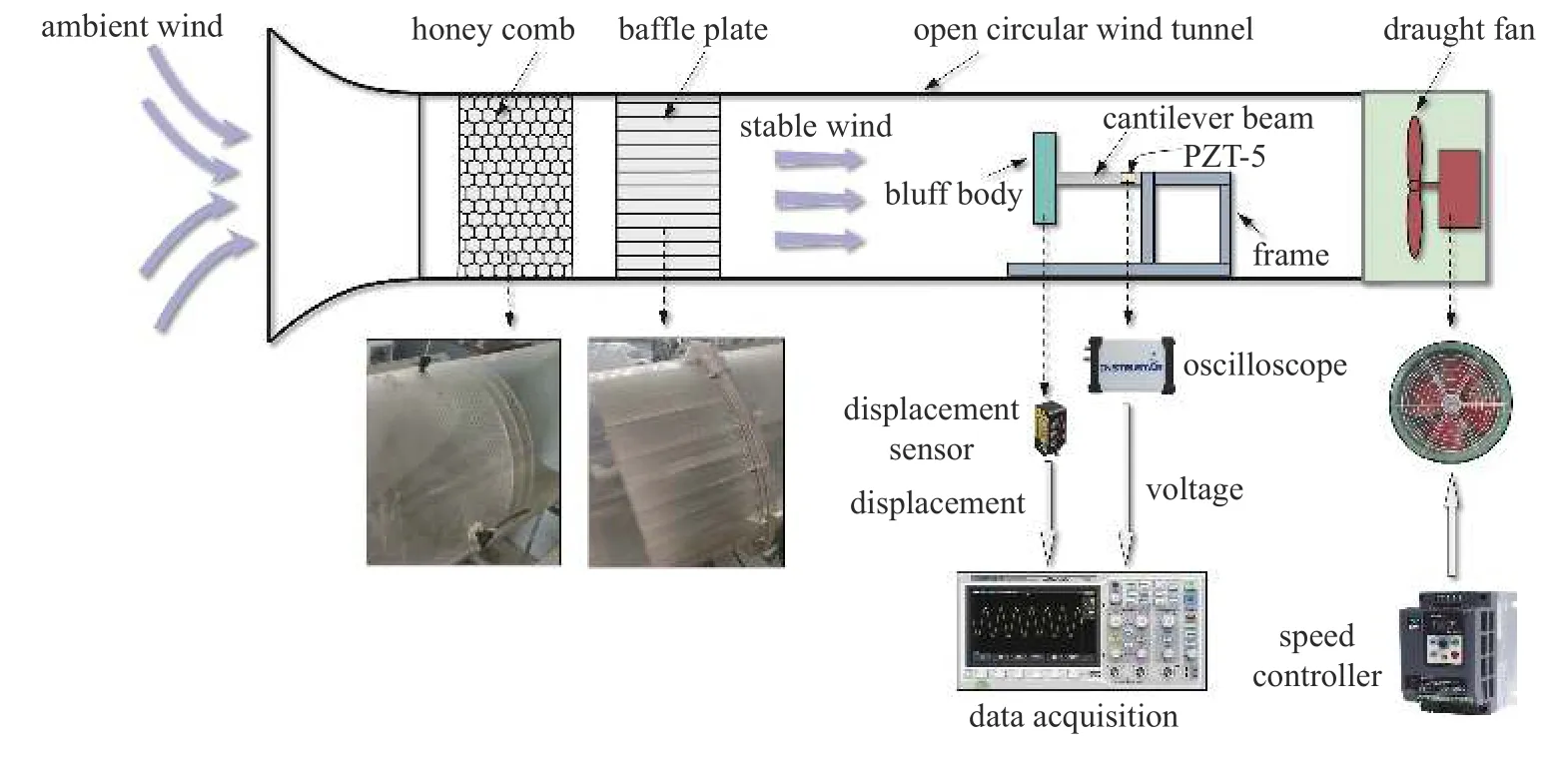
图5 实验布置Fig.5 The experiment setup

如图6 所示,以光滑圆柱为例,通过自由衰减实验可获得压电俘能器的固有频率fn,而在PZT-5 两端接入一个较小的负载RL则可获得压电俘能器的短路频率fsn.

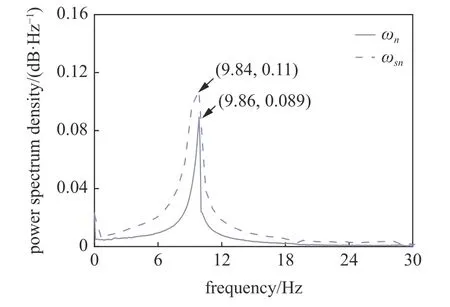
图6 压电俘能器的固有频率与短路频率Fig.6 The natural frequency and short circuit frequency of piezoelectric energy harvester

2.2 压电俘能器的CFD 设置

本文使用基于格子玻尔兹曼方法[34](lattice Boltzmann method,LBM)的商业软件 XFlow (北京树优信息技术有限公司提供技术支持服务)模拟钝体的气动力系数.如图7 所示,以单自由度钝体为例,计算域尺寸为35D×20D×3.75D,钝体到左侧入口的距离为10D,到右侧出口的距离为25D,纵向阻塞率为D/(20D)=5.00%,不超过6%[35],满足计算要求.

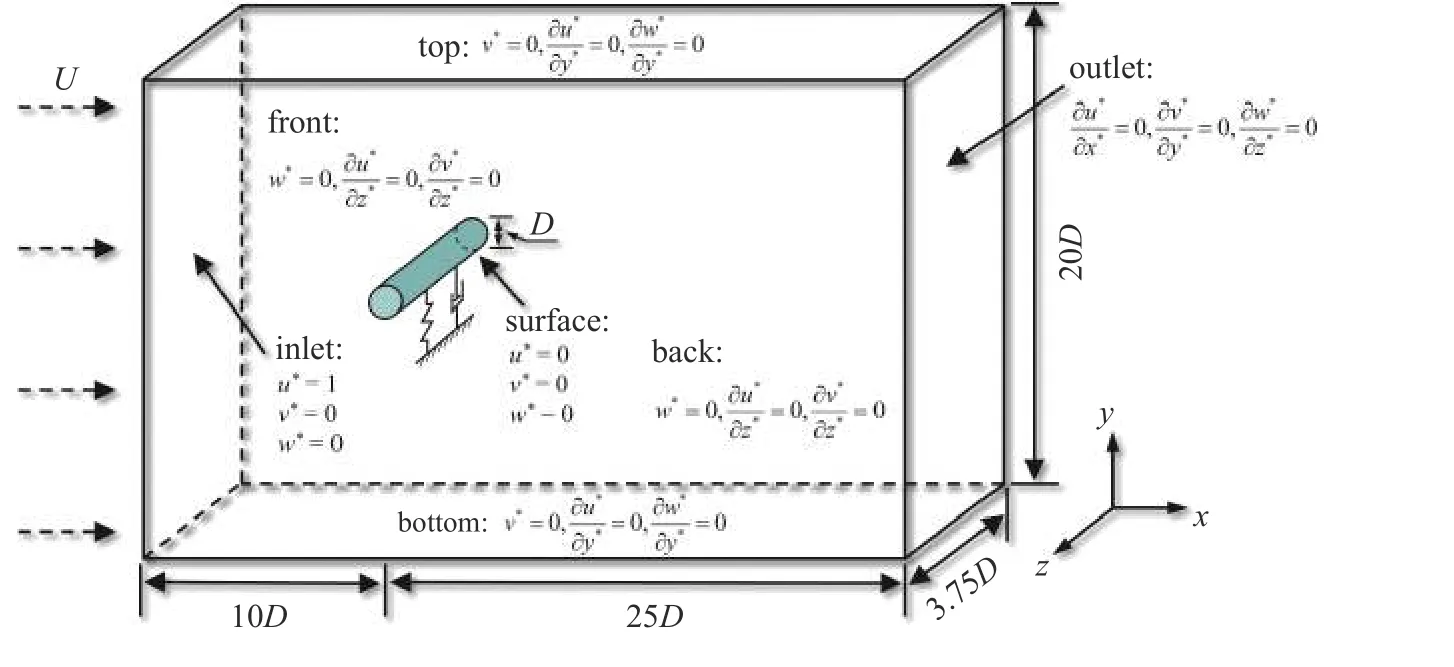
图7 计算域与边界条件Fig.7 Computational domain and boundary conditions

引入以下无量纲参数:u*=u/U,v*=v/U,w*=w/U,t*=tU/D,x*=x/D,y*=y/D,z*=z/D,p*=p/(ρU2),Re=ρUD/μ.式中,u,v,w为风速U在笛卡尔坐标系中对应的3 个分量,μ为流体的动力黏度,对于空气,μ一般取1.79×10-5Pa·s.

计算域左侧设置为流动进口,右侧设置为流动出口,上下前后边界设置为对称边界,钝体表面设置为无滑移壁面.对于三维不可压缩流动,无量纲控制方程如下.

质量守恒方程

动量守恒方程

单自由度钝体的运动依然由无量纲质量-弹簧-阻尼方程来控制,则在y方向上

式中,Y=y/D为钝体的无量纲位移,Ur=U/(fnD)为折减速度,CLm=2FLm/(ρU2D)为模拟出的气动力系数,m*=4Meff/(ρπD2)为质量比.与式(14)相比,式(27)忽略了机电耦合力ΘV(t),且钝体受到的总气动力Fa则由模拟出的气动力FLm替换.

以SDOF 圆柱为例进行晶格无关性验证并确定CFD 模拟的晶格尺寸.设定风速U=1.687 m/s,此时Re=3700,钝体后方的涡街由层流转变为湍流[36],因此,采用大涡模拟 (large-eddy simulation,LES)方法,选择XFlow 内置的Smagorinsky 模型用于模拟钝体气动力与流场中的旋涡结构,该模型在计算钝体气动力方面具有较好的准确性[37].如图8所示,整个计算域由相互正交的晶格组成,为保证晶格的准确性,采用了3 种不同数量的晶格 (粗糙—L1,中等—L2,精细— L3)进行晶格无关性验证,它们的数量分别为1 198 913,1 381 446,1 790 129,时间步长设置为 “fixed-automatic”.

图8 计算域晶格示意图Fig.8 Schematic of computational lattice

如表1 所示,对仿真来说,CDmean为钝体受到的气动阻力系数的平均值,CLrms为钝体气动升力系数的均方根 (root-mean-square,RMS),Ymax为钝体在y方向上的无量纲振幅.L2 与L3 晶格之间的最大误差没有超过7.00%,为了提高计算效率,选择L2 晶 格尺寸用于CFD 模拟.

表1 晶格无关性验证结果Table 1 Results of lattice independence verification

3 结果与讨论

3.1 实验结果讨论

图9 首先给出了两组对照组的风洞实验结果,包括RMS 电压Vrms以及振幅

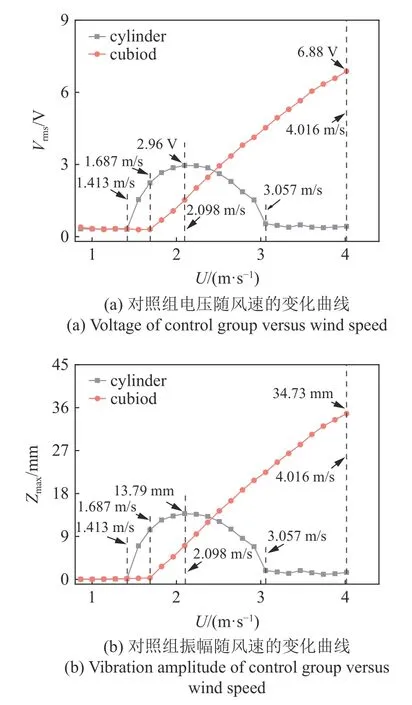
图9 对照组风洞实验结果Fig.9 Wind tunnel test results of control group

对于圆柱来说,其表现出典型的涡激振动,起振风速为 1.413 m/s,工作带宽为1.413～3.057 m/s,最大RMS 电压为2.96 V,最大振幅为13.79 mm,都出现在2.098 m/s 处.方柱则表现出经典的驰振,起振风速为1.687 m/s,随后RMS 电压与振幅都随风速的增大而增大.最终,方柱最大RMS 电压为6.88 V,最大振幅为34.73 mm,都出现在4.016 m/s 处.与圆柱相比,方柱的最大RMS 电压提高了132.43%,振幅则提高了151.85%.

图10～图13 给出了实验组的风洞实验结果.总体来说,翅片超表面高度较低时对钝体振动有抑制作用,比如R1h1,R2h1,R3h1,R4h1 等.与圆柱相比,这些钝体可以通过缩小工作带宽或者抑制振幅来抑制涡激振动.而当翅片超表面高度足够高时,大部分装配了翅片超表面的钝体振动特性都不同于涡激振动,比如R1h5,R2h3,R3h5,R4h7 等,这些钝体的振幅和RMS 电压变化与方柱类似,都随风速的增加而增加.

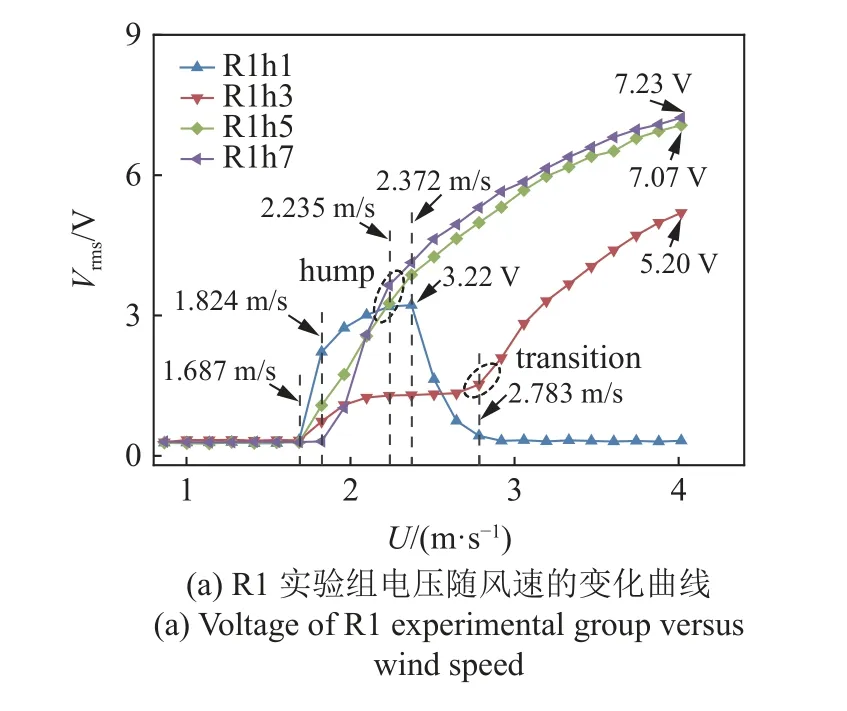
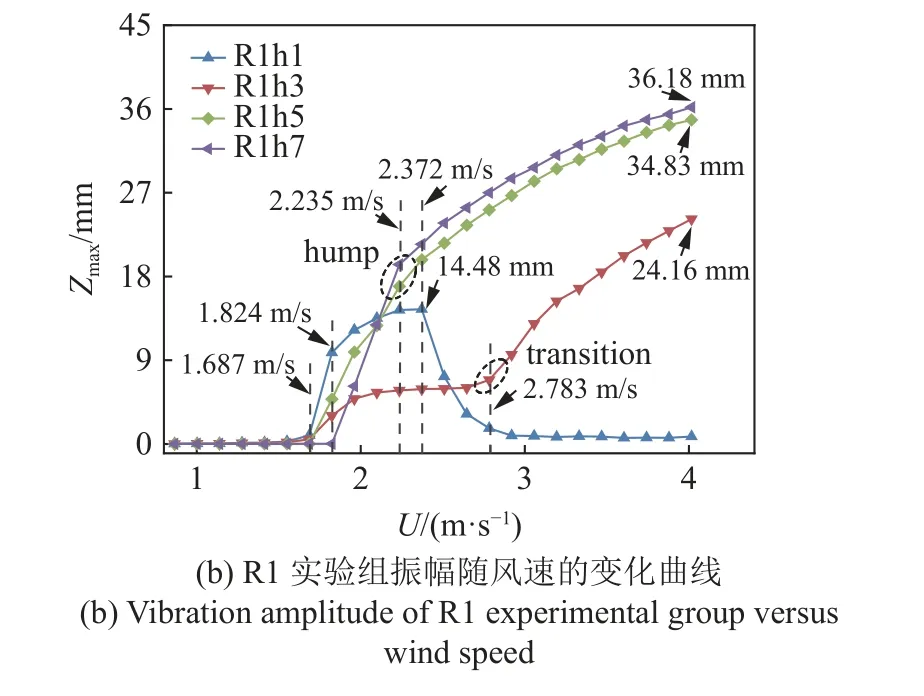
图10 R1 实验组风洞实验结果Fig.10 Wind tunnel test results of R1 experimental group

如图10 所示,对于R1 实验组,R1h1 钝体的工作带宽有所缩小,为1.687～2.783 m/s,U=2.372 m/s 时出现最大RMS 电压为3.22 V,与圆柱相比提升了8.78%,与方柱相比降低了53.20%,最大振幅为14.48 mm,与圆柱相比提升了5.00%,与方柱相比降低了58.31%.R1h5,R1h7 钝体则与涡激振动完全不同,其特性与方柱类似,但与经典驰振又有所区别.其中R1h5,R1h7 均在U=2.235 m/s 处出现 ‘驼峰’ 现象,导致其RMS 电压与振幅的增长率逐渐降低.最终,R1h5 的起振风速为1.687 m/s,最大RMS 电压为7.07 V,与圆柱相比提高了138.85%,与方柱相比则提升了2.76%,最大振幅为34.83 mm,与圆柱相比提升了152.57%,与方柱相比则提升了0.29%.R1h7 的起振风速为1.824 m/s,最大RMS 电压为7.23 V,与圆柱相比提升了144.26%,而与方柱相比则提升了5.09%,最大振幅为36.18 mm,与圆柱相比提升了162.36%,而与方柱相比则提升了4.18%.

R1 h3 则处于从涡激振动向驰振的过渡阶段,其在U=1.687～2.783 m/s 为较缓和的涡激振动,在U>2.783 m/s 后基本转为驰振.其最大RMS 电压为5.20 V,与圆柱相比提升了75.68%,与方柱相比降低了24.42%,最大振幅为24.16 mm,与圆柱相比提升了75.20%,与方柱相比降低了30.44%.

如图11 所示,对于R2 实验组,R2h1 的工作带宽轻微缩小,为1.550～2.920 m/s,U=2.372 m/s 时达到最大RMS 电压为2.86 V,与圆柱相比降低了3.38%,与方柱相比降低了58.43%,最大振幅为13.59 mm,与圆柱相比降低了1.45%,与方柱相比降低了60.87%.R2h3,R2h5,R2h7 特性则与方柱类似,起振风速分别为1.550 m/s,1.687 m/s,1.824 m/s,最大RMS 电压分别为6.92 V,6.60 V,6.96 V,与圆柱相比,分别提升了133.78%,122.97%,135.13%,与方柱相比,R2h3 提升了0.58%,R2h5 降低了4.07%,R2h7 升高了1.16%,最大振幅分别为35.02 mm,33.22 mm,35.88 mm,与圆柱相比,分别提升了153.95%,140.90%,160.19%,与方柱相比,R2h3 提升了0.83%,R2h5 降低了4.35%,R2h7 升高了3.31%.

图11 R2 实验组风洞实验结果Fig.11 Wind tunnel test results of R2 experimental group

如图12 所示,对于R3 实验组,R3h1 的俘能特性剧烈下降,工作带宽严重缩小,为1.550～2.235 m/s,U=1.961 m/s 时达到最大RMS 电压为0.92 V,与圆柱相比降低了68.92%,与方柱相比降低了86.63%,最大振幅为3.99 mm,与圆柱相比降低了71.07%,与方柱相比降低了88.51%.而R3h5 尽管其在U=3.057 m/s 后出现 “驼峰” 现象,其RMS 电压增长率在3.194～3.605 m/s 后明显降低,但其依然拥有较好的俘能特性,其最大RMS 电压为10.00 V,与圆柱相比提高了237.84%,与方柱相比提升了45.35%,最大振幅为46.45 mm,与圆柱相比提升了236.84%,与方柱相比则提升了33.74%.R3h7 特性则与方柱类似,起振风速为1.961 m/s,最大RMS 电压为8.40 V,与圆柱相比提高了183.78%,与方柱相比提升了22.09%,最大振幅为42.46 mm,与圆柱相比提升了207.90%,与方柱相比提升了22.25%.

图12 R3 实验组风洞实验结果Fig.12 Wind tunnel test results of R3 experimental group

R3h3 特性则与R1h3 类似,处于从涡激振动向驰振的过渡阶段,其在U=1.687～3.057 m/s 表现为微弱的涡激振动,在U>3.057 m/s 后转为驰振.其最大RMS 电压为4.49 V,与圆柱相比提升了51.69%,与方柱相比降低了34.74%,最大振幅为21.46 mm,与圆柱相比提升了55.62%,与方柱相比降低了38.21%.

如图13 所示,对于R4 实验组,R4h1 的俘能特性依然剧烈下降,工作带宽大幅缩小,为1.687～2.509 m/s,U=1.961 m/s 时达到最大RMS 电压为1.63 V,与圆柱相比降低了44.93%,与方柱相比降低了76.31%,最大振幅为7.41 mm,与圆柱相比降低了46.26%,与方柱相比降低了78.66%.R4h3,R4h5,R4h7 特性则与方柱类似,起振风速分别为1.687 m/s,1.687 m/s,1.824 m/s,最大RMS 电压分别为6.62 V,6.73 V,6.03 V,与圆柱相比,分别提升了123.65%,127.37%,103.72%.与方柱相比,则分别降低了3.78%,2.18%,12.36%,最大振幅分别为32.09 mm,33.68 mm,29.32 mm,与圆柱相比,分别提升了132.71%,144.24%,112.62%,与方柱相比,则分别降低了7.60%,3.02%,15.58%.

图13 R4 实验组风洞实验结果Fig.13 Wind tunnel test results of R4 experimental group

图14 为方柱和R3h5 的位移和电压随风速U的分岔图.其中,位移和电压分别取稳定振动时间段内振动位移和输出电压的幅值.一般来讲,俘能器的基本参数和风速决定了其振动的发生.从图14 可以看出,当风速超过1.687 m/s 时,俘能器开始分岔,出现周期性振动并发生极限环振荡(limit cycle oscillation,LCO).在风速允许的范围内,这种振荡对俘能器来说一般是安全的,因为其振幅恒定,周期恒定,稳定性高.与方柱相比,R3h5 在起振后拥有较大的输出电压,有利于在较低的风速下俘获更多的能量.

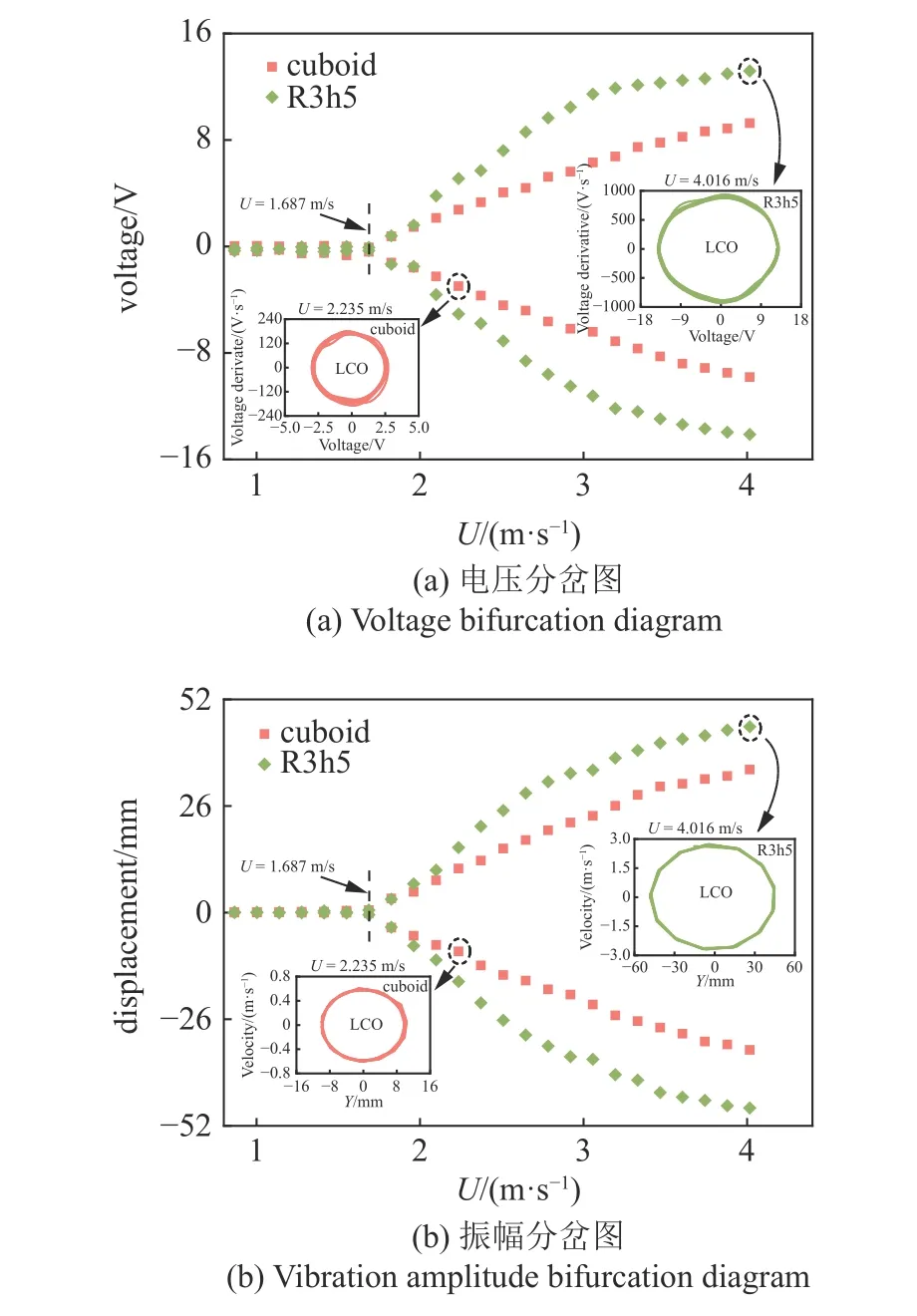
图14 部分钝体振幅与电压随风速的分岔图Fig.14 Bifurcation diagram of vibration amplitude and voltage of various bluff body versus wind speed

3.2 理论模型验证与分析

为验证理论模型的正确性,如表2 所示,通过式(15)～式(18)可计算出压电俘能器的等效参数.为避免重复,选择R3 实验组进行理论模型验证.

表2 压电俘能器的等效参数Table 2 Equivalent parameters of piezoelectric energy harvester

图15～图16 给出了R3 实验组在风速U=2.372 m/s 下的气动力参数识别结果,使用最小二乘法对基于CFD 模拟得到的气动力参数进行非线性曲线拟合可以得到驰振气动力系数Ai.

图15 圆柱与R3h1 的气动力参数识别Fig.15 Aerodynamic coefficient identification of cylinder and R3h1

图16 4 组钝体的气动力系数拟合Fig.16 Aerodynamic coefficient fitting of four bluff bodies

表3 列出了对照组与R3 实验组详细的气动力系数,CFD 模拟得到的数据点基本分布在拟合曲线的两侧,将这些系数代入式(20)～式(22)可得到压电俘能器电压响应的理论结果.如图17 所示,可以看出,理论结果能够基本预测压电俘能器的电压响应.同时也应注意到实验与理论之间的部分误差,这些误差可能来自以下方面: 第1 是实验操作过程中的不确定因素会使压电俘能器的俘能特性存在少量偏离,第2 是CFD 模拟结果通常不会绝对准确,与实际情况相比往往存在误差.

表3 对照组与R3 实验组的气动力系数Table 3 Aerodynamic coefficients of control group and R3 experimental group

对于仅发生驰振的钝体来说,涡驰耦合系数f=0,这使得涡激振动激励项-χfq(τ)(η/Sn)2=0,使得式(21)失效,钝体振动行为完全由驰振力系数Ai决定.其中,A1决定驰振的起振风速,较大的A1能够使式(20)中的驰振阻尼项2ζ+χ(f-A1)η/Sn更早变负,使得钝体在较低风速下出现驰振特性,从而在更宽的风速范围内俘能.而A3,A5,A7则控制式(20)右端的高阶阻尼项,因此较大的A3,A5,A7有助于提升钝体的振幅,从而产生更高的输出电压,而由于A5,A7控制较高阶的阻尼项,其对压电俘能器产生的提升效果并不明显.因此,钝体的输出电压主要由较低阶的气动力系数A3控制.如表3 所示,与方柱对照组相比,R3h7 有较低的A1,因此R3h7 的起振风速较大,而R3h7 有较大的A3,因此R3h7 在高风速区域有较高的输出电压.

对于仅出现涡激振动的钝体来说,斯特劳哈尔数St是控制钝体涡激振动行为的一个关键系数,较高的St可以使钝体更早进入涡激振动的锁定区[30],与圆柱相比,R3h1 的St较小,这也决定了其进入涡激振动锁定区时的风速要高.另一个关键系数为涡驰耦合系数f,当钝体仅出现涡激振动行为时,其驰振力系数Ai=0,涡驰耦合系数f≠ 0,式(20)的驰振阻尼项2ζ+χ(f-A1)η/Sn将退化为涡激振动阻尼项2ζ+χfη/Sn,钝体的涡激振动行为主要由涡激振动阻尼项2ζ+χfη/Sn,尾流振子阻尼项-2βη(1-4f2q2(τ)/)与涡激振动激励项-χfq(τ)(η/Sn)2三者联合控制.当f增大时,涡激振动激励项-χfq(τ)(η/Sn)2的强度增强,钝体从而能够在更宽的风速区间内产生更高的输出电压.尽管涡激振动阻尼项2ζ+χfη/Sn与尾流振子阻尼项-2βη(1-4f2q2(τ)/)也在增大,但阻尼项仅对钝体涡激振动的振幅有一定影响.随着f的增大,钝体涡激振动的电压幅值向高风速区域移动,这也使得钝体涡激振动的带宽显著扩大,而钝体输出电压的增长率则有所降低.

对于既出现涡激振动又出现驰振的钝体来说,此时钝体处于涡驰耦合的状态,涡驰耦合系数f与斯特劳哈尔数St是控制涡驰耦合行为的关键参数.当f≠ 0 时,钝体会出现涡激振动的特征,f的出现影响到了式(20)中的驰振阻尼项2ζ+χ(f-A1)η/Sn和涡激振动激励项-χfq(τ)(η/Sn)2以及式(21)中的尾流振子阻尼项-2βη(1-4f2q2(τ)/).增大f同样使得以上三者同时增大,若钝体在低风速区域已经出现驰振,f的增大降低了驰振阻尼项2ζ+χ(f-A1)η/Sn中负阻尼的绝对值,导致钝体在低风速区域的输出电压降低,同时涡激振动激励项-χfq(τ)(η/Sn)2在逐渐增大,则平衡了负阻尼绝对值减小带来的输出电压降低现象.而St≠ 0 使得钝体在某一风速后出现了涡激振动特征,导致电压增长率降低,从而使RMS电压曲线在部分风速区域内变得平稳,这也是出现“驼峰” 现象的主要原因.对R3h5 来说,较低的St使得其在高风速区域内出现涡激振动特征,RMS 电压增长率明显变缓.与方柱相比,尽管R3h5 有较高的A1,但较大的f使得其起振风速没有明显降低,与其余钝体相比,R3h5 有最高的A3,这使得其存在最高的输出电压.若钝体仅在高风速区域出现驰振,比如R3h3,此时在一定风速范围内,钝体涡激振动与驰振特征是分开的,则f与St主要控制低风速区域内涡激振动的特性,与圆柱和R3h1 相比,R3h3 拥有更小的St,这使得其进入涡激振动锁定区的风速继续增大,而其最小的f值使得其在出现驰振特征前存在微弱的涡激振动特征.

3.3 不同接口电路对俘能器性能的影响

接口电路是俘能器的重要组成部分,能够将压电俘能器输出的交流电转化为可以直接利用的直流电,对提升俘能器的能量转化效率以及电路负载适应性等方面具有关键作用.

图18 展示了标准直流 (DC)接口电路,该电路由一个全波整流桥 (full-wave rectifier,FWR)和一个滤波电容C1组成,全波整流桥由4 个型号相同的二极管组成,RL为外接负载,元件参数与型号见表4.

图18 标准直流接口电路Fig.18 Standard DC interface circuit

输入端一般为来自压电俘能器的交流信号,对于每个正电压周期,总有一个二极管正向导通,因此,输出电压是整个周期的正半周期.对于每个负电压周期,与前一个周期相同的二极管将反向截止,而另一个二极管则正向导通,此时输出电压是整个周期的负半周期,但对于负载来说,电流方向没有发生改变.滤波电容C1则用于滤除电路中交流干扰信号,使输出端的直流电信号更加平滑.

图19 展示了自供能同步电荷提取接口电路 (selfpowered synchronous charge extraction circuit,SPSCE),该电路由一个全波整流桥,一个同步开关(synchronous switch,SS)和一个反激式转换器(flyback converter,FC)组成,元件参数与型号见表4.

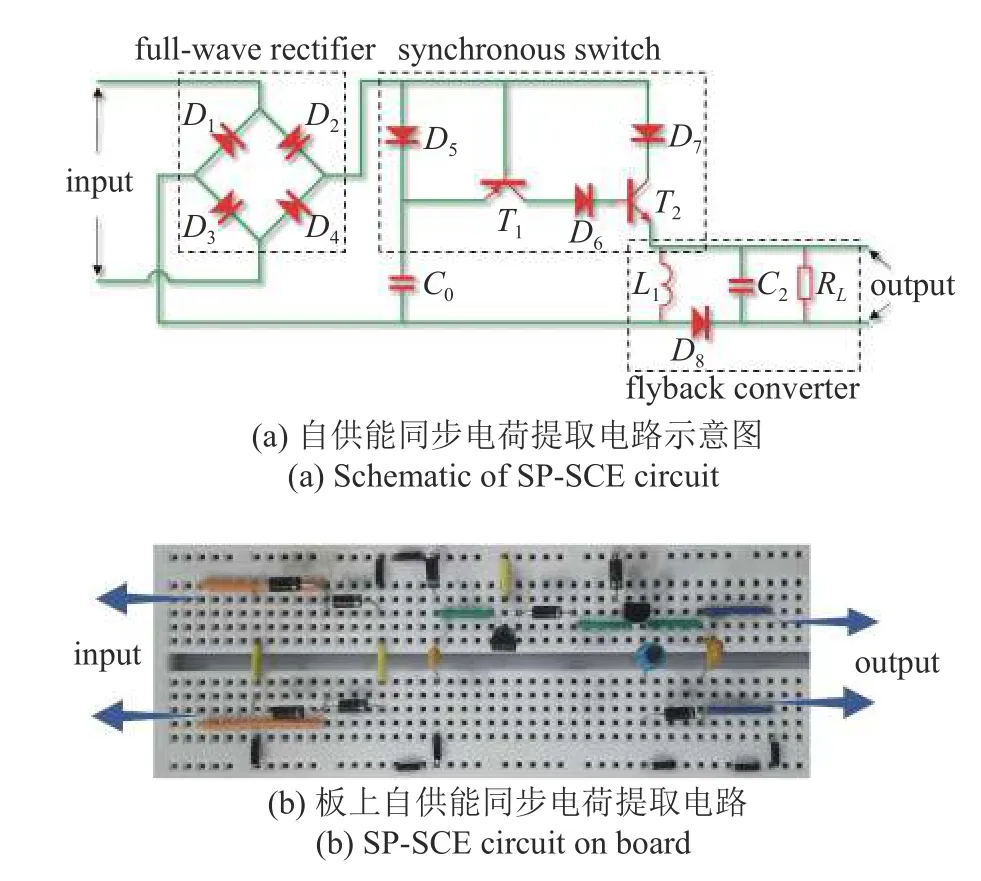
图19 自供能同步电荷提取接口电路Fig.19 Self-powered synchronous charge extraction (SP-SCE)interface circuit

输入端信号在经过全波整流桥整流后首先给电容C0充电,此时二极管T1和T2断开,C0两端电压不断上升,当输入端电压达到峰值时,下一时刻输入端电压下降,C0向外电路放电,T1与T2导通,将输入端的部分能量转移并储存在电感L1中,直到C0两端电压小于输入电压时,电路继续给电容C0充电,T1,T2截至,电感L1产生的感应电流通过二极管D8整流和电容C2滤波后,在输出端RL处得到稳定的直流输出.

选择R3h5 实验组,在U=2.783 m/s 及U=3.742 m/s 条件下,研究不同接口电路对俘能器输出特性的影响.图20 为在给定条件下,PZT-5 两端(接口电路输入端)与输出端RMS 电压随负载电阻的变化情况.图20(a)为在两个不同的风速以及不同接口电路的条件下PZT-5 两端RMS 电压随负载的变化情况,可以看出,在DC 电路的条件下,PZT-5 两端RMS 电压随RL的增大而增大,而在SP-SCE 电路的条件下,随着RL的增大,PZT-5 两端的RMS 电压却较为恒定.图20(b)为在不同接口电路的情况下,输出端的RMS 电压值随负载RL的变化曲线,可以看出,在不同接口电路的条件下,输出端的RMS 电压都随RL的增大而增大.

从电学角度来看,振动过程中压电片可以简化为一个正弦电流源与其夹持电容Cp并联的等效电路.在标准DC 接口电路中,电路的总阻抗可以看成负载电阻RL,夹持电容Cp,滤波电容C1三者结合的等效阻抗,由于Cp与C1值很小,两者的容抗占电路总阻抗的比例可以忽略不计,电路电压完全取决于RL.因此,RL越大,PZT-5 两端电压越大,RL两端电压也越大.在SP-SCE 接口电路中,同步开关仅将输入端的部分能量转移并储存在L1中,最后通过反激式转换器释放到RL上,此时L1,C2,RL,D8构成一个独立的回路,RL与输入端基本不相关.因此,在SPSCE 电路中,PZT-5 两端电压基本不随RL变化.

消耗在RL上的平均功率Pave可以由以下公式计算

如图21 所示,在U=2.783 m/s 条件下,RL<0.4 MΩ 时,标准DC 电路中Pave基本大于SPSCE 中的Pave,而在RL>0.4 MΩ 后,SP-SCE 电路中的Pave则大于DC 电路中的Pave.当RL=1.5 MΩ 时,SP-SCE 电路的Pave=9.61 μW,标准DC 电路的Pave=7.90 μW,此时SP-SCE 电路的Pave比DC 电路高21.65%左右.

图21 不同接口电路条件下负载的输出功率Fig.21 The output power of the load resistance under different interface circuit conditions

在U=3.742 m/s 时,在RL<0.8 MΩ 时,标准DC 电路中Pave基本大于SP-SCE 中的Pave,而在RL>0.8 MΩ 后,SP-SCE 电路中的Pave则大于DC 电路中的Pave.当RL=2.0 MΩ 时,SP-SCE 电路中的Pave=15.51 μW,标准DC 电路中的Pave=13.94 μW,此时SP-SCE 电路的Pave比标准DC 电路高11.26%左右.且在两个风速条件下,随着RL的增大,SP-SCE 电路的输出功率逐渐比标准DC 电路稳定,这是因为在SP-SCE 电路中,RL消耗了储存在L1中的能量,而这一部分能量一般是固定的,且由左侧的输入端决定.而在标准DC 电路中,整个电路的等效阻抗随负载RL的变化而变化,从而导致消耗在RL上的能量也在变化.因此,标准DC 电路对负载RL的变化比较敏感,需要为标准DC 电路匹配合适的RL以保证获得稳定的功率输出,而在SP-SCE 电路中,不需要过多地为电路做阻抗匹配.

3.4 基于CFD 的流场分析

图22(a)～图22(b)显示了在U=1.687 m/s 时圆柱与R3h1 实验与3D CFD 模拟的位移时程曲线.可以发现,3D CFD 位移曲线基本与实验相似.为了说明翅片超表面对流场的影响,图22(c)显示了两者在一个振动周期内的旋涡脱落过程,可以看出两者的涡量云图则都显示出经典的 “2S” 模式,光滑圆柱后方的旋涡强度更强,较强的旋涡会在钝体上下表面产生较大的压力差,从而引发钝体更明显的振动来提高俘能性能,而R3h1 后方的旋涡强度相对较弱,这使得R3h1 上下表面压力差较小,使得振动幅值降低从而导致俘能性能降低.

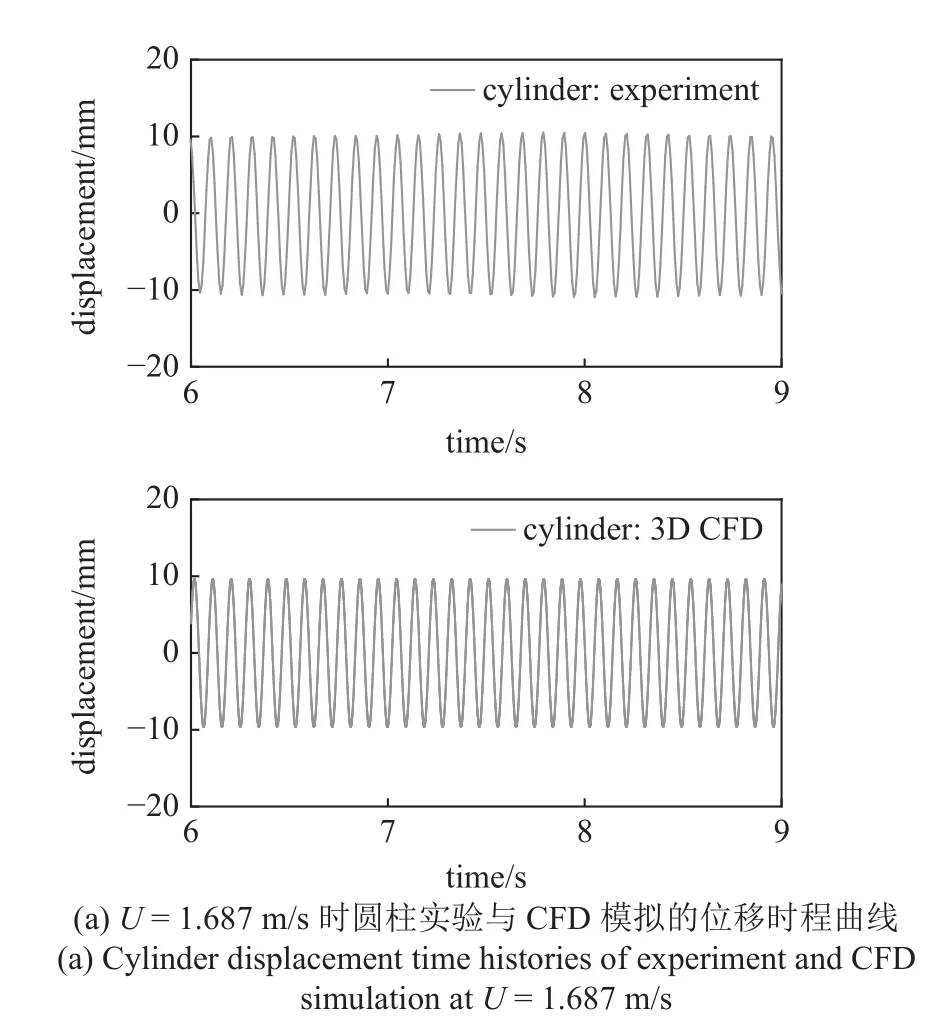
图22 U=1.687 m/s 时圆柱和R3h1 的位移时程曲线与涡量云图Fig.22 Displacement time histories and vorticity contours of cylinder and R3h1 at U=1.687 m/s

图23(a)～图23(b)显示了在U=2.509 m/s 时方柱与R3h5 实验与3D CFD 模拟的位移时程曲线.同样地,图23(c)显示了两者在一个振动周期内的旋涡脱落过程,可以看出两者的涡量云图差别较大,R3h5 显示出较强的 “2S” 模式,而方柱则由于尖角的存在使得流体的状态在尖角处发生急剧变化,导致流动紊乱,迫使流体提前脱离壁面[38-39]而形成紊流旋涡,气动力系数随攻角α增大而减小从而出现负斜率,从而使得方柱易于出现驰振.R3h5 较高的翅片超表面使其具有一定的尖角结构,翅片会在尖角处引起局部湍流,使流动提前分离,且其不对称的几何结构导致其升力系数出现负斜率从而出现驰振,但R3h5 本身的圆柱特征又使其在旋涡脱落过程中具有一定的规律性,这也是其在高风速下出现涡激振动特征的原因.与方柱相比,普通圆柱的弧形表面有利于减小流动阻力,且圆柱的轴对称特征也有助于维持流动的稳定性.但这对俘能来说却是不利的.

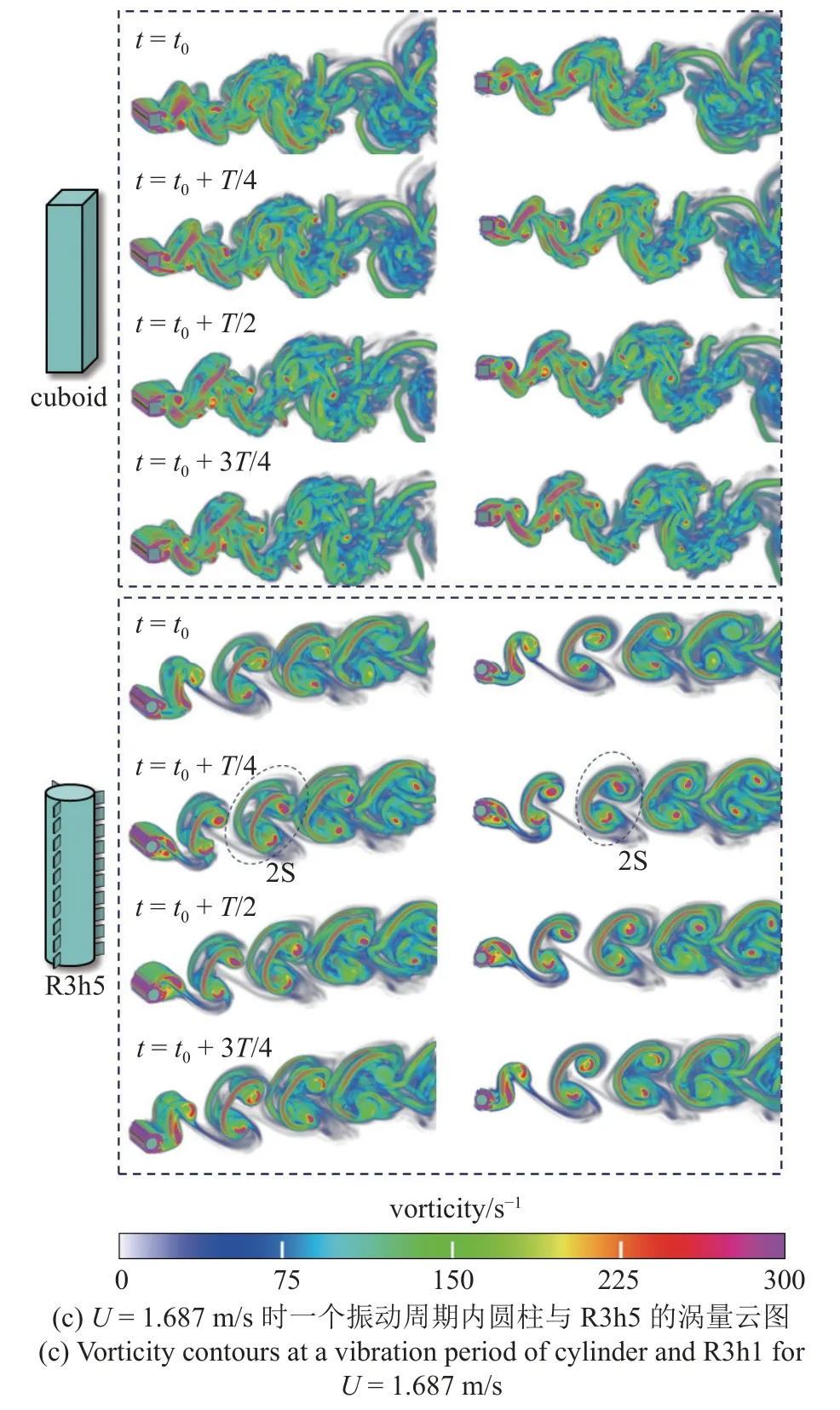
图23 U=2.509 m/s 时方柱和R3h5 的位移时程曲线与涡量云图Fig.23 Displacement time histories and vorticity contours of cuboid and R3h5 at U=2.509 m/s

4 结论

本文在圆柱表面添加翅片超表面结构成功实现了钝体振动的抑制以及钝体振动特性从涡激振动向驰振的转变.基于Tamura-Shimada 模型,推导了SDOF 压电俘能器流-固-电耦合理论模型,并通过风洞实验验证了理论模型的准确性,同时也发现不同高度和数量的翅片超表面结构能够显著改变俘能器的气动力参数从而对俘能性能有较大影响,这是影响俘能器俘能性能的重要原因.通过风洞实验可知,R3h1 的振幅仅有3.99 mm,与普通圆柱相比,降低了88.51%.尽管R3h5 在高风速下出现了涡激振动特征,但其Vrms高达10.00 V,比圆柱高236.84%.当风速超过相应驰振起振风速时,压电俘能器出现驰振特征,并表现为 稳定的LCO.而通过CFD 仿真可知,与圆柱相比,R3h1 后方的旋涡强度明显较弱,因此抑制了其涡激振动.与方柱相比,R3h5 特殊的尖角结构与圆柱曲面使其出现驰振特征后仍保持了旋涡结构的稳定性.而通过给俘能器接入SP-SCE电路则进一步提升了其俘能性能,在实验测试范围内,SP-SCE 电路比标准DC 电路最大可提升21.65%的输出功率,且随着RL的增加,SP-SCE 的功率输出比标准DC 电路更稳定.这为高性能压电俘能器的设计和优化提供了重要的研究基础.