Sliding mode-based adaptive tube model predictive control for robotic manipulators with model uncertainty and state constraints

Erlong Kang·Yang Liu·Hong Qiao

Abstract In this paper,the optimal tracking control for robotic manipulators with state constraints and uncertain dynamics is investigated,and a sliding mode-based adaptive tube model predictive control method is proposed.First, utilizing the high-order fully actuated system approach, the nominal model of the robotic manipulator is constructed as the predictive model.Based on the nominal model, a nominal model predictive controller with the sliding mode is designed, which relaxes the terminal constraints,and realizes the accurate and stable tracking of the desired trajectory by the nominal system.Then,an auxiliary controller based on the node-adaptive neural networks is constructed to dynamically compensate nonlinear uncertain dynamics of the robotic manipulator.Furthermore,the estimation deviation between the nominal and actual states is limited to the tube invariant sets.At the same time,the recursive feasibility of nominal model predictive control is verified,and the ultimately uniformly boundedness of all variables is proved according to the Lyapunov theorem.Finally, experiments show that the robotic manipulator can achieve fast and efficient trajectory tracking under the action of the proposed method.

Keywords Tube-based model predictive control·Robotic manipulator·Sliding mode·Node-adaptive neural networks·Model uncertainty

1 Introduction

In past few decades,robotic manipulators have been widely studied and applied in both industry and academia,moreover,its control design and analysis have received extensive concern.One of the important issues to be investigated in robotic control is to overcome the influence of complex uncertain dynamics.Robust control [1, 2] and adaptive control [3, 4]are two common theoretical frameworks used to deal with this problem.In recent years,the realization of optimal control performance is paid more and more attention, and it has become another significant issue in robotic controller design.Researchersadopttheslidingmodecontroltoachieve wanted control performance such as fast transient response[5]and high control precision[6].Optimal control[7,8]is also utilized for improving the control performance of robots.Overall,achieving optimal control for actual robotic manipulators with the limitation of complex uncertain dynamics is still a continuous hotspot that has attracted much attention.

Model predictive control (MPC) is well known for efficiently and powerfully solving the optimal control problem of constrained and multivariable systems[9,10].However,MPC is one of the typical model-based methods,an explicit predictive model is usually necessary [11].It is challenging to use MPC to handle uncertain systems such as robotic manipulators.

One common scheme to overcome the above challenge is to build suitable predictive models by learning.Researchers propose the neural networks (NNs) model [12–14], fuzzy systems model [15], Gaussian process model [16], recurrent fuzzy NN model [17], etc.for different systems.As a whole, both offline learning models [12, 13, 15, 16] and online learning models[14,17]have been investigated and adopted.However,for the offline learning model,the uncertainty of the system dynamics cannot be dealt with in real time;for the online learning model,the predictive model is updated in real time,which may increase the computational complexity of the optimization problem of MPC.

Another alternative thought for this challenge is to design an effective feedback correction method, which compensates for the uncertainty of the robotic manipulator.This idea can avoid introducing the complex uncertain model into the solving of the optimization problem, therefore, the computational complexity of the MPC is simplified.Tube-based MPC is an effective method to achieve this target.In[18],a robust tube MPC is developed for tracking control of robotic manipulators with disturbances.In [19], a fast tube MPC scheme is used to the moving tracking control of a redundant underwater vehicle-manipulator system,and the unmodeled uncertainties are treated in the form of disturbances.The tube-based MPC scheme is also used in the control of linear parameter varying(LPV)systems[20],nonlinear time-delay systems [10], etc.However, most previous research has focused on systems that look like ˙x=f(x,u)+w,in which ˙x=f(x,u)is the nominal model,wis the disturbances or equivalent external disturbances.For the unknown robotic system, realizing the dynamic compensation of the uncertain nonlinear model under the tube-based MPC scheme is still difficult.How to construct a proper nominal model,and design the corresponding auxiliary controller remains to be further investigated.

The other important and challenging problem for MPC is the design of the objective function.It not only affects the realization of the optimal control performance of the system,but also plays an important role in the stability analysis of the controller.MPC with terminal cost function and terminal constraints is a widely used method for constructing the objective function [21, 22].However, most theoretical research on this category has focused on the stability analysis[14,23,24],and there is relatively less discussion about the optimality index.Furthermore, the introduction of terminal constraints means that it is complex to analyze the stability of the system and design the related parameters.For example,researchers present contractive terminal constraints[25],time-varying terminal constraints[26],etc.for stability analysis of MPC.Therefore, developing an effective objective function of MPC, which can relax the terminal constraints,simplify the parameter design, and ensure the control performance and stability of the system, is an issue deserving research.

One approach for solving the above problem is to introduce a sliding mode into the objective function of MPC.On one hand, sliding mode control (SMC) is one of efficient robust control methods,which can achieve high control precision[6].On the other hand,under the control of SMC,the system state can converge along the defined sliding mode surface, which can be regarded as the state constraint.The combination of MPC and SMC for nonlinear system control has been studied, but most research focuses on the following two aspects.(1)MPC is utilized for solving the auxiliary controller of SMC, so that the system state can converge to the sliding mode surface in an optimal way [27].Then,the chattering phenomenons of SMC can be improved.(2)The optimal controller of the nominal system is solved by MPC,and the SMC is used to estimate and compensate for the uncertainties or disturbances of the actual system [28,29].As far as we know,there is less previous research which introduces the sliding mode into the design of the objective function of MPC.

In order to solve the problems discussed above,a sliding mode-based adaptive tube MPC (SM-ATMPC) strategy is proposed for uncertain robotic manipulators with state constraints.The main contributions are summarized as follows:

(1) For the nominal MPC, the predictive model of the robotic manipulator is developed based on the high-order fully actuated (HOFA) system approach, and the objective function is designed by introducing the sliding mode,which is constructed by the nominal tracking error and defined virtual states.Besides, the nominal state constraints are transformed into input constraints by solving the dynamic differential equations.Then, the terminal constraints are relaxed,and the accurate and stable tracking of desired trajectories by the nominal system is achieved.

(2) The auxiliary controller for the tube MPC is constructed based on the node-adaptive NNs.The adaptive adjustment method for the neural nodes of NNs and the adaptive updating laws of NNs’weights are developed.The nonlinear uncertain system model of the robotic manipulator is dynamically compensated by the NNs,and the estimated deviation between the nominal and actual states is limited to the tube invariant set.

(3) The recursive feasibility of the nominal MPC is verified.The stability of the closed-loop system is proved according to the Lyapunov theorem,and all variables satisfy the ultimately uniformly boundedness(UUB).Furthermore,the effectiveness of the proposed control method is verified by hardware experiments.

The remainder of this paper is organized as follows.In Sect.2,related basic methods and lemmas are introduced,the dynamics of the robotic manipulator and its tracking control problem are described.Section3 presents the definition of the nominal system for the robotic manipulator, the design of the nominal MPC strategy and the auxiliary controller,as well as the stability analysis of the closed-loop system.In Sect.4,the performance of the presented control method is illustrated by comparative experiments.Section5 concludes this paper.

2 Preliminaries and problem formulation

2.1 High-order fully actuated system approach

The HOFA system is a kind of control-oriented model and approach proposed by Duan [30].For a nonlinear system with the following form:

wherex∈Rnis the system state,u∈Rris the control input,f(·,·) ∈Rnandg(·,·) ∈Rn×rare sufficiently differentiable vector and matrix functions, respectively.E∈Rn×nis a constant matrix,θ fandθgare state-independent parameter vectors.If rankgholds for allt>0 under given conditions,the system(1)is seen as fully actuated.Then,the controller can be constructed as

whereAi∈Rn×n,i=1,2,...,m-1 are given coefficient matrices,visthecontrollerforthetransformedsystem.Based on the designed controller(2),the nonlinear system(1)can be transformed into the following linear closed-loop system:

The expected performance of system(3)can be obtained due to the arbitrariness ofAi,i=1,2,...,m-1[30,31].

2.2 Lemma and problem formulation

The tracking control problem of uncertain robotic manipulators with state constraints is considered.The dynamics model of a rigid robotic manipulator is formulated as follows[18]:

in whichq, ˙qand ¨q∈Rnrepresent the joint position,velocity and acceleration,respectively.M(q)∈Rn×nis the symmetric and positive definite inertia matrix,C(q, ˙q) ˙q∈RnandG(q)∈Rnrepresent the centripetal and Coriolis force,and the gravitational force.τ∈Rnrepresents the input torque.Generally, the joint position and velocity of the robotic manipulator are subject to constraints as follows:

The control objective is to construct a suitable model predictive controller which can drive the robotic manipulator trackingthedesiredtrajectoryqd(t)=[qd1(t),qd2(t),...,qdn(t)]Tunder the limitation of model uncertainty and state constraints.

3 Main results

3.1 Construction of the predictive model

The robotic manipulator(4)is one of the typical second-order fully actuated systems [31].Therefore, the HOFA system approach can be utilized to construct the nominal model of the robotic manipulator as the predictive model.The nominal model is defined as follows:

3.2 Sliding-mode-based nominal model predictive controller

In this part,a sliding-mode-based nominal MPC controller is constructed to make the nominal tracking error ¯econverge to a neighborhood of zero.For convenience,the nominal model(6)is re-expressed as a state-space model:

For relaxing the terminal constraint and omitting its offline design, first, the nominal state constraints are transformed into the nominal input constraints according to the solution of the differential equation(8).The solution is expressed as follows[32]:

In order to facilitate expression and analysis,the optimal solutions obtained by solving the optimization problem of MPC at timetkare denoted as(·)∗(t|tk);the feasible solutions att∈[tk,tk+T)for MPC is denoted as(·)∧(t|tk).

Next,the terminal controller is considered.For the nominal system(8),letτ fmpc represent a terminal controller.Then,,the following conditions are satisfied:

Therefore,the terminal controller(19)satisfies conditions of formulas(17)and(18).

The following theorem illustrates that the nominal tracking error ¯eis UUB under the action of the nominal MPC controller.

and therefore,the nominal tracking error ¯eremains UUB.■

Remark 1The virtual stateϑis introduced for constructing the terminal controller.It is worth noting that in practical applications, the optimal controllerobtained by the nominal MPC strategy(15)and(16)always satisfies the input constraints, which meansΔτ= 0n×1.Furthermore, it can be obtained thatϑ= 02n×1is satisfied in the whole control period.Therefore,the nominal tracking error ¯ehas the same convergence with ˇe.Then,the actual tracking erroredepends on the deviation between the nominal and actual statesxe.

3.3 Auxiliary controller with node-adaptive neural networks

In this part,the auxiliary controller is designed to make the deviation between the nominal and actual statesxeconverge.According to the HOFA approach, the ideal auxiliary controller can be constructed as follows:

wheref(q, ˙q)=C(q, ˙q) ˙q+G(q).

Then,∀t∈tk,tk+1),the tube-based MPC controller can be designed as

Substituting (27) into (4), we havexe= 02n×1.However, the auxiliary controller (26) might be unprocurable because of the uncertainties existing inf(q, ˙q)andM(q).To overcome these challenges, the auxiliary controller ˜τis redesigned based on node-adaptive NNs.

To confirm the constraintxe∈Ωxeis satisfied in the whole motionperiod,inspiredbytheworkof Zhao[34],Zhang[35],etc., an artanh-type nonlinear transformation is introduced for mapping the constrained statexeto a new unconstrained stateχ.Definethen the artanh-type nonlinear transformation is designed as

The inverse transformation can be calculated by

It is obvious that the initial statexe(0) = 02n×1∈Ωxe.Then,the following Lemmas can be given according to(28)and(29).

Lemmas 2 and 3 show that the objective of making the deviation between the nominal and actual statesxeremain within an invariant set and converge to the domain of zero can boil down to makingχremains UUB.

For designing an appropriate auxiliary controller,first,the dynamics model ofχis calculated as follows:

Then,the auxiliary controller is constructed through backstepping method[34,36].

Step 1:the coordinate transformation is defined as

whereα1is the virtual controller which will be designed latter.

Step 2:Define the Lyapunov function candidate asVχ1=.Its time derivative is

The pseudo-inverse transformation can be rewritten in compact form as

whereβ2=diag(β21,β22,...,β2n)is symmetric and positive definite in the compact setΩxe.

Substituting(33)and(35)into(34),it can be obtained that

where ˆa1=a1β2is symmetric and positive definite in the compact setΩxe.Young’s inequality is employed in (36).The virtual controllerα1is designed as

whereK1is a positive definite symmetric matrix.Substituting(37)into(36),one gets

Substituting(40)into(39),it can be obtained that

where ¯c(πF)represents the average value of centers of Gaussian functions corresponding tom fmiddle layer nodes with the largest output values,o f∈(0,1) is the tunable coefficient.

Hence,the activation output and connection weight of the updated NNs can be represented as

The neural nodes of NNs ˆB(q) have the same adaptive adjustment strategy, which will not be described in detail here.

Step 5: In this part, the auxiliary controller is designed based on node-adaptive NNs constructed in the last step.According to(41),the auxiliary controller is designed as

whereK2is a positive definite symmetric matrix.Substituting(47)into(27),and utilizing ˆB(q)to approximateM(q),one has

Substituting(48)into(41),it can be obtained that

The adaptive laws of ˆW fand ˆWBare constructed as follows:

Inthefollowingtheorem,thetransformedstatesχ1,χ2and the estimation errors of NNs’weights ˜W f, ˜WBare demonstrated to be UUB under the tube-based MPC controller(48)with NNs’learning strategies(50)and(51).

Theorem 2Consider the robotic manipulator(4)controlled by the proposed controller(48).The corresponding nominal

ProofDefine the Lyapunov function candidate as

Substituting(50)into the first term of(53)yields

Similarly,the second term of(53)can be expressed as

whereκB2=θB0ηBΛzχ2.

Substituting(38),(49),(54)and(55)into(53),one has

Next, the boundedness of transformed statesχ1andχ2are interpreted.χ1is obviously UUB sinceχ1=zχ1.Then,according to Lemma 1,the constraintxe1∈Ωxeis satisfied.Consideringγ1and ˙γ1are bounded variables,the virtual controllerα1is UUB.Then, from (33), it can be obtained thatχ2is also UUB.

4 Experimental studies

Fig.2 The xMate7 Pro robotic manipulator

The prediction horizon is selected asT= 0.05s, and the solving interval of the optimization problem is selected asΔt=0.01s.

For the auxiliary controller:functions of the tube invariant setΩxeare chosen asγ1i=γ2i= 3×e(-0.4t)+0.5,i=1,2,3.The control gains of the virtual controllerα1and the auxiliary controller ˜τare selected asK1=diag(1.5,1,1),K2=diag(25,6,10),respectively.According to the definition of time-varying functionsγ1i, ˙γ1and ¨γ1can be represented linearly byγ1.Then, ˆFX+can be seen as the function ofq, ˙q,xe1,xe2andγ11.It is developed with 8 initial middle-layer neurons,and the corresponding centers of Gaussian activation are designed as[-1,1]×[-1,1]×[-1,1]×[-1]×[1]×[0]×[0]×[0]×[0]×[0]×[0]×[0]×[0].The NNs ˆWTBϕB(q)is developed with 2 initial middle-layer neurons, and the corresponding centers of Gaussian activation are designed as[-1.6,1.6]×[0]×[0].The variances are set to be 25.The parameters related to node updating of NNs can be selected asm f0 =6,Φ f=0.8,o f=0.4;m B0 =3,ΦB=0.7,oB=0.2.

Fig.3 Experimental results under the proposed control method

The experimental results are shown in Figs.3 and 4.Figure 3a, b shows the joint position and velocity trajectory,respectively.Figure 3c shows the tracking errors of joint position.These results suggest that constraints of the joint position and velocity are satisfied, and the tracking errors of joint positione1i=qi-qdi,i= 1,2,3 can converge to compact setsΩe1i:= {e1i||e1i|≤0.01} within 2s.Figure 3d expresses the deviationxebetween the nominal and actual states,wherexe1andxe2represent the deviations of the joint position and velocity, respectively.Figure 3e, f shows the comparison between the nominal and actual trajectory,taking joint 4 as an example.Figure3d–f indicates that the estimation deviationxeis guaranteed to be inside the defined tube invariant set.Figure 4 shows the snapshots of the joint trajectory.

For further demonstrating the performance of the proposed sliding mode-based adaptive tube MPC method, the comparison experiments with the PD control, the adaptive neural networks control (ANNC) and the constraint MPC(CMPC)method are considered in this part.

To design the PD controller,the tracking error is first constructed according to the backstepping method[36].Definez1=qd-q,z2=α1- ˙q,in whichα1= ˙qd+K1z1represents the auxiliary controller.The PD controller is designed asτP D=K pz2-z1+Kq˙q,and the control gains are chosen asK1=k1×K1f,k1= 1+3×e-5×‖z1‖,K1f= 2,K p=diag(25,10,18),Kq=diag(18,8,10).

TheANNCcontrollerisdesignedasτN N=-z1+K pz2+ˆWTϕ(zN N).The definitions ofz1andz2are same as those in the PD controller, and the control gains are chosen asK1=diag(1.5,1,1),K p=diag(18,10,8).ˆWTϕ(zN N)is NNs with 64 middle-layer neurons,which is used to estimate theuncertaintermsM(q) ˙α1+C(q, ˙q)α1+G(q).TheNNs’input is selected as,the activation functionϕ(zN N)is the Gaussian function,and corresponding centers are chosen as[-1,1]×[-1,1]×[-1,1]×[0]×[0]×[0]×[-1,1]×[-1,1]×[-1,1]×[0]×[0]×[0],the variance is set to be 25.The update law of weights ˆWis chosen to be the same as(50).

The comparison results are shown in Fig.5 and Table 1.Compared with other three methods, the proposed method has better performance in response speed and tracking precision.The specific analysis and comparison are as follows:

(1)Comparison results with the PD control method

PD control is one of the model-free control methods.To alleviate the influence of the uncertain nonlinear dynamics,the control gainK1is chosen as a state-dependent timevarying parameter.K1is small when the tracking error is large to avoid making the control torque infeasible,andK1increaseswiththedecreaseoftheerror.Furthermore,thejoint velocity is introduced for compensating.However,there still exists obvious steady-state error under the PD controller.

(2)Comparison results with the ANNC method

Both ANNC method and the proposed method adopt adaptive NNs to estimate and compensate the uncertain nonlinear model of the robotic system,therefore,the steady-state errors under these two methods are small.However, the response speed and the tracking precision under the proposed method is better.In addition, the presented method adopts nodeadaptive NNs, in which the final numbers of middle-layer neurons arel f= 18,lB= 2.Compared to the NNs with fixed structure, the node-adaptive NNs have smaller scale and higher real-time performance.

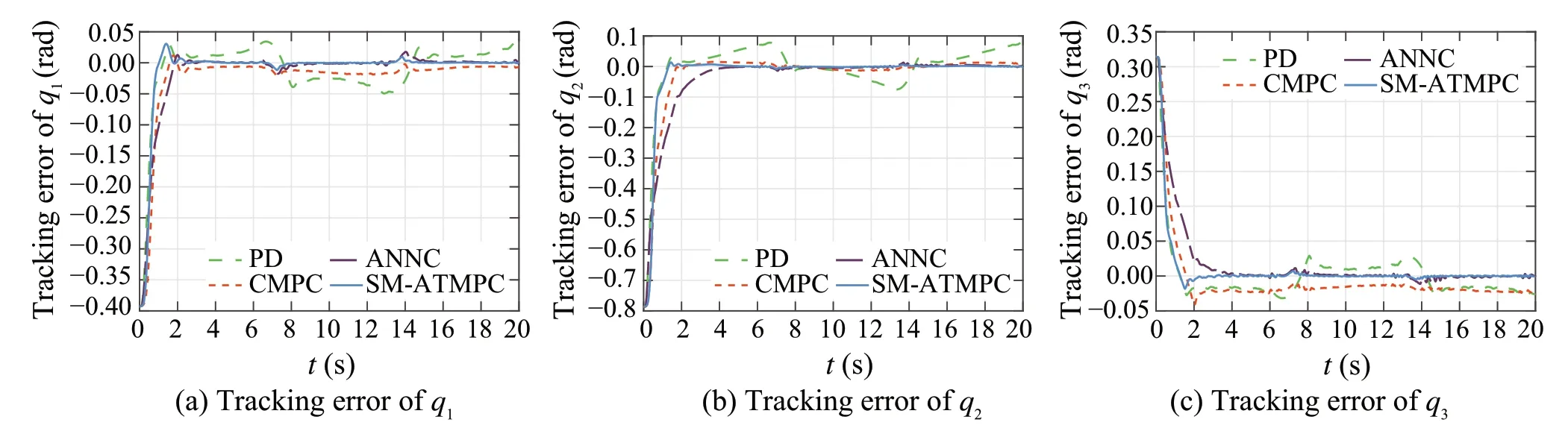
Fig.5 Joint position tracking errors under different control methods

Table 1 Comparison of control performance indexes under different control methods

(shown in Fig.6) illustrate that when the desired trajectory changes, the vibration of control torques obtained by the ANNC method is relatively violent,and the response speed is also slow.The control performance under the proposed method is better.

(3)Comparison results with the CMPC method

It can be found that compared with the proposed nominal MPC strategy by introducing sliding mode, the CMPC method has poor control performance in response speed and tracking precision.Moreover, the stability condition of the proposed nominal MPC strategy is related to the parameter of the terminal controllerksand the parameter of the terminal costP, and its control performance can be adjusted by tuning the parametercof sliding mode.By contrast,the stability condition and control performance of the nominal CMPC method are related to parametersQ,R,QNof the objective function and the prediction horizonT.The parameters need to be designed and calculated offline in advance[42].Furthermore, parameters design for stability analysis and performance adjustment is coupled, changing one of the parameters may affect the overall control performance.Take parametersRandTfor example, ifRis chosen asR2=diag(0.05,0.05,0.05)(corresponding CMPC method is denoted as CMPC-2),the performance of the tracking precision will degrade greatly; ifTis chosen asT2= 0.08s(corresponding CMPC method is denoted as CMPC-3),the performance of tracking precision is improved,but the calculation burden increases.The comparison results are shown in Fig.7.

The above analysis indicates that compared with the nominal CMPC method,the proposed nominal MPC strategy by introducing sliding mode has advantages in ensuring control performance and simplifying design.

Furthermore, two groups of experiments are conducted separately to analyze the robustness of the proposed method against external disturbances and observation errors.(1)Random external disturbances are added, and the results are shown in Fig.8.(2) 2% observation errors of joint position are added, and the results are shown in Fig.9.Figures 8b,9b illustrate that the proposed control method is robust to bounded external disturbances and finite observation errors.

In summary,the sliding mode-based adaptive tube MPC method proposed in this paper can effectively solve the tracking control problem of robotic manipulators with model uncertainty and state constraints.The nominal MPC strategy by introducing sliding mode is presented to achieve highperformance trajectory tracking of the nominal system;and the auxiliary controller with node-adaptive NNs is presented to compensate for the nonlinear uncertain model of robotic manipulators using small-scale NNs.The proposed method is also robust to bounded external disturbances and finite observation errors.

Fig.6 Comparison results between the ANNC method and the proposed method

Fig.7 Comparison results between the CMPC methods with different parameters and the proposed method

5 Conclusion

In this paper,a sliding mode-based adaptive tube MPC strategy was proposed to solve the tracking control problem of robotic manipulators with state constraints and model uncertainty.The objective function and feedback correction design of MPC were studied,and the presented control framework consisted of three parts: nominal model, nominal MPC by introducing sliding mode,and the auxiliary controller based on node-adaptive NNs.First, the linear nominal model of the robotic manipulator was constructed according to the HOFA system approach, which was used as the predictive model.Then,the nominal state constraints was transformed into input constraints by solving the dynamic differential equations, and the objective function of nominal MPC was designed by introducing the sliding mode.Based on the proposed nominal MPC strategy,the accurate and stable tracking of the desired trajectory by the nominal system was realized.After that,the auxiliary controller was developed based on node-adaptive NNs.The adaptive adjustment method for neural nodes of NNs and the adaptive updating laws of NNs’weights were constructed.Therefore, the nonlinear uncertainty of the robotic manipulator was compensated in the feedback correction section,rather than was estimated by the learning predictive model.The estimated deviation between the nominal and actual states was also limited to the tube invariant set.It was proved that all variables of the closedloop system were UUB according to Lyapunov theorem,and the effectiveness of the proposed control method was illustrated by contrastive experimental results.

Fig.9 Results under the proposed method in the presence of observation errors

Funding This work was supported in part by the National Natural Science Foundation of China under Grant 91948303 and 6210020614,in part by the Strategic Priority Research Program of Chinese Academy of Science under Grant XDB32050100.

Data availability The datasets generated during the current study are available from the corresponding author on reasonable request.

Its solution is expressed as

Appendix A

The nominal system of the robotic manipulator in this paper is defined as

Substituting(A3)intoe¯At,one has

where