Contracted product of hypermatrices via STP of matrices
Daizhan Cheng·Min Meng·Xiao Zhang,3·Zhengping Ji,4
Abstract An equivalent definition of hypermatrices is introduced.The matrix expression of hypermatrices is proposed.Using permutation matrices,the conversion between different matrix expressions is revealed.The various kinds of contracted products of hypermatrices are realized by semi-tensor products(STP)of matrices via matrix expressions of hypermatrices.
Keywords d-hypermatrix·Matrix expression·Permutation matrices·Contracted product·Semi-tensor product(STP)
1 Introduction
The hypermatrix is an extension of the matrix to the higher order case (orderd≥3).It has found wide application in many fields,including computer science[1],signal processing [2], statistics [3], etc.We refer to [4] for a systematic introduction to the hypermatrices,and to[5,6]for some later developments.
A generalized matrix product,called the semi-tensor product(STP),was proposed two decades ago[7].Since then it has been rapidly developed both in theoretical aspects and in various applications[8,9].For example,it has been applied to the study of Boolean and finite-valued networks(see survey papers [10–13]); finite games (see survey paper [14]);finite automata (see survey paper [15]); dimension-varying systems[16,17],etc.
Later, in addition to the original matrix-matrix STP,the matrix–vector STP was proposed [18] and applied to dimension-varying dynamic (control) systems [17, 19].Recently,the STP of hypermatrices has also been introduced[20].It seems possible that some new unknown STPs will appear in the future.In the early days, the (matrix-matrix)STP is said to be a generalization of the conventional matrix product.With the appearance of new STPs,this explanation does not seem to be sufficient.
The purpose of this article is to show that in essence,STPs are representations of multilinear mappings over hypermatrices.More precisely,the hypermatrices are first expressed in their matrix forms,then the multilinear mappings over them can be executed by STP over their matrix expressions.For this purpose,the conversion of different matrix expressions of hypermatrices plays an important role.
The rest of this paper is organized as follows: Section 2 considers how to transform a hypermatrix into its distinct matrix expressions.The permutation matrix is also introduced for transforming among different matrix expressions.Section 3 shows how to realize the contracted product of hypermatrices over their matrix expressions.In Section 4,the STP is used to perform the contracted product of hypermatrices,which shows that STPs are essentially multilinear operators over hypermatrices.
Before ending this section,we give a list of the notations used in this paper:
2 Matrix expression of hypermatrices
2.1 Set-based hypermatrix
Definition 1 [4] Forn1,...,nd∈N, a functionf: Fn1×···×Fnd→F is called ad-th order hypermatrix of dimensionsn1,n2,...,nd(over F), or an orderdhypermatrix or ad-hypernatrix.Ad-hypermatrix is also denoted byA=[ai1,...,id].
From a set point of view, a hypermatrix consists of two ingredients:
(i) a set of data
(ii) an order overDA,which makesDAa totally ordered set.In other words,each element inDAhas a fixed position,just as in the case of a matrix.
To make the order ofDAprecise, we introduce a set of ordered indices,ID,as follows:
which stands for a set of data as in(1),where(α1,...,αd)is a permutation of〈d〉.The order of ID is determined as follows:ap1,...,pd≺aq1,...,qdif and only if there is ans∈〈d〉,such thatpi=qi,i If(α1,...,αd)=(1,2,...,d),thecorrespondingordered set of indices is called a natural order,denoted byi〈d〉. Based on the above argument, a hypermatrix can be defined alternatively as follows. Definition 2 Forn1,...,nd∈N,a hypermatrix(over F),is a set of orderddata as in(1)with a set of ordered indices as ID(i〈d〉;n1,...,nd). To apply classical matrix analysis to hypermatrices, the matrix expression of hypermatrices is a key issue. Letr=(r1,r2,...,rd)be a set of indices,and be a partition,wherer1∩r2=∅,andp+q=d.For ease of notation,we will assume that the elements in two subsets inherit the element order of the original set,unless otherwise stated. Definition 3 Given a hypermatrixA=[ar1,r2,...,rd].For each partition there is a matrix expression ofA,denoted by where Moreover, the elements inare {ar1,r2,...,rd}, which are arranged by ID(r1;nri1,nri2,...,nri p)for rows,and by ID(r2;nr j1,nr j2,...,nr jq)for columns. Remark 1(i)pis called the contra-variant order ofandqis called the co-variant order of (ii) Ifp= 0,then we sets= 1,and ifq= 0,then we sett=1. (iii) Particularly,in(3)we require a natural order unless it is otherwise stated.That is,ri1 Example 1GivenA=[ai1i2i3]∈F2×3×2.Then Definition 4 (i)VA:=is called the(row)vector expression of hypermatrixA. (ii)MA:=is called the contra-variant 1 matrix expression(briefly,matrix-1 expression)of hypermatrixA. Definition 5 Letxi∈Fni,i∈〈d〉. (i)x:=is called a hypervector of orderd. (ii) The set of orderdhypervectors with corresponding dimensions is denoted by Fn1■···■nd. Note that the components ofxcan be expressed as whereis their-th component ofxr.Hence it is clear that com(x)(or briefly hypervectorx)is a hypermatrix of orderd.Moreover,it is obvious that Proposition 1 Fn1■···■nd⊂Fn1×···×nd is a subset of hypermatrices. Definition 6 [4] (i) Givenad-hypermatrixassumeσ∈Sd.Theσ-transpose ofAis It is obvious that a matrix is a 2-hypermatrix,so the above general definitions coincide with the corresponding definitions for matrices. Proposition 2A2-hypercubic A∈Fn×n is(skew-)symmetric,if and only if,MA is(skew-)symmetric. Proposition 3Let A∈Fn1×···×nd and r⊂d=〈d〉.Then Remark 2The above arguments stand true even when F is a set of perfect hypercomplex numbers (PHNs) [21].In fact,most of arguments throughout this paper also hold for PHNs. Next, we recall the permutation matrix [22], which is a generalization of swap matrix. • Step 1:Define • Step 2: Arrange {σ(i)|i∈ [1,d]} into an increasing sequence as That is, Set an index order as • Step 3: Example 2Letd= 3,n1= 2,n2= 3, andn3= 5.We constructWσ:=Wσ[2,3,5]. (1)σ1= identity (i.e., [1,2,3] → [1,2,3]): We haveWσ1 =I30. (2)σ2=(2,3)(i.e.,[1,2,3]→[1,3,2]):Then (3)σ3=(1,2)(i.e.,[1,2,3]→[2,1,3]): Similarly,we have (4)σ4=(1,2,3)(i.e.,[1,2,3]→[2,3,1]): We have (5)σ5=(1,3,2)(i.e.,[1,2,3]→[3,1,2]): Then (6)σ6=(1,3)(i.e.,[1,2,3]→[3,2,1]): Then Whenn1=n2= ··· =nd:=nthe corresponding permutation is briefly denoted by Since this kind of permutation matrices are of particular importance, we write some of them explicitly in the“Appendix”. Some basic properties of permutation matrices are presented in the following proposition,which follows from the definition immediately. Proposition 4 (i) (ii)Let σ,μ∈Sd.Then The following proposition shows the basic function of permutation matrices. Proposition 5 [22]Assume xi∈Fni,i∈〈d〉,σ∈Sd.Then As an immediate consequence, we have the following result,which shows how to calculateAσ. Proposition 6Let A∈Fn1×···×nd be a hypermatrix of order d.Then ProofProposition 5 implies that Taking transpose on both sides yields(10). Definition 8 (i) LetA=[ai,j]∈Fm×nbe a matrix.Then is called the column stacking form ofA. (ii) Letx∈Fnands|n.Say,n=st.Then (iii) LetA∈Fm×nands|(mn).Then is called thes-row stacking form ofA. is called thes-column stacking form ofA. Proposition 7 [23]Let A∈Fm×n,X∈Fn×q,and Y∈Fp×m.Then Denote by Proposition 8Let A∈Fm×n.Then Conversely, Proof(19) and (20) come from Proposition 7 immediately.(21)follows from the definition.■ By definition and(21),we have Setir=(i1,...,ir)⊂d=〈d〉,and denote The following proposition shows how to convert the matrix expression of a hypermatrix to its vector form and vise versa. Proposition 9Given A= [ai1,...,id] ∈ Fn1×···×nd,ir=(i1,...,ir)⊂d=〈d〉,and σir is as in(23), Then (i)(Vector form to matrix form) (ii)(Matrix form to vector form) ProofFor(i),we have As for(ii),using(10)and(19),we have Using(24)and(25),we obtain the formula transforming one matrix form to another. Corollary 10Let ir,σir be as in Proposition9,and js=(j1,...,js)and σ js:d→(js,djs).Then where the×between MA and MB is the conventional matrix product. Definition 9 can be extended to the case of multiple common indices. Definition 10 LetA= [ai1,...,id] ∈ Fn1×···×nd,B=[b j1,...,jr]∈Fm1×···×mrwith wheres≤ min(d,r) is the number of equal dimension indices.Define where where a caret over any entry means that the respective entry is omitted. Proposition 12 where the×between MA and MB is the conventional matrix product. Example 3AssumeA= [ai1,i2,i3] ∈ F2×3×4,B=[b j1,j2,j3]∈F4×5×3with natural ID,calculate We have ThenC∈F2×5with A particular case isA= [ai1,...,id] ∈Fn1×···×nd,B=[bir1,...,irs] ∈Fnr1×···×nrs, andrs:= {r1,...,rs} ⊂d:=〈d〉.Then we briefly denote We call this kind of product the onto contracted product.They are of particular importance. In the onto contracted product,Acan be considered as a multilinearmappingfromFnr1×···×nrstoFn1×···×ˆnr1×···×ˆnrs×···×nd. Proposition 13Assume A∈Fn1×···×nd and B∈Fnr1×···×nrs,where rs:= {r1,...,rs} ⊂d.The contracted product of A and B,denoted by can be obtained by one of the following two equivalent formulae: (i)LetThen (ii)Let σ∈Sd be the permutation Then Definition 11 (i) LetA∈ Fn1×···×nd×nd+1×···×n2d,B∈Fn1×···×nd, wherend+i=ni,i∈ 〈d〉.ThenA:Fn1×···×nd→Fn1×···×ndis defined by This contracted product is called a unary operator on Fn1×···×nd. (ii) LetA∈Fn1×···×n3d,B,C∈Fn1×···×nd,wheren2d+i=nd+i=ni,i∈〈d〉.ThenA:Fn1×···×nd×Fn1×···×nd→Fn1×···×ndis defined by This contracted product is called a binary operator on Fn1×···×nd. (iii) Similarly,we can definekargument(i.e.,khypermatrix)operators fork≥3. This section shows that a fundamental faculty of STP is to realize the contracted product of hypermatrices.This may help us to understand what is the essential meaning of STP.For this purpose, the hypermatrices are first expressed in their matrix expressions.The STPs are operators on matrices.When the hypermatrices are transformed into their matrix forms, the action of operators (especially of certain contracted products) on their objective hypermatrices can be realized by the action of STPs on the matrix expressions of the corresponding hypermatrices.Figure1 shows this process. Since there are many possible multilinear operators,including contracted products,over different hypermatrices,the corresponding operators over their matrix expressions are diverse.To express these operators,the STPs are also diverse. From linear algebra one sees that the matrix product has two fundamental types: (1) Matrix-matrix (M-M) product:it represents the composition of two linear mappings.(2)Matrix–vector (M-V) product: it realizes a linear mapping over a vector space (or between two vector spaces).Fortunately, when the dimensions are compatible, the classical matrix product can realize these two functions simultaneously. When the conventional matrix product is extended to STP,where the dimensions are not compatible, an STP cannot realize these two functions simultaneously.Therefore, we need to distinguish between M-M STP and M-V products.First,we review the classical STPs[17]: Definition 12 (i) LetA∈Fm×n,B∈Fp×qandt=lcm(n,p).The M-M STP ofAandBis defined as (ii) LetA∈Fm×n,x∈Fpandt= lcm(n,p).The M-V STP ofAandxis defined as (iii) Letx∈Fm,y∈Fnandt= lcm(m,n).The vectorvector(V-V)STP ofxandyis defined as Define Then the M-M STP can be considered as the product overM;the M-V STP can be considered as the action ofMon R∞;and the V-V STP can be considered as an inner product over R∞.It is obvious that they are the generalizations of the corresponding matrices with matrix-matrix or matrix–vector product, or vectors with vector product.Furthermore, they satisfy the following general properties. Proposition 14 (i)(Associativity) (ii)(Distributivity)For A,B,C∈M,x,y,z∈R∞, Remark 3M-V and V-V STPs are not so commonly used as M-M STP.We elaborate on this a little bit more. • Topology on R∞: Considerx∈Rp,y∈Rq,(x,y∈R∞),t= lcm(p,q).Define then R∞becomes a(pseudo-)vector space. Furthermore,we define (i) (Inner product): (ii) (Norm): (iii) (Distance): With this distance R∞becomes a topological space[17]. • Linear dynamic systems over R∞: A linear dynamic system over R∞is defined by It is a cross-dimensional system[24]. LetΠ:= [ci1,...,id]where ID = ID(i1,...,id;n1,...,nd)is a hypermatrix of orderd.Then the following result is well known. Proposition 15Themultilinearmappingπ canbecalculated by Proposition 16Themultilinearmappingπ canbecalculated by Example 5(i) Cross product on R3: Consider the cross product onR3,denoted by →×.Denote by It follows that (ii) General linear algebra gl(2,R).Denote by Remark 4(i) Roughly speaking,in classical sense,an STP of matrices is a multilinear operator over hypermatrices.To be precise,when the hypermatrices are expressed into their matrix forms,the STP works as a matrix product. (ii) Since multilinear mappings over hypermatrices can be various,there can also be various STPs. (iii) When partial arguments are known,an operator becomes a restricted operator over the remaining arguments.In this case, STP combined with swap matrices becomes more powerful. We give two examples for this. Example 6AssumeVis ann-dimensional vector space over F.T:Vr×(V∗)s→F is a tensor of covariant orderrand contra-variant orders.Let,i∈〈n〉 be a basis ofVandωi=()T,i∈〈n〉be the dual basis of the dual spaceV∗,and set Then is a hypermatrix of orderr+s. Construct, wherejs:=(j1,...,js),ir:=(i1,...,ir). Forω1,...,ωs∈V∗,x1,...,xr∈V,we have Example 7[4] In statistical mechanics, the Yang–Baxter equation is given as follows: LetR= [ri1,i2,i3,i4] ∈FN×N×N×N.Then we have(in our notation): We express(40)into matrix form as follows: ExpressingRinto matrix form,we have Fig.2 ×versus Hence,the RHS of(40)becomes Hence,(40)implies that In this paper, the matrix expression of hypermatrices was first proposed.As an auxiliary tool, the permutation matrices have also been discussed in detail.It is utilised to reveal certain properties of the matrix expression of hypermatrices.Then we showed that the STPs of matrices are essentially the multilinear operators of hypermatrices(including hypervectors).The operators over hypermatrices including contracted products,are realized by STPs through the matrix expression of hypermatrices.In fact,the actions of STP over hypermatrices can be considered as a generalization of the actions of the conventional matrix product over matrices.This fact can be demonstrated by Fig.2. The aforementioned hypermatrix product are called“contracted type", since it contracts an index of both hypermatrices and concatenate them together; there is another type of hypermatrix product of “compound type", which can be viewed as a natural generalization of the STP to hypermatrices;we will discuss them as well as give applications in our future work. Appendix In the following,some permutation matrices are listed. 1.d=3,n=2:2.2 σ-transpose of hypermatrices

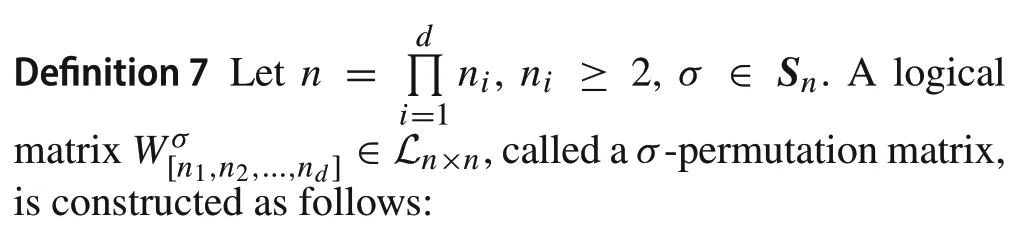
2.3 Conversion of matrix expressions
3 Contracted product of hypermatrices

4 STP realization of contracted product of hypermatrices
4.1 Classical STPs
4.2 STP for vector expression of hypermatrices


4.3 STP for matrix-1 expression of hypermatrices


4.4 STP for general matrix expression of hypermatrices


5 Conclusion




 Control Theory and Technology2023年3期
Control Theory and Technology2023年3期
