Heterogeneous multi-player imitation learning
Bosen Lian·Wenqian Xue·Frank L.Lewis
Abstract This paper studies imitation learning in nonlinear multi-player game systems with heterogeneous control input dynamics.We propose a model-free data-driven inverse reinforcement learning(RL)algorithm for a leaner to find the cost functions of a N-player Nash expert system given the expert’s states and control inputs.This allows us to address the imitation learning problem without prior knowledge of the expert’s system dynamics.To achieve this,we provide a basic model-based algorithm that is built upon RL and inverse optimal control.This serves as the foundation for our final model-free inverse RL algorithm which is implemented via neural network-based value function approximators.Theoretical analysis and simulation examples verify the methods.
Keywords Imitation learning·Inverse reinforcement learning·Heterogeneous multi-player games·Data-driven model-free control
1 Introduction
Imitation learning is a popular approach where a learner mimics the demonstrated behaviors of an expert, based on limited samples of the expert’s demonstrations.It is commonly addressed through two main approaches: behavioral cloning[1,2]and inverse reinforcement learning(RL)[3,4].The former tackles the problem by learning a policy directly from expert demonstrations,treating it as a supervised learning task.In contrast, inverse RL focuses on reconstructing the underlying objective function, such as cost or reward functions,that best explain the expert’s demonstrations.The objective function serves as a higher-level index,providing transferability and robustness in control problems.Notably,inverse RL requires significantly fewer data[5]compared to behavioral cloning[6],making it more efficient in terms of sample utilization.The success of inverse RL is shown in a wide range of applications such as autonomous driving [7,8],anomaly detection[9,10],and energy management[11].
Inverse RL and inverse optimal control(IOC)share fundamental principles and are often considered as closely related concepts.The conventional IOC methods in control systems [12] typically rely on system dynamics to solve the objective function.In contrast, inverse RL techniques in the machine learning field can construct objective functions using only demonstrated expert trajectories,without explicitly requiring system dynamics.Notably,model-free inverse RL algorithms have been developed for single-player and multi-player Markov decision processes[13–16].Inspired by the success of inverse RL and IOC, researchers have combined these approaches to develop model-free data-driven inverse RL methods for control systems with single-player input[17,18]and two-player games[19–22].
Control problems involving multiple inputs and players are prevalent in practical applications.Multi-player games[23]provide a framework for modeling the decision-making process of multiple players who interact with each other.In these games, each player, corresponding to the control input, seeks to find a Nash equilibrium solution in non-zero-sum games.To compute such a solution for each player, two primary online computational approaches have emerged:model-free off-policy RL[24–27]and online datadriven actor-critic methods [28–30].Building upon these developments, data-driven inverse RL has been studied for multi-player games[31,32].
This paper studies the learner-expert imitation learning problem in the context of nonlinear heterogeneous multiplayer game systems.Specifically,we consider the scenario of non-zero-sum games and propose a data-driven inverse RL approach for the learner to find the cost functions of all players given expert demonstrations without knowing system dynamics.The contributions of this paper are twofold.First,we propose a data-driven model-free inverse RL algorithm without knowing any system dynamics.This is in contrast to previous work [31] that requires knowledge of the input dynamics of all heterogeneous players.Second,we address a practical limitation present in previous approaches[31,32],which required the learner and expert to have the same initial states in the learning process.Whereas,this paper removes this requirement.
2 Notations and preliminaries
2.1 Notations
R, Rn, and Rn×mdenote the set of all real numbers,n-column vectors, andn×mmatrices, respectively.‖·‖defines the 2-norm.Forx∈ Rnandy∈ Rm,x⊗y≜ [x1y1,...,x1ym,x2y1,...,x2ym,...,xn ym]T.ForA=(ai j) ∈Rn×m, vec(A) ≜[a11,...,a1m,a21,...,a2m,...,anm]T.For a symmetric matrixA=(ai j)∈Rn×n,vem(A)≜[a11,a12,...,a1n,a22,...,an-1,n,ann]T.λmindenotes the minimum eigenvalue.Indenotes the identity matrix of sizen.
2.2 Expert system
Consider theN-player expert system as
wherexe(t)∈Rnis the expert state,u je(t)∈Rm jis the optimal control input of expert playerj,j∈N≜{1,2,...,N}associated with some underlying cost function.f(xe) andg j(xe)denote expert’s system dynamics.
Assumption 2 Assumegi/=g jfori/=jin (1), wherei,j∈N.
Assumption 2 defines the multi-player game systems with heterogeneous control inputs.
Assume the underlying cost function that each expert playerjminimizes is

According to optimal control theory[33],the optimal control inputsu jeof the expert system(1)that minimize the cost functions(2)are
where ∇Vje(xe(t)) satisfy the coupled Hamilton–Jacobi equations
2.3 Learner system and imitation learning problem
Consider aN-player learner system
wherex∈Rnandu j∈Rm jare the learner state and control input of playerj∈N, respectively.The dynamics of the learner are the same as the expert’s.Let us set the cost function for playerjas
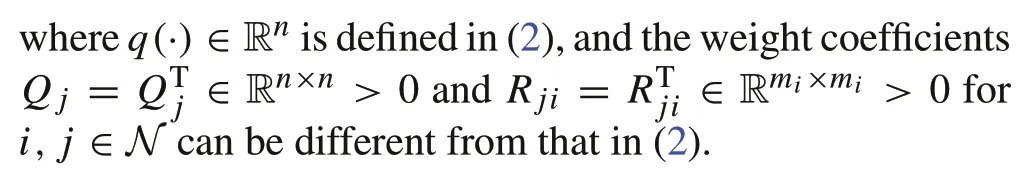
Similar to the optimal control process in (1)–(4), the learner’s optimal control inputs that minimize(6)are
where ∇Vj(x) satisfy the coupled Hamilton-Jacobi equations
If each learner player imitates each learner player’s behavior, then both systems will have the same trajectories.To achieve this goal,we propose the following assumptions and the imitation learning problem.
Assumption 3 The learner knowsq(·) and its own weight coefficientsQ jandR ji,i,j∈Nin(6),but does not know the expert’s weight coefficientsQ jeandR(ji)e,i,j∈Nin(2).
Assumption 4 The learner has access to the measurement data of the expert’s state and inputs,i.e.,(xe,u je),j∈N.
It is known that different weight coefficient pairs can yield thesameoptimalcontrolsinIOCproblems[34,35].We,thus,give the following equivalent weight definition from[31].
Definition 2 AnyQ j> 0 ∈Rn×nandR ji> 0 ∈Rmi×mi,i,j∈Nin (8) that make (7) yieldu∗j=u jeandx=xewhereu jeis defined in(3)are called equivalent weights toR(i j)eandQ je.
To guarantee the existence of the above equivalent weight givenf, heterogeneousg j,j∈N, andq, we make the following assumption.
Assumption 5 For the system with dynamicsq(·),f(·)andg j(·),there exists at least one equivalent weight toQ je≥0 with the selectedR ji>0,i,j∈N.
Heterogeneous multi-player imitation learning problem Under Assumptions 1–5,given anyR ji>0,the learner aims to infer an equivalent weight toQ jefor (6) for each playerj∈Nwithout knowing system dynamics,such that it mimics the expert’s demonstrations,i.e.,
3Model-based inverse RL for heterogeneous multi-player games
To solve the imitation learning problem of heterogeneous multi-player game systems, this section presents a modelbased inverse RL algorithm to find an equivalent weight ¯Q jgivenR ji>0usingexpertdemonstrations(xe,u1e,...,uNe).The algorithm has a two-loop iteration structure,where the inner loop is the RL process to learn optimal control and the outer loop is the IOC process to update weight coefficients.
3.1 Algorithm design
We first design a model-based inverse RL Algorithm 1 presented as follows.It has two iteration loops.We selectR ji> 0 and keep them fixed.The inner iteration loop, (9)and(10),is RL process to update the value function and control input for each playerjthat are optimally associated with the current weight coefficientsQsjandR ji> 0.The converged solutionsusjare the optimal solutions to (7)–(8) for each outer-loop iterations.Then, the outer loop iteration,i.e., (11) based on IOC, is to updateQsjtoward the equivalent weight ¯Q jusing the demonstrated expert trajectories data(xe,u je).Note thatρ j∈(0,1]is the tuning parameter that can adjust the update speed.
3.2 Convergence and stability
Theorem 1Algorithm1solves the imitation learning problem of heterogeneous multi-player systems by learning uniformly approximate solutions of the equivalent weight¯Q j,j∈N at limited iteration steps.
ProofThe inner loops are the standard RL policy iterations.The convergence of it at any inner iteration loops can be referred to [36].The policy iteration is proved to be quasi-Newton’s method in a Banach space[37–39]that yields the converged(usj,Vsj),whereVsjis the optimal value andusjis the optimal control input at outersloop.
We now prove the convergence of outer loops.(11)implies that

Algorithm 1 Model-based inverse RL for heterogeneous multi-player games 1: Initialization:Select R ji >0,initial Q0j >0,stabilizing u00j ,small thresholds e j and ε j for all j ∈N,and ρ j ∈(0,1].Set s =0.2: Outer s-th iteration 3: Inner k-th iteration:Set k =0.4: Solve value functions by 0=qT(x)Qsjq(x)+Nimages/BZ_23_579_506_616_541.png(usk images/BZ_23_853_493_873_529.pngimages/BZ_23_1001_493_1021_529.pngTimages/BZ_23_1037_502_1045_537.pngimages/BZ_23_1045_493_1065_529.pngimages/BZ_23_1352_493_1372_529.pngi )TR jiuski +∇Vsk j (x)f(x)+Nimages/BZ_23_1183_506_1219_541.pnggi(x)usk.i=1 i=1 i (9)5: Update control inputs by us(k+1)j (x)=-1 2 R-1 j j gTj(x)∇Vskj (x).(10)6: Stop if‖Vsk j -Vs(k-1)j ‖≤ei,then set usj =uskj ,otherwise set k ←k+1 and go to step 4.7: Outer s-th iteration:Update Qs+1 j using(xe,u1e,...,uNe)by qT(xe)Qs+1 j q(xe)=ρ jimages/BZ_23_613_948_632_984.pngu je(xe)-usj(xe)images/BZ_23_877_948_896_984.pngTR j jimages/BZ_23_980_948_999_984.pngu je(xe)-usj(xe)images/BZ_23_1244_948_1263_984.png+qT(xe)Qsjq(xe).(11)8: Stop if‖usj -u je‖≤ε j,otherwise set u(s+1)0 j =usj,s ←s+1,and go to step 3.
It shares similar principles of sequential iteration in, for example,numerical algorithms[40].Given initial> 0,(12)implies
and

which implies

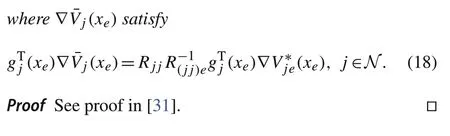
4 Model-free inverse RL for heterogeneous multi-player games
The inverse RL Algorithm 1 needs to know heterogeneous multi-player system dynamicsf,g1,...,gN, which may not be fully known in reality.To address this, we develop a completely model-free data-driven inverse RL algorithm in this section.The algorithm leverages the off-policy RL technique and neural networks.It uses only measurement data of(xe,u1e,...,uNe)to find a ¯Q jthat optimally yieldsuje(3)for the imitation learning problem.
4.1 Off-policy inverse RL design
Based on Algorithm 1, we present two steps to design the model-free data-driven inverse RL algorithm.
Step 1:Find a model-free equation that replaces(9)and(10).Off-policy integral RL[41,42]is used in Algorithm 1’s inner loops.Towards this end,we rewrite(8)as
whereare the updating control inputs.
In addition,we have
Putting(19)into(20)and then considering(9),we have
Based on[25],we define the following control inputs for the purpose of model-free off-policy heterogeneous multiplayer RL

Remark 1A simple understanding of theu jiin (22) withj/=iis that they are auxiliary variables to solveu jiin(22)withj=i.Note thatR ji∈Rmi×mi.
The model-free inverse RL algorithm for imitation learning in heterogeneous multi-player games is shown below.
Theorem 2Algorithm2has the same solutions as Algorithm1.
ProofTaking the limit to(24)of the time intervalδtyields
One has

Algorithm 2 Model-free inverse RL for imitation learning in heterogeneous multi-player games 1: Initialization:Select R ji >0,initial Q0j >0,stabilizing u00j ,small thresholds e j and ε j,and ρ j ∈(0,1]for all j ∈N.Set s =0.2: Outer s-th iteration 3: Inner k-th iteration:Set k =0.4: Solve value functions and control inputs for each player j by Vsk j (x(t +δt))-Vskj (x(t))-images/BZ_25_711_484_729_520.png t+δt Nimages/BZ_25_810_506_847_541.png(us(k+1)ji )TR ji(ui -uski )dτ (24)images/BZ_25_378_594_396_629.png t+δt t i=1images/BZ_25_474_603_493_639.pngimages/BZ_25_969_603_988_639.png=-Nimages/BZ_25_737_616_774_651.png(usk dτ.t qT(x)Qsjq(x)+i=1 i )TR jiuski j -Vs(k-1)j ‖≤e j,then set usj =us(k+1)j ,otherwise set k ←k+1 and go to step 4.6: Outer s-th iteration:Update Qs+1 j using measurement data of(xe,u je)by(11).7: Stop if‖usj -u je‖≤ε j,otherwise set u(s+1)0 j =usj,s ←s+1,and go to step 3.5: Stop if‖Vsk
which implies that(24)is equivalent to(9).In addition,the outer loop formulation is the same.This shows that Algorithms 2 and 1 have the same solutions.■
4.2 Neural network-based implementations
Solving directly Algorithm 2 is difficult.Therefore, we implement it via neural networks(NNs).We design two NNbased approximators forin (24) andin (22).According to[43,44],the two approximators are defined as
With approximators (27) and (28), we rewrite (24) with residual errorsas
With Kronecker product,(29)is rewritten as

where
Based on(30),(31),(29)can be solved using batch least squares as

which can be rewritten as
where
To use batch least squares method to solve, we define
Similarly,we sampleω≥n(n+1)/2 data tuples in(35),such that rank(XTe Xe) =n(n+ 1)/2.We, thus, uniquely solve forby
5 Simulations
This section verifies the model-free inverse RL Algorithm 2 with both linear and nonlinear multi-player Nash game systems.
5.1 Linear systems
Consider the expert as a 3-player Nash game system with dynamics matrices
The learner has identical dynamics.
We assume the cost function weights of the expert are
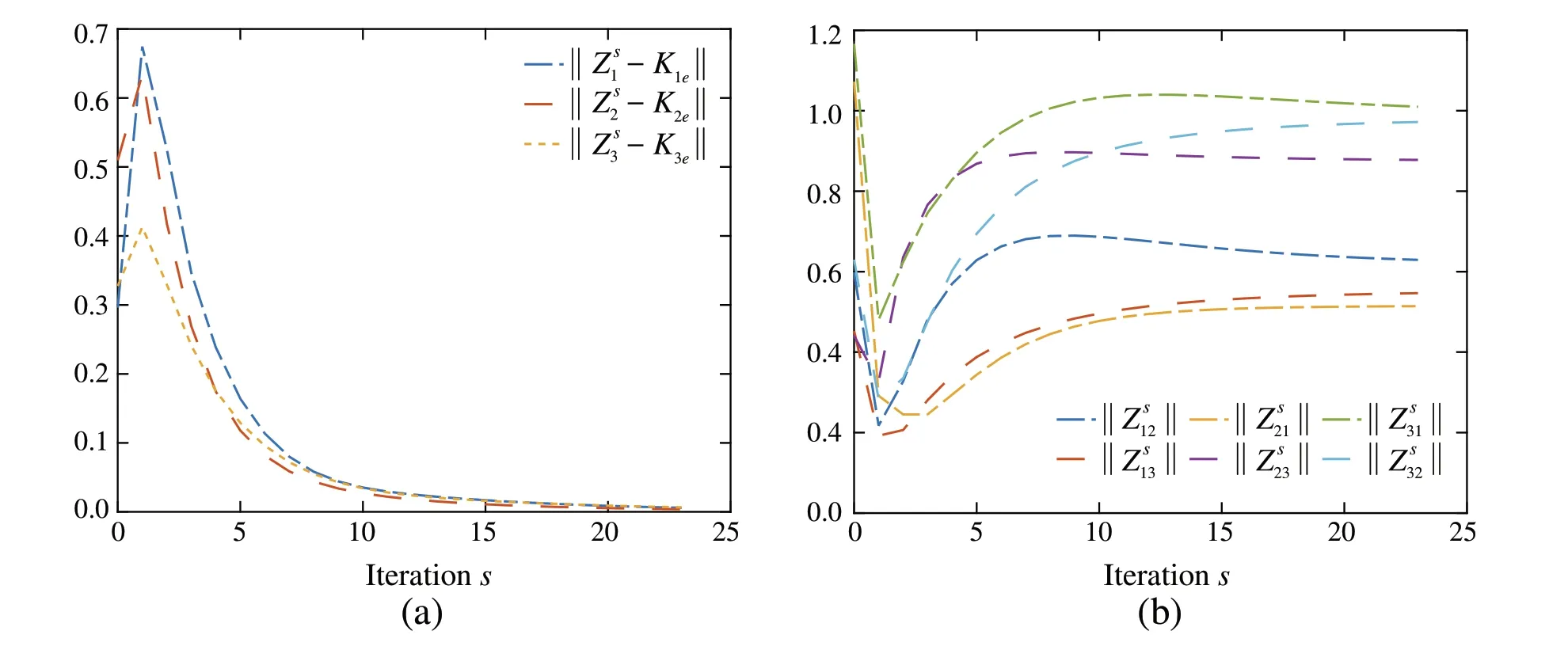
Fig.1 a Convergence of control input NN weights to K je.b Convergence of control input NN weights,where i /= j and i, j ∈{1,2,3}
which yield the optimal control feedback gains(in terms ofu je=-K jexe)

5.2 Nonlinear systems
Consider the expert as a 3-player Nash game system with dynamics matrices

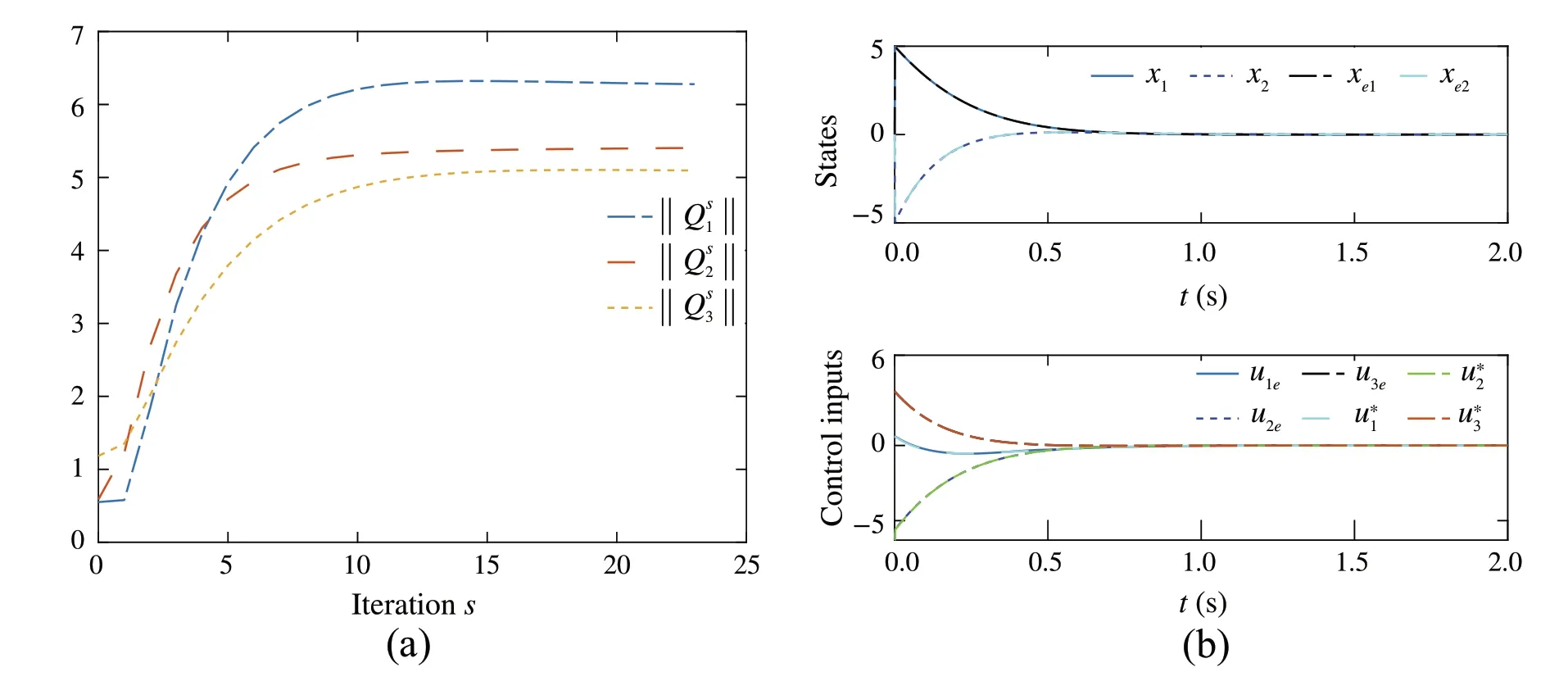
Fig.2 a Convergence of cont function weight .b Trajectories of the expert and the learner using the converged control policies
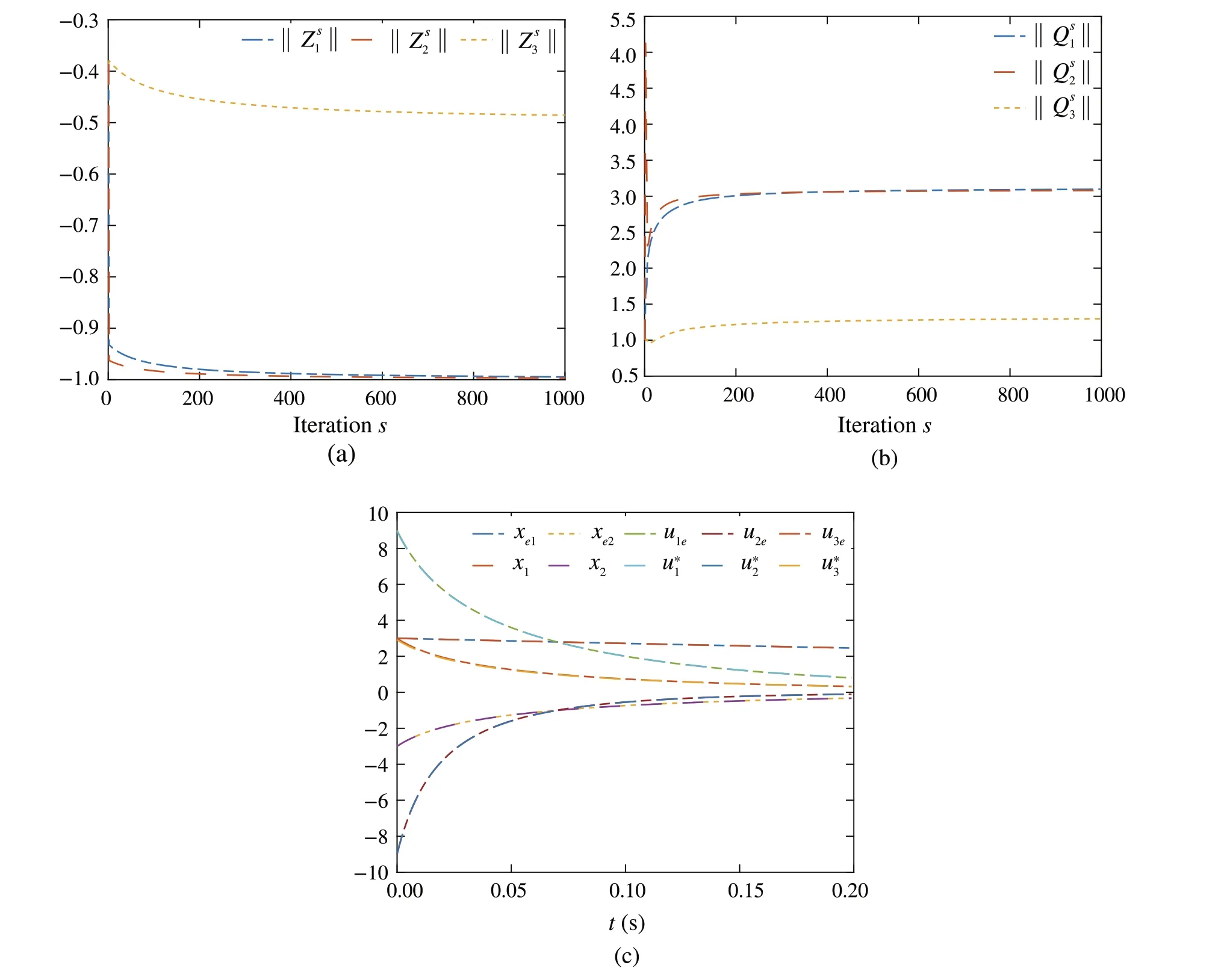
Fig.3 a Convergence of control input NN weights .b Convergence of cost function weights ,where j ∈{1,2,3}.c Trajectories of the expert and the learner using the converged control policies
6 Conclusions
This paper studies inverse RL algorithms for imitation learning of multi-player game systems where different control input dynamics are different.We propose a model-free data-driven algorithm to reconstruct the cost functions of a demonstrated multi-player system and yield the same expert’s trajectories.The algorithm is implemented via value function approximators.Simulation examples verify the effectiveness of the proposed methods.In the future,we consider to extend the work to inverse RL for multiagent systems with multiple control players.
 Control Theory and Technology2023年3期
Control Theory and Technology2023年3期
- Control Theory and Technology的其它文章
- Distributed Nash equilibrium seeking with order-reduced dynamics based on consensus exact penalty
- A Lyapunov characterization of robust policy optimization
- State observers of quasi-reversible discrete-time switched linear systems
- Input-to-state stability and gain computation for networked control systems
- Semi-global weighted output average tracking of discrete-time heterogeneous multi-agent systems subject to input saturation and external disturbances
- A hybrid data-driven and mechanism-based method for vehicle trajectory prediction
