基于几何相位的线偏振聚焦全介质超透镜的设计
王玲玉 宋秋阳 苗玉 高秀敏


摘要:超透镜凭借其独特的优势逐渐取代或补充了传统的折光和衍射透镜,从而领先小型化高性能光学设备和系统。这种小型化有望带来紧凑的纳米级光学设备,应用于相机、照明、显示器和可穿戴光学。但在传统的超透镜设计中,几何相位通常需要左右旋圆偏振光的手性限制。为了使其不再局限于左旋圆偏振光(LCP)和右旋圆偏振光(RCP)入射,设计了基于几何相位的全介质超透镜,实现了线偏振光的近场聚焦,其与超表面滤光片主要输出波长(可见光波段)一致。采用有效时域差分法研究并验证了超透镜各变量对光场聚焦特性的影响,超透镜等其他超表面光学元器件前所未有的设计自由度将极大地扩大微光学和集成光学的应用领域。
关键词:几何相位;全介质超透镜;线偏振光聚焦
中图分类号: O 436.3 文献标志码: A
Design of all-dielectric metalens with linearly polarized focusing based on Pancharatnam-Berry phase
WANG Lingyu ,SONG Qiuyang,MIAO Yu ,GAO Xiumin
(School of Optical-Electrical and Computer Engineering, University of Shanghai for Science and Technology, Shanghai 200093)
Abstract: Metalens have gradually replaced or supplemented traditional refractive and diffraction lenses with their unique advantages, leading to further miniaturization of high-performance optical devices and systems. This miniaturization is expected to lead to compact nanoscale optical devices for applications in cameras, lighting, displays, and wearable optics. However, in conventional metalens designs, the Pancharatnam-Berry (PB) phase usually requires the chirality limitation of left and right circularly polarized light. In order to avoid the incident limitation of the linearly polarized light by the left-handed circular polarization (LCP) and right-handed circular polarization (RCP), an all-dielectric metalens based on PB phase was designed to achieve near-field focusing of linearly polarized light. It coincides with the main output wavelength (visible band) of the metasurface filter. The effects of various variables on the focusing properties of the light field were studied and verified by effective time-domain difference simulation in this paper. The unprecedented design freedom of metalens and other metasurface optical components will greatly expand the application fields of micro-optics and integrated optics.
Keywords: Pancharatnam-Berry phase ;all-dielectric metalens ;linearly polarized light focusing
引 言
傳统的聚焦透镜体积大,制造精度高,成本高,耗时长,且受天然材料折射率的限制[1]。这些都是极大的限制,特别是对便携式和可穿戴设备等应用而言。近年来,超透镜作为一种具有平面构型透镜功能的超表面器件,进一步开发了超表面技术的潜力,为小型化、便携式成像镜头和可穿戴设备开辟了全新的发展方向[2]。同时,它将革新现有传统光学器件及光学系统。超表面聚焦透镜作为成像和传感等相关应用的重要器件,一直是学者们关注的焦点,在物理、生物、医学等科学领域有着重要的应用[3-7]。
超表面原理一般分为两类:一类是基于天线共振调制,另一类是基于几何相位调制[8-9]。由于几何相位调制具有灵活性和简单性,利用几何相位调制设计超透镜成为近年来的研究热点。 Chen 等[10]提出了利用金属薄膜上的方孔调制光相位的方法,设计了数值孔径为0.583、焦距为240?m的结构透镜,得到的焦斑大小达到衍射极限的结果。Kang 等[11]提出了一种由相位不连续的各向异性孔径天线组成的超薄超材料,将圆偏振光完全转换为交叉偏振光,在衍射极限附近可以弯曲或紧密聚焦。Aieta 等[12]设计的无像差平面透镜和轴锥透镜引入了相位不连续的径向分布,分别产生球形波前和无衍射波前。Zhang 等[13] 设计了一种与 PB 相位灵活结合的透射式表面等离子超表面,实现了三维涡旋光束在宽带内的聚焦。另外,金属设计的单层超表面结构本身欧姆损耗较大,在实际应用中受到限制[14]。因此在利用几何相位设计超表面实现不同功能的同时,研究者们不断在组成超表面结构的高效率材料的选择上做研究。如 Chen等[15]设计了可见光和近红外波段的等离子体超构透镜,实现了正交圆偏 振光入射下的透镜正负工作模式。Khorasaninejad等[16]利用 TiO2在可见光波段上设计了高效的超表面聚焦和成像。同时基于手性相关的多波长、多焦点透镜的设计,研究者们成果颇丰。例如,Huang 等[17]利用几何相位原理和全息光谱算法,完成了宽带内手性相关复用全息的设计。Wen 等[18]设计了一种双功能超表面器件,当左旋圆偏振光入射时可以实现全息成像,当右旋圆偏振光入射时可以实现透镜聚焦。Zhang 等[19]设计了一种可以根据不同手性圆偏振光入射产生全息成像和涡旋光束的全新超表面结构。Tchoumakov等[20]提出了一种单材料三维电子 Veselago 透镜,可选择性聚焦特定手性的电子。
以上前人所研究和设计的基于几何相位调制的超表面都是局限于手性圆偏振光,目前对利用几何相位调控的线偏振聚焦领域的研究还比较匮乏。因此本文设计了一种基于几何相位的线偏振光聚焦的亚波长全介质超透镜,实现了高数值孔径及分辨率的聚焦,摆脱了传统设计中几何相位需要左、右旋圆偏振光的手性限制。本文介绍了该结构的模型及尺寸参数,并对该透镜的聚焦效果进行了论证。接着探究了各变量对聚焦特性的影响。本研究对微纳米光学设计及图像成像具有重要的参考价值。
1 理论与模型设计
几何相位的使用最早出现在微波系统中。印度拉曼研究所的 Pancharatnam教授研究表明,电磁波在偏振态转化的过程中会产生一个额外的相位[21-22]。
通过琼斯矩阵来描述电磁波在超表面中的传输和几何相位产生的过程[23-24]
式中: Ex;out 和 Ey;out 分别是电磁波 x 和 y 偏振的出射分量; Ex;in 和 Ey;in 分别是電磁波的 x 和 y 偏振的入射分量; Jξ为琼斯矩阵,可表示为
对于各向异性的超表面,区别于 x 轴与 y 轴,设其局域坐标系的主轴方向分别为 u 轴和 v 轴,坐标轴 u 轴与 x 轴的夹角为ξ。该局域坐标系下电磁波的琼斯矩阵可表示为
式中 tu和 tv都是局域坐标系里两个主轴的透射复振幅。
如果入射电磁波的偏振态为 x 偏振,由式(4)便能获得相应的输出
由式(5)可知,电磁波在入射至各向异性的超表面后,其出射的电磁波不仅含有原偏振态的电磁波,还有一个入射电磁波所不具备的带有正交偏振的电磁波分量,其振幅大小为(tu - tv)sinξcos ξ。
当各向异性超表面绕 z 轴旋转90°时,此时局域坐标系与 x 和 y 轴的夹角就变成了ξ+π/2,由式(5)可以得到 x 线偏振入射电磁波的输出电磁波为
此时,其正交偏振态电磁波的振幅大小与式(5)相等,相位相差了π(多一个负号)。对于偏振态为圆偏振的电磁波入射时,经各向异性的超表面后得到的输出电磁波表达式为[25-26]
其中σ=千1,正负分别代表了圆偏振的右旋偏振态和左旋偏振态。在偏振态为左旋或右旋的圆偏振电磁波入射至各向异性的超表面时,出射的电磁波不仅含有复振幅为(tu+tv)/2 p2的原偏振态电磁波,还存在新产生的复振幅为(tu - tv) e2iσξ/2 p2的正交偏振电磁波,其旋向正好与初始入射的圆偏振态旋向相反。同时,该正交偏振态的电磁波还额外存在一个大小为2σξ的相位,这种相位便是几何相位,即 Pancharatnam-Berry 相位(PB 相位)。
同理,对于反射型超表面,在局域坐标系内,对应于复振幅透射系数 tu和 tv ,便有复振幅反射系数 ru和 rv ,那么该电磁波的输出表达式可以写为[27]
指向角空间变化(ξ角度变化)的矩形柱或其互补结构是设计几何相位型超表面器件的典型单元结构。这种几何结构对于不同的偏振态都具有各向异性,即在各个方向上其复振幅透射系数 tu和 tv都不相等。因此,当偏振态为圆偏振的电磁波入射到各向异性结构表面时,由式(7)知,与几何结构相互作用后所透过的电磁波不仅含有主偏振态的电磁波,而且还产生了具有正交偏振态(旋向相反)的电磁波。并且正交偏振态的电磁波会产生与结构指向角ξ相关的相位突变,其相位突变值为2ξ(σ=1),即附加的额外相位是几何结构基于初态的旋转角度的两倍。
此外,为了使该超透镜像球形透镜一样工作,其相位轮廓需要遵循相位公式[28]
式中:φ(x;y)为单个纳米柱所提供的相位;x 与 y 代表了纳米柱的空间坐标值;λ为本文设计的入射波长; f 为理论的透镜焦距。
本超透镜的相位设计依赖于几何相位,即通过改变硅纳米柱的旋转角度θ, 以获得固定值为2θ的几何相位。联结式(9)得到单元结构的特定排布方式。
鉴于由介质硅材料组成的透射式超透镜拥有较高效的透射效率[29],因此其超透镜结构单元设为硅材料的矩形纳米柱,以有效保留较多的入射光波能量。如图1(a)、(b)所示是该超透镜的其中一个硅纳米柱结构单元侧视图和俯视图。其中,纳米柱单元结构的周期 S=325 nm ,硅(n =3.5)纳米柱的高度为 H1=600 nm ,宽度 W=95 nm ,长度 L =250 nm ,基底材料为二氧化硅。本文所设计的超透镜焦距为100?m,透镜半径为150?m,因此数值孔径 NA 约为0.83。由于硬件模拟设备条件的限制,本设计方案按比例缩小至纳米柱单元数为17×17的尺度进行数值模拟。此时,超透镜的设计焦距 f=1.5?m,透镜半径 R=2.7?m 。图1(c)为超透镜部分结构根据几何相位的原理进行排布的示意图。在设计选择结构尺寸之间,本文首先模拟扫描了在入射光下结构单元相位,接着选取合适的结构尺寸参数,以实现0~2π相位的全覆盖,如图2所示。
2 参数设置与仿真结果分析
为了计算出光波入射全介质超透镜后的聚焦效果,本文利用时域有限差分法(finite different time domain, FDTD)的数值模拟方法设计并优化超透镜的结构参数,使超透镜结构的光学功能与理论设计相符合,得到全介质超透镜结构的聚焦场强分布图,如图3所示。
该设计除了 z 平面外,在 x 平面和 y 平面的边界也设置了完美匹配层(PML)边界条件。在数值模拟中采用了可见光波段中波长为600 nm 的线偏振平面波,对全介质超透镜结构进行垂直入射,图3为超透镜入射与聚焦的示意图。与较小尺寸的滤光片孔径结构相比,本超透镜结构由于是由纳米柱组成的阵列结构,非单元结构仿真,所以在硬件模拟设备条件有限的情况下,数据精度设置较低(在满足仿真需要的情况下, FDTD 仿真网格精度取1,监视器取样点个数设置100)。
图4为 FDTD 模拟并归一化的全介质超透镜的电场强度分布图。图4(a)为 x-z 平面归一化后的电场强度分布图,图4(b)为焦点处 x-y 平面归一化后的电场强度分布图。从图中可以看出,电场的能量几乎全部聚于焦点处,这归因于单个硅材料纳米柱结构在600 nm处有较高的透射率,且没有散焦,保留了较高的电场能量。聚焦特性较好,实现了基于几何相位的线偏振光聚焦。
接着,本文分别对各场强分布进行了数值化处理,其曲线结果如图5所示。图5(a)为 z 轴方向电场强度分布数值图,图5(b)为焦点处的 y 轴电场强度分布数值图。从图中可以看出,超透镜很好地将线偏振平面波聚焦于 z 轴的1.5?m 处,半高全宽(FWHM)为334 nm,模拟的聚焦结果与本文所理论设计的焦距相吻合,摆脱了传统设计中基于几何相位的超透镜需要左右旋圆偏振入射光的手性限制。
3 各变量对聚焦特性影响的探究与验证
3.1 纳米柱材料的变化
本文首先探究了部分金属(金、银、铜)材料替代硅材料后,基于几何相位的超透镜的聚焦效果。图6(a)~(c)分别为金、银、铜3种材料的纳米柱阵列组成的超构透镜在垂直入射600 nm 线偏振平面波等参数不变的情况下的聚焦效果。可以清楚地看到,与硅纳米柱相比,这三种材料的纳米柱构成的超透镜聚焦于焦点处的电场强度明显降低(根据模拟数据显示,其聚焦能量分别约为硅纳米柱的37%、70%和50%)。
此外,图7给出了三种金属材料制成的超透镜的纵向(z 轴)电场强度曲线图。焦点处(右侧峰值处)从上到下分别为:银、铜、金,其焦距较大,偏离了理论设计的焦点位置(模拟结果比理论设计的焦距分别多了0.8?m 、0.5?m 以及0.7?m)。究其原因可能是由于光源入射到超透镜时发生欧姆损耗导致的,一部分出射光被削减,从而造成能量损耗,且金属制超透镜或于600 nm 的波长处没有产生较好的表面等离子体共振。
3.2 可见光波段的波长变化
接着,本文研究了在可见光波段的范围内,波长的变化对基于几何相位的全介质超透镜聚焦特性的影响。在保持全介质超透镜各尺寸参数不变的情况下,将400~700 nm 的可见光平面波波段以100 nm 为一个步长,对超透镜进行模拟,得到的聚焦效果如图8所示。接着对纵向(z 轴)的电场强度分布进行处理,其焦点变化曲线图如图9所示。
由图8和图9可以看出,随着入射光波长的增加,设计的全介质超透镜的焦距逐渐拉长,电场强度也相应减弱。这说明在相位式(9)的作用下,只有理论设计的入射光波长(本设计为600nm)能在焦点处聚集最大的电场能量,且模拟的焦距结果与理论分析一致。而其他波长的可见光虽然也能够实现聚焦,但会出现散焦现象,无论波长取何值都会造成部分能量损失,导致实际焦点处的电场强度明显低于理论设计的波长,同时焦距结果与理论误差也较大。这说明,根据式(9)所设计出的超透镜,最好用于理论设计波长的光源,否则在理论焦距处无法得到理想焦点,这可以应用于聚焦过程中的二次滤光。同时可以看出,实际模拟结果的焦距与波长呈负相关,表明该超透镜具有一定的负色散。虽然本文所设计的透镜在可见光波长范围内具有较好的聚焦效果,但仍然可以通过额外消色差设计更好地实現可见光波长范围内的消色差聚焦,从而完善超透镜的设计,更好地满足各类应用需求。
3.3 设计焦距的变化
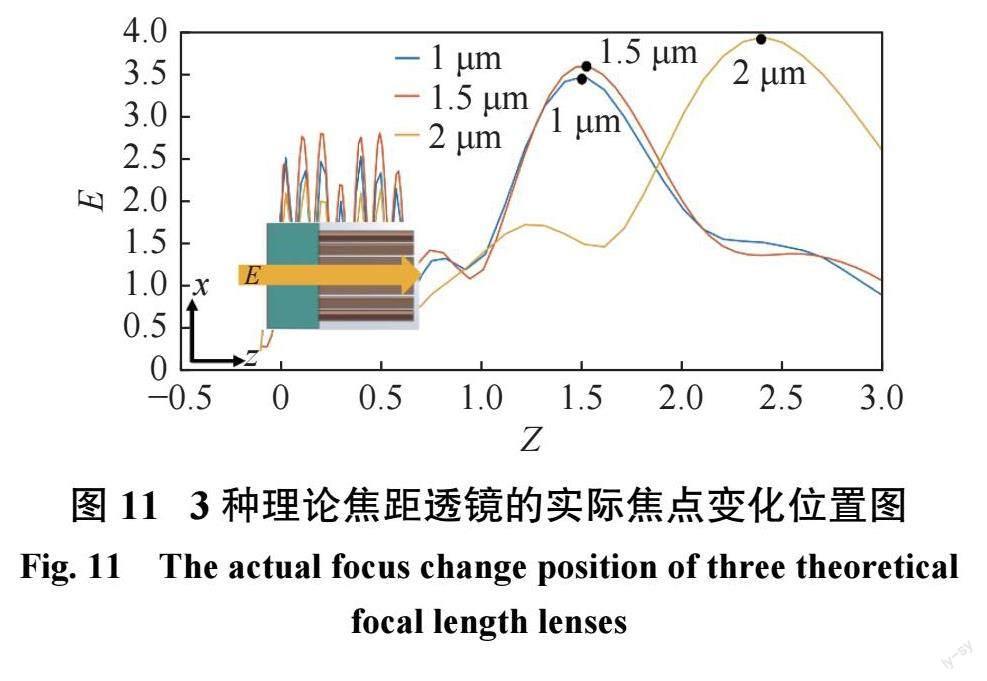
本文还探究了不同理论设计焦距与模拟结果之间的误差和电场强度变化。在设计尺寸参数和入射光波长不变的情况下,根据式(9),改变硅纳米柱的排布方式,得到不同理论设计焦距的超透镜。图10为理论设计焦距分别为1?m、1.5?m 和2?m 的全介质超透镜的聚焦效果。然后对纵向(z 轴)电场强度分布进行处理,得到的电场强度分布曲线图如图11所示。
从图10和图11中可以看出,随着理论设计焦距的增加,设计的全介质超透镜的焦距逐渐拉长。但是,除了1.5?m为理想焦距,理论焦距为1?m与2?m 的误差较大:在1?m处,焦点位置接近1.5?m;在2?m处,焦距误差约为0.4?m。改变理论焦距意味着改变数值孔径(NA),这也意味着改变超透镜的分辨率。因此,在设计超透镜时,数值孔径(NA)值确定后,理论焦距也随之确定,不应作为优化参数加以改变。
3.4 纳米柱的高度变化
最后,本文探究了硅纳米柱高度变化对全介质超透镜聚焦特性的影响。在设计的全介质超透镜长宽和焦距不变、入射光固定为波长600 nm 线偏振平面波的情况下,将纳米柱阵列的高度从100 nm 开始,并以100 nm 为一个步长,对高度从100 nm 至800 nm 的纳米柱阵列进行模拟。图12为纳米柱高度从100 nm 至800 nm 的全介质超透镜的聚焦效果。然后对纵向(z 轴)电场强度分布进行处理,得到的电场强度分布曲线图如图13所示。
从图12和图13中可以看出,随着硅纳米柱高度的增加,设计的全介质超透镜的焦距逐渐拉长。除了本文设计的600 nm 高度外,其余高度的模拟结果均偏离了理论焦距(1.5?m),并且出现了一些散焦现象,造成了部分能量损失。这证实了纳米柱高度对相位有着一定的影响,无法完美覆盖0~2π, 进而影响了出射光的波前,最终影响了超透镜的聚焦效果。
4 结 论
本文设计了一种基于几何相位的全介质超透镜,其与超表面滤光片主要输出波长一致,以配合研究滤光片的输出性能。借助几何相位原理,使该相位不受入射波长的影响,可以使超表面透镜工作在宽带上。将纳米柱阵列按照一定的规律均匀排列于二氧化硅的基底上,很好地实现了于可见光波段的波长为600 nm线偏振光在1.5?m 处的近场聚焦。摆脱了传统的设计中基于几何相位的超透镜需要左右旋圆偏振入射光的手性限制。
接着本文研究并验证了超透镜的材料、波长、设计焦距和高度等变量对光场聚焦特性的影响,这些研究将为今后的实验设计提供参考和基础。利用这种超透镜进行成像,它们可以产生亚波长分辨率,图像质量或可与商业透镜获得的图像质量相媲美。同时,这些器件在微纳光学、集成光学、成像、偏振检测等领域都有着广泛的应用。
參考文献:
[1] CHEN W T, ZHU A Y, KHORASANINEJAD M, etal. Immersion meta-lenses at visible wavelengthsfor nanoscale imaging[J]. Nano Letters, 2017, 17(5):3188–3194.
[2] FAN Z B, QIU H Y, ZHANG H L, et al. A broadbandachromatic metalens array for integral imaging in thevisible[J]. Light:Science & Applications, 2019, 8(1):67.
[3] ZHOU X M, ASSOUAR M B, OUDICH M. Acousticsuperfocusing by solid phononic crystals[J]. AppliedPhysics Letters, 2014, 105(23):233506.
[4] ADDOUCHE M, Al-LETHAWE M A, CHOUJAA A,et al. Superlensing effect for surface acoustic waves ina pillar-based phononic crystal with negative refractiveindex[J]. Applied Physics Letters, 2014, 105(2):023501.
[5] LI J, WANG Z, MA Y, et al. Design of high-resolutionnear-field focusing metasurface lens[J]. Journal ofElectromagnetic Waves and Applications, 2021,35(16):2115–2124.
[6] ALI H, NI H B, XU X. Near-UV luminescencetomography with an aperture-free meta superoscillatory lens for single molecule detection[J].Journal of the Optical Society of America A, 2020,37(4):621–628.
[7] TIAN Z C, GUO Y M, HU C Y, et al. Broadbandefficient focusing on-chip integrated nano-lens[J]. ActaPhysica Sinica, 2020, 69(24):244201.
[8] BERRY M V. Quantal phase factors accompanyingadiabatic changes[J]. Proceedings of the Royal SocietyA Mathematical, Physical and Engineering Sciences,1984, 392(1802):45–57.
[9] HASMAN E, KLEINER V, BIENER G, et al.Polarization dependent focusing lens by use ofquantized Pancharatnam-Berry phase diffractiveoptics[J]. Applied Physics Letters, 2003, 82(3):328–330.
[10] CHEN Y Z, ZHOU C X, LUO X G, et al. Structuredlens formed by a 2D square hole array in a metallicfilm[J]. Optics Letters, 2008, 33(7):753–755.
[11] KANG M, FENG T H, WANG H T, et al. Wave front engineering from an array of thin aperture antennas[J]. Optics Express, 2012, 20(14):15882–15890.
[12] AIETA F, GENEVET P, KATS M A, et al. Aberration- free ultrathin flat lenses and axicons at telecom wavelengths based on plasmonic metasurfaces[J]. Nano Letters, 2012, 12(9):4932–4936.
[13] ZHANG Y C, LIU W W, GAO J, et al. Generating focused 3D perfect vortex beams by plasmonic metasurfaces[J]. Advanced Optical Materials, 2018, 6(4):1701228.
[14] MONTICONE F, ESTAKHRI N M, AL? A. Full control of nanoscale optical transmission with a composite metascreen[J]. Physical Review Letters, 2013, 110(20):203903.
[15] CHEN X Z, HUANG L L, M?HLENBERND H, et al. Dual-polarity plasmonic metalens for visible light[J]. Nature Communications, 2012, 3:1198.
[16] KHORASANINEJAD M, CHEN W T, DEVLIN R C, et al. Metalenses at visible wavelengths: diffraction- limited focusing and subwavelength resolution imaging[J]. Science, 2016, 352(6290):1190–1194.
[17] HUANG L L, M?HLENBERND H, LI X W, et al. Broadband hybrid holographic multiplexing with geometric metasurfaces[J]. Advanced Materials, 2015, 27(41):6444–6449.
[18] WEN D D, CHEN S M, YUE F Y, et al. Metasurface device with helicity-dependent functionality[J]. Advanced Optical Materials, 2016, 4(2):321–327.
[19] ZHANG C M, YUE F Y, WEN D D, et al. Multichannel metasurface for simultaneous control of holograms and twisted light beams[J]. ACS Photonics, 2017, 4(8):1906–1912.
[20] TCHOUMAKOV S, CAYSSOL J, GRUSHIN A G. Three-dimensional chiral Veselago lensing[J]. PhysicalReview B, 2022, 105(7):075309.
[21] PANCHARATNAM S. Generalized theory ofinterference, and its applications[J]. Proceedings of theIndian Academy of Sciences-Section A, 1956, 44(5):247–262.
[22] BORN M, WOLF E. Principles of optics:electromagnetic theory of propagation, interference anddiffraction of light[M]. Oxford: Pergamon Press, 1980:188?189.
[23]李雄, 马晓亮, 罗先刚.超表面相位调控原理及应用[J].光电工程, 2017, 44(3):255–275.
[24] ELLENBOGEN T, SEO K, CROZIER K B. Chromaticplasmonic polarizers for active visible color filteringand polarimetry[J]. Nano Letters, 2012, 12(2):1026–1031.
[25] PU M B, LI X, MA X L, et al. Catenary optics forachromatic generation of perfect optical angularmomentum[J]. Science Advances, 2015, 1(9):e1500396.
[26] YU N F, GENEVET P, KATS M A, et al. Lightpropagation with phase discontinuities: generalizedlaws of reflection and refraction[J]. Science, 2011,334(6054):333–337.
[27] GIL J J, BERNABEU E. Obtainment of the polarizingand retardation parameters of a non-depolarizingoptical system from the polar decomposition of itsMueller matrix[J]. Optik, 1987, 76(2):67–71.
[28] BOMZON Z, BIENER G, KLEINER V, et al. Space-variant Pancharatnam-Berry phase optical elementswith computer-generated subwavelength gratings[J].Optics Letters, 2002, 27(13):1141–1143.
[29] ARBABI A, HORIE Y, BALL A J, et al.Subwavelength-thick lenses with high numericalapertures and large efficiency based on high-contrasttransmitarrays[J]. Nature Communications, 2015, 6:7069.
(编辑:张磊)

