基于夹逼准则高精度靶向研判电站锅炉效率的算法研究

申朋宇,乔明帅,刘建超,郝 杰,崔 冰,肖 键,李耀德

(1.保定电力职业技术学院 动力工程系,河北 保定 071051; 2.东北电力大学 研究生院,吉林 吉林 132000; 3.中国能源建设集团 华北电力试验研究院有限公司,天津 300171)

2020年9月,我国提出2030年实现“碳达峰”,2060年实现“碳中和”的目标愿景[1]。2021年10月,中共中央、国务院发布《关于完整准确全面贯彻新发展理念做好碳达峰碳中和工作的意见》,提出要统筹煤电发展和保供调峰,严控煤电装机规模,加快现役煤电机组节能升级和灵活性改造。提升煤电锅炉效率作为国内外研究者长期关注的重点领域,依然面临着重大挑战。经过多年发展,锅炉效率虽已有较大幅提升,但依然存在诸多问题[2-4],诸如:按照美国ASME和中国国家标准,一般采用反平衡法计算锅炉效率,需要化验单位对入炉煤质进行元素分析。受技术条件限制,国内外电厂一般只能进行工业分析用于指导燃料配比,难以准确计算锅炉效率。锅炉性能测试需要耗费大量的人力、物力,电厂一般只能在5年1次的大修期内,才会邀请专门试验单位进行锅炉性能测试。而日常能耗管理中,由于电厂无法获得准确的锅炉效率数据,不能通过实时调控机组运行状态,保证锅炉及其附属设备始终在高效率状态运行,造成能源大量浪费。另外,在新机组考核试验中,由于受地理、技术等条件限制,现场无法对锅炉状况进行摸底测试,造成机组实际运行状态偏离设计要求,最终结果会给电厂建设合同双方造成很大争议;尤其在中国援建的国外电厂中,此类争议往往导致中方经济损失巨大。开发一种精度满足要求的锅炉效率实时在线的预测、监控系统,可以有效解决以上问题。

在锅炉效率计算预测方面,国内外科研工作者取得了一定研究成果。Men Yiyu等[5]在带烟气再循环的热水锅炉系统中开展了锅炉效率在线预测实验,结果显示在线效率监控程序能基本反映热水锅炉的实时状态,但预测结果与实测结果存在一定量偏差。smail Ata等[6]在土耳其一热电厂开展锅炉效率性能试验,分析了主要辅机设备的效率,并指出损失最大的部位,为锅炉效率在线诊断提供了数据支持。Sajad Koochakinia等[7]在1台燃用天然气锅炉上开展了效率测试和优化工作,开发了数值计算程序,结果显示,由于环境和运行条件变化,锅炉热效率和效率各不相同,热效率从83%上升到 87%,效率从27% 上升到32%。此外,通过优化过量空气系数,热效率和效率分别提高了1.5% 和 3%。张平等[8]基于大数据统计学模型,开展了电厂锅炉能效在线和远程诊断研究,对提高火电机组运行效率有积极作用。赵一凡[9]根据大数据计算原理,在实时监测模型基础上,构建了遗传算法优化模型,用以实现锅炉高效低污染的燃烧运行。

上述锅炉效率相关研究均建立在锅炉试验基础上,试验成本高,无法实现锅炉效率的实时在线监测。针对这种情况,本文通过大数据统计分析得到锅炉效率计算经验公式,在不开展锅炉试验的前提下,利用电厂日常工业分析数据,实现对锅炉效率的高精度研判,为实现锅炉效率在线预测和自主寻优奠定基础。研究思路如下:①基于ASME和国标中锅炉效率计算方法——反平衡计算所得的锅炉效率即是燃料燃烧效率为基础,通过统计汇总大量锅炉效率实测数据,建立数据库;②采用不同煤种分区研判,拟合锅炉效率回归曲线和经验公式,建立研判因子和锅炉效率的函数关系;③在建立初步数学模型基础上,基于微分学极限思想,采用上、下限同时逼近的方法,提高数学模型计算精度;④在先期建立的大数据库中,截取部分无烟煤、烟煤、褐煤实测数据,验证数学模型的有效性。

1 特性分析与数学建模

1.1 煤质分类

本文提出的锅炉效率计算方法基于电厂常规工业分析,为使计算结果更精确,应根据《中国煤炭分类》GB/T 5751—2009对煤质进行分类,见表1[10]。

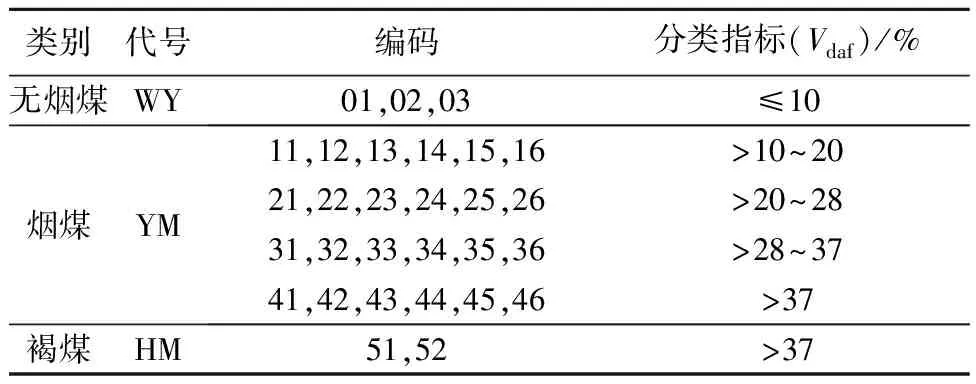
表1 无烟煤、烟煤及褐煤分类Tab.1 Classification of anthracite,bituminous and lignite coals

1.2 煤质判定因子的构建与解析

从工业分析的角度分析,煤的可燃性主要取决于煤质本身的挥发分含量(Vdaf),挥发分含量越高,煤化程度越低,煤质越疏松,越容易着火和燃烧;飞灰中的可燃物含量主要取决于煤的灰分(Adaf),灰分越低,烟气中飞灰颗粒越少,包覆在可燃颗粒(Cdaf)表面的概率越小、厚度越薄,煤的燃烬性越强。影响锅炉效率的第一要素是飞灰中的可燃物含量,而飞灰含碳量应同时考虑煤质中挥发分和灰分含量,基于上述燃烧理论,本文提出锅炉效率预测、判定因子(挥灰比),见式(1):

σi=Vdaf,i/Adaf,i

(1)

式中,σi为不同煤质的判定因子(挥灰比),i=1、2、3时,分别为无烟煤、烟煤、褐煤。

从式(1)可以分析得出,σi数值越大,煤的可燃特性和燃烬特性越好,飞灰中含碳量越少,亦即锅炉效率越高;但不同类型的煤,由于煤化程度不同,可燃特性和燃烬特性存在较大差别,仅采用上述判定因子预测锅炉效率会存在较大误差。本文根据文献[10]中提供的分类依据,搜集了以往大量不同炉型的电站锅炉性能试验测试结果(包括:煤粉炉、流化床炉、W火焰炉等炉型数据105种),建立了锅炉效率研判大数据库,并该通过大数据库拟合得到初步的锅炉效率预判经验公式,见式(2)—式(6)。

无烟煤:

η=3 318.556σ3-3 178.122σ2+982.619σ-5.281

(2)

烟煤:

σ=0.3～1.0时,η=-95.487σ3+176.22σ2-101.64σ+109.65

(3)

σ=1.0～1.2 时,η=97.932e-0.036σ

(4)

σ=1.2～1.8时,η=-57.547σ4+355.37σ3-813.12σ2-817.5σ+395.76

(5)

褐煤:

η=-18.423σ4+94.396σ3-176.04σ2+140.72σ+50.827

(6)

式中,η为无烟煤、烟煤、褐煤的初步预测锅炉效率。

采用数据库中小部分典型试验工况拟合得出的无烟煤、烟煤、褐煤判定因子与锅炉效率之间的关系如图1所示。

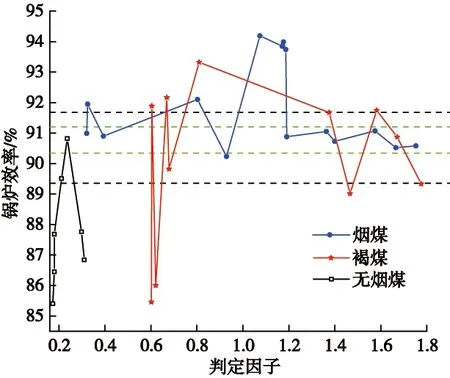
图1 煤质判定因子与锅炉效率之间的关系Fig.1 The relationship between coal quality determination factor and boiler efficiency

从图1中可以看出,无烟煤挥发分低,煤质可燃特性远低于其他煤种,灰分含量较大,导致其挥灰比较小;同时由于无烟煤煤化程度很高,煤质坚硬致密,可磨系数很小,煤粉细度通常比较粗,因而其燃烬特性较差,意味着飞灰颗粒中可燃物含量通常较高。燃用无烟煤的锅炉,热效率会低于其他煤种,一般比烟煤低3%～5%,比褐煤低3%～5%。根据GB/T 5751—2009,烟煤的分类区间很大,挥灰比变化范围也较大,但从图1中可以看出,燃用烟煤的锅炉效率波动区间却较小,多集中在90.4%～92.5%,为提高最终锅炉效率的预测精度,本文根据国标分类标准,将烟煤分段拟合了各区间预测公式。相对来说,褐煤的波动范围则较大,个别挥发分较低的褐煤,因煤中灰分含量很高,导致其燃烧效率比燃用无烟煤的锅炉效更低。总体来看,燃用褐煤的锅炉,热效率集中在89.0%～91.5%,通常比燃用烟煤低1个百分点左右。图1中,还可看出一个明显特征,无烟煤、烟煤和褐煤均存在一个最佳挥灰比区间。其中,无烟煤最佳挥灰比为0.24～0.28,烟煤为1.05～1.20,褐煤为0.8～1.0。通过数据库中的大量数据分析得出,挥灰比超越最佳区间通常是因为挥发分并没有明显上升,灰分减少较多,而固定碳含量几乎不变,意味着煤中水分含量会大幅度增大。水分含量增大,会导致燃烧器出口火焰延长,炉膛中的热量消耗增多,烟气量增大,炉膛出口的热损失增加;另一方面,水分越大干燥难度越大,一次风量会显著增加,空气预热器处带走的炉膛内热量显著增加,使锅炉效率降低。

在以往工程实践和研究文献中,对挥发分与燃烧效率之间的关系也多有涉及,煤中挥发分含量越高,燃烧效率越高是公认的观点,但大都停留在定性分析上,难以做到定量分析与预测[11-17]。本文采用新型计算方法,定量推导出了挥发分、灰分与燃烧效率之间对应关系,同时最佳挥灰比区间的提出和量化,为单一煤种燃烧优化以及多煤种掺混燃烧奠定了理论基础,对工程实践和科学研究有较强指导意义。

1.3 炉效预判数学模型的构建与解析

通过1.2节分析可知,不同煤种之间挥灰比相差较大,与挥灰比对应的锅炉效率也存在较大差值;但同一煤种如果分区间拟合研判公式,则预测精度较高,且数据量越大预测精度越高。烟煤典型区间σ为[1.2,1.8]时,锅炉效率研判数学模型解析(示例)如图2所示。点(1.45,90.97)是通过公式(5)计算出的炉效曲线计算值。为提高模型的预测精度,基于数学夹逼准则,锅炉效率预测值采用式(7)、式(8)进行第二次回归计算:

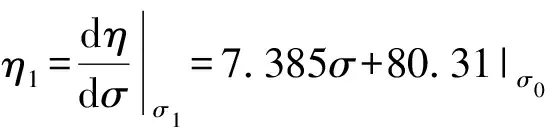
(7)

(8)

η=(η1+η0+η2)/3

(9)

式中,σ0为目标煤种的挥灰比(判定因子);η0为将σ0代入式(5)计算得到的锅炉效率;σ1为数据库中小于σ0且差值最小试验煤种挥灰比;σ2为数据库中大于σ0且差值最小试验煤种挥灰比;η1、η2分别为对式(5)求导计算得出的炉效;η为采用夹逼法则计算得到的锅炉效率。

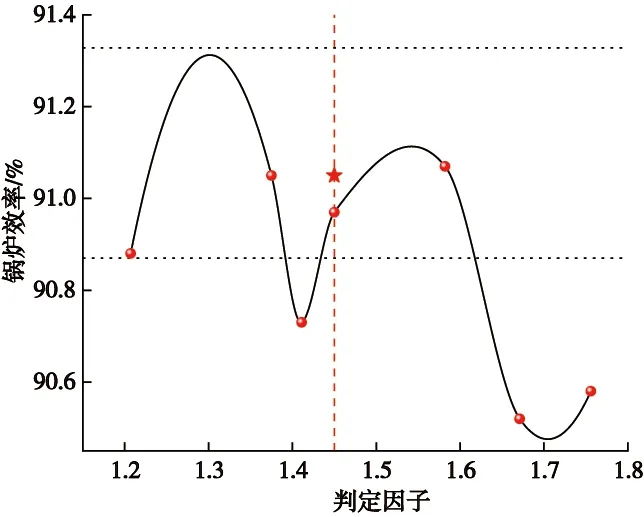
图2 锅炉效率研判数学模型解析(示例)Fig.2 Analysis of mathematical model for boiler efficiency evaluation(example)

其余煤种的锅炉效率预判均采用示例中的计算法则,对不同煤种、不同区间分别进行预测计算。

1.4 排烟温度、氧量修正

从图2可以看出,通过大量试验实测数据拟合得到的式(2)—式(6),可以对锅炉效率进行大数据模糊研判。但是实际中,由于受运行氧量、排烟温度、飞灰含碳量等因素影响,采用夹逼准则进行预测计算的锅炉效率与实测值存在一定的误差,需要对上述因素进行修正。通过1.2节中研判因子的分析可知,在大数据拟合的公式中已经考虑了飞灰含碳量的影响,且通过本文研究发现,采用挥灰比计算的锅炉效率与实测锅炉效率偏差在0.03%以内,能够满足课题研究和工程实际的要求,故本文不再对飞灰含碳量进行重复修正。

锅炉效率计算涉及到煤质成分、运行条件等诸多因素,各种因素之间也存在着相互作用16-17。为单独计算排烟温度、氧量对锅炉效率的影响,本文采用偏增量法对计算炉效进行修正。

根据《电站锅炉性能试验规程》(GB/T 10184—2015),锅炉效率一般采用反平衡计算,见公式(10):

ηb=100-(q2+q3+q4+q5+q6)

(10)

式中,ηb为锅炉效率;q2为排烟热损失;q3为气体未完全燃烧热损失;q4为固体未完全燃烧热损失;q5为散热损失;q6为灰渣物理热损失。

在锅炉各项损失中,排烟热损失占比最大,文献[4]中排烟热损失计算见公式(11):

(11)

V(O2)+V(N2)+V(CO2)+V(SO2)+V(CO)

(12)

式中,V(CO2)、V(SO2)、V(CO)、V(O2)、V(N2)、V(H2O)分别为1 kg收到基燃料不完全燃烧生成的CO2、SO2、CO的体积量,另外3种是烟气中剩余的O2、N2、H2O的体积量。

(13)

式中,Car、Mar、Har、Oar、Sar、Nar分别为1 kg收到基燃料中所含的C、H2O、H、O、S、N的质量分数;da为1 kg空气中的含湿量;α为过量空气系数。

由公式(10)、(11)可以推导出排烟损失全增量与偏增量之间的关系,见式(14):

(14)

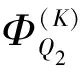
根据公式(14)可以推导出锅炉效率变化量,即排烟温度和氧量变化修正量,按照计算公式(15)进行计算。

(15)

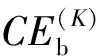
修正后的锅炉效率见式(16):

η=η+Δηb

(16)

式(10)—(13)中的所涉及到的元素分析成分含量(C、H、O、S、N)以及da等未知数可参考文献[5-8]计算得到,也可用本文课题组自主开发的,由煤质工业分析计算元素分析的高精度程序得出。锅炉效率测试中的燃料偏差修正、环境参数修正等可采用《电站锅炉性能试验规程》(GB 10184—2015)提供的方法计算,也可以采用锅炉生产单位提供的修正曲线计算,由于篇幅所限,本文不再赘述。

2 算例分析

2.1 无烟煤算例分析

无烟煤算例验证见表2,表2中仅列出3组预测结果及计算过程。

可以看出,如仅采用常规的实验数据拟合得到经验公式来预测实验结果,计算结果与实际测试结果将会存在较大误差。其中,第1组和第3组的曲线计算结果与预测结果偏差值分别为0.183%和1.17%,而第2组曲线预测结果已经出现失真现象。这是因为,在数据库中第1组和第3组的目标煤种挥灰比前后的试验数据较为密集,曲线拟合更为准确,而第2组目标煤种挥灰比前后的试验数据较少,回归曲线误差很大,R2仅能达到0.549左右。

从表2中还可看出,采用本文提出的导数夹逼准则,数学模型的预测精度有很大提高。第1组和第3组分别提升了0.141%和1.07%,达到0.042%和-0.1%,第2组预测精度也达到了0.121%,满足工程和科研需求,且随着大数据库中试验数据量的增加,采用夹逼准则靶向研判法,计算得到的锅炉效率与实际结果偏差会越来越小。

2.2 褐煤算例分析

通过数据拟合回归曲线及经验公式计算得出的褐煤锅炉效率与实测效率重合度分析如图3所示。

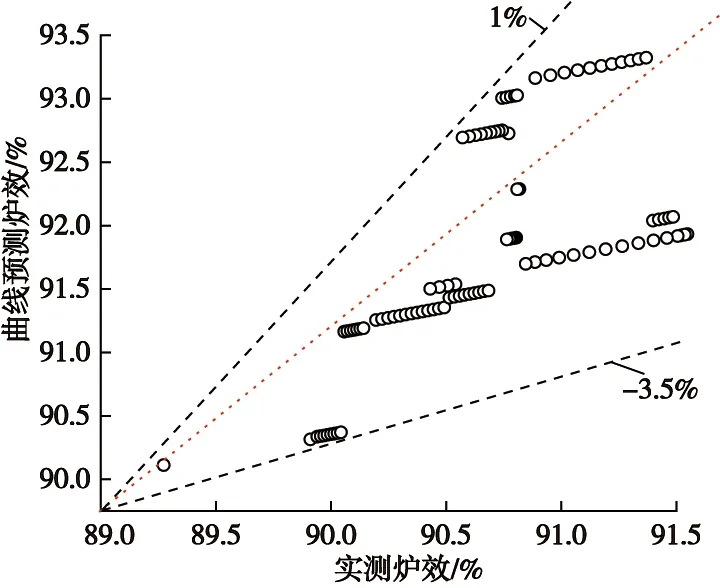
图3 褐煤的曲线预测炉效与实测炉效重合度对比Fig.3 Comparison of the coincidence degree between the predicted boiler efficiency of the lignite curves and the measured boiler efficiency

从图3中可以看出,仅通过回归曲线计算的锅炉效率与实测锅炉效率偏差很大,一般达到3.5%以上,难以用于指导工程实践。主要原因在于,数据库中实测数据不可能达到极高的密集度,导致曲线回归计算时部分失真。在数据点密集的区间内,个别点的回归计算结果能够满足科研精度要求,但在大部分区间内,经验公式的计算结果不确定度很大,这是以往研究中通常采用的实验数据先进行回归分析,得出经验公式后,再预测对象整体变化规律,这一研究方法的通病,很难彻底解决。

在回归曲线基础上,采用夹逼准则优化后计算得到的锅炉效率与实测锅炉效率重合度分析如图4所示。可以看出,预测结果与实测结果偏差已经大幅减小,最大偏差也仅0.1%。随着数据库中实测数据的充实,采用优化后的计算方法预测结果不确定度还会进一步减小。

图4 褐煤的夹逼准则预测炉效与实测炉效重合度对比Fig.4 Comparison of the coincidence degree between the predicted boiler efficiency and the measured boiler efficiency based on the clamping criterion

本文提出的优化方法特征在于,首先搜集大量实测数据进行回归分析,拟合得到一定精度的经验公式;然后在距离目标煤种判定因子最近的下限和上限实验数据处,分别进行求导计算,在无限小的范围获得和上限、下限实验数据同一斜率的函数值变化范围,此时就可以用直线变化率代替曲线变化率,分别计算出上、下限同斜率直线预测结果后,再与原曲线计算值进行均值计算,从而使预测结果尽可能落在与实测结果偏差最小的范围内,从而提高预测精度。从图3和图4中褐煤的预测计算来看,以上目的已达到。

2.3 烟煤算例分析

烟煤通过数据拟合回归曲线及经验公式计算得出的锅炉效率与实测锅炉效率重合度分析如图5所示。结合表1可以看出,烟煤的划分范围很广,在该大类中根据挥发分的大小还分可为4个亚种,在采用研判因子来划分曲线作用区间时,也体现出了上述特征,也证明了采用不同区间分段拟合经验公式可以一定程度上提高预测结果的精度,在图3中显示分段曲线的精度可以达到3%以内,这距工程实际要求相差依然较远,更不符合科研中的不确定度要求。

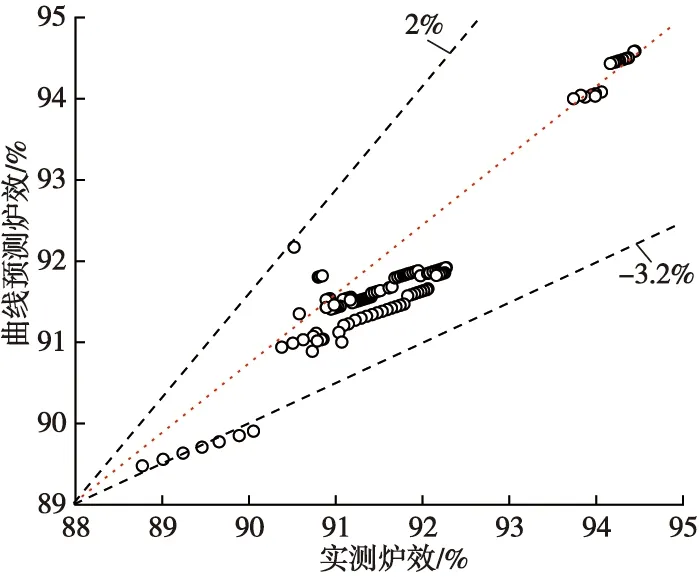
图5 烟煤的曲线预测炉效与实测炉效重合度对比Fig.5 Comparison of the coincidence degree between the predicted boiler efficiency of the bitumite curves and the measured boiler efficiency

在回归曲线基础上,采用夹逼准则优化后计算得到的锅炉效率与实测锅炉效率重合度分析如图6所示。可以看出,预测结果与实测结果偏差大幅减小,最大偏差也仅0.08%左右,说明采用分区间拟合经验公式,辅之以导数夹逼准则,最终结果的精确度有了大幅提升。

图6 烟煤的夹逼准则预测炉效与实测 炉效重合度对比Fig.6 Comparison of the coincidence degree between the predicted boiler efficiency and the measured boiler efficiency based on the clamping criterion

3 结论

(1)搜集以往不同电厂的锅炉效率试验实测数据,建立了数据库。基于大数据模型研判思想,提出了基于历史数据的电站锅炉效率预测模型,从新的角度对电站锅炉效率进行预测计算。该模型可以与机组现有的DCS系统相结合,对锅炉效率进行准确在线预测和实时跟踪,并能够实现自主寻优。

(2)基于ASME和国标中的锅炉效率反平衡计算法则,以煤质特性来表征燃料的燃烧效率,根据工业分析中挥发分和灰分含量,对煤的可燃特性和燃烬特性的关键影响,建立了研判因子(挥灰比)与锅炉效率的函数关系,拟合出了不同煤种的锅炉效率经验公式,避免了用元素分析计算锅炉效率的局限,可节省大量人力和时间成本。

(3)在以往研究中,研究人员通常采用实验数据拟合出经验公式,从而预测出研究对象的宏观变化规律。由于实验数据量和回归方式的局限,这一研究方法往往预测精度不高。本文以微分学极限分析思想——在无限小的范围内可以用切线变化量来代替曲线变化量为出发点,对距离目标煤种研判因子最近的上、下限实测炉效曲线分别进行求导后,再结合曲线本身的计算结果进行均值计算,实现无限逼近,可大幅提高回归曲线的预测精度。

(4)预测结果和实测结果对比分析表明,基于夹逼准则优化后的数学模型,预测精度有了明显提高,无烟煤、烟煤、褐煤等煤种的研判精度均已达到0.1%以内,满足科研和工程实际的要求,为通过DCS系统对锅炉效率进行实时控制和在线寻优奠定了理论基础。