考虑货物时间价值的国际集装箱多式联运路径优化
吴晓黎,寇 淇*,汪泳波
(1. 华南理工大学 工商管理学院,广东 广州 510640;2.华南理工大学 电子商务系,广东 广州 510006;3. 深圳市中海通物流股份有限公司,广东 深圳 518000)
0 引言
随着全球经济和贸易的不断融合,跨国运输联系日益频繁,多式联运作为一种现代化的运输组织方式,能够最大限度地发挥各种运输方式的优势,从而实现更高效的资源利用、更长的运输全程距离以及更好的综合效益。近年来,新冠疫情的爆发为当前国际集装箱运输带来了更大的机遇和挑战。一方面,订单和运量暴增,国际集装箱运输价格上升到之前的数倍甚至十倍;另一方面,由于疫情管控与工人停工等造成国际集装箱运输的时效延长,普遍存在延时问题。国务院也提出要大力发展多式联运,优化运输结构,提升运输效率,降低运输成本[1]。因此,在运输路径选择中,如何同时实现成本和时效两个方面的最优化,是一个迫切需要解决的难题。
随着研究的不断深入,部分学者也探究了多目标规划问题。Topaloglu等[15]针对运输过程中的车队管理问题,结合相关算法建立了综合模型。Ayed等[16-17]综合各方面因素构建了多式联运路径选择模型,旨在有效解决城市道路拥堵问题。Ayar等[18]针对海铁联运方面存在的问题,构建了多目标最优路径规划模型,以便控制运输成本和减少滞港时间。Cho等[19]构建了WCSPP模型,该模型通过双目标动态规划算法的应用可以实现成本和时间的双重兼顾。Ben-Akiva等[20]以客流预测为研究内容,构建了Logit模型,同时在货运量预测方面构建了ADA模型。上述模型在很多国家进行了应用并取得良好效果,其有效性得到证明。Barceló等[21]以时间作为目标函数,通过构建实时决策模型来提升城市货流分配效率,旨在有效解决货流分配方面存在的问题。张敏等[22]将运输成本、碳排放成本和客户满意度作为目标函数,通过多目标规划研究了低碳多式联运问题。上述多目标规划研究均未考虑货物时间价值,集装箱箱型等因素,而本研究构建的双目标优化模型考虑了上述因素的影响。并且,为了更好地解决多式联运问题,本研究也改进了传统Dijkstra算法。
综上,随着多式联运的快速发展,国内外学者都进行了一系列深入研究。现阶段的多式联运路径规划模型,包括单目标模型和多目标模型。单目标规划模型常见的目标函数包括路程最短化,成本最小化等等。多目标规划模型则包括两种常见模式:第1种是目标权重约束设计;第2种是目标权重求解。但是就现阶段而言,对国际集装箱多式联运的多目标规划模型的研究较少。随着全球经济化的发展,国际货物运输需求逐年递增,市场主体对货物运输方案的要求以及运输企业的服务水平也逐渐提高[23]。而本研究以国际物流运输为研究对象,对国际集装箱多式联运最优路径规划进行研究。本研究的创新之处主要体现在以下两个方面:(1)在国际集装箱多式联运模型设计中考虑最小运输成本、最小运输时效两个目标规划模型,并采用权重分配将其转化为单目标规模型,更有现实价值。其中,最小运输成本模型在传统基础上考虑了相对微观的决策影响因素,如箱型、多式联运中转时间、多式联运等待时间等;(2)在模型求解算法上,为了让传统Dijkstra算法更好地解决多式联运问题,从3个方面对其进行改进:考虑有向带权的连通图,循环多顶点标号,增加交通工具类型元素。
1 模型描述
1.1 问题描述
探究国际集装箱运输最优路径规划问题,问题可用已知的源G=(V,E,W,T)来表示。其中,V为国际集装箱多式联运过程中的节点组合,包含运输起点、运输中点和运输终点。E为节点之间的运行方向。W为两两节点组成的权值,传统权值主要是线路长短,由于研究对象为多式联运的最优路径规划问题,因此权值为多目标规模模型的求解结果。T则为运输交通工具类型,即两两节点组成的线段所需的交通工具类型。
1.2 研究假设
具体假设如下所示:
(1)各个节点换装最多只有一次。多式联运下的货物运输节点可以选择换装或者不换装两种决策,但换装之后会确定相应转运方式。
(2)运量不可细分,具有整体性。多式联运下的货物是统一整体,不可将其划分成不同批次进行独立运输。
(3)运输路线不能改变,具有固定性。另外,运输速度和单位成本也具有固定性。
(4)运输过程集装箱的适配性。多式联运下的集装箱均采用国际标准,不存在所谓适配问题。
(5)排除外部意外因素的影响。例如交通拥堵、天气恶化等因素。
(6)节点之间运费的稳定性。多式联运下节点的运输费用,不考虑淡旺季浮动的影响。
1.3 符号说明
使用到的符号及其具体含义如下所示:
决策变量:
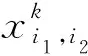
其他变量:
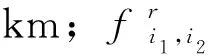
2 模型构建
2.1 运输成本节约模型
从节点i1到节点i2的国际集装箱多式联运的运输成本如式(1)所示:
(1)
式(1)为从节点i1到节点i2的运输成本主要由集装箱使用费、运输费、中转费这3部分组成。
其中,集装箱使用费计算如式(2)所示:
(2)
集装箱运输费用计算如式(3)所示:
(3)
集装箱中转费用计算如式(4)所示:
(4)
因此,从起点O到终点D的国际集装箱多式联运运输的总成本Z如式(5)所示:
(5)
需要满足如下的约束条件:
(6)
N1q1+N2q2≥Q,
(7)
(8)
(9)
N=N1+N2,
(10)
k,l∈{1,2,3,4},
(11)
(12)
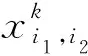
2.2 最短运输时间模型
从节点i1到节点i2的运输时间如式(13)所示:
(13)
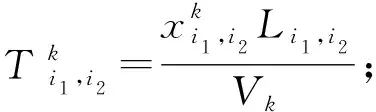
因此,从起点O到终点D的运输总时间T如式(14)所示:
(14)
式(14)需要满足如下的约束条件:
(15)
(16)
(17)
(18)
T≤Tmax。
(19)
其中,式(15)~(18)与模型2.1中的约束条件有着相同的含义,在此不再赘述。式(19)为运输时间要小于客户所能承受的最大范围。
2.3 货物时间价值模型
周伟[24]认为将成本模型与效率模型通过权重设计转化为单目标函数,需将效率模型与成本模型的单位统一。因此,将引入货物时间价值函数,实现集装箱多式联运运输时间模型向货物时间价值模型的转换,进而得出最优解,确定最优路径。
为降低研究难度,本研究选择线性函数展开研究。考虑到货物运输持续时间不会过长,且货物生命周期有限,因此本研究以月贬值率为指标。那么货物时间价值函数具体如式(20)所示:
(20)
式中,Pmax为货物最开始运输时(T=0),单位集装箱的运输价值;η和k分别为货物的入箱率和货物月贬值率。
2.4 双目标优化模型
由于运输成本与运输时间本身之间存在着矛盾。通常运输时间越短,运输成本则越高,如何平衡二者关系是本研究需要探究的主要问题。在此,通过线性加权法将双目标转化为单目标,以此确保规划模型的可解性。即根据不同类型客户需求偏好灵活设计子目标模型权重,继而求解模型最优解。
P=αC+βP(T),
(21)
式中,α为成本偏好系数;β为时间偏好系数。
具体的双目标优化函数如式(22)~(23)所示:
(22)
P(T)=
(23)
双目标优化模型下的约束条件与模型2.1和2.2中的约束条件相同,即式(6)~(12)以及式(15)~(19),在此不再赘述。
3 算法设计
求解“最短路径”的算法有很多,其中比较常见的算法包括Dijkstra算法,Bellman-Fold算法,SPFA算法,Johnson算法等等。本研究主要采用Dijkstra精确算法求解最优路径。
3.1 传统Dijkstra算法
最优路径规划模型涵盖两个基本要素:运输成本与运输效率。王涛等[25]借助时间价值函数与权重系数实现了多目标向单目标的转换。本节算法设计立足国际集装箱,多式联运实际。在Dijkstra算法实际应用中,需要输入的参数涵盖了基本查询条件,比如:始发站、终点站以及出发时间。因此,研究可选择精确串行算法中的Dijkstra算法作为本研究模型求解算法。
Dijkstra在最短路径确认方面提出了标号法,该方法也是现阶段被学者广泛认可的一种算法。该算法主要是针对权图中最短路径问题而采取的算法,可以确定某一顶点到其他各与顶点之间的最短路径。标号法目前在很多领域都得到非常广泛的应用,无论是在物流运输,还是在科学测绘等方面都取得良好成果。例如在高速公路收费、智能运输系统应用等方面利用标号法实现了有效突破,在确定最短路径方面发挥了重要作用。因此,很多学者开始探究基于Dijkstra的标号法,通过对这一算法进行优化和改进来更高效的探究最优路径。
相较于其他类型算法,Dijkstra算法的最大优势是应用了标号法。设G=(V,E,W),该式中V为所有顶点的集合,E为两两顶点之间形成的路径,W为路径对应的权重系数集合。Wij是大于等于0的数值,当i与j出现不相邻的情况,那么可出现Wij=∞。而Dijkstra算法的主要使用范围是对图G中任意两两节点之间的最短距离进行求解。
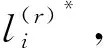
3.2 Dijkstra改进算法
3.2.1 Dijkstra算法的局限性
(1)尚未建立完善的算法退出机制。在一些有向带权联通图中,原有的Dijkstra算法并不具备可行性。
(2)无法满足多式联运过程中多个顶点可同时获得p标号的需求。
(3)无法满足多式联运交通工具多样性需求。本研究将多式联运作为研究对象,有向带权交通图涵盖了节点、方向、权以及交通工具类型k,所以该算法难以针对交通工具组合,选择提供有效的解决之道。
3.2.2 Dijkstra改进算法的符号设置
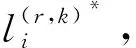

(3)假定Pr={v|v为已获得永久性p标号的顶点},那么标志着第r步通过集,r是大于等于0的数值;
(4)假定Tr=V-Pr,Tr标志着第r步的未通过集。
(5)假定Nr为第r步获取永久性p标号的点集合。
3.2.3 Dijkstra算法的改进原理
针对传统Dijkstra算法无法满足多式联运路径规划的局限性,提出以下改进思路:
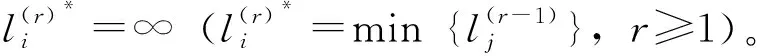
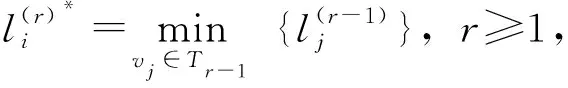
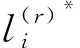
3.2.4 Dijkstra改进算法的求解步骤
本研究对传统Dijkstra算法进行改进之后,其计算过程主要包括3个步骤:
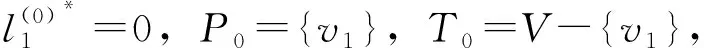
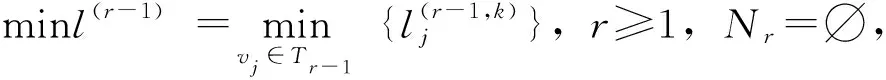
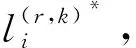
4 算例分析
4.1 算例数据
本研究选取了某公司由湖南C运往德国H的集装箱货物需求为案例场景,探究某公司多式联运通道的最优选择问题。具体描述如下:目前,某客户的货物需求为电子类产品,共计20个40尺普高箱和30个20尺开顶箱,共50箱货物,由C运往H,可供选择的多式联运通道为华南至西北大通道、华南至中部各省份城市,与国际大通道海运或中欧班列等的结合。具体的运输路径如表1所述。
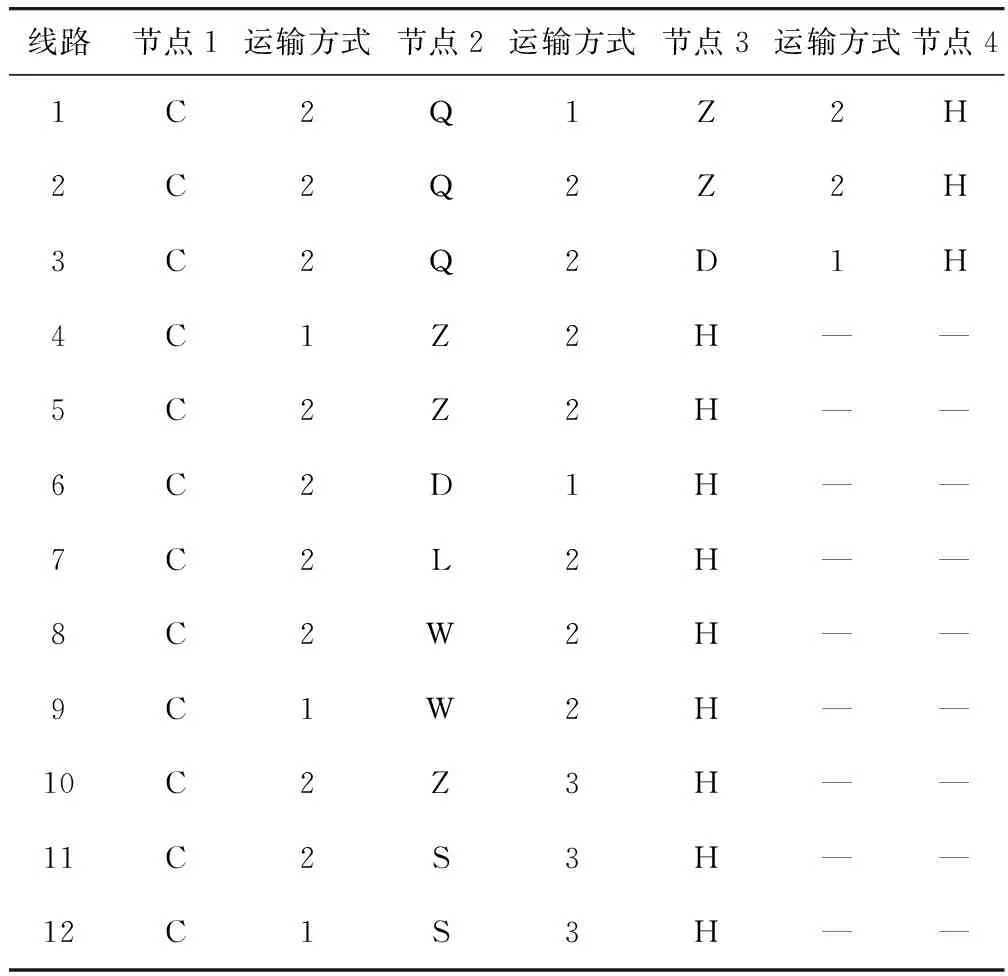
表1 湖南C市运往德国H市的集装箱运输路径Tab.1 Container transport paths from city C in Hunan to city H in Germany
除此之外,还需搜集不同交通工具的运输速度、节点之间不同交通方式的运输距离以及运输费用等。相关数据见表2。
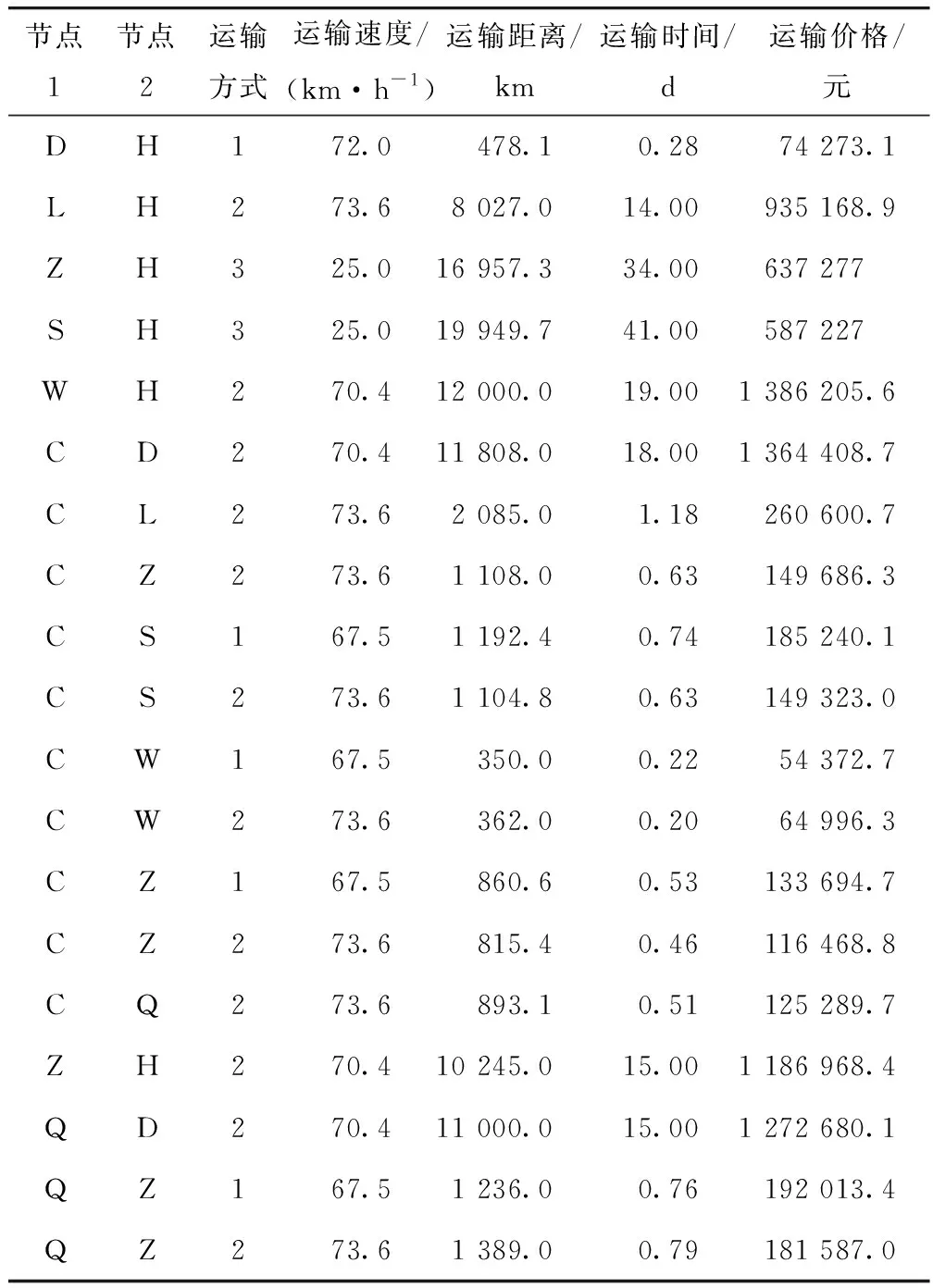
表2 各节点之间的相关运输数据Tab.2 Relevant transportation data among nodes
4.2 模型求解及结果分析
基于搜集的模型指标数据,赋予成本模型与效率模型不同权重,求解单目标综合模型的求解结果。从极端值与均值两个角度,分别进行权重设计试验,求解不同权重需求下,国际集装箱运输的最优路径,具体求解结果可见表3。
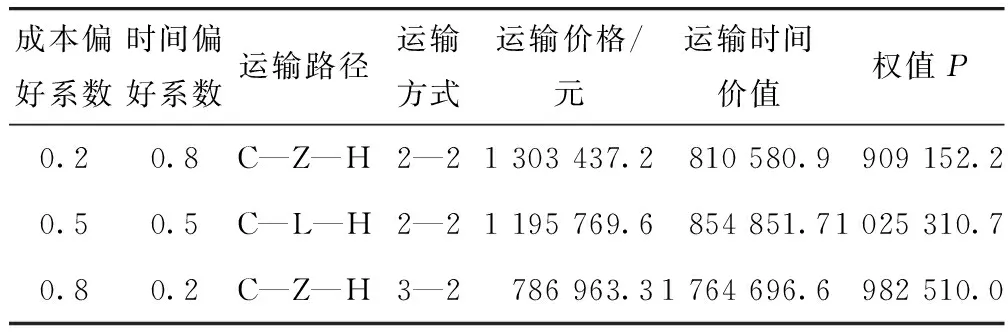
表3 多式联运最优路径方案Tab.3 Optimal path program of multimodal transport
当成本偏好系数为α=0.2,时间偏好系数为β=0.8,该类型客户为运输时间偏好型客户,即客户希望运输时间最短。最优路径为“C—Z—H”,该路径下的运输长度P=909 152.2,运输成本为C=1 303 437.2。
当成本偏好系数为α=0.5,时间偏好系数为β=0.5。该类型顾客会综合考虑运输时间和运输成本,此时,最优路径为“C—L—H”,该路径的长度为P=1 025 310.7,运输成本为C=11 957 690.6。
当成本偏好系数为:α=0.8,时间偏好系数为:β=0.2,该类型客户为运输成本偏好型客户,即希望运输成本最小。在此需求下,最优路径为“C—Z—H”,该路径的长度和成本分别为P=982 510.0和C=786 963.3。
综上,本研究构建的国际集装箱多式联运最优路径规划模型与算法,可为不同运输目标型客户,提供不同的最优运输方案,能够满足不同类型客户差异化需求,提升运输效率,建立与客户的良好关系。
4.3 最优路径对年度运输总量的影响
对客户而言,除了关注当次的运输成本、运输时间外,也关注路径规划对年度运输总量的影响,接下来,主要讨论这3种路径规划对年度运输总量的影响。
由表4可以得出,“C—L—H”,“C—Z—H”这两个路径下,年度运输总量相差不大,但“C—L—H”路径的成本较低;而“C—Z—H”这个路径虽然成本较低,但年度运输总量下降明显,因此,在综合考虑成本、时间以及年度运输总量的情况下,“C—L—H”是最优路径。
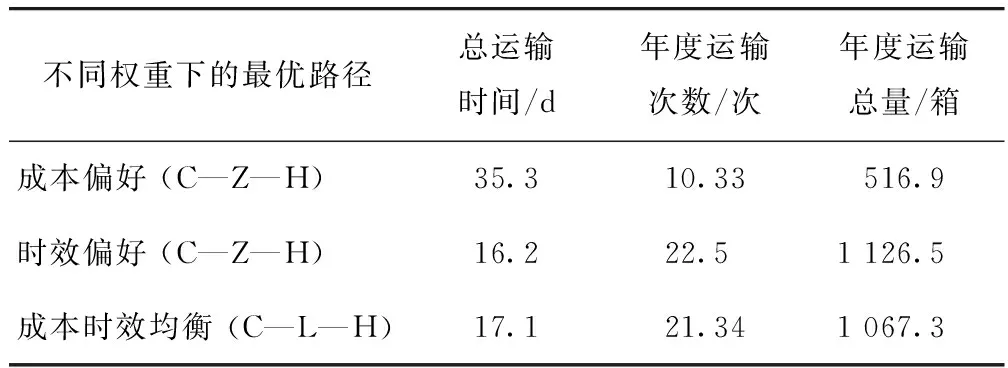
表4 不同最优路径下年度运输总量Tab.4 Total annual transportation with different optimal paths
4.4 改进Dijkstra算法的检验
为了验证本研究构建的Dijkstra改进算法模型在解决多式联运问题中的有效性,本节将引入启发式算法对上述案例进行求解。然后,将这3种不同需求下Dijkstra改进算法模型与混合算法模型的结果进行对比分析。
4.4.1 启发式算法及求解
考虑前文构建的Dijkstra改进算法模型在时间、成本方面进行了权重分配对比,因此,在混合算法的迭代中,也加入了这一因素,分别进行了3次迭代:对成本重视程度较高、对时间重视程度较高、时间成本均衡,关键参数设置为:种群数量为100,选择概率为0.01,变异概率为0.15,信息素初始值为10。表5给出了3种不同需求偏好下的求解结果,从仿真结果可以看出,3种不同需求偏好求解问题的最终结果差异较大,但时间成本均衡下具有更快的收敛能力。

表5 不同需求偏好结果比较Tab.5 Comparison of results from different demand preferences
4.4.2 算法对比
将Dijkstra改进算法模型与混合算法模型结果进行对比见表6。可以发现,相对于混合算法而言,改进Dijkstra算法求解效果要略微优秀,在这3种需求下,总时间均比较小。成本方面,只有对成本偏好较高 (α=0.8,β=0.2)时,混合算法成本略低于Dijkstra改进算法,其他两种情况,混合算法都是高于Dijkstra算法的,特别是时间成本均衡的情况下,差值相对较大,而这种情况是客户需求做多的情况,充分验证了本研究构建的Dijkstra改进算法模型在解决多式联运问题中的有效性。

表6 Dijkstra改进算法与混合算法结果比较Tab.6 Comparison of results between improved Dijkstra algorithm and hybrid algorithm
5 结论
本研究在考虑货物时间价值,集装箱箱型等因素的条件下,研究集装箱多式联运问题,依次建立运输节约成本、最短运输时间模型,以及整合运输成本和时间加权的双目标优化模型,并对传统的Dijkstra算法进行改进。利用ZH公司的实际案例数据进行算例分析,验证构建的双目标优化模型和求解算法的可行性和有效性,并进一步地探究最优路径对年度运输总量的影响。研究结果表明:(1)不同运输目标客户的需求偏好会影响多式联运最优路径的选择,进而影响运输成本、运输时效及年度运输总量。(2)与混合算法相比,Dijkstra改进算法求解效果更优。只有对成本更加偏好时,混合算法在解决多式联运问题时的成本略低于Dijkstra改进算法,而在其他情况下,Dijkstra改进算法求解出的运输成本和时间则更加经济高效,其最大时间节约率和成本节约率分别为30.86%,20.31%。
不足与展望:受限于各方面因素,本研究依然存在不足之处。例如,多式联运过程中不同交通工具的发车时间、作业时间带有一定的预估性,与实际存在一定偏差,实际上不同交通运输方式会有专门的列车时刻表,因此,未来可将列车时刻表与模型算法共同导入智慧系统,实现对国际集装箱多式联运的智能选择。

