涡轮增压器瞬态切换过程轴向力变化规律研究

王亚明,李晓杰,董小瑞,王 军,韩 啸

(中北大学 能源与动力工程学院,太原 030051)

0 引言

增压器叶轮在高速旋转时,气体的旋转和叶片两侧压差导致涡轮增压器轴向载荷的形成。轴向力在一定程度上会影响其寿命、性能和整个系统的可靠性[1]。增压器轴向力由压气机端轴向气动力与涡轮端轴向气动力两部分组成,其承载部件是止推轴承[2]。由于增压器的结构特性和工作环境因素影响,直接测量涡轮增压器的轴向推力比较困难,或者即使直接测试也无法反映涡轮轴向力的真实情况[3-4]。增压器轴向力计算方法参考文献[5]。

关于增压器工作过程轴向力的研究中,Lee等[6]提出了涡轮增压器在工作过程中的轴向力预测方法,预测结果能与有限元仿真结果很好地吻合,为进一步准确预测轴向力提供了依据;张海磊等[7]分析了理论轴向力值与数值计算结果之间的误差,为轴向力预测提供了参考,并探究了稳态下同一转速与流量和密封环间隙对于轴向力的影响;洪汉池等[8]采用在止推轴承上粘贴应变片的方法测量增压器在启停过程中的轴向力,发现启停过程中轴向力远大于稳定工作时;Zhang等[9]提出了一种预测增压器工作状态下的轴向力的方法,同时研究了增压器发生故障的条件;房桐毅等[10]探究了篦齿对增压器轴向力的影响;王翠翠等[11]通过一种悬浮式设计的轴向力测试方法研究了转速与质量流量对增压器轴向力的影响;李伟等[12]通过CFX软件仿真研究了相继增压系统切换过程中小增压器轴向力的变化,通过分析内部流场发现轴向力合力主要源于压端,在切换过程中流场发展得较流畅,涡端的叶根与叶片处出现涡流。张健健等[13]研究了不同油楔面的油膜厚度,探究止推轴承的承载能力,同时通过仿真发现轴向力随转速升高而增大。杨豫魁等[14]探究了发动机运行工况下,发动机转速变化和负荷阶跃时的增压器轴向力的变化规律,发现发动机负荷阶跃时间越短,轴向载荷越大。

相继增压系统在运行过程中处于频繁的切换工况[15]。本研究以相继增压系统单增压模式切换为双增压模式过程中的基本增压器为研究对象,此时阀门开启,通过基本增压器的废气量减少、转速下降,待两增压器运行平稳后完成切换。建立增压器压气机与涡轮机的三维模型,采用Fluent对压气机、涡轮机流场进行数值仿真。前述文献大多研究整个切换过程中轴向力的变化趋势或稳态情况下的轴向力,其中启停工况属于瞬态过程,属于少数工况;相继增压系统大部分时间处于频繁切换工况,且切换工况下压气机易发生喘振等恶劣情况,增压器轴向力变化剧烈,容易发生损坏,因此以切换瞬态轴向力变化情况为重点,在阀门开启、增压器工作环境不断变化时,观察轴向力的变化规律和相应的形成机理,为增压器的止推轴承设计和切换过程的阀门控制动作提供理论依据。

1 模型建立

采用数值模拟的方法研究轴向力。取压气机指向涡轮机为正方向,其轴向受力如图1所示。针对相继增压器系统的基本增压器进行研究,选用某型增压器,压气机叶轮直径为75 mm、涡轮直径为59 mm。在Fluent Meshing环境下划分网格,涡轮增压器计算域网格如图2所示。

图1 涡轮增压器轴向载荷示意图

为保证计算效率的同时获得高质量的CFD结果,分别绘制涡轮机与压气机5套网格。涡轮机的网格方案为:60万、100万、180万、230万、280万;压气机的网格方案为:80万、132万、184万、254万、346万。

依据边界层理论,由于边界层的厚度比物面特征尺寸小得多,在运用纳维-斯托克斯方程进行逐项数量级分析时,忽略数量级小的各项后,可近似认为边界层垂直方向上的压力不变,且轴向力的主要形成因素是增压器两端的压力差。因此,用静压作为网格无关解,对网格无关性做出评价。在压气机的2个叶片之间取10点对压力进行监测,压力监测点分布见图3。压力验证结果见图4。图4中量纲为一数值X表示所取的10个点。

图3 压力监测点分布

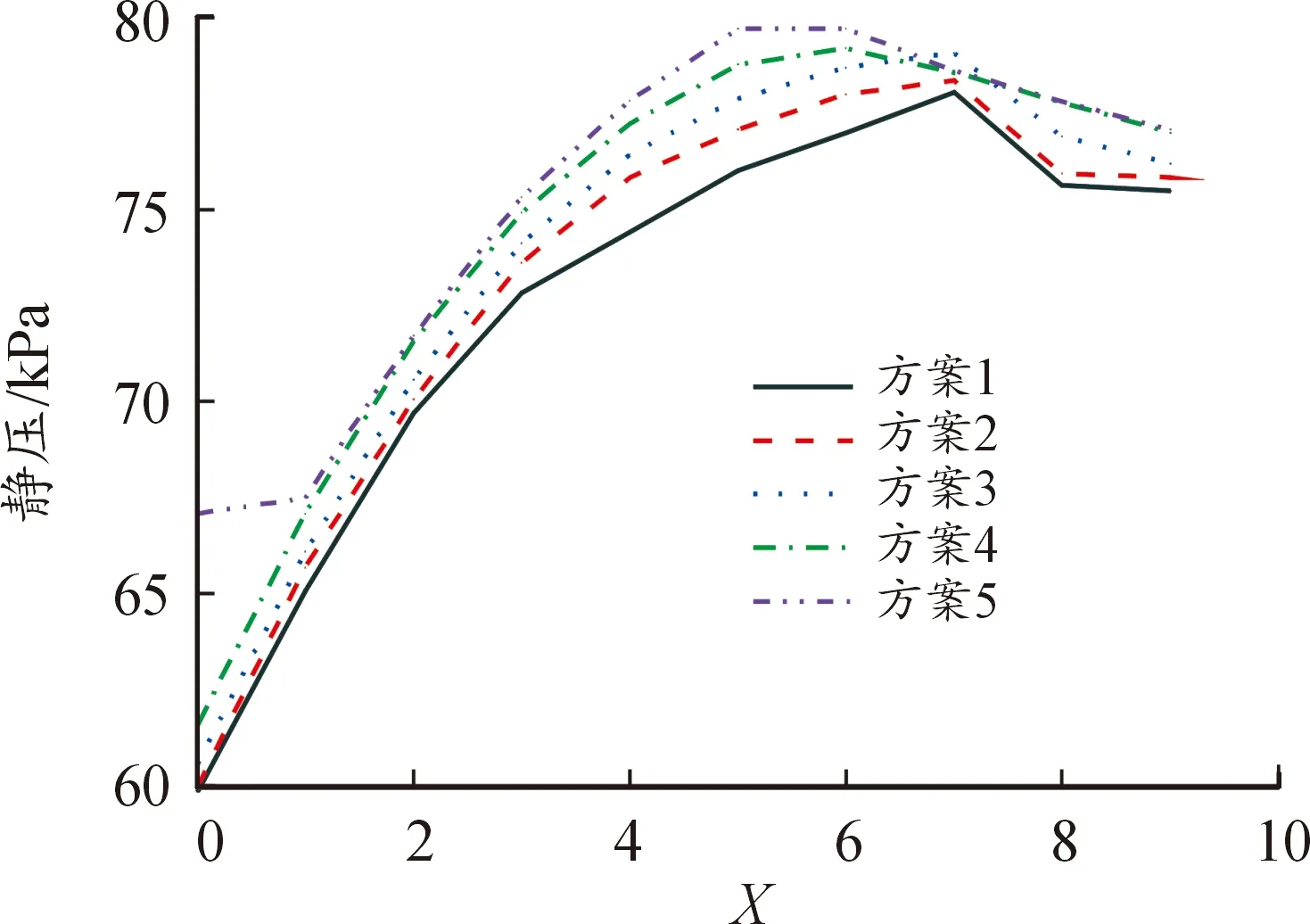
图4 压力验证结果

图4表明,监测点的压力值随着网格密度的增加而增大。方案4与5的验证结果差值不超过1.5%,为了节约计算资源,选择方案4作为计算网格。

2 边界条件设置

根据发动机在转速1 960 r/min、100%负荷下的切换过程中得到的实验数据,设置3个仿真工况来探究相继增压系统切换过程中基本增压器轴向力的变化规律。增压器转速、压气机与涡轮机压力的变化情况如表1所示。在进行瞬态轴向力计算之前,需要对其初始场进行稳态计算,稳态计算边界条件如下:增压器转速为107 000 r/min、涡轮机入口压力206 597 Pa、入口温度为584 K;压气机入口压力为101 325 Pa、入口温度为300 K;初始场轴向力分别为:涡轮机75.52 N、压气机-111.759 N。

表1 基本增压器仿真工况设置

3 仿真结果与分析

3.1 涡轮端仿真结果与分析

3.1.1切换工况1

切换工况1下,涡轮机轴向力随时间变化的曲线如图5所示。在阀门开启瞬间,约0.005 s内轴向力下降了约25 N,在0.03 s附近发生切换过程中的最大振幅30 N,是整个切换过程中振幅最大的轴向力,可能导致止推轴承受巨大的轴向力冲击。波动时间约占整个切换时间的60%。轴向力最终稳定在26.7 N左右。

图5 工况1:涡轮端总轴向力变化曲线

如图6所示,在0.03 s附近会发生幅值在35 N的振荡,随后振荡幅值逐渐降低,在0.1 s时振荡结束,涡轮机轮背轴向力稳定在310.5 N。在增压器转速下降的过程中,轮背的轴向力也呈振荡下降。

图6 工况1:涡轮端轮背轴向力变化曲线

如图7所示,涡轮叶片所受轴向力在切换开始的0.001 s内会迅速升高至-47 N,随后下降。在0.02～0.04 s期间发生幅值在10 N左右的振荡,随后振荡逐渐消失,在0.1 s后稳定在-25 N左右。在阀门打开后,涡轮叶片的轴向力迅速升高,这可能是由于转子惯性力的作用导致。阀门打开瞬间,进入涡轮端的废气量迅速减少,但由于转子轴承系统惯性力的存在,叶片转速不会突然下降,这将导致废气流在涡轮叶片的流动发展不均匀,使得流动更为复杂,所以涡轮的叶片轴向力迅速升高。另外2种切换工况下依然可以看到此现象。相反,压气机端的进气量不会迅速减少,使得压气机端的流场能延续一小段时间的顺畅。

图7 工况1:涡轮端叶片轴向力变化曲线

比较上面的涡轮端总的轴向力变化趋势和轮背的轴向力变化趋势可以发现,两者的变化趋势大致相同。为了探究引起轮背轴向力变化的因素,观测轮背压力在切换过程中的变化情况。从图8可以看出,轮背压力由涡轮入口方向处向外逐渐降低,轮背压力的数值随着时间而降低,在切换的过程中,轮背的高压区存在移动与变化,在0.031、0.036 s时涡轮轮背处会出现低压区域。

3.1.2切换工况2

切换工况2下,瞬态工况时涡轮机轴向力随时间变化的曲线如图9所示。由于转速下降的速率加快,涡端轴向力在阀门开启瞬间下降了约33 N,紧接着发生幅值为25 N的振荡;由于时间缩短,转速变化较快,使得本次工况下轴向力波动频率下降,但是波动幅值较大,在涡轮入口压力与转速变化结束之后轴向力最终稳定在36.8 N。

图9 工况2:涡轮端总轴向力变化曲线

如图10所示,轮背轴向载荷呈现随时间下降的趋势。在0.005 s时发生幅值在35N的振荡,在0.03 s时再次发生10 N的振荡,最终涡轮机轮背轴向力稳定在325.5 N。结合轮背的压力分布云图研究引起轮背轴向力变化的原因。如图11所示,轮背压力由涡轮入口方向处向外逐渐降低,在0.009 s时出现大面积的低压区,此时轴向力也处于最小值,随后高压区依然出现在入口附近,中心压力最低。

图10 工况2:涡轮端轮背轴向力变化曲线

图11 工况2:涡轮端轮背压力分布

如图12所示,涡轮叶片所受轴向力在最开始迅速升高至-50 N,随后随时间下降,最后在0.05 s时稳定在-18 N,表明工况1下叶片轴向力在阀门打开瞬间会迅速升高。

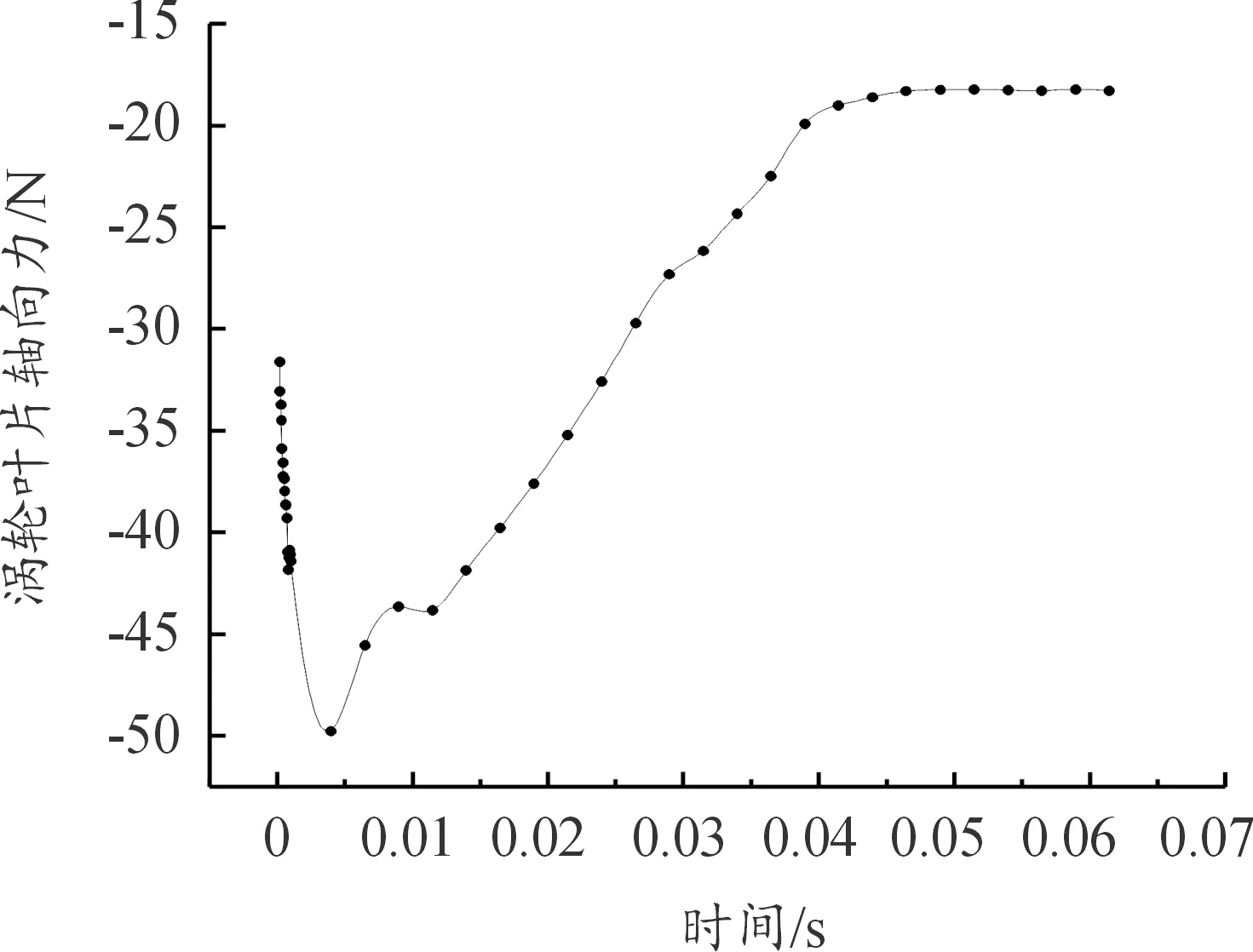
图12 工况2:涡轮端叶片轴向力变化曲线

3.1.3切换工况3

切换工况3下,涡轮机轴向力随时间变化的曲线如图13所示。轴向力随着时间下降,由75.52 N下降到18.58 N。在0.02～0.04 s时会出现幅值逐渐增大的振荡,最大可达30 N,随后逐渐下降,在0.04 s之后振荡消失。在0.1 s涡轮入口压力与转速变化结束之后,轴向力逐渐稳定在18.5 N。

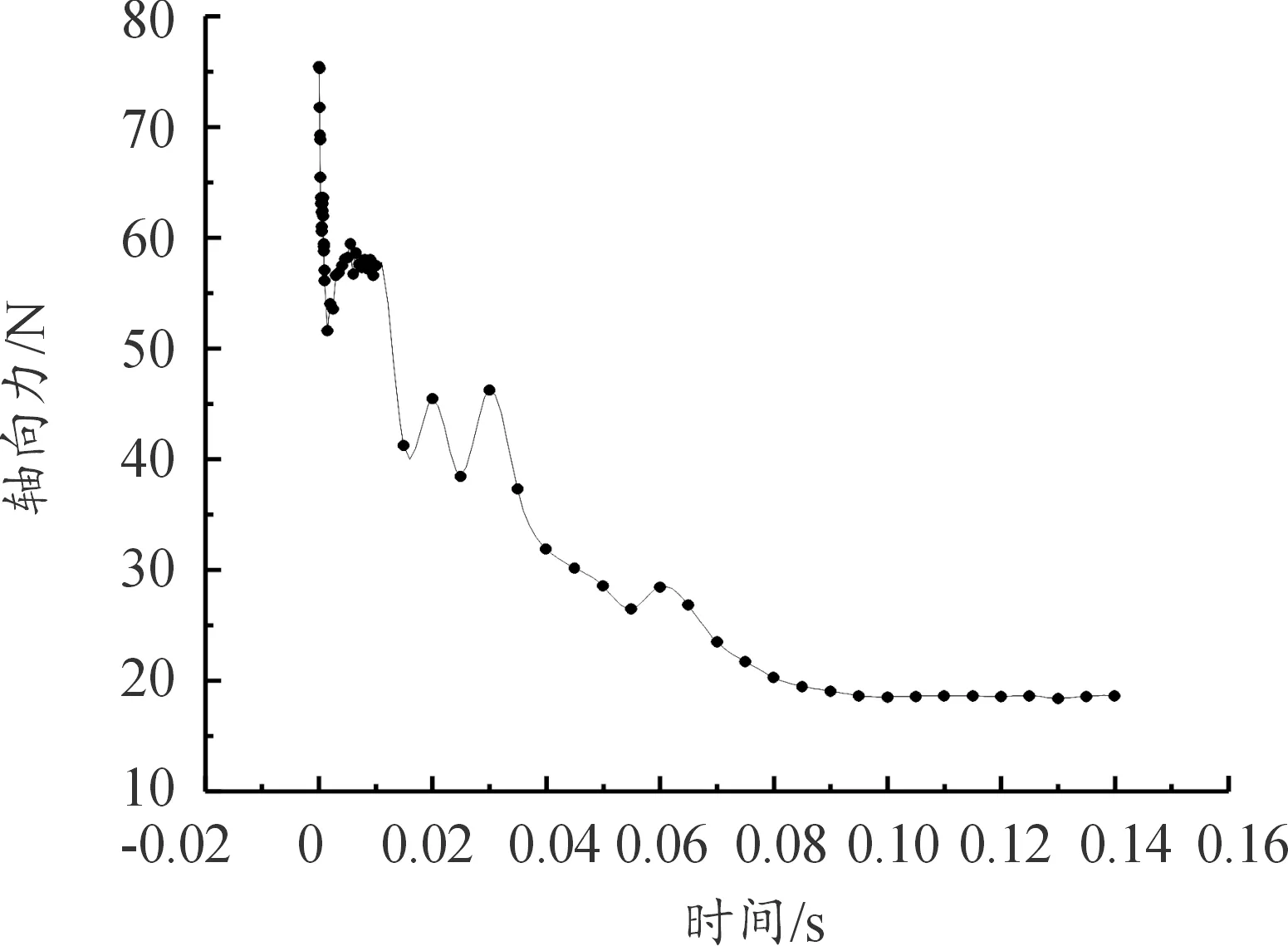
图13 工况三涡轮端轴向力变化

如图14所示,在切换过程中,轮背轴向力呈随时间下降的趋势。在0.02～0.04 s时,轮背轴向载荷出现幅值逐渐增大的振荡,最大可达40 N,随后幅值逐渐下降,在0.04 s后震荡消失,随后在0.1 s之后轮背轴向载荷逐渐稳定在297.3 N。图15为涡轮轮背处的压力分布情况,轮背压力由涡轮入口方向处向外逐渐降低,在0.03 s时在入口远端有明显的低压区。涡轮端高温高压气体由径向进入、轴向流出,表明涡轮轮背压力分布呈现出与压端不同的情况,但是涡端各个工况呈现出一定的规律性。

图14 工况3:涡轮端轮背轴向力变化曲线

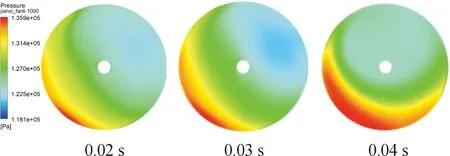
图15 工况3:涡轮端轮背压力分布

3.2 基本增压器压气机端仿真结果

3.2.1切换工况1

如图16所示,在切换过程中,压气机端轴向力在阀门开启后的0.003 s内升高了232.24 N,随后保持0.006 s后,轴向力迅速下降了211.12 N,在0.023 s后一直呈下降趋势,在0.1 s后稳定在-46.5 N。总体来看,最终轴向力减小了65.25 N,说明增压器压气机端的轴向力随着转速的下降而下降;但是从切换的角度看,压气机的轴向力在阀门打开瞬间会出现大幅的波动,且波动幅度在 230 N左右,振荡时间占总切换时间的30%。

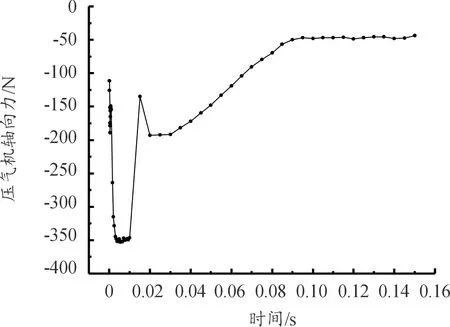
图16 工况1:压气机端轴向力变化曲线

如图17所示,切换工况1下压气机端轮背的轴向力变化趋势与压气机端总的轴向力基本相似。从切换过程看,轮背的轴向力依然经历了幅值为226 N的振荡,振荡时间占总切换时间的30%。轮背与轮毂压力分布云图如图18所示,在轮背轴向力最大时轮背的低压区明显扩大。轮背压力由内向外呈梯度增大,轮背的静压值范围较大,这是由于轮背起到承载的整体作用,而轮毂直接与气流接触,压力受流场的影响较大。可见,压气机由轴向进入,径向流出,空气在出口位置被压缩为高压气体。以下几种工况都可得到验证。

图17 工况1:压气机端轮背轴向力变化曲线

图18 工况1:压端静止件压力分布云图

如图19所示,工况1下,叶片轴向力从结果来看下降了230 N,且方向发生改变。从细节看到,叶片轴向力在阀门打开后的0.01 s过程中并没有发生大幅振荡,基本稳定。这与涡轮端叶片的轴向力形成了鲜明对比,说明压气机端由于转子惯性力作用,在涡轮端的废气流量下降之后,压气机端的进气量不会快速减少,经过大约0.01 s的延迟之后,进气量减少,轴向力发生幅值为115.3 N的振荡,在0.025 s后轴向力逐步稳定下降,0.1 s后稳定在17.5 N,轴向力指向涡轮端。

3.2.2切换工况2

如图20所示,切换结束后压气机端轴向力比开始时刻升高了15 N,由于切换时间缩短了一半,故切换过程中并没有出现小幅度的振荡,而是经过1次幅值为203 N的大幅波动,在0.05 s后轴向力保持幅值为10 N动态稳定。可见,轴向力的大幅变化主要发生在阀门开启瞬间,随后随时间逐步稳定下降。

图20 工况2:压气机端总轴向力变化曲线

从图21看出,压端轮背轴向力与压端总的轴向力变化趋势基本趋同。

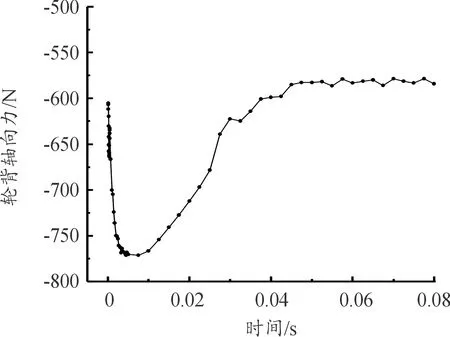
图21 工况2:压气机端轮背轴向力变化曲线

如图22所示为压端静止件压力分布云图。压力梯度由内向外逐渐升高。随着切换过程的进行,轮背低压区逐渐扩大,在0.05s时出现巨大的低压区,使得最终轴向力低于切换前。

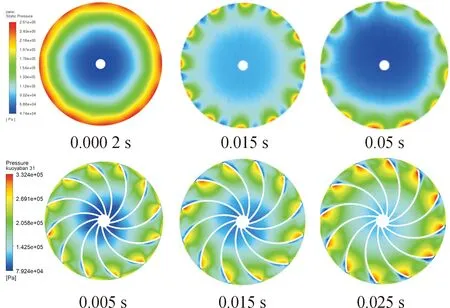
图22 工况2:压气机端静止件压力分布云图

如图23所示,在瞬态过程中叶片的轴向力随时间呈下降趋势,与初始值相比下降了133.18 N。在阀门打开后的0.005 s内,叶片轴向力基本稳定在-180 N,随后以很快的速度下降到31 N。这可能是由于切换时间缩短,叶片轴向力的下降速度相比于工况1更加迅速导致。

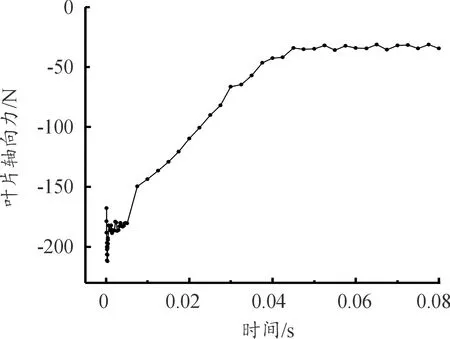
图23 工况2:压气机端叶片轴向力变化曲线

3.2.3切换工况3

如图24所示,阀门打开后的0.016 s内发生了幅值高达238 N的波动,随后轴向力一直呈线性下降趋势,直到0.1 s后稳定在-47.68 N。压气机端总的轴向力下降了65.1 N。

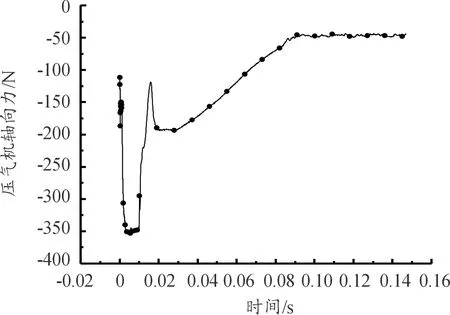
图24 工况3:压气机端总轴向力变化曲线

如图25所示,切换过程中压气机端轮背的轴向力变化趋势与压气机总轴向力的变化趋势基本相似。轮背的轴向力相较于初始值-605.883 N下降了106.51 N。轮背的轴向力在阀门打开后的0.016 s内发生了幅值为227.7 N的振荡。从图26中看出,这可能是由于轮背的压力分布发生变化,出现较大面积的低压区所导致。

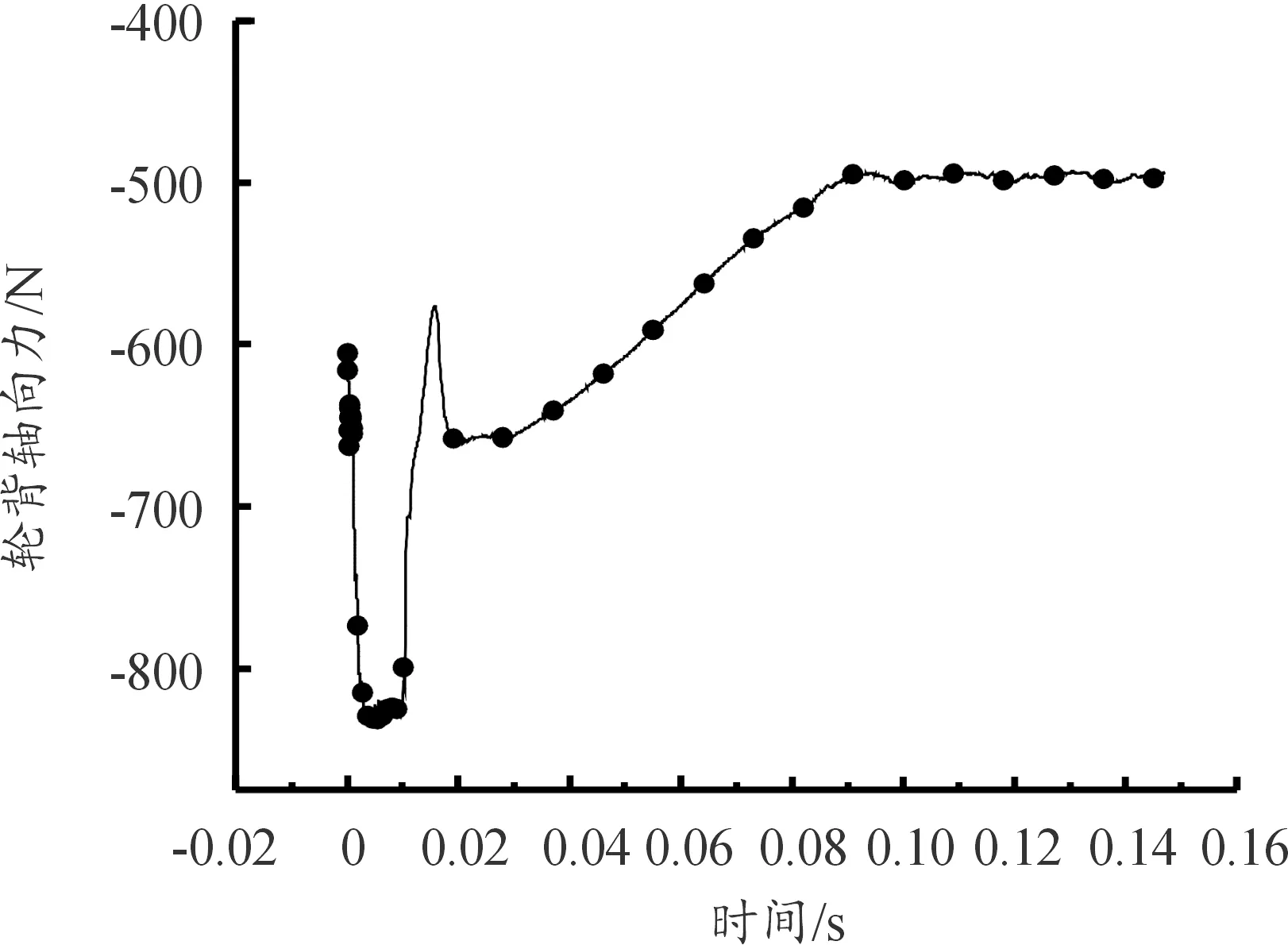
图25 工况3:压气机端轮背轴向力变化曲线

图26 工况3:压气机端静止件静压分布云图

3种切换工况下涡轮增压器的整体的轴向力变化情况如图27所示。

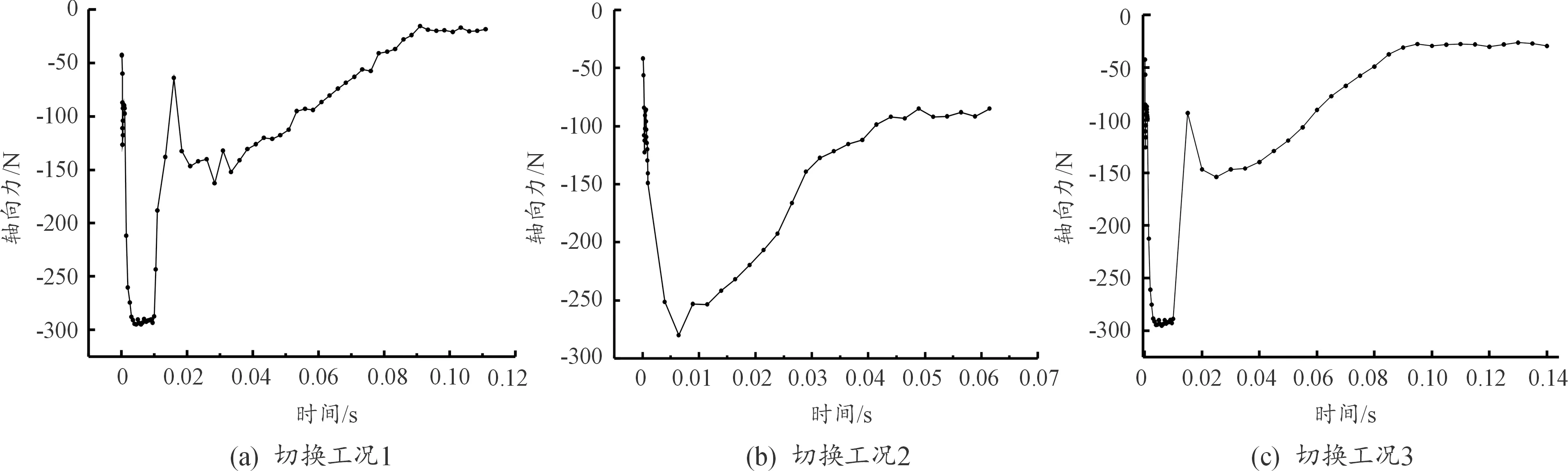
图27 基本增压器轴向力随时间变化曲线

4 结论

1) 对比瞬态工况1与2,切换时间越长,阀门开启初期轴向力波动越大,波动持续时间约占切换时间的40%;最终稳定时的轴向力越低。但由于工况2的切换时间缩短一半,故轴向力经过一次大幅波动之后便呈线性下降趋势。

2) 对比瞬态工况1与3,相同时间内转速下降的幅度越大,瞬态切换中轴向力振幅越大,越难以呈线性稳定下降。

3) 从总体轴向力变化趋势来看,压气机端轴向力变化主导了增压器总的轴向力变化。压端轴向力的变化受到压气机端轮背轴向力的主导,而轮背轴向力是由于轮背气体静压的存在而形成,其本质是气体泄漏进入轮背间隙而形成上述结果。因此,压气机与涡轮机端的轮背气体泄漏量是影响增压器轴向力的主要因素。涡端在切换瞬间叶片的轴向力变化最剧烈。