冲击载荷下砂岩动态拉伸力学及能量耗散特征

李金洋

(国家能源集团陕西神延煤炭有限责任公司西湾露天煤矿, 陕西 榆林 719054)

1 前言

近年来,随着浅部煤炭资源枯竭[1],煤炭资源开采向中西部转移已成为必然趋势,其中蒙陕地区已成为我国煤炭资源主要供给地。受爆破掘进、机械割煤等矿山开采活动的动力扰动影响,导致蒙陕矿区动力灾害形势日益严峻。鉴于岩石抗拉强度远远低于抗压强度,实际开采活动中岩体结构通常为张拉破坏形式,因此开展冲击载荷下砂岩动态拉伸力学响应行为的研究具有十分重要的意义。

目前国内外学者针对煤岩动态抗拉性能已取得一系列成果,获得了不同类型煤岩动态抗拉强度、能量耗散特征、破坏特征等,但集中于巴西圆盘实验间接拉伸测试煤岩抗拉性能。其中曹丽丽等[2]探究了煤系砂岩动态拉伸破坏的3个阶段。周磊等[3]对比分析了3种典型砂岩材料的抗拉强度差异。夏开文等[4]开展不同加载条件下的巴西劈裂实验,定量表征了岩石拉伸过程中的过载现象。刘运思等[5]探究了层理角度及加载率对板岩巴西劈裂破坏模式的影响。杨仁树等[6]借助超高速摄像系统,对比分析了波阻抗对岩石应变场演化规律的影响,并指出红砂岩、灰砂岩和花岗岩的加载率敏感性差异。宫凤强等[7]提出巴西圆盘试验中岩石拉伸弹性模量的解析算法。吴秋红等[8]借助改进的霍普金森压杆系统,对不同热冷处理后的花岗岩试样开展冲击劈裂实验,获得不同温度、加载率对岩石动力学响应的影响。赵毅鑫等[9]探讨了冲击速度及层理倾角对煤样动态抗拉强度的影响,认为煤岩抗拉强度随冲击速度的增大而增大。刘德俊等[10]开展了不同循环冻融次数下砂岩巴西劈裂实验,并借助电镜扫描及高速摄像探究冻融循环次数对砂岩微观破坏特征的影响。韩秀会等[11]基于变形场时空演化规律,获得煤样巴西劈裂破坏模式及变形时空演化特征。王月华等[12]研究了热处理对花岗闪长岩静动态抗拉强度的影响,并对比分析了动静加载的影响差异及微观改变。王浩等[13]获得了冲击载荷下饱水凝灰岩的动态断裂韧性及分形维数演化规律。杨科等[14]探究了煤样动态劈裂破坏过程中含水率对能量耗散的影响,认为耗散能密度随冲击载荷的增大呈线性增长关系。郭占峰等[15]提出了动态拉伸敏感性指标,可准确表征岩石等脆性材料的拉伸率效应。赵建平等[16]研究了含水率于砂岩动抗拉强度的关系,指出岩石的动拉伸强度随加载率的增加而增加,且率相关性与含水率显著关联。马泗洲等[17]借助数值模拟,获得波阻抗对复合煤岩体动力学响应特征的影响。

前人研究成果虽然对砂岩巴西劈裂开展了大量实验,但仍缺乏不同加载率下砂岩动力学响应的系统研究。为探究加载率影响下砂岩动态拉伸力学特性,借助SHPB装置对砂岩开展劈裂实验,分析不同加载率下砂岩动态拉伸强度、峰值应变、能量耗散特征等,以期为煤矿围岩控制提供理论参考。

2 SHPB实验系统及原理

2.1 试样制备

实验砂岩取自陕西榆林某煤矿,选自大块完整岩块,且无明显节理、裂隙等缺陷。根据岩石力学与工程学会规定[18],完整、均质性较好的砂岩,经取芯、切割、打磨后的标准试样(直径×高:50 mm×25 mm),需满足端面不平行度低于0.02 mm、不垂直度低于0.05 mm。同时,为保证试样均质性良好,避免岩体赋存结构差异的影响,借助非金属超声波探测仪获得试样纵波波速,剔除纵波波速超过10%的试样。标准巴西圆盘试样,具体如图1所示。试样基本物理力学参数见表1。

表1 砂岩基础物理力学参数

图1 部分标准砂岩试样

2.2 实验系统

冲击加载实验借助φ50 mm的分离式霍普金森压杆系统,SHPB系统装置如图2所示。SHPB装置包括冲击加载系统(空气压缩机、)、杆件系统(入射杆:3 000 mm、透射杆2 500 mm、圆柱型撞击杆:400 mm、吸能杆:1 000 mm)、缓冲系统(阻尼器、固定架等)、信号采集机处理系统(桥盒、普通应变片、超动态应变仪、示波器等)。在巴西劈裂实验中,试样放置于入射杆与透射杆中心位置,当撞击杆在压缩空气作用下,以固定速度碰撞入射杆,在入射杆端面产生入射波,当入射波传递至试样与杆件接触端面时多次反射透射,最终导致试样变形破坏。其中被反射的脉冲通过入射杆的应变片测试,透射的脉冲信号则被透射杆的应变片测试获得。

图2 SHPB实验系统示意

2.3 实验原理

冲击载荷下试样中心拉伸应力与静载巴西劈裂实验计算公式见式(1)。

(1)

式中,P1、P2分别为砂岩试样两端端部载荷;D为试样直径,取50 mm;B为试样厚度,取25 mm。

基于弹性压杆理论,获得端部载荷P1、P2计算公式。

(2)

式中,A为压杆端面面积;Eb为杆件弹性模量,取206 GPa;εI、εR、εT分别为试样入射、反射、透射应变。

当试样冲击加载过程,满足应力均匀假设时,两端应变相等,即存在

εI+εR=εT

(3)

联立式(1)、(2)、(3),可得式(4)。

(4)

实验设计冲击速度分别为4 m/s、6 m/s、8 m/s、10 m/s,开展不同冲击速度下的砂岩动态巴西圆盘实验,探究砂岩动态拉伸力学响应行为。同时,为保证实验数据可靠性,需对实验结果开展应力平衡检验,即冲击载荷下试样两端需达到应力平衡状态[19],典型试样的应力平衡状态如图3所示。其中,入射波、反射波的叠加波与透射波基本重合一致,表明试样基本达到应力平衡状态。

图3 应力平衡特征

2.4 加载率计算

动态巴西劈裂实验中通常采用加载率为实验变量,探究煤岩的动态劈裂力学特性。图4所示为动态巴西劈裂实验中典型砂岩应力时程曲线。基于一维应力波理论,定义曲线上升阶段直线区域的斜率为动态巴西劈裂实验中试样加载率[20]。如图4所示,加载率为时间0.04 ms至0.06 ms时间内的直线斜率,即加载率值为402 GPa/s。

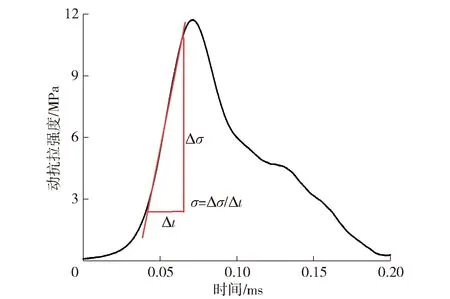
图4 应力时程曲线

3 动态力学特征

3.1 应力应变曲线特征

砂岩应力应变曲线可表征巴西劈裂实验中试样动态力学响应行为,可表征试样动态拉伸力学特性。其中,不同加载率下砂岩的应力应变曲线如图5所示。

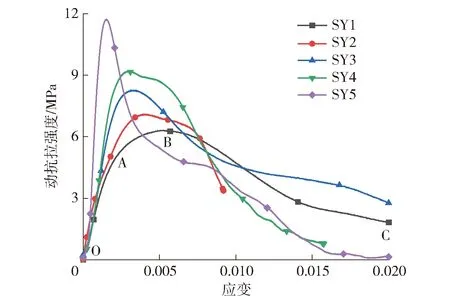
图5 应力应变曲线特征

由图5可知,不同加载率下试样动态应力应变曲线基本一致,具备显著的非线性特征,包括弹性OA、塑性屈服AB、破坏阶段BC。对比冲击压缩下煤岩类材料的应力应变曲线可知,砂岩应力应变曲线的初始阶段不存在明显的压密阶段。原因在于,砂岩质地相对均匀,内部无显著的裂隙孔隙结构,导致冲击载荷作用初期基本无裂隙闭合现象。以试样SY1为例,随着加载持续进行,砂岩进入弹性阶段,该阶段砂岩未产生明显的裂隙等微缺陷,且应力随应变的增大而线性增加,同时加载率越大,应力应变曲线的弹性阶段斜率越大。随着应变的增加,砂岩试样应变持续增加,变形曲线过渡至屈服阶段,此时试样内部裂纹萌生发育,曲线的非线性显著增加。当应力达到极限抗拉强度时,试样发生显著变形及破坏,导致试样抵抗拉伸破坏的能力显著降低。

3.2 动抗拉强度特征

岩石动抗拉强度可表征冲击载荷下岩石抵抗变形破坏的能力。为探究巴西劈裂过程中砂岩动抗拉强度与加载率的关系,绘制不同加载率下砂岩动抗拉强度变化曲线,具体如图6所示。

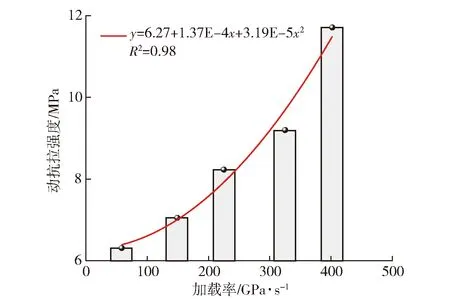
图6 动态拉伸强度演化特征

由图6可知,冲击载荷下砂岩动态拉伸强度随加载率的增大而增大,呈显著的二次函数关系,关联系数R2=0.98。其中,当加载率为58.3 GPa/s时,试样动抗拉强度最低,最小值为6.31 MPa;当加载率增大至149 GPa/s、225 GPa/s、325 GPa/s、402 GPa/s时,砂岩动抗拉强度分别为7.05 MPa、8.23 MPa、9.20 MPa、11.71 MPa,较初始加载率依次增加了11.73%、30.43%、45.80%、85.58%,其中最大值与最小值相差5.40 MPa。原因可能在于,随着冲击载荷的增大,砂岩抵抗拉伸变形能力显著增加;此外,随着加载率的增大,试样变形破坏相对滞后,导致砂岩抗拉强度显著增加。

3.3 峰值应变特征

岩石峰值应变可反映冲击载荷下岩石起裂时刻的破坏程度。为探究巴西劈裂过程中砂岩峰值应变与加载率的关系,绘制不同加载率下砂岩峰值应变变化曲线,具体如图7所示。

图7 砂岩峰值应变演化特征

由图7可知,冲击载荷下砂岩峰值应变随加载率的增大而减小,呈显著的负相关关系,关联系数R2=0.93。其中,当加载率为58.3 GPa/s时,试样峰值应变最高,最大值为0.005 1;当加载率增大至149 GPa/s、225 GPa/s、325 GPa/s、402 GPa/s时,砂岩动抗拉强度分别为0.004 2、0.003 1、0.002 9、0.001 5,较初始加载率依次降低了17.65%、39.22%、43.14%、70.20%,其中最大值与最小值相差0.003 6。原因可能在于,随着冲击载荷的增大,砂岩仅需发生很微弱的变形便达到强度极限值,一定程度上反映了弹性模量的增加,即抵抗变形能力的增强。

4 能量耗散特征

基于一维弹性波理论及均匀性假设可知,由于岩石内部存在节理、裂隙、孔隙等微缺陷,冲击载荷下应力波携带的能量部分在试样端面被反射、透射,另一部分被试样吸收,主要用于岩石内部原生裂隙、节理等缺陷的扩展及新生裂隙的萌生与发育,极少部分以声、光、热、动能、辐射等形式耗散。其中95%的能量用于岩石内部裂隙的萌生、发育、扩展等,5%的能量以各类形式耗散[21]。借助入射波、反射波、透射波的应变信号,获得相应砂岩试样的入射能WI、透射能WT和反射能WR,具体计算公式为[22]

(5)

根据能量守恒定律,忽略破碎动能及其他形式的耗能,即破碎耗能Wd近似等于吸收能WS,可以得到试样吸收能WS。

WS=WI-WR-WT

(7)

为表征试样能量耗散演化特征,引入能量耗散率,即耗散能与入射能的比例w见式(8)。

(8)

式中,V为试样体积。

4.1 能量时程曲线特征

不同加载率下砂岩能量时程曲线演化规律基本一致,为探究冲击载荷下砂岩拉伸破坏过程的能量演化规律,选取典型砂岩能量耗散曲线,具体如图8所示。

图8 能量时程曲线特征

由图8可知,随着冲击载荷作用时间的增加,入射能、反射能、透射能均显著增加,后趋于一稳定值。结合应变应变曲线特征,可将能量时程曲线划分为3个阶段。

(1)弹性储能阶段(AB阶段0～0.10 ms):冲击载荷作用下试样处于弹性变形阶段,该阶段试样吸收的能量速率相对缓慢,即曲线斜率较低,此时试样将吸收的能量以弹性变形能的形式储存于试样内部。

(2)塑性变形储能阶段(BC阶段0.10～0.25 ms):该阶段试样处于塑性屈服阶段,不同能量时程曲线斜率接近线性增长。原因在于砂岩与杆件存在波阻抗失衡,导致应力波在入射杆、透射杆、试样内多次传递,导致试样入射能、反射能、透射能等获得补充,进而诱发试样内部裂纹萌生、扩展,吸收大量能量,过渡至塑性变形阶段。

(3)破坏稳定阶段(CD阶段0.25～0.3 ms):该阶段试样显著变形破坏,且不同能量的曲线斜率均接近0。原因在于,该阶段试样内部裂纹充分发育,原有弹性能获得释放,导致能量趋于稳定。

4.2 入射、反射、透射能的变化特征

巴西劈裂过程中砂岩入射能、反射能、透射能与加载率密切关联,二者演化规律曲线如图9所示。

图9 能量演化特性

由图9可知,不同加载率下各能量拟合曲线均呈正比例增长,可采用一次函数y=ax+b拟合,拟合系数:R2≥0.84。同时,对比分析可知,入射能随加载率的增长速率最快,透射能增长相对缓慢(斜率:入射能>反射能>透射能)。原因可能在于,入射能是冲击加载实验中外界能量的来源,其数值大小由撞击杆的冲击速度决定,而加载率与冲击速度存在显著关联,故入射能随加载率增长相对显著。而反射能与砂岩内部微观缺陷分布特征存在密切关联,因此受砂岩内部原生结构的影响,其增长趋势弱于入射能。其中透射能变化趋势与透射能在全部能量的比例存在一定联系,与砂岩波阻抗大小存在显著关联。

4.3 能量耗散演化特征

能耗率反映劈裂过程中砂岩内部裂隙萌生、发育,导致试样丧失抵抗拉伸破坏全过程中能量演化规律。借助能耗率,可有效表征砂岩拉伸破坏的本质。其中,能耗率与加载率关系如图10所示。

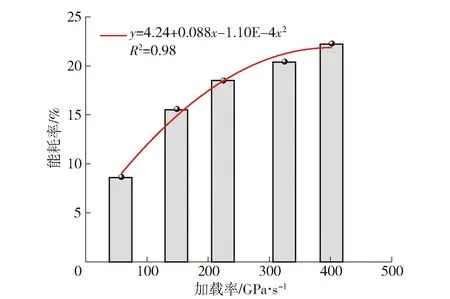
图10 砂岩能耗率演化特征

由图10可知,冲击载荷下砂岩能耗率随加载率的增大而增大,呈显著的二次函数关系,关联系数R2=0.98。其中,当加载率为58.3 GPa/s,试样能耗率最低,最小值为8.66%;当加载率增至149 GPa/s、225 GPa/s、325 GPa/s、402 GPa/s时,砂岩动抗拉强度分别为15.59%、18.50%、20.43%、22.28%,较初始加载率依次增加6.93%、9.84%、11.77%、13.62%。原因可能在于,随着加载率的增大,试样从完整状态过渡至破碎/粉碎状态,该过程中耗散能用于砂岩裂纹扩展与发育,具备显著的率相关性。此外随着加载率的增大,试样耗散过程中的能量分配显著改变,即用于砂岩破碎的能量占比增加。

5 结论

针对砂岩动态拉伸力学响应行为,开展不同加载率下砂岩力学、能量耗散特性研究,结论如下:

(1)砂岩应力应变曲线呈非线性阶段特征,包括弹性阶段、塑性屈服阶段、破坏阶段;砂岩的动抗拉强度随加载率的增大而增大,呈二次函数关系;砂岩峰值应变随加载率的增大而减小,呈一次负相关关系。

(2)冲击载荷下砂岩拉伸耗散过程包括:弹性储能阶段(0～0.10 ms)、塑性变形储能阶段(0.10～0.25 ms)、破坏稳定阶段(0.25～0.3 ms)。

(3)巴西劈裂过程中砂岩的入射能、反射能、透射能随加载率的增大而增大,呈一次函数关系;能耗率与加载率呈二次函数关系(R2=0.98)。