超振荡望远成像系统中球差影响分析

柳少扬，杜文娟*，焦 蛟，姚 纳，孙 旭，倪 磊，李文凯

1 湘潭大学物理与光电工程学院，湖南 湘潭 411105；

2 电子科技大学航空航天学院，四川 成都 610054；

3 西南科技大学制造科学与工程学院，四川 绵阳 621010；

4 中国科学院光电技术研究所光电工程总装中心，四川 成都 610209

1 引言

由于光的衍射，望远系统的最小角分辨力是1.22λ/D[1]，被称为瑞利判据。为了获得小于瑞利判据的分辨力，科研人员提出了许多超分辨成像技术。荧光显微成像技术广泛应用于远场超分辨成像，例如，全内反射荧光显微技术 (total internal reflection fluorescent microscopy，TIRFM)[2]，受激辐射损耗显微技术 (stimulated emission depletion microscopy，SEDM)[3]等。但是，当目标物位于远处时，无法使用荧光染剂标记被测物。近几年，频谱平移技术的兴起，实现了无荧光标记的远场超分辨成像，例如，傅里叶叠层显微成像 (fourier ptychography microscopy，FPM)[4]。该技术使用不同角度光线照明目标物，平移了目标物的频谱，将截止频率以外的空间频率搬移到了成像系统的通带内，保留了目标物的高频信息从而提升分辨力。但是，很难对远处的目标物照明。因此，上面这些应用于显微系统的超分辨成像技术很难移植到望远系统中。

近年来，超分辨成像领域发展出一种新的技术，即对光场进行超振荡调制[5-6]，该技术不需要特殊照明光场，可应用于望远系统。2006 年Berry 在数学上证明了超振荡现象，即局部视场内光场振荡速度超过其最快的傅里叶分量[7]，空间域上压缩了焦斑，理论上能实现任意小的光能量聚焦。1952 年Torraldo 将超分辨技术引入光学领域，发展成了光瞳滤波技术[8-10]，该技术可以超振荡调制光场，实现超瑞利判据聚焦[11]。2008 年Huang 设计了由金属屏上的纳米孔阵列模拟的超振荡透镜(super-oscillatory lens，SOL)[12]，实验中实现了660 nm 波长的平面波聚焦，焦斑约为0.6倍瑞利判据。2017 年Muyuan Li 结合矢量角谱和遗传算法的优化方法设计得到SOL，在光轴上实现任意数量尺寸小于瑞利判据的焦斑，且能量分布符合理论设计[13]。另外，光瞳滤波技术还可实现超分辨成像[14-15]。2015 年罗先刚团队提出超振荡望远系统，使用532 nm 激光照明双圆孔，在实验中得到的最小分辨力为0.55 倍瑞利判据，并且叠加多个局部视场，实现了对复杂目标和大型目标的成像[16]。2020 年Wenli Li 基于多相位调制(multiple-phase-modulated，MPM)方法，提出具有高聚焦效率的SOL，降低旁瓣的同时其工作距离达到了2 mm[17]，远高于先前报道的微米级SOL 工作距离。

光场的超振荡调制还可通过超表面得以实现，不仅能够超分辨聚焦及成像，同时在一定波长范围内具有消色差[18]、增大入射角[19]等功能。2018 年Santiago Legaria 设计得到一种基于六边形单元结构的超表面SOL，并提出一种基于进化算法的优化方法，以减小旁瓣，提高聚焦处的强度[20]。同年罗先刚团队利用超表面相位调制的近似无色散优点，提出一种用于宽带超分辨成像的超表面超振荡滤波器，实验实现了其在可见光波段的分辨力约为瑞利判据的0.64 倍[21]，该团队最近也提出了角向超振荡透镜[22]等新方法。然而，值得注意的是，利用超表面结构实现超振荡调制的原理相对复杂，其加工也具有一定难度。2022 年有研究报道了利用平面液晶几何相位器件构建的超振荡器件[23]实现超分辨，但SOL 具有成本优势。

在光学系统中，球差会降低其分辨力，且无法完全消除。目前已有研究工作报道了球差对共聚焦显微(confocal microscopy，CM)[24-25]、宽视场显微(widefield microscope，WFM)[26-27]以及共聚焦光片显微(confocal light sheet microscopy，CLSM)[28]等系统的影响。对于望远系统，研究人员提出了校正其球差的方法。2009 年Jong Ung Lee 在设计三镜望远系统的过程中，利用圆锥常数和两个自由度对球差等四种三阶像差进行了校正[29]。2019 年González-Acuña 基于几何光学原理，提出了反射-折射望远系统非球面镜设计的解析通解，能推导出透镜表面的形状，用于校正由系统中任意数量的前折光面产生的球差[30]。关于球差对SOL，特别是在望远成像方面的影响，目前相关研究工作报道较少。除此之外，针对超振荡望远系统，由于加工误差，制备结构精度较难达到校正球差的理论值，因此，分析超振荡望远系统中球差带来的影响，以及确定该系统下相应的球差容许范围，至关重要。

本文研究了超振荡望远系统中球差对成像的影响，并计算出该系统下初级球差的容许范围。在1.5 倍瑞利判据的视场内，球差会导致强度点扩散函数的旁瓣升高，降低系统的分辨力。基于光学超振荡原理，利用线性规划的优化方法设计望远系统，在532 nm 工作波长下最高能分辨中心距为0.68 倍瑞利判据的三缝。建立了超振荡望远系统球差的定量分析数学模型，对于该系统，最大容许均方根(root mean square，RMS)值为0.041 倍波长的初级球差干扰。同时，研究了窄带情况下球差对该系统成像的影响。本文在光学测量、环境监视、超分辨望远等领域具有潜在的应用。

2 球差对超振荡望远系统点扩散函数的影响分析

超振荡函数由多个波函数叠加而成，在局部区域，其频率超过了波函数的最高频率。本文设计了一个超振荡望远成像系统，并使用三缝作为目标物，来测试分辨能力。图1 是超振荡望远成像系统的示意图，白光光源经过窄带滤波片后得到中心波长为532 nm 的非相干光。相比于相干光照明，非相干光的光场没有同频率、同振动方向、恒定相位差[31]等严苛条件。非相干光不容易被大气湍流等干扰影响，适合望远系统，另外非相干光照明能得到分辨力更高的成像结果[32]。L1和L2是透镜，目标物在L1的前焦面处，经过非相干光照明后，相当于无穷远处的物体。经过超振荡器件(super-oscillatory，SO)及L2的聚焦后，在CCD 相机上形成像。

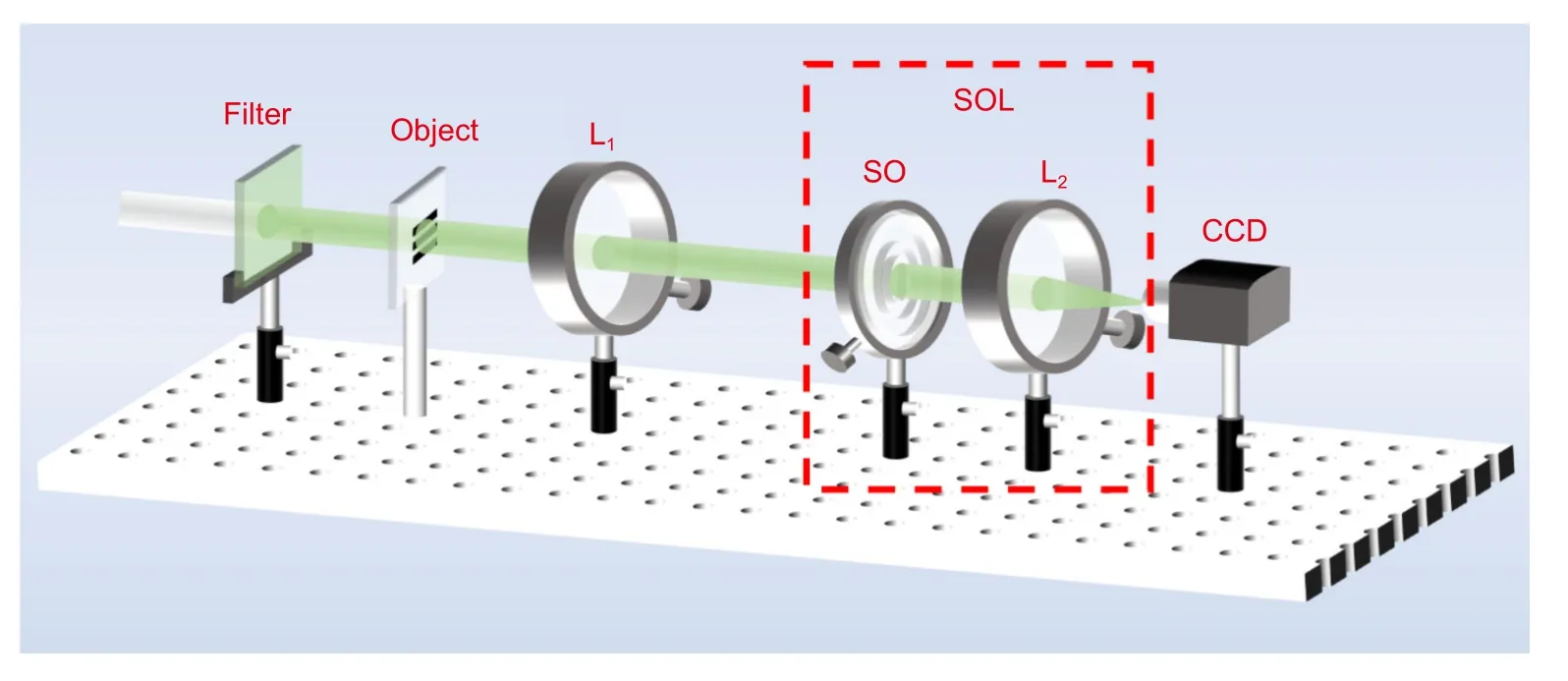
图1 超振荡望远成像系统示意图Fig.1 Schematic of the super-oscillatory telescopic imaging system

超振荡望远系统的核心是SOL，本文基于Torraldo 方法[9,33-34]设计SOL，该方法将SOL 的设计问题转化为优化问题，随后将优化问题变为线性规划问题[35-36]，通过求解线性规划的全局最优解优化得到SOL 的参数。物空间的点光源经望远系统后，其能量主要分布在焦平面附近，可以使用焦平面的光强分布(强度点扩散函数)来研究成像结果。图2(a)是SOL 压缩系统强度点扩散函数示意图，图2(b)是SO的径向截面图，垂直入射的平面波经过SO 和透镜后，若满足菲涅耳近似条件，那么焦面上强度分布由式(1)给出：

图2 (a) SOL 压缩强度点扩散函数示意图；(b) SO 的径向截面图Fig.2 (a) Schematic of the SOL compresses the intensity point spread function (PSF);(b) Section of the SO along the diameter direction

其中：u(r1)是平面波经过SO 后的复振幅，J0是零阶Bessel 函数，r1、r2分别表示出瞳面极坐标和焦面极坐标。工作波长λ为532 nm，透镜焦距f为1000 mm，透镜半径R为4 mm。

SOL 的工作原理是其中的SO 调制波前相位，使得焦斑的主瓣变窄，为获得尺寸小于瑞利判据的焦斑，需设计相应的SO。预先设置强度点扩散函数I(r2)，第一零点位于0.65r0(r0=0.61λ/NA，表示1 倍瑞利判据)处，视场为3r0，视场内最高旁瓣与主瓣高度之比-旁瓣比(sideloberatio，SR)为0.05。确定以上的约束条件后，将焦面中心强度I(0)作为优化目标，当其达到最大值时可得到相应的u(r1)。优化后径向强度点扩散函数如图3(a)所示，可以看出该点扩散函数符合预先设置。其对应u(r1)的相位Ф(r1)如图3(b)所示，即SO 的相位调制函数，图中可知获得的π 相位突变点分别为 0.202R(0.808 mm)、0.404R(1.616 mm)、0.595R(2.38 mm)、0.776R(3.104 mm)、0.927R(3.708 mm)。可知，SO 是0，π 相移的纯相位器件。

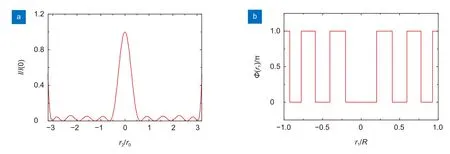
图3 (a) 优化后径向强度点扩散函数；(b) SO 的相位调制函数Fig.3 (a) The intensity PSF along the diameter direction after optimization;(b) Phase modulation function of the SO

在几何光学中，平行光经过透镜后，理论上应该汇聚于一点。但是，由于透镜的中心区域和边缘区域对光的聚焦能力不同，导致平行光在焦面上并不是形成一个点，而是一个以光轴为对称中心的弥散圆，这种像差被称为球差。对于SOL，其球差对成像效果的影响亦不可忽略。1934 年荷兰科学家Zernike 提出了Zernike 多项式[37]用于描述像差，如式(2)：

式中：

式(2)中r和θ表示相位面上的归一化极坐标，cnm、snm是像差系数，m、n取不同值代表不同的像差，δm0是克罗内克符号，是n次多项式。初级球差的大小和曲率半径、厚度、折射率密切相关，而高级球差的数值较小且相对固定，校正球差的过程就是改变初级球差，最理想为初级球差和高级球差互相补偿[31]，但由于加工等误差无法实现也无必要，只需将初级球差限制在一定范围内即可。当n=4，m=0 时，Zernike 多项式代表初级球差。对于初级球差，由于m为0，此时Zernike 多项式Wnm(r,θ)与角度坐标θ无关，初级球差带来的相位变化是。对于高阶球差，m取值均为0，因此也适用这一结论。本文以初级球差为例，考虑球差对系统的影响，则球差影响下超振荡望远系统强度点扩散函数为

超振荡望远系统径向强度点扩散函数如图4(a)所示，其中红线为无球差情况下强度点扩散函数，其第一零点位于0.65r0，半峰全宽(full width at half maxima，FWHM)是0.5776r0。蓝线为考虑RMS 值为0.042λ的初级球差情况下强度点扩散函数，其第一零点位于0.59r0，FWHM 是0.5494r0，中心高度是前者的1.921 倍。图中可知，球差带来视场中的高旁瓣，SR 是1.72，超过了线性优化中的约束条件，影响超振荡望远系统成像质量。图4(b)为RMS 值为0.042λ的初级球差分布图。

图4 (a) 超振荡望远系统径向强度点扩散函数；(b) RMS 值为0.042λ 的初级球差分布Fig.4 (a) The intensity PSF along the diameter direction in the super-oscillatory telescopic system;(b) Distribution of the primary spherical aberration with a RMS value of 0.042λ

考虑到图1 中窄带滤波片无法滤出单一工作波长，仍旧存在一定带宽，因此需要分析在窄带范围内超振荡望远系统中球差带来的影响。窄带情况下透镜焦距变化可忽略不记。图2 中SO 结构若采用石英玻璃基底制备，需要满足在532 nm 工作波长下玻璃台阶能够产生π 的相位差。该相位差可由光经过覆盖台阶的区域相比于没有覆盖台阶的区域所产生d(n-1)的光程差决定，其中d为玻璃台阶的高度，n为玻璃的折射率，因此相位差Ф由式(6)确定：

岸线类型识别主要采用图上人工交互法的方式识别和外业核查属性相结合的方式进行岸线类型。结合海岸线数据等已有岸线调查矢量信息，遵循岸线识别原则，利用不同类型岸线在影像上的形态特征、纹理特征等特征，识别人工岸线和自然岸线类型。

532 nm 工作波长下相位差Ф=π 时，计算得出玻璃台阶的高度d=578 nm。窄带范围内，当工作波长变化时，该结构带来的相位差Ф将不再是π。本文以中心频率为532 nm 工作波长、10 nm 带宽的滤波片为例，讨论窄带情况下不同初级球差对系统强度点扩散函数中心值、FWHM 的影响，如图5 所示。图5(a)是527 nm、532 nm、537 nm 工作波长下不同初级球差系统强度点扩散函数的中心值相对于532 nm 工作波长无球差系统强度点扩散函数中心值的变化。由图可知，在上文给定的SO 结构下，不同工作波长下中心强度及FWHM 随初级球差RMS 值的变化规律是不同的。其中，527 nm、532 nm 工作波长的中心强度随RMS 值增加而增加，而537 nm 工作波长的中心强度随RMS 值在0.032λ处达到最小值。在相同的RMS 值条件下，527 nm 工作波长的中心强度最大。图5(b)是527 nm、532 nm、537 nm 工作波长下不同初级球差系统强度点扩散函数的FWHM变化。其中527 nm、532 nm 工作波长下，RMS 值低于0.045λ的初级球差对FWHM 影响较小，而537 nm 工作波长下FWHM 在0.042λ处达到最小值。在相同的RMS 值条件下，527 nm 工作波长的FWHM最大。

图5 (a) 不同工作波长，不同初级球差系统强度点扩散函数相对中心值；(b) 不同工作波长，不同初级球差系统FWHM 相对值Fig.5 (a) Relative central values of the intensity PSF in different primary spherical aberration systems under different working wavelengths;(b) Relative values of FWHM in different primary spherical aberration systems under different working wavelengths

3 超振荡望远系统成像分析

非相干成像系统对强度是线性且空间不变的，并且系统的强度脉冲响应是振幅脉冲响应模的平方[38]。因此当使用非相干光照明时，像强度Iim(X,Y)是强度脉冲响应|h(X,Y)|2和理想像强度Ig(X,Y)的卷积，表示为[39]：

其中，h(X,Y)是振幅脉冲响应。

为验证超振荡望远系统超越衍射极限的分辨力，本文使用532 nm 平面波垂直照明物体，在透镜半径为4 mm，焦距为1000 mm 的情况下，根据瑞利判据可知衍射受限望远系统的分辨极限为81.1 μm。本文采用三缝结构作为目标物，中心距为55.148 μm，大约是瑞利判据的0.68 倍，单个狭缝长度是2 倍瑞利判据。图6 是不同望远系统对三缝结构的成像结果，系统视场均为1.5 倍瑞利判据。图6(a)为衍射受限望远系统对三缝目标物的成像，可知其无法分辨；图6(b)表明超振荡望远系统能够清楚地分辨三缝，成像对比度为0.153。对比结果表明，超振荡望远系统具备超越衍射极限成像的能力。其视场受限问题可考虑采用视场拼接方法实现大视场超分辨成像。

图6 不同望远系统对三缝结构的成像结果。(a) 衍射受限望远系统对三缝结构的成像结果；(b) 超振荡望远系统对三缝结构的成像结果；(c) 红线和蓝线分别为(a)和(b)的中心竖直截面强度分布Fig.6 Imaging results of the three-slit struct in different telescopic systems.(a) The imaging result of the three-slit struct in the diffraction limited telescopic system;(b) The imaging result of the three-slit struct in the super-oscillatory telescopic system;(c) The red and blue lines are the intensity distribution of the central vertical section of (a) and (b),respectively

为研究超振荡望远系统中不同初级球差对像的影响，在该系统出瞳处加入不同RMS 值的初级球差，成像结果如图7 所示。在532 nm 的工作波长下，初级球差的RMS 值分别是(a) 0.01λ、(b) 0.025λ、(c) 0.042λ时，超振荡望远系统针对三缝目标物体的成像结果，其中心竖直截面的像对比度分别为0.1587、0.1702、0.152，像与视场内最大强度的比值(像的相对强度)逐渐降低。对于入射光的窄波带成像效果，图8 给出工作波长分别是(a) 527 nm、(b) 537 nm 时，无球差超振荡望远系统针对三缝目标物的成像结果，可知其中心竖直截面的像对比度分别为0.0798、0.0817，和532 nm 工作波长的成像结果相比，对比度有所下降。图8(c)中工作波长为527 nm 和537 nm、无球差时系统强度点扩散函数与中心点的比值几乎相同，所以成像结果的中心竖直截面相对强度几乎一样。

图7 (a)-(c) 分别为RMS 值为0.01λ、0.025λ、0.042λ 的初级球差超振荡望远系统对三缝结构的成像结果；(d) 红、蓝、黑线分别为(a)、(b)、(c)的中心竖直截面强度分布Fig.7 (a)-(c) Imaging results of the three-slit struct in the super-oscillatory telescopic system with primary spherical aberrations which RMS values are 0.01λ,0.025λ and 0.042λ,respectively;(d) The red,blue and black lines are the intensity distribution of the central vertical section of (a),(b),and (c),respectively

4 分析

为研究球差对超振荡望远系统成像细节的影响，从零开始逐渐增加初级球差的RMS 值，记录不同RMS 值下局部视场中的成像结果，并计算中心竖直截面的像对比度，确定系统容许的极限RMS 值，从而指导光学系统的设计。图9 是工作波长分别为527 nm、532 nm、537 nm 时，不同初级球差超振荡望远系统对三缝结构的成像对比度，图中虚线位置表示对比度为0.153。

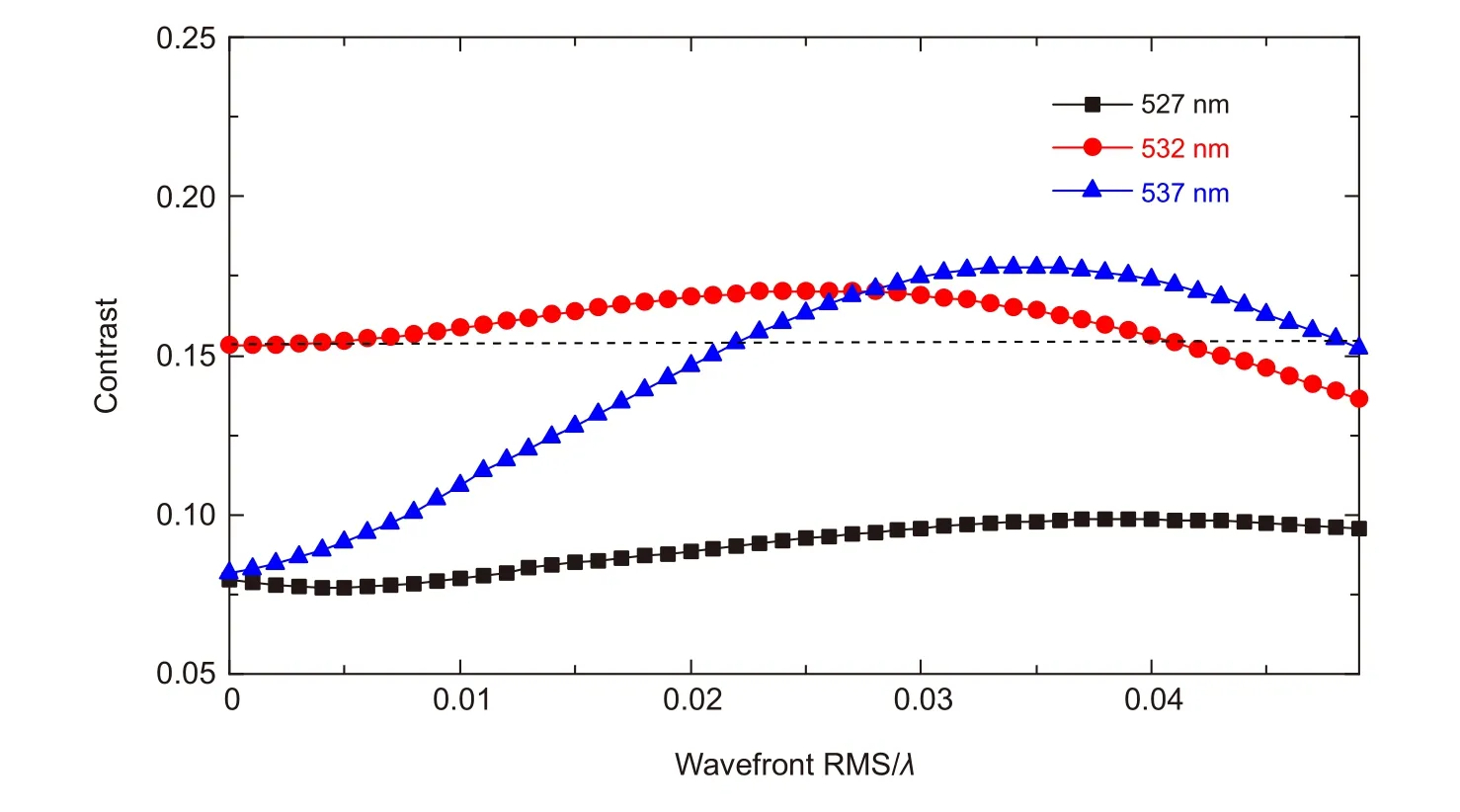
图9 不同初级球差，不同工作波长下，超振荡望远系统中像的中心竖直截面对比度Fig.9 With different spherical aberrations,the contrast of the central vertical section of the image in the super-oscillatory telescopic system under different working wavelengths

由图8(c)可知，当初级球差的RMS 值等于0，即不考虑球差的影响时，532 nm 工作波长下对比度明显高于527 nm 及537 nm 工作波长对比度。这是源于SO 仅在532 nm 的工作波长下才能实现恰好为π的相位差，其他工作波长下相位差将改变，此时强度点扩散函数不再满足预设的约束条件。因此若相位调制结构能够满足对于一定范围内任意工作波长均能实现精准的π 相位差，就能避免不同工作波长对成像效果的影响，即消色差超表面。

由图9 可知，532 nm 工作波长下望远系统成像对比度在RMS 值为0.025λ时达到最大值0.1702。虽然考虑较小球差时系统成像中心对比度有所增加，但此时视场周围光强较高，影响目标物体边缘位置处的成像效果，如图7 中所示。满足对比度高于0.153 的前提下，超振荡望远系统最大容许RMS 值为0.041λ的初级球差，尽管此时视场有限，但可通过视场拼接等方式扩大视场范围。如果初级球差的RMS 值高于0.041λ，该系统将无法分辨中心距为0.68 倍瑞利判据的目标物。527 nm 工作波长下望远系统成像对比度在RMS 值变化范围内始终小于0.153，其原因在于该工作波长下成像对比度随RMS值的变化较小。0.04λ处对比度最大为0.0986，意味着该波长下在任意初级球差范围内都无法分辨目标物体。537 nm 工作波长下望远系统成像对比度随着RMS 值增加有所提升，在0.022λ处成像对比度超过0.153，能够分辨目标物体，且随着RMS 值继续提升，对比度在0.035λ处达到峰值0.1779。该工作波长下，RMS 值在0.022λ到0.048λ范围内，均能满足对比度高于0.153。

由此可知，工作波长的不同、球差的大小对超振荡望远系统成像的影响，其本质都是改变了出瞳面光场相位，导致相位差不再为π，从而影响成像质量。

5 结论

本文分析了超振荡望远成像系统中球差的影响，并以初级球差为例计算出容许范围。该超振荡望远成像系统依据超振荡理论及线性规划的优化思想设计，在532 nm 工作波长下，最高可分辨中心距为0.68 倍瑞利判据的三缝结构。构建了伴随球差的超振荡望远系统强度点扩散函数的数学模型，基于该模型精确得出了容许的初级球差RMS 极限值为0.041λ。同时分析了窄带工作波长527 nm、537 nm与不同初级球差共同作用于该系统的成像结果。该模型在光学测量、环境监视、超分辨望远等领域具有潜在的应用前景。