基于BP神经网络的电力无人机抗干扰屏蔽罩优化设计

郭 昊，刘书山，刘兰兰，徐 溧，肖乔莎，陈 彬*

(1.智能带电作业技术及装备(机器人)湖南省重点实验室，湖南 长沙 410100；2.带电巡检与智能作业技术国网公司实验室，湖南 长沙 410100；3.国网湖南省电力有限公司超高压输电公司，湖南 衡阳 421002；4.三峡大学 电气与新能源学院，湖北 宜昌 443002)

0 引言

随着输电线路规模的不断增大,故障率随之增高,为了保证输电系统的稳定运行,带电作业成为解决输电线路故障的必要手段。随着无人机(Unmanned Aerial Vehicle,UAV)在电网系统中的大规模使用,利用无人机解决输电线路故障成为趋势,例如无人机高空安全监护、清理输电线路异物、清洗绝缘子串等[1-2]。无人机在执行上述任务的过程中需靠近输电线路,但此时会受到导线发出的无线电干扰而影响其正常工作,确定合理的屏蔽措施将提高无人机抗干扰能力,能更好地保障输电线路稳定运行。因此,对电力无人机的抗干扰屏蔽罩展开研究具有重要的工程应用价值。

国内外学者针对电力无人机的研究较多,但主要集中在无人机电磁场避障策略[3-4]、输电线路故障检测[5]等方面,针对电力无人机的飞行安全主要考虑使无人机与输电线路保持一定距离,并未从无人机本身出发,提高其抗干扰能力。文献[6]通过电磁场仿真计算出距输电线路不同方位处的无人机机身电场和磁场,根据无人机电磁场保护阈值来确定无人机的电磁防护安全距离。但当无人机执行带电作业任务需靠近输电线路时,必须提高其抗干扰能力。目前,提高无人机抗干扰能力的主要措施是施加屏蔽罩,文献[7]分析了强电磁辐射下无人机的电磁耦合路径和毁伤效应,针对无人机的光电系统、天线端口及机体部分分别给出了施加屏蔽网栅、高性能导电膜及孔洞类屏蔽罩的方法,但该研究只停留在理论阶段,并未将上述方法具体应用到无人机上验证其可行性。文献[8]为了研究无人机外壳的屏蔽效能,基于数值仿真计算了电磁波辐射方向对无人机内部电磁场分布的影响,得到了无人机壳体的屏蔽效能随屏蔽材料的电导率和磁导率的变化规律,但未考虑无人机外壳的散热开孔对其屏蔽效能的影响。对无人机施加屏蔽罩必须考虑不同散热开孔结构对其屏蔽效果的影响,并针对屏蔽罩的孔缝结构进行优化,求解出满足无人机抗扰度阈值的设计方案。对于屏蔽罩的结构优化问题,目前尚未有文献针对电力无人机展开研究,但在绝缘子电场屏蔽方面,文献[9]通过有限元计算屏蔽罩对交流盆式绝缘子表面电场分布的影响,将屏蔽罩的设计变量进行多项式拟合,并采用遗传算法对屏蔽罩结构进行优化,求解出屏蔽效果最佳的设计方案,该研究对电力无人机抗干扰屏蔽罩的优化设计具有一定参考意义。

针对上述问题,首先对输电线路的无线电干扰场强进行计算,通过矩量法求解无人机屏蔽前的受干扰程度。然后建立屏蔽罩的三维仿真模型,对比不同材料及开孔形状屏蔽罩的屏蔽效果并确定其优化参量,通过正交试验并结合仿真计算出不同结构参数下屏蔽罩后的无人机内部场强。最后,通过BP神经网络对上述数据进行训练和预测,确定屏蔽罩的最佳设计方案,并通过仿真验证其屏蔽效果。

1 无人机带电作业无线电干扰水平

要计算出无人机带电作业无线电干扰水平,首先需要通过模拟电荷法计算出输电线路表面最大电场强度,进而根据无线电干扰频谱特性公式计算出输电线路附近的无线电干扰场强。以导线周围无线电干扰场强计算结果为激励源,通过矩量法仿真计算出输电线路对无人机的无线电干扰水平。

1.1 基于模拟电荷法的导线表面最大场强求解

国际无线电干扰特别委员会推荐的交流输电线路无线电干扰场强计算的经验公式可用于直接求解与基准点位于同一水平面的无线电干扰。基准点的定义为:距输电线路边相导线的水平距离为20 m,距地高度为2 m的点,根据该经验公式可计算基准点的无线电干扰场强为[10]:

E0=3.5Emax+12r-30,

(1)

式中:E0为基准点的无线电干扰场强,单位dB(μV/m);Emax为输电导线表面最大电场强度,单位kV/cm;r为导线半径,单位cm。

由式(1)可知,要求得基准点的无线电干扰场强首先需求解出输电导线表面最大电场强度。目前,在输电线路电场计算中常用的方法包括有限元法、矩量法、边界元法及模拟电荷法等,相比之下,模拟电荷法计算原理简便、实用性强,只需设置模拟电荷的类型、数量及位置,即可通过数值计算公式求解场域内任意一点的场强[11]。通过模拟电荷法求解输电导线表面最大场强的运算流程如图1所示。

图1 模拟电荷法运算流程Fig.1 Operation flowchart of charge simulation method

求解得到模拟电荷值后,可计算出输电导线表面的平均电场强度Ea为[12]:

(2)

式中:Qi为相导线上的模拟电荷,单位C;n为导线的分裂数,ε0为真空介电常数,r为导线半径,单位cm。

输电导线表面的最大电场强度Emax为:

(3)

式中:R1为分裂导线的外接圆半径,单位cm。

1.2 输电线路无线电干扰场强求解

国际无线电干扰特别委员会根据全世界范围的统计结果归纳出输电线路的无线电干扰频谱特性和横向特性,表示为[10]:

(4)

式中:E为与基准点同一水平面上某点的无线电干扰场强,单位dB(μV/m);f为无线电干扰频率,单位MHz;d1为该点距输电线路边相导线的距离,单位m。

根据式(4)可计算出与基准点位于同一水平面,即距地高度为2 m的平面内任意一点在不同频率下的无线电干扰场强。但无人机执行带电作业任务时,与输电线路近似位于同一高度,因此,要计算无人机在执行带电作业任务时受到的无线电干扰,需先求解出与输电线路位于同一高度上其辐射的无线电干扰场强。由式(4)计算得到的地面端无线电干扰场强,可根据电磁波在空气中的传播损耗反演求出线路端输电导线辐射的无线电干扰场强。根据弗里斯传输公式可得电磁波在空气中的传播损耗为[13]:

(5)

式中:L为电磁波自由空间损耗,单位dB;Pt为发射点电磁波功率,单位dBm;Pr为接收点电磁波功率,单位dBm;d2为传播距离,单位km。

由于电磁波在空气中的传播损耗是以功率计算的,因此需要将式(4)计算得到的无线电干扰场强转化为功率。当辐射点与辐射源之间的距离为R时,辐射点的功率密度Pd为[14]:

(6)

式中:P(W)为辐射点的功率,单位W;R为辐射点与辐射源之间的距离,单位m。

若以电场强度表示辐射点的功率密度,则:

(7)

式中:E(V/m)为辐射点的电场强度,单位V/m;Z0为自由空间的特性阻抗,取值为120π。

将式(6)和式(7)联立求解可得:

(8)

为了与式(4)和式(5)中的无线电干扰场强及辐射功率的单位相对应,可将式(8)转化为:

(9)

式中:E为无线电干扰场强,单位dB(μV/m)。

将式(9)代入式(5)可求得线路端发射的电磁波功率Pt为:

(10)

根据式(9)可计算出线路端无人机所在位置处的无线电干扰场强Et为:

(11)

式中:R2为无人机距离输电导线之间的距离,单位m。

若将Et以V/m为单位表示,则:

(12)

以某500 kV输电线路为例,导线水平排列,对地高度为31 m,导线采用四分裂导线,分裂间距为40 cm,半径为1.75 cm,相间距为10 m,输电线路产生的无线电干扰频率在0.15～10 MHz[15],当无人机与输电导线位于同一高度且与导线之间的水平距离为1 m时,根据式(12)可求出不同频率下无人机所在位置处的无线电干扰场强,如图2所示。

图2 不同频率下无线电干扰强度Fig.2 Radio interference intensity at different frequencies

由图2可知,输电线路产生的无线电干扰频谱主要分布在0.15～4 MHz,当频率大于4 MHz时,无线电干扰场强较小,接近于0,与文献[16]结论一致,验证了本文无线电干扰场强求解方法的正确性。

1.3 无人机带电作业无线电干扰仿真计算

无人机在执行带电作业任务时受到的无线电干扰超过阈值时,其内部电子元器件因起晕或拉弧会导致性能降低或丢失,甚至造成坠机事件[17]。为了保证无人机正常工作,国家标准规定,民用轻小型无人机辐射抗扰度阈值不应超过10 V/m[18]。为了探究输电线路产生的无线电干扰对无人机内部电子元器件的干扰程度,选取电网常用的大疆御2行业进阶版无人机作为研究对象,该型无人机具有机身轻巧、定位精准及支持六向避障等优点,机身使用碳纤维复合材料,尺寸为322 mm×242 mm×84 mm,其实物如图3(a)所示。通过三维实体模拟软件建立其三维仿真模型如图3(b)所示。

(a)无人机实物

(b)仿真模型

为了探究无人机距离上述某500 kV输电线路1 m处受到的最大干扰,选择输电线路产生的无线电干扰最大值,即频率为2.7 MHz,无线电干扰场强为443.4 V/m的情况进行仿真。仿真基于FEKO软件进行,求解方法为矩量法[19],采用平面波辐照的方式,设置平面波幅值为443.4 V/m,方向在0°～360°,观测点位于无人机内部,可得到平面波不同辐射方向下无人机内部场强的方向图如图4所示。

由图4可知,无人机在执行带电作业任务的过程中距离输电线路为1 m时,其内部场强超过国家标准规定的无人机抗扰度阈值。因此,为保证无人机正常工作,需对无人机施加屏蔽罩。

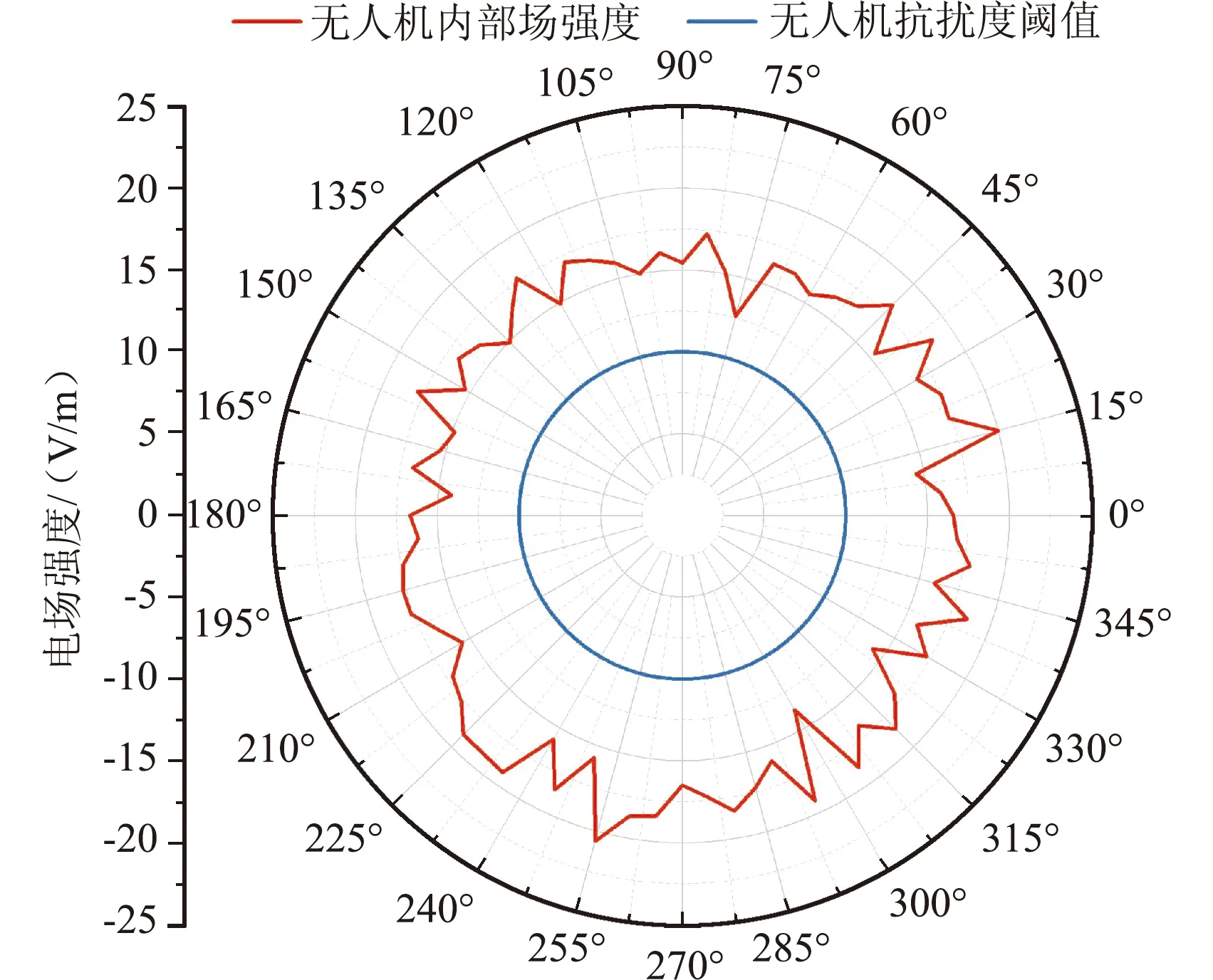
图4 无人机内部场强方向Fig.4 Field strength pattern inside UAV

2 电力无人机屏蔽罩设计

2.1 屏蔽罩设计参量的确定

采用屏蔽罩可以降低输电线路对无人机的无线电干扰,屏蔽罩的屏蔽效果与屏蔽罩的材质及散热开孔的个数、形状、间距等因素有关。金属材料在电导率、磁导率性能方面具有优势,是实现电磁屏蔽的主要材料。典型的金属屏蔽材料包括金、银、铜、铝、纳米晶及坡莫合金等[20],但由于金、银、铜等材质屏蔽罩造价昂贵,在实际工程中应用较少,故本文主要对比铝、纳米晶及坡莫合金的屏蔽效果,上述3种材料的参数如表1所示。

考虑到无人机旋翼与机身之间的距离,设置屏蔽罩与无人机机身之间的距离为5 mm,屏蔽罩厚度为1 mm,开孔形状为方形,散热开孔面积为5 000 mm2,开孔数量为60,建立无人机屏蔽罩仿真模型如图5所示。

图5 无人机屏蔽罩仿真模型Fig.5 Simulation model of UAV shield

与上述仿真类似,将无人机屏蔽罩仿真模型导入FEKO软件中,设置平面波幅值为443.4 V/m,在0.15～10 MHz施加上述3种材料屏蔽罩后无人机内部场强如图6所示。

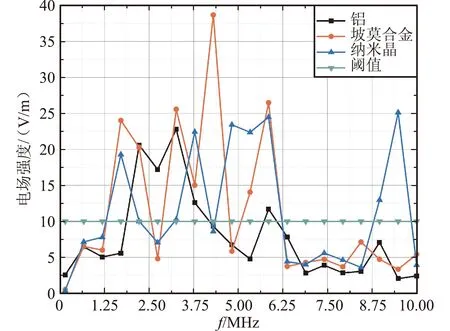
图6 不同材料屏蔽效果对比Fig.6 Comparison of shielding effects of different materials

综合对比上述3种材料的屏蔽效果可知,铝型材屏蔽罩的屏蔽效果比其余2种好,故确定电力无人机抗干扰屏蔽罩的材质为铝。

不同散热开孔形状对无人机屏蔽罩的屏蔽效果影响较大[21],因此,对比分析圆形、方形及长方形开孔形状的屏蔽效果,保持上述3种形状的开孔面积相同,经仿真得到不同开孔形状的屏蔽效果如图7所示。

图7 不同开孔形状屏蔽效果对比Fig.7 Comparison of shielding effects of different opening shapes

由图7可知,屏蔽罩采用方形开孔时,其屏蔽效果比其余2种好,故选择电力无人机抗干扰屏蔽罩的散热开孔形状为方形。另外,无人机屏蔽罩的屏蔽效果还与散热开孔的数量n、孔缝与屏蔽罩边缘的间距d1及孔缝间距d2有关,其示意如图8所示。开孔数量的变化会导致开孔大小、孔缝间距发生改变,但需保证开孔面积保持不变。

图8 屏蔽效果影响因素示意Fig.8 Schematic diagram of factors affecting shielding effect

屏蔽后的无人机内部场强与屏蔽罩的结构参数d1、d2、n之间是一种多维非线性函数映射关系,上述结构参数的取值范围较为宽泛,依靠穷举法很难确定屏蔽效果最佳的设计方案。神经网络具有强大的多维非线性映射能力,对解决此类结构优化问题具有一定的优势。神经网络模型通过学习和训练输入/输出数据即可得到输入与输出之间的多维非线性特性[22],从而建立屏蔽罩结构参数与无人机内部场强之间的关系。因此将d1、d2、n作为电力无人机屏蔽罩的设计变量,通过神经网络确定屏蔽效果最佳的方案。

2.2 基于正交试验的屏蔽罩结构设计

神经网络模型需要一定的样本数据进行训练,从而得到输入与输出之间的多维非线性特性,因此首先需要通过FEKO仿真得到不同屏蔽罩结构参数下的无人机内部场强以供神经网络训练。为了使样本数据具有代表性,从而提高神经网络模型的准确性,采用正交试验法来确定仿真方案。

在满足屏蔽罩外形尺寸的约束下,确定不同正交方案下d1、d2的取值为10、15、20、25、30、35、40 mm,n的取值为60、80、100、120、140、160、180。根据正交试验原理[23],可采用三因素七水平正交试验方案来探究不同屏蔽罩结构参数与无人机内部场强之间的关系,正交试验方案及结果如表2所示。

由表2可知,屏蔽罩散热开孔的结构参数对屏蔽效果的影响较大,不同结构参数下无人机内部场强最大差异可达83.55%。上述结构参数取值下无人机内部场强均大于10 V/m,超过无人机抗扰度阈值,因此还需进一步优化屏蔽罩的开孔结构。

续表

3 基于BP神经网络的屏蔽罩结构优化

3.1 BP神经网络的基本原理

BP神经网络是模仿人或动物神经元网络的运行方式而建立的数学模型,具有非线性映射、自主学习及自组织适应性等优势,在各学科领域得到广泛应用[24]。BP神经网络主要由神经元通过权重连接而成,包括输入层、隐层及输出层3层结构,其结构如图9所示。

图9 BP神经网络模型结构Fig.9 Structure of BP neural network model

BP神经网络包括正向传播和反向传播2个流程。正向传播流程首先由输入层神经元对不同结构参数下无人机内部场强进行读取并传递至隐层神经元,隐层神经元对接收到的数据进行转换处理并传递到输出层。当训练输出与实际数据的误差超过预期时,开始进入反向传播流程,输出层作为初始端,使用误差下降法对每层上的误差权值和阈值进行修正并传播至隐层和输入层[25]。当训练输出与实际数据误差减小到期望值以下或到达最大迭代次数后结束训练,得到屏蔽罩结构参数与无人机内部场强之间的多维非线性映射关系。最后,通过BP神经网络预测不同屏蔽罩结构参数下的无人机内部场强。BP神经网络的运算流程如图10所示。

图10 BP神经网络运算流程Fig.10 Operation flowchart of BP neural network

训练输出与实际数据误差e的计算公式定义如下:

●用有机硅功能肥与硅谷农科院培育的“硅谷829”高产小麦新品种，在2017年试验田亩产达到974公斤，创中国小麦历史最高纪录。

(13)

式中:d(k)为实际数据的输出,y(k)为训练输出,n为样本数据的组数。

输入层与隐层权值ωih的更新公式为:

(14)

式中:hi为隐层输入,r为神经网络学习速率,x为输入样本数据,ωoh为隐层与输出层的权值。

隐层与输出层权值ωoh的更新公式为:

ωoh=ωoh+rhie。

(15)

输入层与隐层阈值bh的更新公式为:

(16)

隐层与输出层阈值bo的更新公式为:

bo=bo+e。

(17)

3.2 屏蔽罩优化结果及屏蔽效果分析

为了验证BP神经网络模型的准确性,以上文通过正交试验得到的49组仿真结果作为样本数据,令其中第7、13、19、25、31、37、43组作为预测的验证数据,其余作为训练数据。设置BP神经网络的输入层节点数为3,隐层节点数为5,输出层节点数为1,可得BP神经网络的训练输出如图11所示,预测输出如图12所示。

图11 BP神经网络训练输出Fig.11 Training output of BP neural network

由图12可知,BP神经网络的预测数据与原始数据之间的最大误差为5.26%,平均误差为2.04%,验证了BP神经网络模型预测的准确性。

图13 不同结构参数下无人机内部场强Fig.13 Internal field strength of UAV under different structural parameters

由图13可知,当d1=17 mm、d2=12 mm、n=140时,无人机内部场强最小为3.89 V/m,小于无人机抗扰度阈值。为了验证无人机抗干扰屏蔽罩按照上述结构进行散热开孔的屏蔽效果与未屏蔽前类似,在2.7 MHz设置平面波幅值为443.4 V/m,方向为0°～360°,观测点位于无人机内部,可得到平面波不同辐射方向下屏蔽后无人机内部场强的方向图,如图14所示。

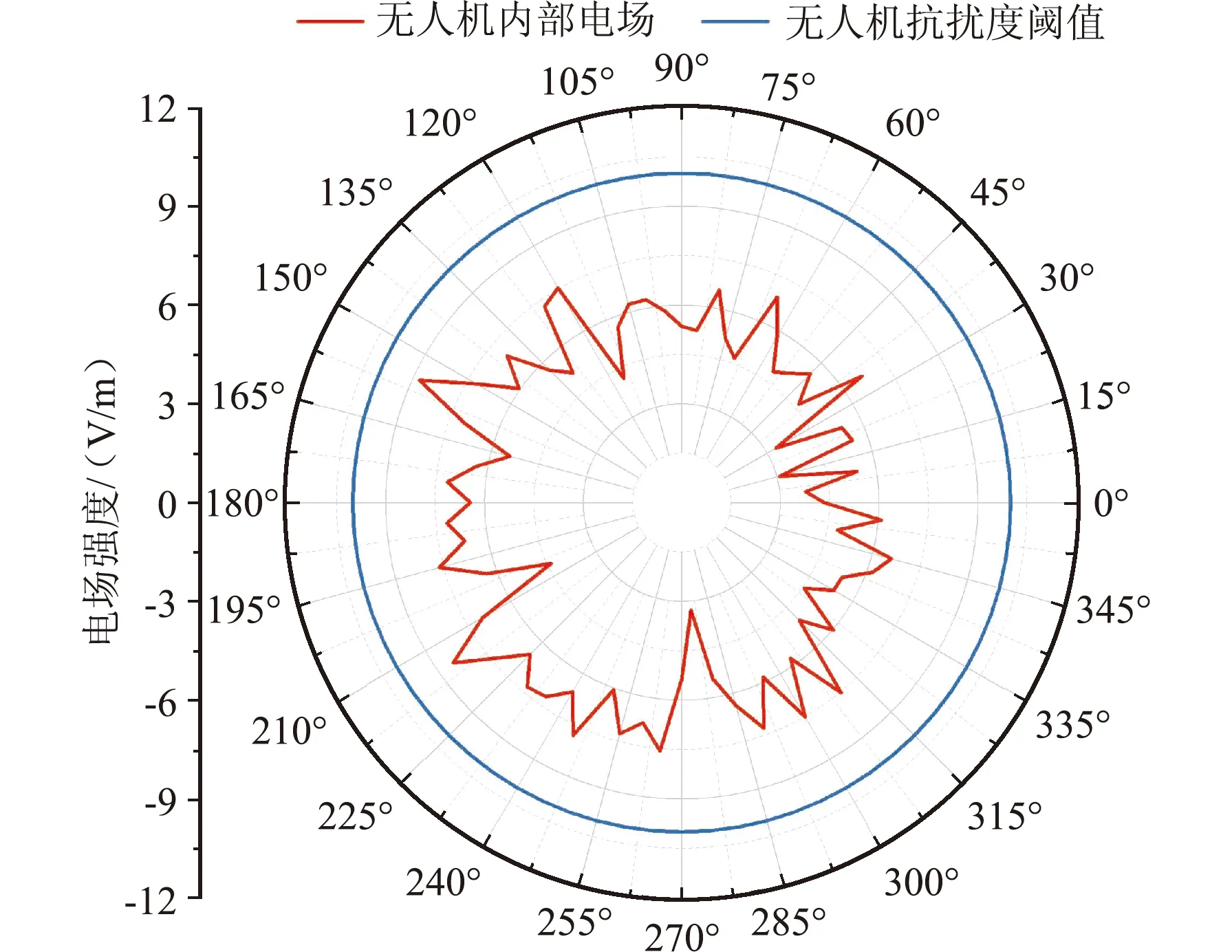
图14 屏蔽后无人机内部场强方向图Fig.14 Field strength pattern inside UAV after shielding

由图14可知,不同平面波入射方向下屏蔽后的无人机内部场强均小于无人机抗扰度阈值,当平面波入射角度为155°时无人机内部场强最大。提取出该入射方向下屏蔽罩表面感应电流分布云图,如图15所示。

图15 屏蔽罩表面感应电流分布云图Fig.15 Cloud chart of induced current distribution on the surface of shield

由图15可知,屏蔽罩表面感应电流分布较为均匀,开孔未导致其表面感应电流路径的剧烈变化,开孔方式符合要求。为了探究不同频率下屏蔽后的无人机内部场强大小,按照图2所示的不同频率下输电线路无线电干扰场强施加辐射源,得到不同频率下屏蔽后无人机内部场强如图16所示。提取出无人机施加屏蔽罩前后其周围电场分布云图如图17所示。

由图16和图17可知,在0.15～10 MHz屏蔽后的无人机内部场强均未超过无人机抗扰度阈值, 施加屏蔽罩后无人机周围电场减小,电力无人机抗干扰屏蔽罩的设计满足要求。

图16 不同频率下屏蔽后无人机内部场强Fig.16 Internal field strength of UAV after shielding at different frequencies

(b)施加屏蔽罩

屏蔽罩在削弱输电线路对无人机产生的无线电干扰的同时还应保证不屏蔽无人机的控制信号。大疆御2行业进阶版无人机的通信频率为2.4 GHz,无人机天线位于脚架位置,遥控器发射功率为26 dBm,根据式(9)可得,遥控器的发射场强为0.12 V/m,将其作为平面波辐照的幅值,通过FEKO仿真可得2.4 GHz下无人机屏蔽前后天线接收场强的方向图如图18所示。

由图18可知,在部分方向下屏蔽后无人机天线接收场强小于屏蔽前,但屏蔽前无人机天线接收场强的最小值为66.51 mV/m,屏蔽后所有方向下无人机天线接收场强均大于该值,因此,文中所设计的屏蔽罩不会影响无人机正常通信。

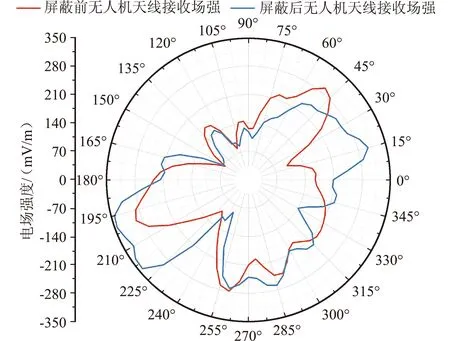
图18 2.4 GHz下屏蔽前后无人机天线接收场强Fig.18 Receiving field strength of UAV antenna before and after shielding at 2.4 GHz

4 结论

本文对电力无人机抗干扰屏蔽罩进行优化设计,得到主要结论如下:

①当无人机与输电线路之间的水平距离为1 m时,根据弗里斯传输公式反演计算得到在2.7 MHz下输电线路无线电干扰场强最大为443.4 V/m。

②屏蔽罩的散热开孔结构参数对屏蔽效果的影响较大,相同材料及开孔形状下,不同结构屏蔽罩的屏蔽效果最大差异达到83.55%。

③通过BP神经网络优化了无人机抗干扰屏蔽罩散热孔缝的结构,当d1=17 mm、d2=12 mm、n=140时屏蔽效果最佳;通过仿真验证了按上述结构设计的屏蔽罩在不同方向、不同频率下无人机内部场强均未超过无人机抗扰度阈值,满足国家标准的规定,所设计的屏蔽罩不会影响无人机的正常通信。本文的研究对于保证无人机带电作业的安全及提高电力无人机的抗干扰能力具有一定的参考意义。