基于卷积神经网络的空间导航信号抗干扰处理技术

王春霞，刘新芳

(闽南科技学院 光电信息学院，福建 泉州 362332)

0 引言

卫星导航综合了传统导航系统的优点,真正实现了各种天气条件下全球高精度被动式导航定位,能够对地面、海洋、空中和空间用户进行导航定位。随着卫星导航精度的不断提高,对空间导航信号的抗干扰性能也提出了更高的要求,在强烈的电磁干扰和环境干扰背景下,空间导航信号的传输和有效检测受到限制,需要构建优化的空间导航信号抗干扰模型,通过建立空间导航信号抗干扰模型,进行空间导航信号的优化控制,构建空间导航信号的优化采样和信道均衡控制模型,提高空间导航信号传输系统的优化管理能力,相关的空间导航信号抗干扰技术研究受到人们的极大关注[1]。

空间导航信号抗干扰设计是建立在对空间导航信号滤波处理的基础上,结合对空间导航信号的特征提取和波束控制,进行空间导航信号检测,提高空间导航信号的抗干扰能力[2]。文献[3]方法研究导航信号频域干扰抑制方法及其FPGA实现,基于快速傅里叶变换的干扰抑制算法对频域干扰抑制方法进行了研究。文献[4]方法研究基于动态聚类的卫星导航信号多波束抗干扰方法,基于k均值聚类算法的动态指向多波束抗干扰方法建立天线阵列进行导航信号多波束抗干扰。但上述方法进行空间导航信号抗干扰处理的输出信噪比不高,信号检测性能不好。针对上述问题,本文提出基于卷积神经网络(Convolutional Neural Network,CNN)的空间导航信号抗干扰技术。首先构建空间导航信号的卫星传感采样模型,对采集的空间导航信号进行波束聚焦和信号增强处理,提取空间导航信号的时频相关性特征量。之后采用CNN滤波器进行空间导航信号的滤波处理,实现空间导航信号增强和抗干扰处理。最后进行仿真测试分析,结果表明了本文方法在提高空间导航信号抗干扰能力方面具有优越性能。

1 空间导航信号模型及均衡调度

1.1 空间导航信号采样模型

为了实现基于CNN的空间导航信号抗干扰处理,需要首先构建空间导航信号的卫星传感采样模型,对采集的空间导航信号进行信号增强和融合滤波,采用阵元误差稳健性分析的方法,得到空间导航信号分布模型[5],采用待检测单元统计特性分析方法,得到空间导航信号的频谱宽度ν(t,θ):

(1)

式中:*表示复共轭算子,m为待检测单元参数,M为待检测单元,t为空间导航信号频谱,θ为空间导航信号宽度,xi为空间导航信号滤波,wi为采样导航信息值。

采用空时自适应处理处理的方法,建立空间导航信号的卫星传感器采集模型,得到传感器基阵为:

(2)

式中:H表示归一化多普勒频率分布的复共轭转置,x(t)和ω(θ)分别为空间导航信号的天线安装角的偏差和相位角。在阵面轴向方向,得到空间导航信号的模糊函数w(t),可以表示为:

w(t)=[x(t)]T-[ω(θ)]T,

(3)

式中:T为模糊参数。

在先验分布出现偏差时,通过多维阵列参数融合的方法,得到卫星接收的回波信号的时延尺度为:

τ0(θ)=Δsinθ-c,

(4)

式中:c为方位角和距离变化的联合估计参数,Δ为信号增量。

考虑距离模糊的影响,得到空间导航信号的时频项[6]。信号中的孔径损失是因为发射信号时发射阵元与接收信号时接收阵元的方位向天线方向图存在间隔,在近距离处会导致收发阵元的波束不能完全重叠,从而使有效合成孔径长度减小,造成合成孔径的损失。阵元误差是阵元的位置出现偏差现象,对此,针对孔径损失以及阵元误差进行联合调节,以此得到空间导航信号的非平稳时间序列模型为:

(5)

式中:ci(n)和ui(n)为空间导航信号的平稳序列下的相位角和偏差角,j为孔径损失序列,n为误差控制参数,p为孔径损失参数值,q为阵元误差参数,k为阵元误差序列,Φij为导航距离范围取值,Θik为模糊时频值。

根据俯仰空域导向矢量调节模型,得到空间导航信号的非平稳时间序列输出为:

(6)

(7)

式中:gM为导航信号输出值,(θi)si为信号阵列参数。

通过上述对空间信号模型构建,得到空间导航信号的采样模型如图1所示。

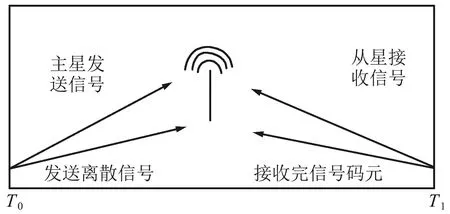
图1 空间导航信号的采样模型Fig.1 Sampling model of space navigation signal

由图1可以看出,本文方法采用主星进行离散信号的发送,利于从星对信号进行接收,实现空间导航信号的采样。

1.2 导航信号传输的等间隔均衡调度

在上述构建了卫星传感采样模型的基础上,进行空间导航信号的多维空间参数识别[7]。在二维平面(m,n)上进行空间导航信号的信道均衡调度,建立空间导航信号的阵元误差补偿模型,采用离散采样和自适应均衡调度的方法,进行空间导航信号的模糊优化控制[8],基于最小二乘准则的方法,得到空间导航信号的奇异值分布为:

(8)

式中:xk为导航信号的半数均衡数值,yk为导航信号的调度参数。

当ωk满足n个空间导航信号的输出稳态特征分布集时,信号表示为:

(9)

式中:θk为离散误差值。考虑阵元脉冲域的时间间隔固定。

采用代价函数g(x,y)作为空间导航信号的阵元误差调节函数,得到空间导航信号的奇异特征分解模型为:

(10)

式中:Tk为特征向量函数值。

利用阵元脉冲域的模糊辨识参数模型,设定导航信号传输的等间隔均衡调度的步长为:

(11)

式中:λ为间隔模糊辨识度。

根据上述分析,对导航信号传输进行等间隔均衡调度,在此基础上实现卫星的抗干扰处理并进行优化。

2 卫星导航信号抗干扰处理优化

CNN是一种前馈神经网络,它的人工神经元可以响应一部分覆盖范围内的周围单元,对于信号处理有出色表现。基于上述经过均衡调度的信号,对其进行抗干扰处理优化,根据信号的频谱特征收敛性进行信号补偿和滤波抑制,采用CNN滤波器进行空间导航信号的信号滤波处理[9],得到空间导航信号滤波的CNN分类模型为:

(12)

式中:N为滤波参数,j为孔径损失序列,Cn为信号补偿值。

通过融合聚簇特征分析方法,进行空间导航信号传输系统等间隔信息融合和优化调度,建立空间导航信号的信道容量分析模型[10-11],得到信道容量:

(13)

式中:an为信号的交叉分布特征量,n为容量参数。进行空间导航信号抗干扰设计,得到空间导航信号的信道参数分布集为x(k-1),…,x(k-M)[9]。

构建空间导航信号传输系统的信道自适应聚类参数分析模型,通过模糊参数识别,得到空间导航信号重建的冲击函数为:

(14)

式中:bv为信道自适应值,Xv为冲击向量。

在此基础上,建立空间导航信号的杂波抑制模型[12],空间导航信号的滤波处理过程描述为:

① 随机选择空间导航信号滤波的初始量Wk。

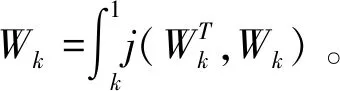
根据上述分析,采用模糊信息加权的方法,得到提取空间导航信号的随机分布谱特征量[15-17],以y(k)y*(k)为最小化的约束函数,*表示复共轭,采用CNN进行信号滤波增强的优化学习训练,CNN模型如图2所示。

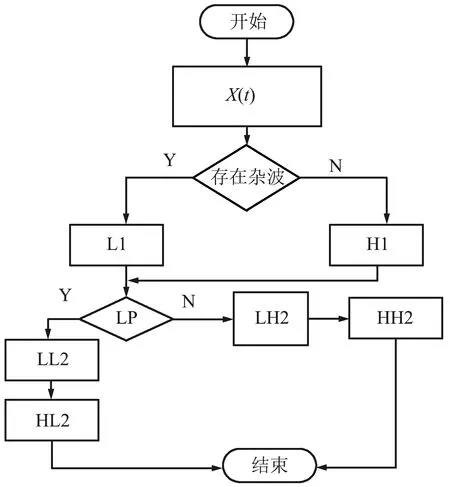
图2 CNN模型Fig.2 CNN model

3 仿真测试

3.1 信号测试实验

为测试本文提出的空间导航信号中的信道时变特征估计方法的性能,在Matlab软件内,采用本文方法进行仿真实验,主要仿真参数如表1所示。

表1 主要仿真参数Tab.1 Main simulation parameters

图3为观测数据,观测时间与采样频率分别为100 s和5 120 Hz。

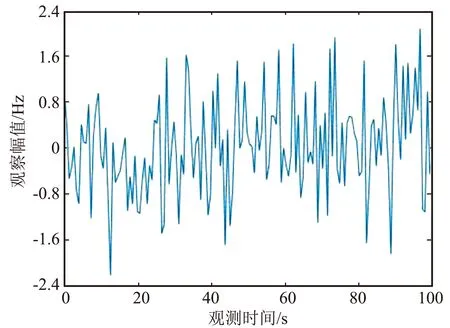
图3 观测数据Fig.3 Observed data

3.2 应用实验

设定空间导航信号的采样时间间隔为1.5 ms,伪码长度为1 023,伪码速率为1.023 MHz,空间导航信号的杂噪比设为60 dB,干扰信噪比为-12 dB,工作波长为1.3 m,原始的空间导航信号波形如图4所示。

图4 原始的空间导航信号波形Fig.4 Original space navigation signal waveform

以图4的空间导航信号为输入,进行空间导航信号抗干扰处理,并与文献[3]方法和文献[4]方法进行对比,得到抗干扰输出如图5所示。

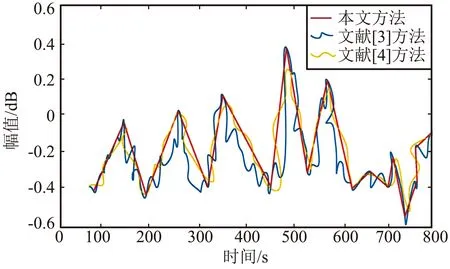
图5 空间导航信号抗干扰输出Fig.5 Anti-jamming output of space navigation signal

分析图5得知,本文方法能有效实现空间导航信号的抗干扰处理,信号的纯度得到提升,而对比方法的信号仍具有干扰,说明本文方法抗干扰效果较好。

测试输出信噪比,采用蒙特卡罗试验,得到对比结果如表2所示。

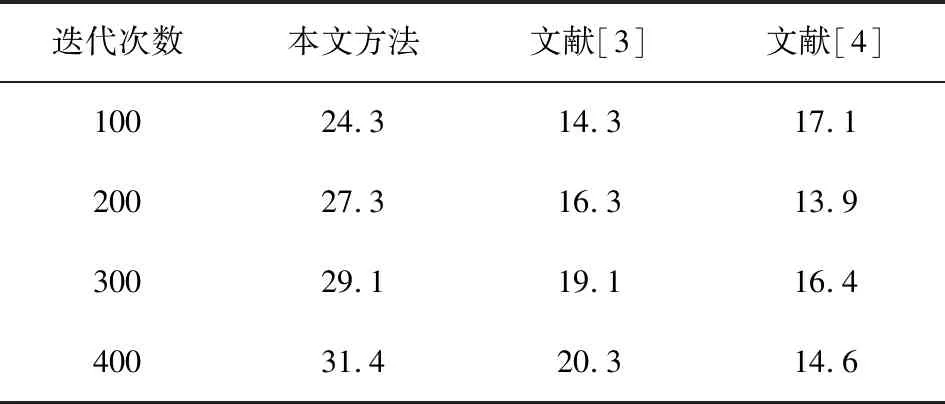
表2 空间导航信号抗干扰处理后的输出信噪比Tab.2 Output signal-to-noise ratio of space navigation signal after anti-jamming processing 单位:dB

分析表2可知,本文方法进行空间导航信号抗干扰处理的输出信噪比较高,而文献[3]方法与文献[4]方法的信噪比明显低于本文方法,说明本文方法能够有效提升信号的抗干扰滤波性能。

4 结束语

构建优化的空间导航信号抗干扰模型,通过建立空间导航信号抗干扰模型,进行空间导航信号的优化控制,本文提出基于CNN的空间导航信号抗干扰技术。对采集的空间导航信号进行信号增强和融合滤波,采用离散采样和自适应均衡调度的方法,进行空间导航信号的模糊优化控制,采用CNN滤波器进行空间导航信号的信号滤波处理,实现空间导航信号增强和抗干拢设计。分析得知,本文方法进行空间导航信息抗干扰处理的输出信噪比较高,信号纯度得到提升。