一种基于信息熵的级联式新类识别方法

曾文玺, 董育宁

(南京邮电大学通信与信息工程学院, 江苏 南京 210003)

0 引言(Introduction)

在常见的闭集假设中,传统机器学习(Machine Learning,ML)已取得显著的成效[1]。但是,现实场景已不再是简单的静态环境,这大大削弱了现有方法的鲁棒性,因此新类检测(Novel Class Detection,NCD)问题成为网络流分类的重要挑战之一。

针对开放环境的问题,目前ML中有一种解决方案是基于极值理论(Extreme Value Theory,EVT)[2]的方法。BALASUB-RAMANIAN等[3]将EVT与ML中的随机森林(Random Forest,RF)相结合,基于每个已知类Weibull分布的累积概率识别新类。本文在南邮数据集和ISCX数据集两个数据集上进行了实验验证,分类精度只有85%左右,并且由于需要对不同的已知类类别分别进行拟合,并判断是否拒绝拟合,导致预测时间较长。

上述方法未能很好地解决ML中的NCD问题,其分类准确率有待提高且不满足在线分类的速度要求。因此,本文提出一种基于信息熵的级联式新类识别(Entropy based Cascade NCD,EntC-NCD)方法用于改善以上问题,并将其与现有代表方法进行了对比。

1 相关工作(Related work)

目前,针对NCD问题,研究人员从生成模型(Generative Model,GM)和判别模型(Discriminative Model,DM)两个不同的角度进行探索,并取得一定成果。现有的方法主要有基于距离、基于支持向量机(Support Vector Machine,SVM)和基于EVT的方法。

在基于距离的方法研究中,MU等[4]基于孤立树异常检测算法[5]的思想提出了基于完全随机树的无监督学习算法(SENCForest);武炜杰等[6]则是在SENCForest基础上融入了k近邻,不仅提高了在异常区域内搜索新类的准确率,也降低了系统开销。

基于SVM的方法是由SCHEIRER等[7-8]首次应用到NCD中,首先提出1-vs-Set模型,再进一步使用非线性内核融入EVT,提出了基于Weibull校正的SVM(W-SVM)模型;针对W-SVM中所有的已知类具有相同阈值的问题,JAIN等[9]又引入了概率开放集SVM(Probabilistic Open Set SVM,POS-SVM),该分类器可以对每个已知类采用不同的拒绝阈值,从而达到提高分类准确率的效果。

基于EVT拟合分布的方法如今被广泛使用,除了前文提到的W-SVM;BALASUBRAMANIAN等[3]则是提出了基于投票的极值理论模型(Vote-Based EVT,V-EVT),通过结合RF拟合已知类别样本的投票分布,得到逐类的Weibull分布。通过对应的Weibull分布计算其累积概率,根据阈值判断是否为已知类。

受V-EVT思路的启发,本文选择传统ML中分类效果较好的RF模型,与评估不确定性的信息熵相结合,提出基于信息熵的新类检测方法,想要达成的目标是在保证较高分类准确率的同时,克服需要多次计算Weibull累积概率导致分类耗时较长的问题。

2 本文方法(The proposed method)

基于信息熵和RF的NCD方法的模型框架如图1所示,主要分为训练、校准和测试三大模块。其中:训练集只包含已知类样本,校准集包含已知类和少量伪新类样本,测试集包含全部已知类和新类样本;训练集按照3∶7的比例随机分为D1和D2两个部分,D1训练多分类器RF1;θ为新类判别阈值;β为异常流样本置信度阈值。

图1 基于信息熵和RF的NCD方法的模型框架Fig.1 Model framework of NCD method based on information entropy and RF

2.1 基于信息熵的新类发现方法

RF投票的分布中含有较多信息,投票的分散程度反映出分类器对样本的不确定性。当训练样本的类别ci∈Ck={c1,c2,…,cn}时,若测试样本的类别ci∉Ck,分类器对其判决的不确定性会远高于类别ci∈Ck的测试样本。据此引入信息熵作为评估不确定性的标准,并作为已知类和新类的分类依据。

为了验证这一想法,以ISCX数据集为例,随机抽取7个类作为已知类训练集和测试集,另外3个类作为新类测试集,分别测试并统计已知类和新类的信息熵分布[10]。

根据RF的投票结果计算样本信息熵的方法如下:首先将样本d判为已知类ci的树的数目占树总数的比例作为样本d属于已知类ci的概率,其次计算样本d被判为每个已知类的概率,并由此计算样本d的信息熵,计算已知类概率和信息熵的方法分别如公式(1)和公式(2)所示:

(1)

(2)

其中:Ib(ci|d)∈{0,1}是第b棵树判断样本d是否为类ci的结果,若判为ci,则设为1,否则为0;B为RF中树的总数目,n为已知类的类别数。

ISCX数据集的信息熵分布统计结果如图2所示。已知类的信息熵值明显聚集于小于1的区域内,而新类的信息熵则普遍较大,这为基于信息熵的新类检测提供了可行性。

图2 已知类和新类信息熵分布统计Fig.2 Information entropy distribution statistics for known and novel classes

2.2 去除异常流样本

在实际网络的流传输过程中会产生异常流样本,从而降低分类器学习的准确性。因此,训练前需筛选出训练集中的异常样本,具体步骤如表1中的算法1所示;得到干净的已知类样本训练集Dt和异常样本数据集Do,并用Dt训练新类分类器RFn。

表1 去除异常流样本算法

测试集中同样会存在异常已知类样本,因此分类器对其判定的不确定性会增大,使该样本的信息熵增大,容易被误判为新类。

为此,从Dt中抽取与Do数量相等的样本集Dp,Do和Dp分别作为正、负样本训练去异常点二分类器RFo。测试阶段通过级联RFo,对RFn认定的新类样本进行再分类,删除其中的异常已知类样本。

2.3 确定新类判别阈值

依据校准集选取新类的判别阈值,校准数据集Dv中包括全部已知类和少量伪新类的样本;用RFn进行预测,计算各个样本的信息熵,并以0.1为区间分别统计已知类和新类的信息熵分布,取两个分布的交点作为新类判别阈值θ,具体过程表2中的算法2所示。

其中:hi表示[i-0.05,i+0.05);Khi、Uhi分别表示已知类和新类样本的信息熵在hi区间内的样本数量;Ck、Cu分别表示已知类、新类;I(hi,Ck|d)∈{0,1}表示若d∈Ck且Hd∈hi,则I(hi,Ck|d)等于1,否则为0。

2.4 分类模型

如上文所述,测试集中异常样本的信息熵比正常样本高,导致误判为新类。因此,采用级联模式进行二次筛选。经过RFn分类后,信息熵小于等于θ的样本被认定为已知类,并直接输出RFn的分类结果;而信息熵大于θ的样本,称其为候选新类(包含新类和已知类中的异常样本)。

对于候选新类样本通过级联的去异常点二分类器RFo进一步判断,并引入异常置信度ACon,计算公式如下:

(3)

其中:Co表示异常类;Ib(Co|d)∈{0,1}表示若第b棵树判断样本d∈Co,则Ib(Co|d)等于1,否则为0。

同时,引入异常置信度阈值β用于判断,对于异常置信度大于阈值β的样本,判为异常点,从候选新类中删除,反之则判为新类。本文方法完整的测试过程表3中的算法3所示。

表3 新类-异常样本检测算法

其中:θ为算法2中获取的新类判别阈值,β为异常置信度阈值,可以灵活调节以平衡分类的准确率和覆盖率;Hd为根据多分类器分类结果计算的信息熵;ACon(Co|d)为根据RFo得到的异常置信度;yu和yo分别表示预测标签为新类和异常点。

3 实验(Experiment)

3.1 实验环境

实验使用惠普笔记本电脑,硬件和软件的配置如下:CPU为AMD R5-4600H@3.00 GHz,GPU为NVIDIA GTX 1650 Ti-4G,16 GB运存,操作系统为64位Windows 10;在Python编程语言环境下运行。

分类器均采用RF,树的数目设置为100棵,叶节点最小样本数设置为1个,所有实验采用五折交叉验证。

3.2 评估指标

3.2.1 新类分类指标

采用分类准确率Ao作为分类准确性指标,定义如下:

(4)

其中:TPi、TNi、FPi、FNi分别代表已知类的真阳性、真阴性、假阳性、假阴性,TU、FU分别代表新类的正确判断和错误判断,n为已知类类别数目。

采用F1值作为评估指标,由精确率P和召回率R计算得出,计算公式如下:

(5)

需要注意,计算F1时未将新类作为一个额外的样本类加入计算,因为在分类器中,没有新类的训练样本,所以将新类作为一个真阳性分类没有意义。但是,在计算已知类的P和R时,FP和FN中也会包含错误分类的新类样本。

3.2.2 滤除异常样本指标

本文方法包含从候选新类样本中过滤异常样本的模块,准确率仍然使用Ao,但是样本总数减少。因此,定义覆盖率指标Coverage如下所示:

(6)

其中:N表示预测样本总数,Nn表示判为异常样本的数目。

定义ORR(Outlier Removal Rate)表示已知类异常样本的滤除率、FDR(False Deletion Rate)表示新类样本被判为异常点的比例。

3.2.3 时间性能指标

分别用Tt和Tc表示训练时间和分类时间,单位为ms/样本,分别表示逐样本的平均训练时间和分类时间。

3.3 数据集

使用南邮数据集(NJUPT Dataset,NDset)、ISCX数据集进行方法验证。NDset是通过WireShark于2020年在南京邮电大学校园网环境下采集的[11]。NDset和ISCX数据集的具体类别和样本数如表4和表5所示。

表4 南邮数据集

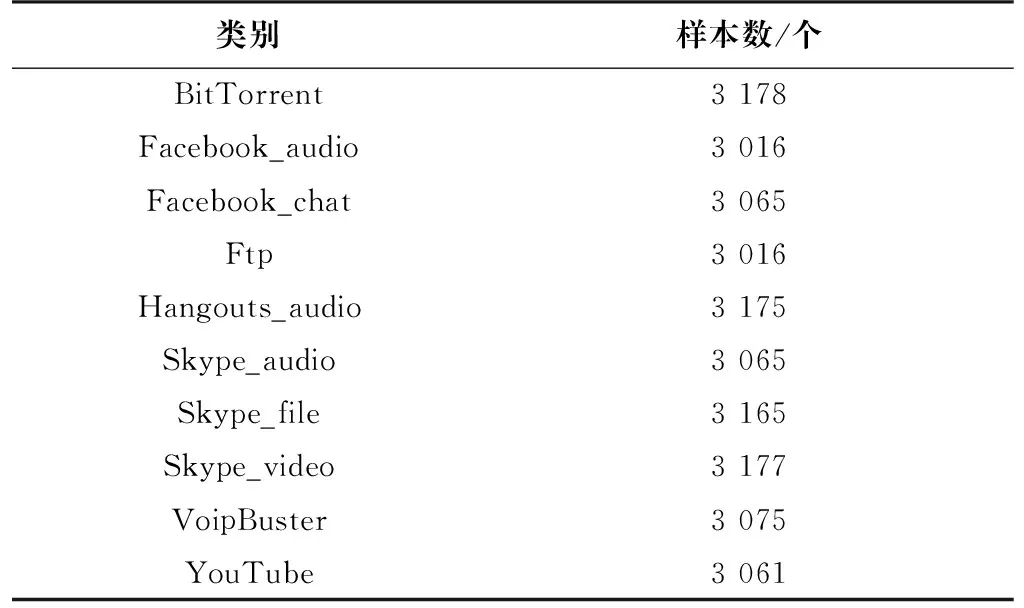
表5 ISCX数据集

3.4 不同置信度异常阈值对比

为了验证级联式去除异常样本模块的有效性,以NDset为例,新类类别选取为[1080P_douyu,1080P_huya,720P_tencent,QQ_music]共4类,校准数据集Dv选取的伪新类为1080P_huya。通过修改阈值β对比去除异常点前后的各项评估指标的变化,结果如表6所示,β=1表示未做去除异常点处理。

在未进行去除异常点的情况下,6 330个已知类测试样本中有1 133个被新类识别模块判为候选新类,约占所有已知类测试样本的17.9%,而4 910个新类测试样本被判断为候选新类的个数为4 856个,约占比98.9%。级联去异常点模块后,β使用0.5时,会有66.3%的已知类异常样本被删除,而新类中有18.5%的样本被当作异常样本被误删。表6中的数据表明,去异常点模块能从候选新类样本中删除大部分的已知类异常样本,并且保留大多数新类样本,进一步提高新类样本的纯度,并且可以根据需要自行调节阈值。需要注意,F1没有跟随阈值变化是因为R和P的计算中未包含判为候选新类的样本。

3.5 不同新类分类阈值对比

根据本文提出的算法2,计算得到一个新类分类的阈值,会对于分类的最终性能有着较强的影响,因此设置实验通过修改θ值进行对比,验证其有效性。新类和校准集选取同本文“3.4”小节,根据算法2得到阈值θ为0.9,阈值β统一设置为0.5,不同θ的性能对比结果如表7所示。

表7 不同θ的性能对比

当θ取0.9时,覆盖率比θ取1.1时小1.3%,但准确率高1%,F1值也高2.4%;而相比于θ取0.7时,准确率几乎一样,但覆盖率高2.3%,只有F1值低0.6%且θ取0.9时,对新类样本的误删率最低。因此,由算法2计算的阈值θ的分类性能较好。

3.6 不同方法的性能对比

将本文方法EntC-NCD与文献方法V-EVT分别在NDset和ISCX两个数据集上进行实验对比,采用本文所提方法进行去异常点处理时,阈值β分别设置为0.5、0.8,结果如表8和表9所示,EntC-NCD-1表示未做去异常点处理。

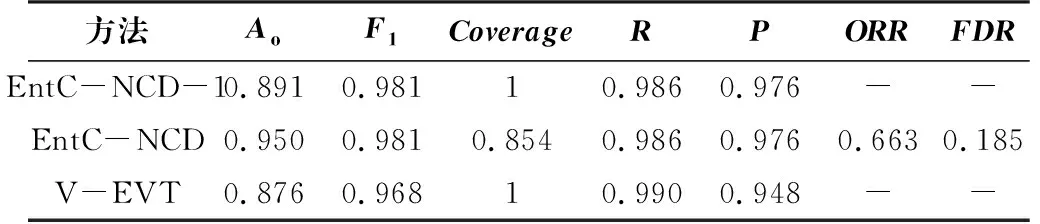
表8 不同分类方法在NDset上的对比结果

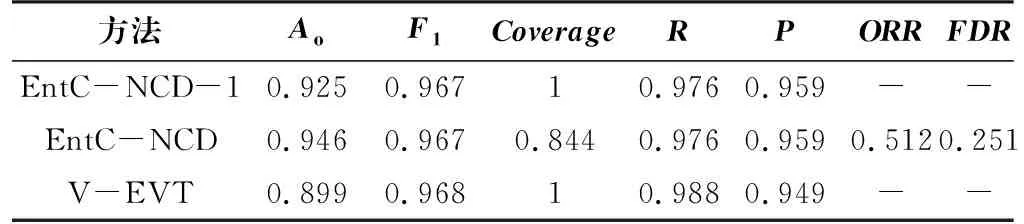
表9 不同分类方法在ISCX数据集上的对比结果

在两个数据集上,EntC-NCD-1比V-EVT的Ao高1.5%～2.6%;F1则是在ISCX数据集上两者相似,在NDset上是本文所提方法较优;EntC-NCD通过去除异常点处理,进一步提高了分类准确率,其Ao高于V-EVT方法4.7%～7.4%。V-EVT是通过RF投票数分布拟合每个已知类的Weibull分布,再通过计算测试样本的累积概率判断是否属于该类;若不属于所有已知类,则判为新类。但是,实际的拟合结果并不完全贴合实际投票的分布,导致V-EVT的分类性能不如本文所提方法。

在不同数据集上的时间性能对比结果如表10所示。EntC-NCD只需要进行一次多分类并计算一次信息熵,预测时间较短,在NDset上,即使加上去异常点处理,平均一个样本也仅需0.079 ms;V-EVT虽然只需要进行一次分类器分类,但是需要分别计算每一个已知类的Weibull分布值进行判断,所以需要0.592 ms,分类时间仍较本文所提方法高一个数量级。

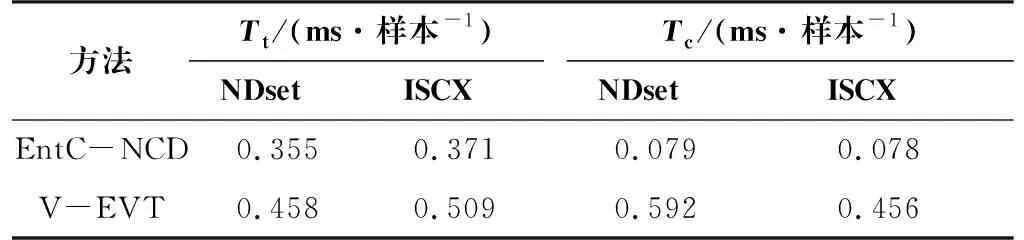
表10 不同分类方法的时间性能对比结果

在训练时间上,EntC-NCD需要多训练一个去异常点分类器,V-EVT则是需要拟合每一个已知类的Weibull分布,训练耗时相差不大。

综上所述,相比于V-EVT,本文方法在不同的数据集上均有更好的表现,同时具有一定的普适性。

4 结论(Conclusion)

本文提出了一种基于信息熵的级联式新类识别和去异常点模型,并针对新类分类阈值的选取给出了优选方法。此外,本文还讨论了不同新类判别阈值、异常置信度阈值对分类性能的影响,在两个真实的网络数据集上对本文所提方法进行验证,并与文献方法进行对比。实验数据表明,本文所提方法的识别准确率均可达到约95%,单个样本的识别时间仅需0.079 ms,在分类精度和时间性能上均优于对比方法且有一定的普适性,更加适用于不同需求的新类分类场景。