基于多元加权中心特征的高速公路网韧性研究

林培群,刘子豪, 闫明月

(1. 华南理工大学 土木与交通学院,广东 广州 510640;2. 交通运输部 路网监测与应急处置中心,北京 100005)

0 引 言

2019年国家交通运输部印发《国家综合立体交通网指标框架》,明确设置 “交通网韧性”指标。同年,中共中央、国务院印发的《交通强国建设纲要》中也明确提出,要提升运输网络系统弹性,建设高质量现代化综合立体交通网。为了构建韧性高速公路运输系统,如何量化区域封闭对高速路网韧性的影响成为亟待研究的问题。为此,需要基于实际路网拓扑特征与道路流量,对不同管控措施下的高速公路网络进行韧性评估与量化分析[1]。

高速公路网络符合复杂网络的基本特征。近年来,随着网络科学理论的不断发展,国内外众多学者结合复杂网络针对航空、城市轨道、公交等运输网络进行了大量研究。吴丽娜等[2]构建了应用连通度、连通平均值等无权拓扑指标,对省域高速公路连通可靠性进行了分析;翁小雄等[3]以收费站作为节点,建立了高速公路多层复杂网络模型,对珠江三角洲地区高速公路进行分析;郑义彬等[4]使用P空间方法建立了湖北省高速公路无权网络,并对其中心性及鲁棒性进行了研究,但孤立看待各节点中心性指标,没有融合节点多元特性;焦柳丹等[5]在介数中心性等无权拓扑指标基础上,融入客流及站点属性,基于变异系数法与VIKOR方法对重庆轨道交通重要节点进行了实证分析。

在高速公路网韧性研究方面,代洪娜等[6]考虑流量权重定义了概率介数指标评价节点与路段的重要性,并以局域高速公路网进行了仿真分析;杜佳昕等[7]使用流量数据对拓扑路网中介数中心性指标进行加权修正,对实际交通路网脆弱性进行了分析,但仅考虑了单一节点中心性指标;温振国[8]采用对偶映射法,以高速公路为节点,分析了陕西省高速公路网复杂特性及鲁棒性,但忽略了区县间的连通关系;周涛等[9]采用L空间方法构建无权路网,融合传统静态拓扑中心性指标与PageRank算法挖掘高速路网中重要节点,但未考虑道路流量的动态特征;王晚香等[10]利用对偶法构建高速路网拓扑结构,构建了行程时间可靠性模型,对局域高速路网进行分析,但忽略了真实道路流量。

现有文献在高速公路网络(高速路网)的韧性分析上取得了一定成果,但仍存在以下几点不足:① 现有研究大多以收费站、高速公路为节点构建路网拓扑结构,较少考虑高速公路网络中行政区县之间的连通关系;② 现有研究多以城市中局部路网区域进行分析,聚焦于全省及以上范围的高速路网分析不足,较少融合实际的高速客货车辆流量构建加权网络;③ 现有研究大多孤立分析各节点中心性指标,忽略了节点多阶邻域下的联系性,没有融合多元特性挖掘高速路网中的重要节点。

鉴于此,笔者以广东省高速公路网络为研究对象,采用P空间映射方法将路网中的收费站归并到所属区县并融合高速公路收费流水等数据,构建加权网络,分析基本拓扑特征;基于真实道路流量,对传统无权网络中心度量指标进行修正;结合多元特征引力模型(multi-characteristics gravity model),考虑节点多阶邻域的影响力,对全省高速路网重要节点及通道进行识别;设计适用于加权网络的网络韧性评价指标,采用随机攻击策略与基于中心性指标的蓄意攻击策略,通过4种封闭措施下的仿真模拟,对全省高速路网韧性进行分析,技术路线如图 1。研究结果可为识别高速路网中重要节点提供新的视角,为量化区域封闭对高速公路的连通性影响提供参考。

1 问题描述与建模

1.1 高速公路流量加权网络建模及特性

高速路网是典型的复杂网络,路网的静态拓扑结构对网络韧性有重要影响。同时高速路网上的客货车流量是网络节点之间联系的动态特性,为综合分析高速路网的韧性水平,需要将客货车流量集成到网络拓扑结构构建加权网络。目前常用的交通网络拓扑结构映射方法主要有L空间映射法和P空间映射法[11]。其中L空间映射法是将路网中的交叉口、重要枢纽节点以及收费站节点等抽象为连通图中的节点,能够直观反映路网布局;P空间映射法将属于同一线路上的所有节点成对连接,更能体现线路之间中转的便捷程度。然而传统的P空间映射法构建的是无权网络拓扑结构,仅反映了网络的几何属性,节点之间流量能反映运输经济特征。因此,需要在无向无权网络上融入真实道路流量,将收费站点归并到所属区县中,以区县为基本节点,将属于同一条高速公路的区县节点进行连接,构建加权网络G=(I,H,W)。其中,点集I为全省收费站点所属的区县级行政区划;边集H为属于同一高速路线区县节点之间的连边;W为各连边H中的流量权重。

1.1.1 高速公路加权网络特性

高速公路加权网络整体特征指标包含节点度、加权度分布与网络平均距离。在连通网络中,节点i的邻边数量为该节点i的度:

(1)

式中:Aij为该网络图的邻接矩阵的元素;N为节点数量。

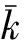
对于加权网络,需要考虑节点之间的连接权重。节点i的加权度如式(2):

(2)

式中:si为加权度;wij为区县节点i与j之间连边的权重,即客货车流量;ni为与节点区县i存在连边的区县集合。

将网络中节点i与节点j之间通过边数最少的路径定义距离dij,网络的直径定义为所有距离dij中的最大值。对于高速公路网络,距离长度意味着从区县i到区县j需要经过不同高速公路的最少边数,能够体现全省高速路网的整体运输效率。网络平均距离U定义为所有节点对之间距离的平均值,平均距离U越小,说明两个区县之间的行程需要转换线路的次数越少,路网连接效率越高。

(3)

1.2 高速公路加权网络中心性度量方法

在复杂网络结构中,节点中心性体现在不同维度,中心值较高的节点对维持网络的连通性起到关键作用,准确识别核心节点是网络韧性分析的前提。笔者基于复杂网络理论,选取度中心性、介数中心性、接近中心性、特征向量中心性作为基础指标,通过客货车流量进行修正,构建适用于加权网络的中心性度量指标。为避免单一中心性指标的局限性,引入k核值与邻域半径,构建多元中心引力模型,对网络节点中心性进行综合评价。

1.2.1 加权度中心性

度中心性D一般指网络度中心性,对于文中高速公路加权网络而言,衡量高速路网中区县节点的重要性不仅需要考虑几何空间上的重要性,同时还要考虑客货运输通道中的重要性。因此,将节点加权度中心性Di定义如式(4):

(4)

式中:si为节点的加权度;Wall为网络的所有连边流量权重之和,通过节点的加权度与全局流量的比例对传统度中心性指标进行修正。

1.2.2 加权介数中心性

节点介数能够反映节点在网络中的联络与中转作用,一个节点i的介数中心性Bi定义为全网络中所有节点对之间的最短路径经过节点的次数。对于加权网络,考虑节点之间的交互强度,计算公式如式(5);对于连边而言,其加权介数中心性定义如式(6):

(5)

(6)

式中:σ(u,t)为所有节点对(u,t)之间的最短路径数量;σ(u,t|i)为所有节点对之间最短路径经过节点i的数量;υu,t为u和t之间的流量。

1.2.3 加权接近中心性

接近中心性C是连通网络中节点i到其他所有节点最短距离平均值的倒数。接近中心性值越高,表明该节点到其他所有节点的平均距离越短,充分体现该节点到达其他节点的便捷程度。对于加权网络,通过节点的点权度与全局流量的比例对传统接近中心性指标进行修正,计算公式如式(7):

(7)

1.2.4 加权特征向量中心性

节点特征向量中心性不仅考虑该节点的邻居节点数量,同时也考虑邻居节点的重要程度。对于表征网络的加权邻接矩阵Z,存在特征向量X,使得ZX=λX,不同特征向量对应不同的特征值λ。根据Perron-Frobenius定理[12],中心性测度需要的是最大特征值所对应的特征向量,当且仅当X为最大特征值λmax所对应的特征向量时,其各项分量为正,通过幂迭代算法可以得到该特征向量,其中第i个分量xi即为区县节点i的加权特征向量中心性。

1.2.5 多元特征引力模型

识别复杂网络中有影响力的节点是网络科学中聚焦的热点问题。大量实验表明,仅考虑节点单一特征来可靠地识别有影响力的节点是不够的。多元特征引力模型(MCGM)是一种基于引力定律的影响力度量模型[13],有效地集成了节点的多种特征,考虑邻居的数量、邻居的影响、节点的位置及节点之间的路径信息,衡量节点在动态扩展中的影响力。因此,笔者基于该方法对构建的高速公路加权网络中心节点进行综合评价。

根据复杂网络理论,节点度中心性Di,表示节点的相对邻居数量;节点特征向量中心性Ei,既可以反映邻居数量,也可以反映每个邻居的影响程度;节点k核值Sk反映其在网络中的深度,一个图的k核是指反复去掉度值小于k的节点及其连线后,所剩子图的节点大小,若一个节点属于k核,而不属于k+1核,则该节点核度为k。就个体而言,度值、k核值以及特征向量中心性值较大的节点影响更大。将节点度值、k核值和特征向量中心性值之和作为节点的质量,将两个节点之间的最短距离作为节点之间的距离,因此,节点i的影响力可以通过式(8)进行估计:

(8)

式中:R为邻域半径(图2),R一般取[d],其中d为网络平均距离,该网络初始R取值为2;Di、Ski、Ei由于量纲不相同,需要进一步进行归一化处理,将式(8)改写为:

(Dj/Dmax+Skj/Sk,max+Ej/Emax)

(9)

而相比于度值D和E中心性,k核值空间较小,值空间越大的指数,中位数与最大值的比值一般越小,归一化k核指数仍大于另外两个指数。因此需要进一步降低k核指数的影响,引入系数α:

(10)

式中:Emid、Sk,mid分别表示度值、特征向量中心性值以及k核值的中位数,而分子中取最大值的作用是防止k核指数作用被过度削弱,最后将节点i的多元特征影响力定义为:

(Dj/Dmax+αSkj/Sk,max+Ej/Emax)

(11)

多元特征引力模型的求解步骤如下:

步骤1输入加权连通网络图G=(I,H,W)和节点邻域半径R。

步骤2计算每个节点i∈I的加权度中心性Di。

步骤3计算每个节点i∈I的加权特征向量中心性Ei。

步骤4计算每个节点i∈I的k核值Ski。

步骤5分别计算Dmax、Emax、Sk,max、Dmid、Emid、Sk,mid以及修正系数α。

步骤6对于i∈N,找到每个节点i在邻域半径R范围内所有邻居节点j,通过式计算节点i的M中心值。

步骤7得到基于多元特征引力模型下的节点中心性序列。

1.3 高速公路加权网络韧性评估方法

PAN Shouzheng等[14]将交通网络韧性定义为系统受到干扰或中断下交通网络的连通状况及保持可接受服务水平的能力。现有研究常用网络连通性指标评估网络韧性,并未考虑区域之间的客货车流量分布与需求特性。因此,笔者对传统的最大连通子图比例以及全局连通效率进行流量强度加权修正,作为韧性评估指标。

1.3.1 最大加权连通子图比例

当高速路网中某个节点或某条通道因突发事件进行管控或交通封闭时,会对初始网络的正常运输连通性产生影响。笔者将最大加权连通子图比例定义为式(12):

(12)

(13)

式中:L(G′)为节点封闭后剩余网络中的最大连通图大小;L(G)为初始网络最大连通图大小;γ为节点封闭后的最大连通图G′承接的道路总流量与初始网络G承接的道路总流量的比例。当γ为0时,表明该剩余网络并不是承担运输流量的核心路网,此时路网的运输服务能力受到最大程度的影响。反之当γ=1时,说明剩余网络是核心运输区域,路网的运输服务能力并未受到影响。

1.3.2 加权网络全局连通效率

网络的全局连通效率定义为所有节点对之间最短距离倒数的平均值,对于笔者构建的高速公路加权网络,计算节点对连通效率时,还需要考虑节点对(i,j)所承担的流量占比,如式(14):

(14)

式中:υi,j为节点对(i,j)之间的流量。若节点i无法到达j,同时节点对(i,j)所承担的流量较大,则当前网络的实际运输连通效率受到较大影响。

2 实例应用与分析

以广东省高速公路网为研究对象,使用全省成熟的运输业务系统所积累的2021年4月份全样本高速公路收费数据、收费站信息数据以及区县地理信息数据。其中收费数据主要字段包括收费站出入口编号、入站出站时间、车辆类型代码、车辆行驶里程等。收费站信息数据主要字段包括收费站编号、收费站名称、高速公路编号、高速公路名称、收费站经度纬度等。区县地理信息数据主要字段包括区县名称、区县所属地市、区县覆盖面积及中心经纬度等。采用P空间映射法构建出的广东省高速公路复杂网络共有120个节点,对部分区县(如南澳县未连通高速公路)以及收费站位置偏移较大的数据进行清洗,修正后网路共有116个节点,存在617条连边,如图 3。

2.1 网络整体特征分析

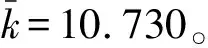
考虑2021年4月份实际道路客、货车流量,由式(2)计算得到各节点加权度,97.39%的区县客车流量加权度低于20万辆/d,95.65%区县货车流量加权度低于3万辆/d。以客车流量为例(图 5),以大湾区为核心的“十字型”高速路网联系廊道较为明显,粤港澳大湾区城市群的区县点权度较高,体现出较强的交通集聚效应。由大湾区通往到粤北、粤东、粤西通道的区县形成“十字型”廊道式分布:粤北从清城区到连州,粤东从博罗县到梅县,粤西从高要到徐闻,基于客流与货流的节点加权度能够挖掘全省高速路网中的骨干区县。

2.2 网络中心性分析

以客车流量加权高速网络为例,根据式(4)～式(11)计算路网各节点中心性。以度中心性为例,图6将传统度中心性D′与加权度中心性D进行对比,对于仅考虑静态拓扑特征的传统度中心性,各区域差异较小,而加权后的度中心性更能挖掘全省高速路网的核心区域。客车流量Di、Bi、Ci、Ei、Mi等级排名情况如表 1。由表1可知,东莞市、白云区、宝安区等级最高,属于高速路网中的核心区位,紧随其后的是中山市、顺德区、龙岗区、南海区、番禺区、南山区、花都区等区域。各中心性指标与2021年各地市、区县GDP总值的Pearson相关性系数如表2。由表2可知,各中心性指标与GDP平均相关系数为0.607,呈明显线性正相关,M与其他4个中心性指标高度相关,平均相关系数为0.850,验证了指标的有效性。省界边缘区县如连山县、仁化县、封开县、潮南区、澄海区、阳西县等区县中心性较低,与高中心性区县衔接程度低。全省高速公路客车出行量集中在粤港澳大湾区中,其中广州、深圳、佛山以及东莞4个地市集聚效应显著。

表1 各中心性下前9名节点序列

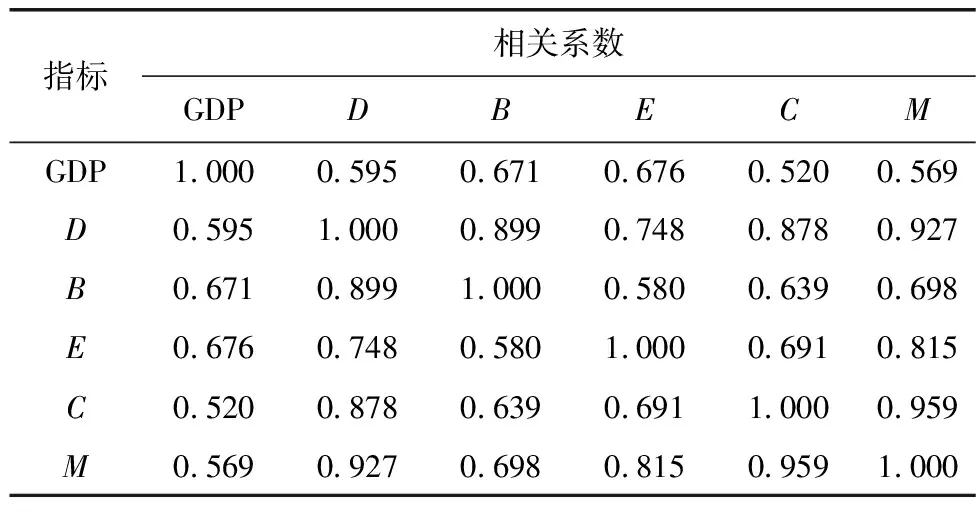
表2 各中心性与GDP指标Pearson相关性矩阵

2.3 网络韧性分析

采用中断情景建模中的随机攻击策略与基于中心性指标的蓄意攻击策略[15],根据多种中心性排序策略分别对单条连边封闭、多条连边封闭、单个节点封闭、多个节点封闭4种情景进行仿真模拟,对网络整体韧性进行分析。

2.3.1 单条连边封闭分析

分析高速网络中每条连边的重要性,若连边因突发事件进行了管控或交通封闭时,依次计算道路失效后最大加权连通子图比例以及加权网络连通效率 (图 7)。

单条连边失效后,全省高速公路网客、货运连通性能够保持较高值,最大连通子图规模以及网络连通效率保持在初始状态的85%以上。其中,当(东莞市—宝安区)之间的通道遭到封闭时,网络受影响最大,高速公路网客、货运最大连通子图规模分别下降9.63%和9.93%;高速公路网客、货运连通效率分别下降11.51%和11.58%。由此表明,东莞市与宝安区之间的高速通道在全省高速路网客货运周转中起到较大的作用,其次,S、E下降幅度较大其他通道有龙岗—宝安、南海—白云、番禺—荔湾、白云—花都等,下降幅度达到5%。

2.3.2 基于连边中心性多条连边封闭分析

为分析多条通道封闭后对全省高速公路连通性的影响,基于不同连边中心性序列采取蓄意攻击,对连边逐个进行封闭,观察网络连通性指标的变化,结果如图8,其中B′e为非加权介数中心性。

由图 8能够看出,道路在随机失效策略情况下,网络连通性指标下降速率最慢;B′e序列蓄意攻击下的下降速率稍高于随机失效序列,在Be序列的蓄意攻击下,网络连通性指标下降速率远高于B′e序列,验证了加权中心性指标识别重要道路的有效性。进一步分析,随机失效序列中前10%通道封闭后,客、货运最大连通子图规模分别下降8.72%与9.29%,网络全局连通效率分别下降11.65%与12.6%,此时网络具备一定稳健性;当Be序列中的前10%通道封闭后,客、货运最大连通子图规模下降幅度分别达到65.98%与56.92%,网络全局连通效率下降幅度分别达到68.27%与60.68%。图9为客、货车流量Be排名前10位连边被封闭后的网络连通性指标累积下降幅度。

图9充分说明,核心节点之间的高速通道被封闭将会严重影响整个高速路网的客、货运连通性。

2.3.3 单个节点封闭分析

当对节点进行封闭管控时,与其相连的高速道路将无法通过该点,该区县节点在全省高速路网中的连通作用暂时失效,这将会降低网络中各节点之间的通行效率,分析结果见图 10。

东莞市、宝安区、白云区封闭对高速路网的连通性影响最大,网络最大连通子图比例与全局连通效率平均下降幅度为20.47%和22.95%,其中东莞市封闭后全路网货运连通效率下降幅度达到31.58%,其次是龙岗区、番禺区、南海区、天河区、顺德区、中山市等,上述两个客货运连通性指标平均下降幅度在8%～10%之间。

2.3.4 基于节点中心性多个节点封闭分析

以货车流量加权为例,使用5种不同节点中心性指标D、B、C、E、M,逐一封闭节点后网络连通性变化情况如图11、图12。

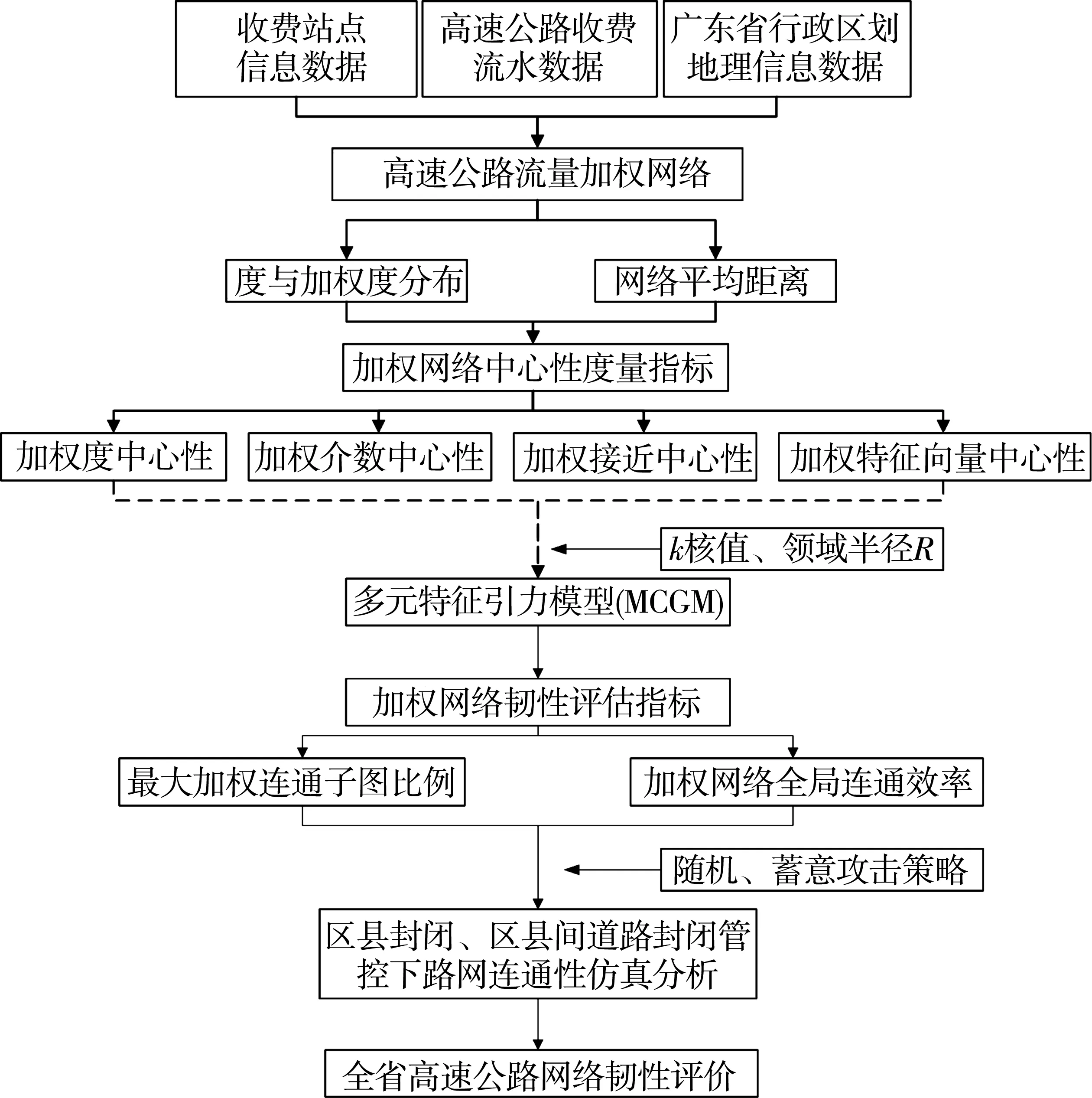
图1 研究技术路线Fig. 1 Research technical route

图2 邻域半径及邻域节点Fig. 2 Neighborhood radius and neighborhood nodes

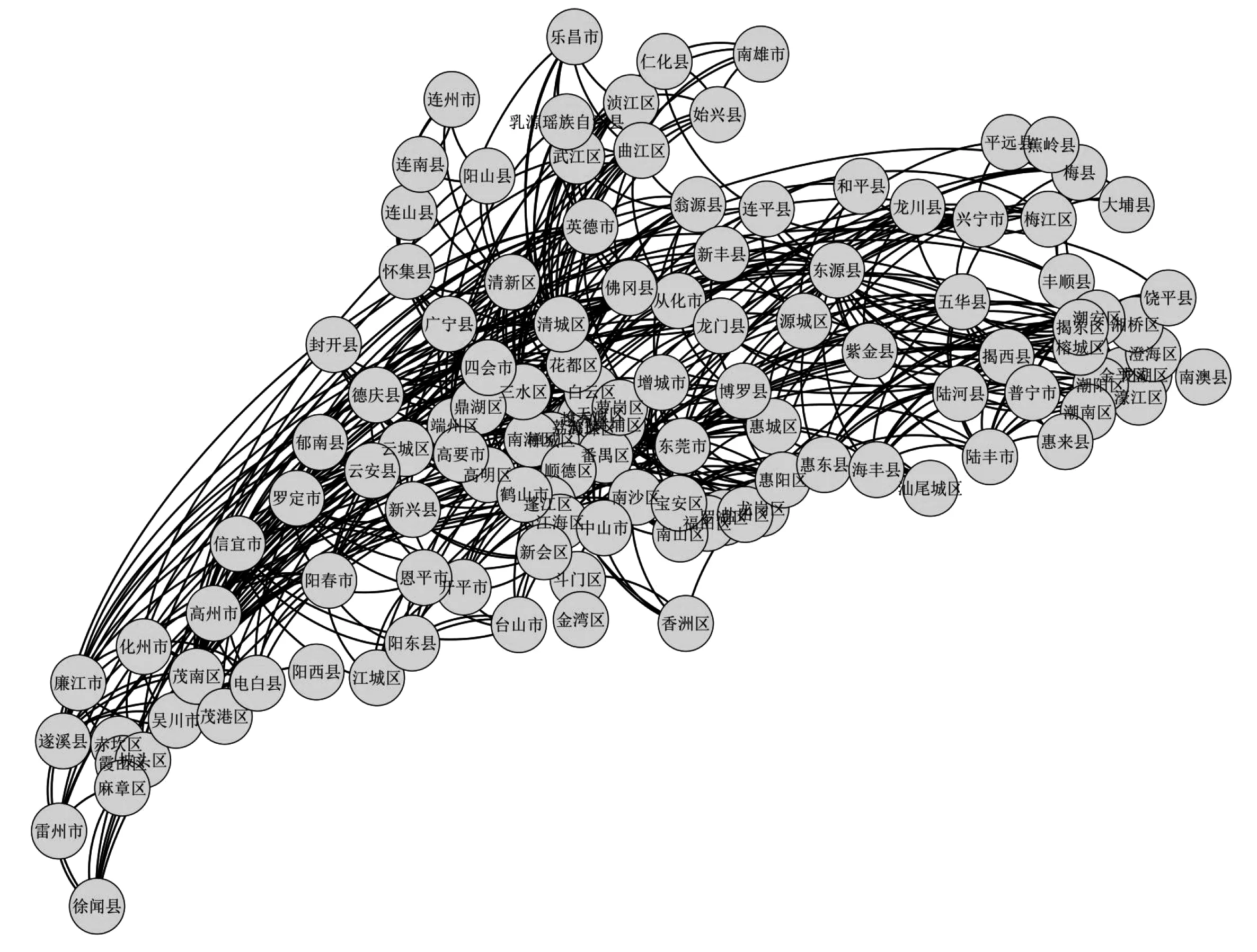
图3 广东省高速公路网络结构Fig. 3 Structure of highway network in Guangdong Province

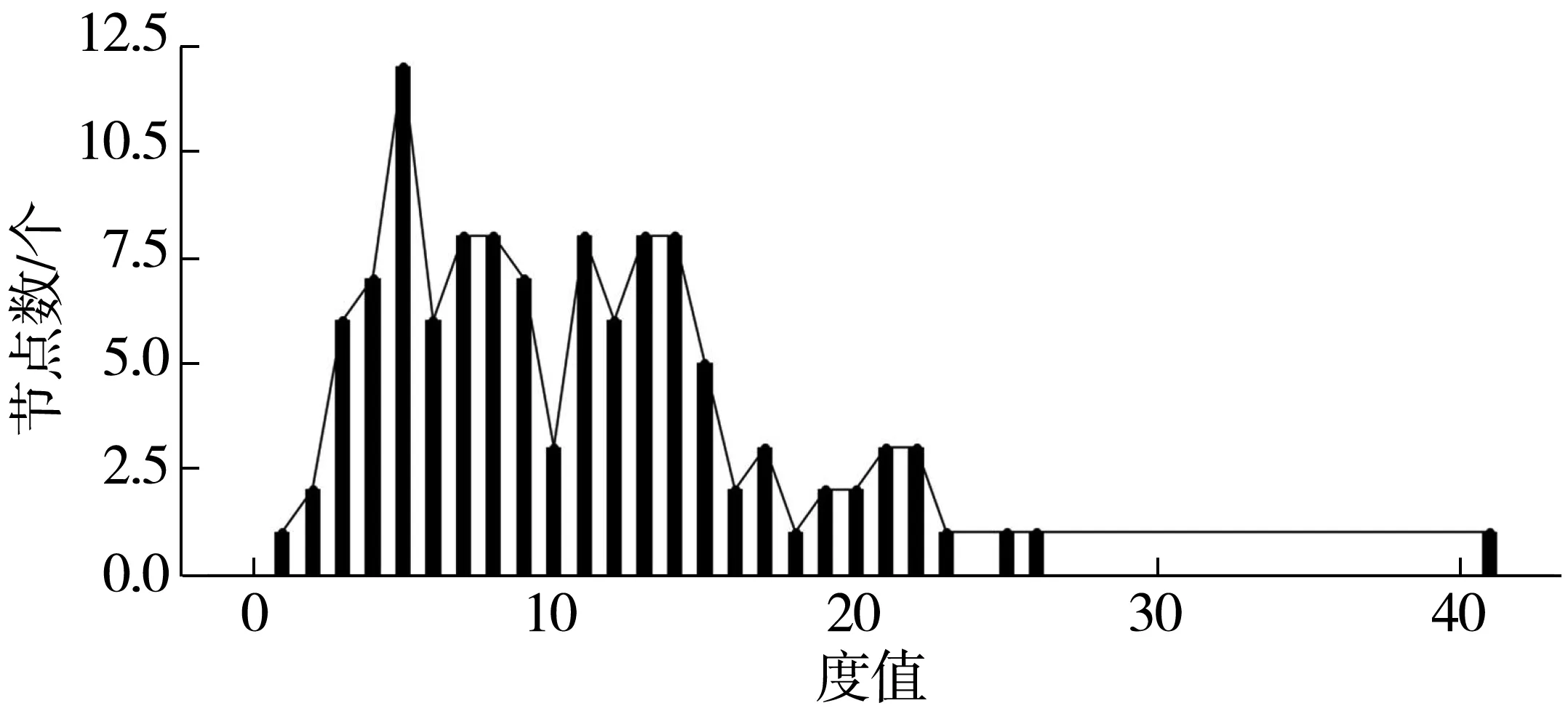
图4 网络度分布曲线Fig. 4 Network degree distribution curve

图5 高速公路流量加权网络加权度分布Fig. 5 Weighted degree distribution of highway flow weighted network

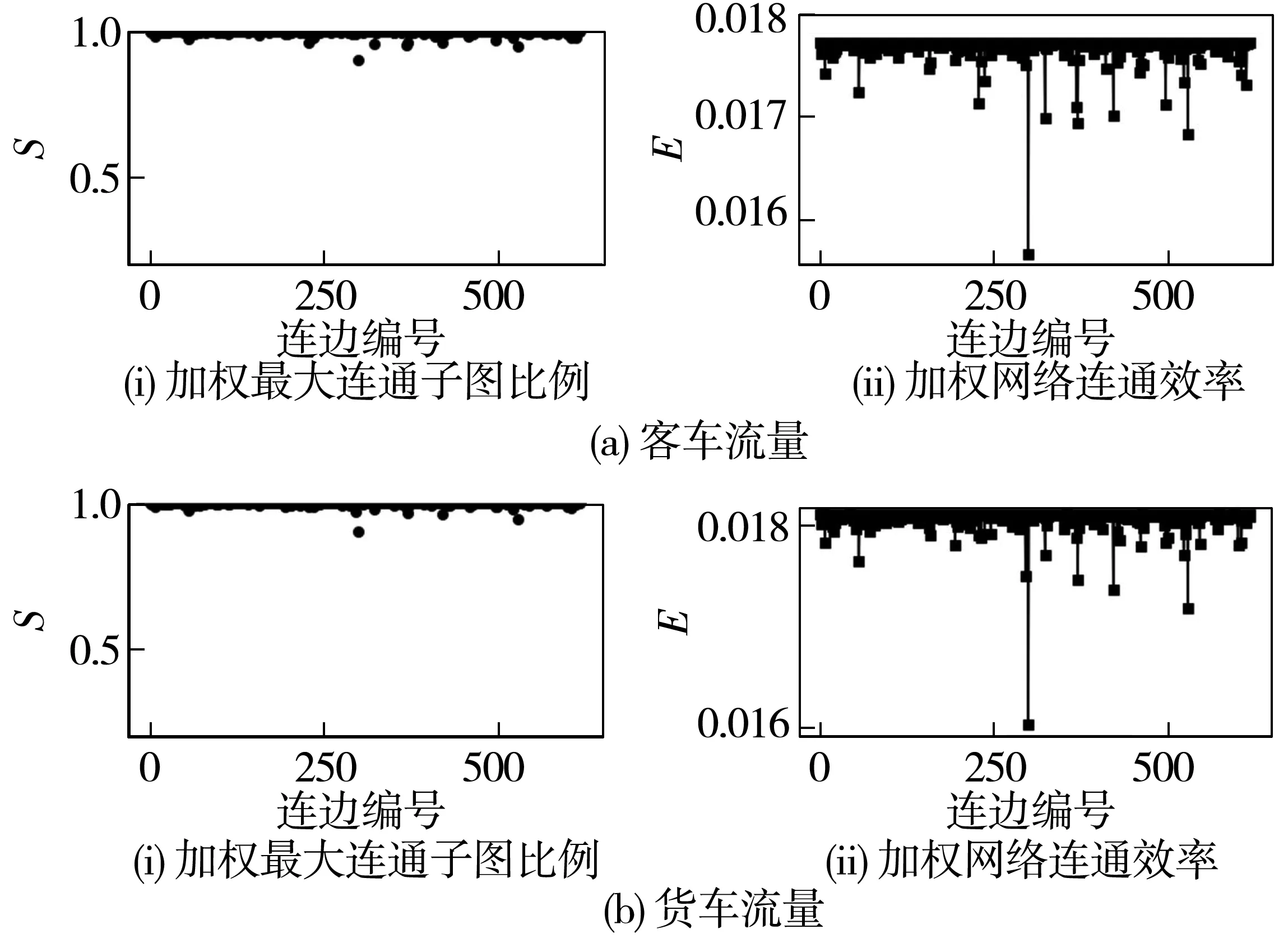
图7 单条连边封闭网络韧性分析Fig. 7 Resilience analysis of single edge closed network

图8 多条连边封闭网络韧性分析Fig. 8 Resilience analysis of multiple edge closed network

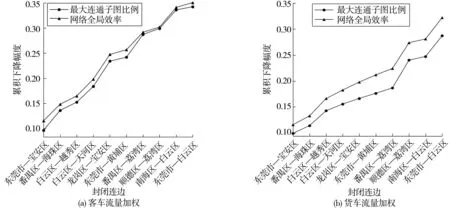
图9 多条连边封闭后网络韧性指标累积下降幅度Fig. 9 Cumulative decrease percentage of network resilience index after multiple road closures

图10 单个节点封闭网络韧性分析Fig. 10 Resilience analysis of single nod closed network

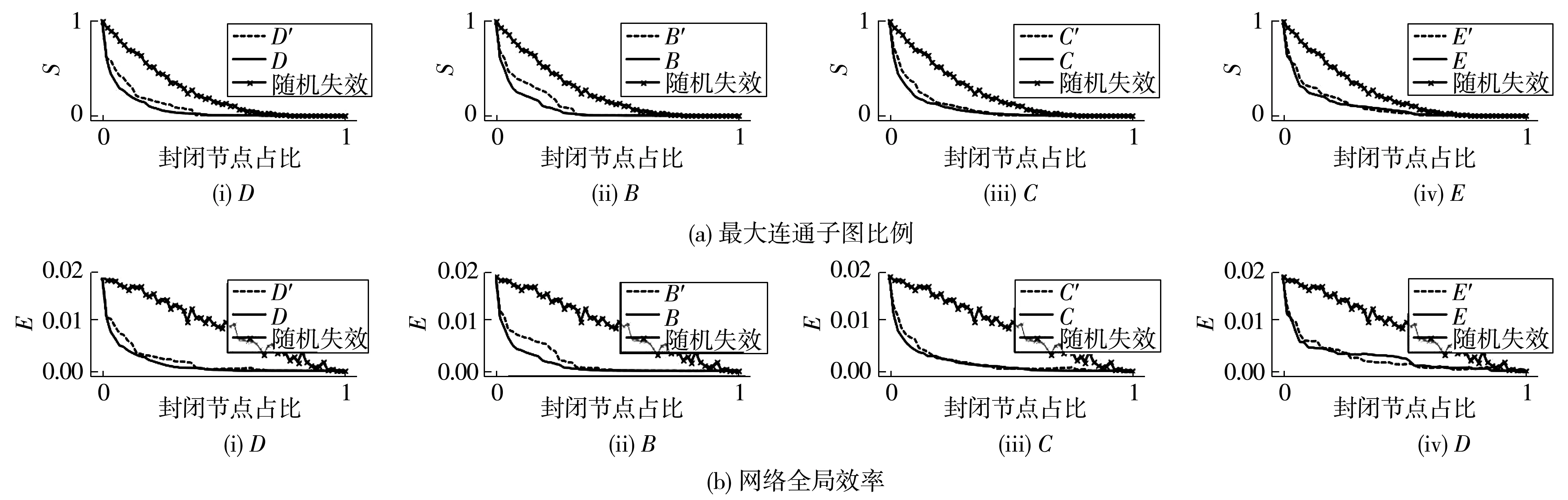
图11 货车流量加权下多个节点封闭网络韧性分析Fig. 11 Resilience analysis of closed networks in multiple nodes under weighted freight traffic flow

图12 多指标对比分析Fig. 12 Comparative analysis of multiple indexes

图11(a)为节点封闭后最大连通子图比例的变化情况,图11 (b)为节点封闭后网络全局效率的变化情况。对于前4个中心性指标,加权中心性指标(D′、B′、C′、E′)曲线均位于非加权中心性指标曲线与随机失效曲线下方,网络连通性能下降速率更快。由此进一步表明,加权中心性指标能够更好识别出路网中的关键节点。当各加权中心性序列前10个节点失效后,路网最大连通图比例平均下降73.68%,全局效率平均下降74.35%。由图12可知,当M中前20%节点封闭后,全网连通性指标平均下降幅度达92.52%,整个高速路网系统面临瘫痪风险,客、货车运输活动将难以开展,表明当高速路网中多个重要性较高的节点进行封闭管控后,整个高速路网的客货车运输活动受到严重影响。

由图12可知,E曲线整体下降速率较低,其次为C。而M曲线整体下降速率较快,位于大部分曲线下方,在5个中心性指标曲线中形成一条“包络曲线”。对比其他4个中心性指标,M序列前20%节点封闭后,网络连通性指标平均下降幅度最大,网络最大连通子图比例与全局效率相对损失分别达93.31%和91.74%。由此充分说明,集成了节点的多种特征包括节点位置、邻居数量以及邻居影响等信息的M模型能更好地识别出高速路网中的关键节点,参照表 1中M的节点序列,可知白云区、东莞市、宝安区、南海区、番禺区、顺德区、花都区、罗湖区、中山市、天河区等区域是全省高速路网中的核心区县节点。

对M指标中的邻域半径R进行灵敏度分析,如图13。以货车流量加权为例,通过计算得到该网络节点间最大连边数为5,计算领域半径取值R=1～5时,多个节点封闭下网络连通性变化情况。随着邻域半径R的增大,从R=3开始下降曲线重合,而在前20%节点序列中,R=2时平均下降速率最大,识别效果最优。可以推测,当邻域半径R取值过小时,对邻域节点的影响度考虑不足,未能准确识别核心节点;而当邻域半径R取值过大时,由于网络的高度连通性,会造成部分边缘节点中心值偏高,识别准确度下降。

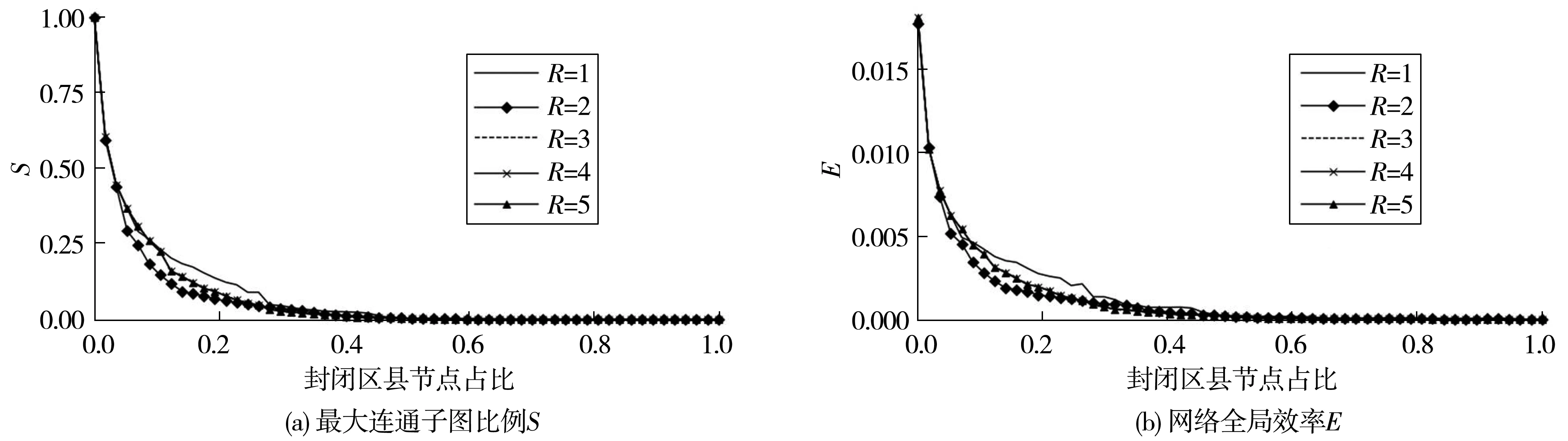
图13 多元特征引力模型邻域半径R灵敏度分析Fig. 13 Sensitivity analysis of neighborhood radius of multi-characteristics gravity model

3 结 论

基于P空间映射方法,融合高速公路网客、货车通行流量,笔者建立了高速公路加权网络模型,并对传统中心性指标及韧性评估指标进行改进,并对广东省高速路网韧性进行仿真分析,研究结果表明:

1)广东省高速公路网络中97.39%的节点客车流量加权度低于20万辆/d,95.65%节点货车流量加权度低于3万辆/d。以大湾区为核心的“十字型”高速路网联系廊道较为明显,处于广东省核心位置的粤港澳大湾区城市群的节点加权度较高,体现出较强的交通集聚效应。

2)相比于传统中心性指标,基于客、货车流量的加权中心性指标以及多元特征引力模型的中心性指标能更准确识别出真实高速路网中核心节点与重要连边通道。同时在高速公路网络前20%核心节点识别中,综合考虑节点特性的M指标更具优势。不同邻域半径R对识别效果会产生影响:当邻域半径R取值过小时,对邻域节点的影响度考虑不足,未能准确识别核心节点;而当邻域半径R取值过大时,由于网络的高度连通性,会造成部分边缘节点中心值偏高,识别准确度下降。

3)粤港澳大湾区中的东莞市、宝安区、白云区、顺德区、中山市、天河区等为高速通道核心区域,其中东莞市、宝安区、白云区封闭后网络最大连通子图比例与全局连通效率平均下降幅度为20.47%和22.95%。以上述区域为代表的前20%区域进行交通封闭管控后,全省高速公路加权网络的网络最大连通子图比例与全局效率累积损失分别达到93.31%和91.74%。

4)研究结果为量化高速公路网韧性特征提供了思路,后续研究可进一步考虑区域管控下高速路网流量的重分配与响应策略,对时空交通动态韧性进行更深入分析。