双丁坝流场及回流特性数值研究
范晓飚,曾 倩,冀 楠,钱志鹏,邓小兵
(重庆交通大学 航运与船舶工程学院,重庆 400074)
0 引 言
丁坝作为河道中经常可看见的河道整治建筑物,研究其周围水流特性具有重要的水力学研究价值。同时,这项研究对于确定丁坝的坝长以及合理安排丁坝间距等具有重要的指导意义。由丁坝束窄作用和坝间垂直漩涡的产生造成的水位凹陷、因高速水流泄入引起的不封闭回流区、坝间及坝后漩涡个数、回流区长度和宽度、坝间底面剪切应力的大小均为影响丁坝护岸的重要因素。
国内外众多学者对丁坝附近的水流特性问题进行了较为丰富的研究,但对双丁坝坝间、坝后的流场及回流特性的研究鲜有报道。M.PANDEY等[1]通过对角度为90°的弯道T形丁坝进行冲刷试验得出,随着长度以及弗劳德数的增加,丁坝的冲刷量也随之增加,当丁坝翼长加长时,丁坝冲刷随之减少;宁健[2]采用数值模拟与水槽试验相结合的方法进行研究,研究河宽缩窄率以及弗劳德数对单丁坝绕流流场和丁坝间距对丁坝群的水流结构的影响;常福田等[3]在矩形水槽中对非淹没式丁坝群坝后沿程水流速度及回流变化进行了分析,提出了群坝间距的最合理布置规律;胡华峰[4]研究了单丁坝在水槽的绕流情况,并得出流速在坝后主流区要高于坝后回流区的结论;郑艳等[5]研究了回流区长度因丁坝长度变化的影响,二维数值模拟研究了丁坝(非淹没型)的流场;J.YAZDI等[6]使用Fluent数值模型对具有自由表面流动的单丁坝周围流态进行了模拟,同时给出了床面剪应力分布,并分析了流量、丁坝长度和角度对床面剪应力分布的影响;R.KUHNLE等[7]使用声学多普勒测速仪在一个有淹没丁坝的固定冲刷床上的密布网格上测量了三维流速,得出了一般的速度分布以及近场流动结构;李洪[8]通过数值模型对单丁坝和双丁坝在淹没和非淹没条件下丁坝影响区域内流场变化规律及自由水面的影响趋势进行研究,并采用二维和三维数学模型研究丁坝周围流场及水面模拟方法,根据实际的河道整治工程,选取合适的数学模型;徐晓东[9]研究表明,非淹没正交双体丁坝不同坝长使得河流在丁坝坝体附近的水流绕流形态及坝后水面和流场变化变得复杂,当水流流经上游丁坝时,随着坝长的增加,最高壅水面提高,主流区回落幅度增大,主流宽度缩窄增强,过流流速持续增大,同时1号丁坝回流区对2号丁坝的影响程度越来越强;韩玉芳[10]研究表明,水流流向丁坝上游产生壅水现象使得水面向丁坝另一侧河岸倾斜,而在丁坝断面后水面普遍下凹,坝头因水流过分密集,会出现局部冲刷坑。
笔者采用计算流体力学软件STAR-CCM+,以RANS方程为基础,结合VOF方法和Realizable湍流模型,对双丁坝流场及回流特性进行了数值模拟;同时,通过与实验数据对比,验证了所采用数值模拟方法的可靠性;利用该数值模型探究了丁坝长度(河宽缩窄率)以及坝距对航道水位、流速变化、回流区影响和航道底面剪切力的变化。
1 数值方法
笔者采用了不可压缩流动的RANS方程,其中控制方程包括连续性方程和动量方程,分别如式(1)、式(2):
(1)
(2)
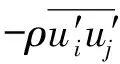
同时,对于式(1)、式(2),采用Realizable湍流模型进行封闭。在此模型中,湍流动能k和湍流耗散率ε的方程分别如式(3)、式(4):
(3)
(4)
式中:k为湍流动能;ε为湍流耗散率;μt为湍流黏性系数。
另外,笔者特别关注了自由液面的影响。自由液面的处理采用VOF界面捕捉法。其基本原理在于通过分析网格单元中流体和网格体积的比例函数来确定自由液面,以追踪流体的变化,而不是跟踪自由液面上质点的运动。
笔者采用Realizablek-ε湍流模型的考虑有两个:一是笔者课题组在前期研究船舶流态时,对此湍流模型进行了相关研究,确认此湍流模型在船舶尾部三维区域内的流态模拟仍能获得较好的计算精度[11],但仍然要说明的是,船舶尾部的型线光顺程度要远好于丁坝矩形坝头,使得计算结果变差[12],但k-ε的计算精度能满足船舶精细化研究,而对于丁坝这种外形简单的水工建筑,其精度是可以保证的;二是文中研究侧重点在宏观流场变化,而且将数值结果与试验结果进行对比,确认在距丁坝一定距离外的河道流态与试验结果吻合度较好,因此即使丁坝附近的流态不符合现实情况,也认为其并不影响较大范围内的河道流态变化。
2 丁坝回流区分区
丁坝分为4个区域,如图1。Ⅰ区位于丁坝上游,称为壅水区;Ⅱ区为主流区;Ⅲ区为AC线以内的区域,其中,A点为丁坝坝头,C点为水流流向分叉点,水流在C点分成流向下游和反向流向上游,BC线以内即为负流速区,BC线以外即为正流速区;Ⅳ区为恢复区,水流恢复到无丁坝状态。
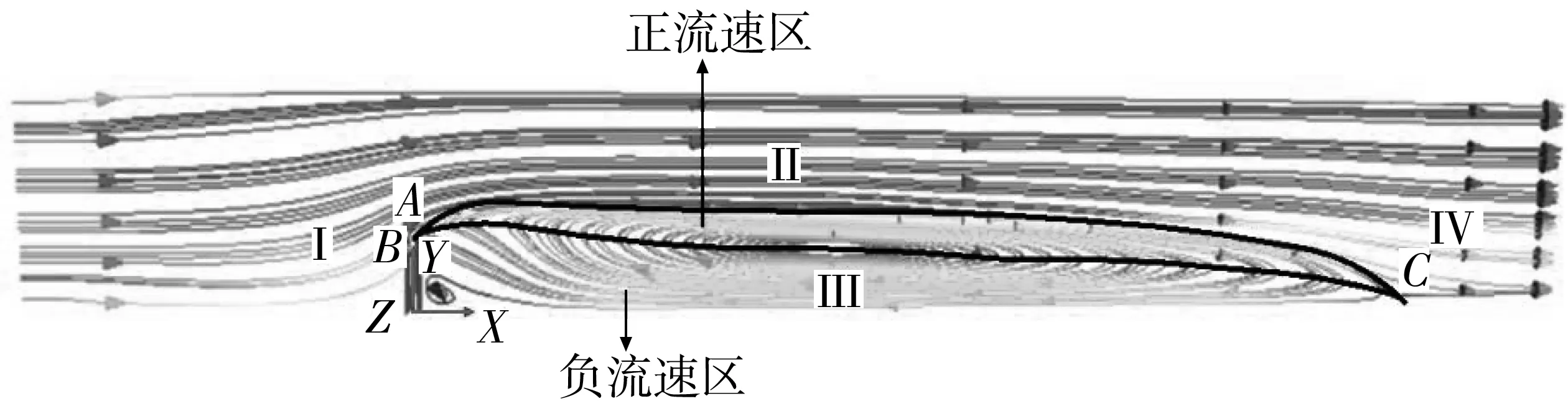
图1 丁坝附近水流分区Fig. 1 Water flow zoning near spur dike
3 数值验证
3.1 丁坝流场模拟
丁坝流场的验证参照J.JEON等[13]的试验。
水槽模型的尺寸为6.5 m(长)× 0.9 m(宽)× 0.262 5 m(高),初始水深为h=0.210 0 m。丁坝厚度D=0.040 0 m,高度H=0.262 5 m,轴线长l=0.300 0 m,此模型为非淹没式直丁坝。水流进口位于丁坝轴线前1.500 0 m处,进口处水流速度为U0=0.144 0 m/s,且进口水流量保持恒定,Q=0.027 0 m3/s。模型的进口和顶部被设定为速度进口,出口设定为压力出口,其他边界设定为无滑移壁面。丁坝计算模型的边界条件及坐标系示意如图2(a)。

图2 网格及探针线布置示意Fig. 2 Grid and probe line layout diagram
3.2 网格无关性验证
首先进行了网格无关性验证,采用了3种不同密度的网格对计算区域进行测试。这3种网格分别为粗糙网格s1、中等网格s2和精细网格s3。网格数量分别为488 84、111 656和259 548,以验证网格密度对结果的影响。
在丁坝上、下游选取4个河道截面,并设置4根探针线来测量水流流速,通过将所测结果与试验结果进行对比来验证流场模拟的准确性。4根探针分别位于X/L=-3.33,-0.90,1.67,3.33处,探测范围覆盖整个河道宽度。丁坝模型一半水深平面探针线的布置如图2(b)。
中等网格和精细网格的模拟结果更贴近于实验数据(图3)。考虑到计算工况计算域很大,部分丁坝算例为了研究丁坝后回流区特性而极大地延长了计算域的横向长度。因此在综合考虑计算精度和计算时间两个因素的前提下,选择了中等网格s2。

图3 4根探针下3套网格X向流速模拟值与实验值比较Fig. 3 Comparison between simulated and experimental values of X-direction flow velocity for three sets of grids under four probes
4 计算结果及分析
4.1 计算工况
丁坝坝长l和坝距d是双丁坝影响河道流态的主要因素。文中计算工况中设定航道总长L=135 m,航道宽度为B=17 m,河道左侧入口流速恒定为U0=0.9 m/s,计算工况的初始水深为h=2 m,如图4。分别改变丁坝坝长l和坝距d,从而获得不同的河道流态,所有工况设置如表1,共计算10组不同坝长和坝距下的计算工况。入口流速是依据模拟工况中坝长为1.7 m丁坝的速度傅汝德数与长江航道平均流速中常见丁坝的速度傅汝德数相等的原则换算而来。河宽缩窄率为丁坝坝长和河道宽度的比值。
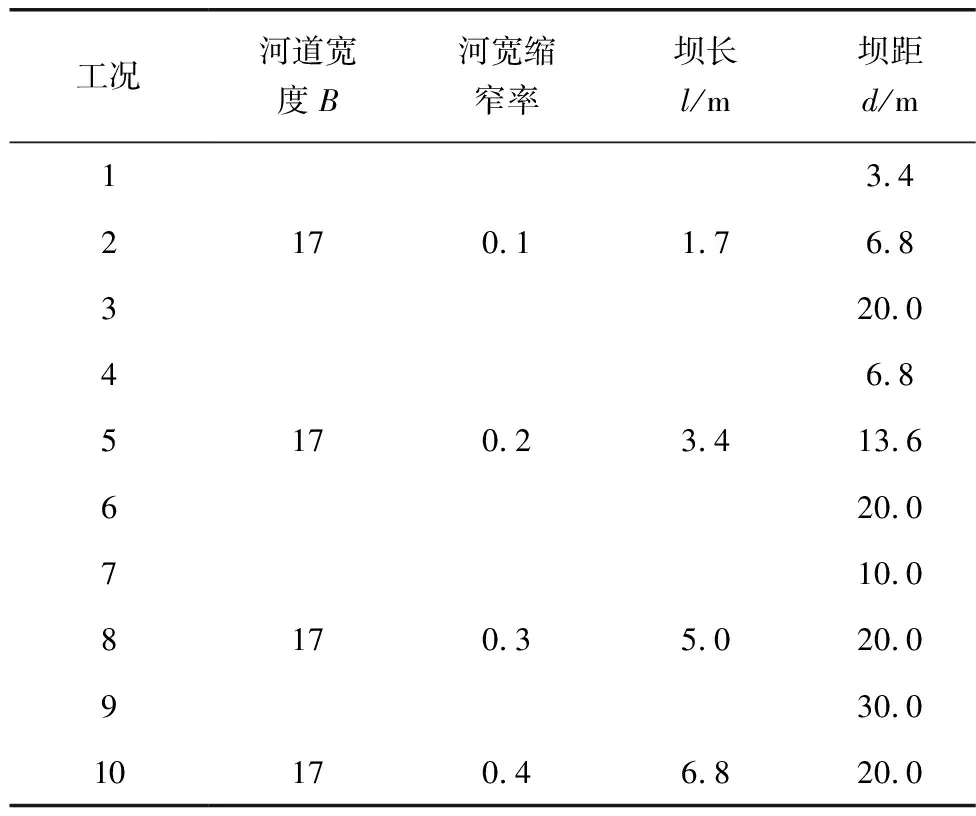
表1 计算工况

图4 计算工况俯视图Fig. 4 Top view of calculation condition
数值计算稳定的判别为高流速区漩涡分裂及融合。图5展示了河宽缩窄率为0.4时坝后高流速带和低流速带在一个周期内的摆动情况。由图5可以发现,在一个周期内,上部高流速带内形成了多个高流速核心漩涡,随后这些漩涡逐渐融合。而在低流速带内,漩涡核心首先融合成一个单一漩涡,与高流速核心区上下对应,随后又分裂为多个漩涡,形成了明显的周期性变化,即数值计算稳定。
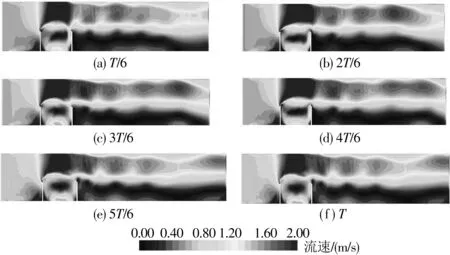
图5 河宽缩窄率为0.4时流速分布周期性摆动示意Fig. 5 Flow velocity distribution periodic oscillation diagram when river width narrowing rate is 0.4
4.2 航道水位变化
4.2.1 坝距一定时,丁坝长度(河宽缩窄率)对水位的影响
当水流流向丁坝时,受丁坝阻力作用,水流流速降低,水位壅高;当水流流到丁坝位置时,由于河面束窄,水力坡度变化,梯度增大;当水流绕过丁坝后,由于水流惯性作用,主流持续收缩,水位降低明显,然后水流持续扩散与天然河流相连,恢复到无丁坝的平稳情况。为了研究当坝距一定时,丁坝长度(河宽缩窄率)对水位的影响,以丁坝坝距d=20 m为例,分析不同丁坝长度(河宽缩窄率)时的河道水面水位高度云图(图6)。其中,为了更明显看出波面起伏情况,将波面高度扩大5倍,丁坝高度为原高度,如图6(e)。由图6可知,随着丁坝长度(河宽缩窄率)的增大,丁坝上游的壅水高度及壅水范围逐渐增加,两丁坝之间的水面跌落也越明显,形成水面凹陷,且凹陷范围覆盖整个河道宽度。产生这种现象的原因有两种:

图6 不同河宽缩窄率时河道水面水位高度云图Fig. 6 Cloud map of river surface water level height with different river width narrowing rates
1)当左侧入口水流在流至上游丁坝位置处,由于丁坝的束流作用,河道收窄,使流过此处的水流流速增大且水位提高;流过上游丁坝后又由于河道宽度重新变大而流速减小,水位降低,形成明显的水位跌落现象,从而产生水位凹陷Ⅰ。
2)由于水流绕过上游丁坝坝头一定角度后边界层产生分离,分离点以下位置沿坝头表面逆向流动,并在两坝之间形成旋转角速度较大的立轴漩涡,从而造成水位凹陷Ⅱ。
4.2.2 丁坝长度(河宽缩窄率)一定时,坝距对水位的影响
两种坝长下不同坝距的自由液面处水位分布如图7。由图7可以看出,因丁坝的壅水作用,上游丁坝坝前水位升高。随着坝距的增大,下游丁坝后方水位的凹陷区域逐渐减小,水位逐渐升高。当坝距增大到4倍坝长时,水位的凹陷区域从丁坝下游收缩至两丁坝之间。由图7(d)可知,下游丁坝坝头处形成了一个低水位凹陷区,并向丁坝下游逐渐脱落形成多个凹陷区域,产生振荡现象。同时水面形成的波浪向下游传播,当丁坝坝长较长时,双丁坝会造成坝后水流流态不稳定。

图7 不同坝距的水位分布Fig. 7 Water level distribution at different dam distances
4.3 航道流速变化
4.3.1 坝距一定时,丁坝长度(河宽缩窄率)对流速的影响
当水流遇到上游丁坝时,上游来流速度比较稳定,在水流通过丁坝时,会产生明显的水流偏转,形成主流区和回流区。主流区内的流速迅速增加,一旦水流越过丁坝,主流区的流速持续上升,并在坝后形成低速回流区。笔者分析了不同河宽缩窄率下流场流速的变化。不同河宽缩窄率下的流速分布如图8。由图8可以看出,下游丁坝位于上游丁坝的回流保护范围内,随着河宽缩窄率的增加,挑流作用增强,主流区收缩断面减小,流速明显增大。坝间回流区流速逐渐增大,对两坝间航道冲刷加剧;下游丁坝后回流区随着河宽缩窄率的增加,流速逐渐增加,回流结束后,断面流速并没有马上恢复无坝状态,在有丁坝一侧还存在较长距离的小流速区,河宽缩窄率越大,丁坝一侧河岸受到的保护范围越大。其中绕流状态时双丁坝的布置既可以充分起到束水、护岸作用,又可以保护第2个丁坝,缓解其坝头冲刷,在护岸范围比较大、通航级别和束水要求比较高的整治工程中可酌情推广使用。

图8 不同河宽缩窄率下的流速分布Fig. 8 Flow velocity distribution with different narrowing rates of river width
因为双丁坝的流场复杂,而且各流区的流速沿程变化较大,为了更直观观察坝长(河宽缩窄率)对流速的影响,对丁坝坝长为5 m,坝距为20 m的计算工况,在两坝之间x/L=0.26,探测范围为整个河道宽度处布置一条沿y轴方向的探测线,探测线位于水面处的不同河宽缩窄率流速变化如图9。由图9可知,水流流速随着河岸宽度的增加而增加,当河岸宽度增加到一定时,流速趋于平稳,直至水流趋近于航道无丁坝一岸时流速明显下降。
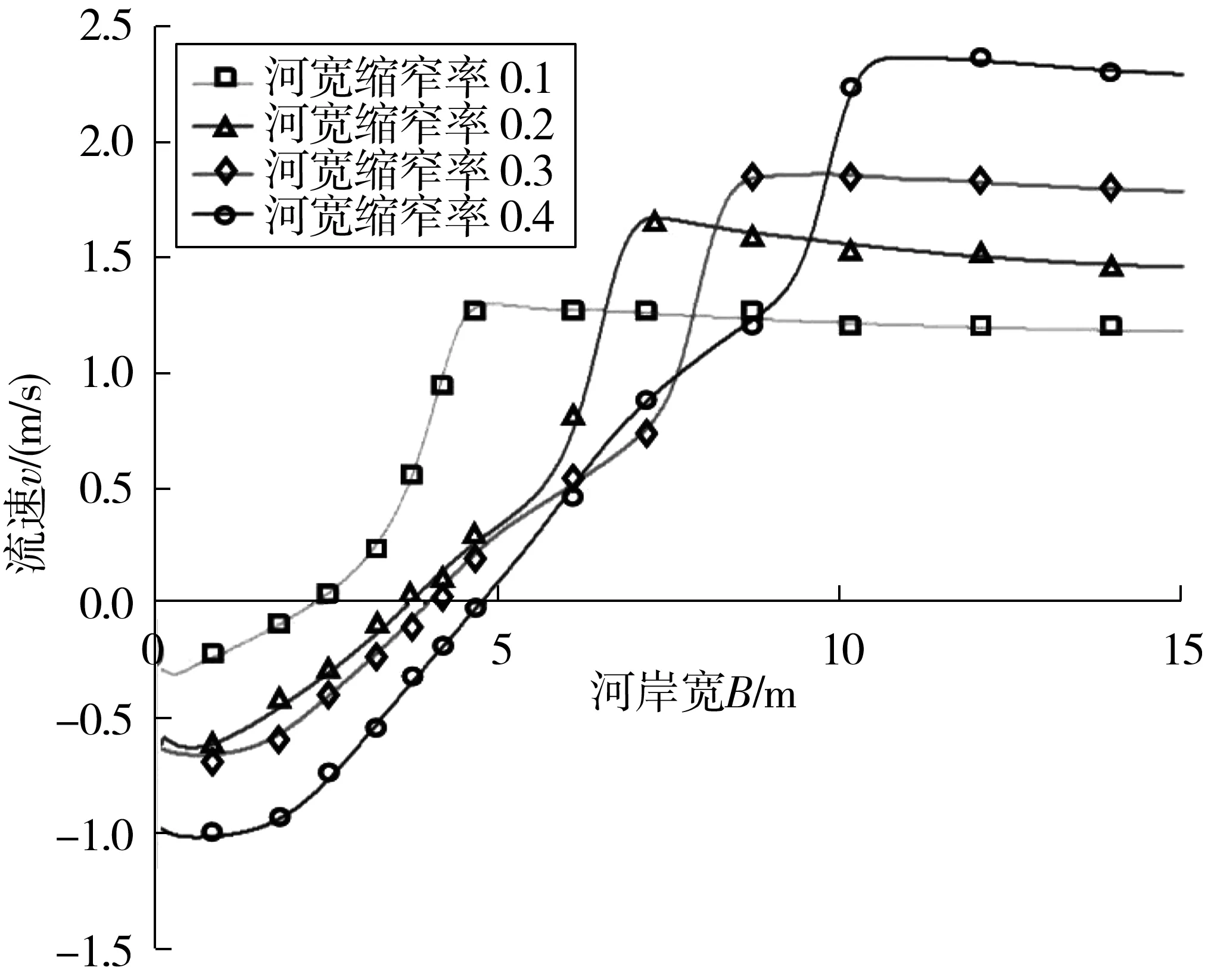
图9 水面处不同河宽缩窄率下的流速变化曲线Fig. 9 Flow velocity variation curves of different river width narrowing rates at water surface
4.3.2 丁坝长度(河宽缩窄率)一定时,坝距对流速的影响
不同坝距的流速分布如图10。由图10可知,随着坝距逐渐增大,两坝之间产生一个高流速漩涡且漩涡区域逐渐增大。两丁坝之间回流区不封闭,下游丁坝坝头处有高速水流泄入,从而削弱了双丁坝两坝之间的护岸作用。下游丁坝坝后高流速漩涡区随着坝距的增加而缩小,直至坝距增加到一定程度时,下游丁坝坝后流速趋于0,从而增强了双丁坝坝后的护岸作用。

图10 不同坝距的流速分布Fig. 10 Flow velocity distribution at different dam distances
4.4 航道回流区变化
4.4.1 坝距一定时,丁坝长度(河宽缩窄率)对回流区的影响
不同河宽缩窄率的流线分布如图11。坝后回流区的长度定义为图1中A、C两点间在X方向上的纵向距离;回流区宽度定义为图1中BC曲线上在Y方向上的最大横向距离。由于丁坝的束窄作用,主流区水流突然急速收缩,流速增大,水流冲击上游丁坝迎水面后,在坝间出现回流,时均流线分为两种情况:第1种水流保持前进运动继续向下游丁坝发展;第2种为坝后水流与侧壁分离,形成极度紊乱的回流区并形成一个顺时针的漩涡。水流绕过下游丁坝坝头后,仍会形成一段收缩断面,回流区形成一系列顺时针漩涡,直至回流消失,水流恢复到无丁坝状态。

图11 不同河宽缩窄率的流线分布Fig. 11 Streamline distribution of different river width narrowing rates
为了方便比较,将参数无量纲化,不同河宽缩窄率的回流区变化情况如表2。由表2可知,当坝距一定时,随着河宽缩窄率的增加,坝间回流长度与坝长的比值及回流宽度与坝长的比值随之减小,下游丁坝坝后漩涡个数也随着河宽缩窄率的增加而增加,同时坝后回流长度与坝长的比值及回流宽度与坝长的比值随之增大,回流区的漩涡范围逐渐增大。

表2 不同河宽缩窄率的回流区变化情况
4.4.2 丁坝长度(河宽缩窄率)一定时,坝距对回流区的影响
不同坝距回流区变化情况如表3。由表3可知,当坝长一定时,随着坝距的增大,坝间回流长度与坝长的比值及回流宽度与坝长的比值随之增大。同时坝后回流长度与坝长的比值及回流宽度与坝长的比值随之减小,回流区的漩涡范围也逐渐减小。不同坝距对回流区影响如图12。由图图12(c)、图12(e)可知,水流流过上游丁坝后在坝间形成一个顺时针漩涡,水流再绕过下游丁坝坝头,在坝后形成回流区,直至恢复到无丁坝时水流。而图12(a)和图12(d)情况有些许差异,水流流过上游丁坝后在两坝间坝头位置处形成一个顺时针漩涡,水流继续流过下游丁坝,在坝后形成回流区。当水流回流到下游回流区尾部时,水流反向流回下游丁坝并流入两坝之间,形成一个逆时针漩涡。

图12 不同坝距对回流区影响Fig. 12 Influence of different dam distances on reflux area
4.5 航道底面剪切力变化
4.5.1 坝距一定时,丁坝长度(河宽缩窄率)对剪切力的影响
不同河宽缩窄率对底面剪切力的影响如图13。由图13可看出,随着坝长(河宽缩窄率)的增大,上游丁坝坝头处因丁坝束窄作用所受到的剪切应力值逐渐增大且受力范围逐渐扩大,两坝之间的低剪切应力漩涡范围也随之减小,下游丁坝坝前处出现一条高剪切应力冲刷带,并随着坝长(河宽缩窄率)的增加,冲刷带逐渐加宽,剪切应力逐渐增大,下游丁坝坝后形成的高剪切应力漩涡中心值也逐渐增大。

图13 不同河宽缩窄率对底面剪切力的影响Fig. 13 Influence of different river width narrowing rate on bottom shear force
4.5.2 丁坝长度(河宽缩窄率)一定时,坝距对剪切力的影响
坝长为3.4 m时不同坝距的底面剪切应力分布如图14。由图14可知,当坝长一定时,坝距越长,两坝之间的底面剪切应力增大,这说明双丁坝坝距过大的情况下,水流对坝间距的河道冲刷强度大,造成丁坝护岸效果被削弱。同时下游丁坝后方剪切应力亦呈现脱落涡的形式,并随着坝距的增大,剪切应力脱落涡逐渐明显且数值增大。剪切应力的大小是由于水流变化引起的,由于高速漩涡的移动,造成不同位置处水流流速变化,因此剪切应力的大小也随之变化。

图14 坝长为3.4 m时不同坝距的底面剪切应力分布Fig. 14 Distribution of bottom shear stress at different dam distances when the dam is 3.4 m long
5 总 结
笔者通过CFD数值计算的方法,对双丁坝河道内水流流态进行了数值模拟,得出了不同丁坝长度(河宽缩窄率)以及坝距对航道水位变化、流速变化、回流区影响和航道底面剪切力等参数变化的详细数据,得到以下结论:
1)航道水位变化:当坝距一定时,随着河宽缩窄率的增大,丁坝上游的壅水及范围增加,两坝间的水面跌落也越明显,形成两种水面凹陷,且凹陷范围覆盖整个河道宽度。当坝长一定时,随着坝距的增大,下游丁坝后方水位的凹陷区域减小,水位升高,水位的凹陷区域从丁坝下游收缩至两丁坝之间。
2)航道流速变化:随着河宽缩窄率的增加,挑流作用增强,主流收缩断面减小,流速明显增大。坝间回流区流速增大,对两坝间航道冲刷加剧。随着坝距逐渐增大,坝间回流区不封闭,有高速水流泄入,下游丁坝坝后高流速漩涡区减小,直至流速减小为0。
3)航道回流区变化:随着河宽缩窄率的增加,坝间回流长度及宽度与坝长的比值减小,下游丁坝坝后漩涡个数增加,坝后回流长度及宽度与坝长的比值增大。随着坝距的增大,两坝间回流漩涡长度及宽度与坝长的比值增大,坝后回流漩涡长度及宽度与坝长的比值减小。当坝长l=5.0 m,坝距d=10.0 m及坝长l=3.4 m,坝距d=6.8 m时会发生水流逆流回两坝间,形成逆时针漩涡。
4)航道底面剪切力变化:随着河宽缩窄率的增大,上游丁坝坝头处的剪切应力值增大且受力范围扩大,下游丁坝显现高剪切应力冲刷带,冲刷带加宽,冲刷加剧。随着坝距增大,坝间底面剪切应力增大,下游丁坝后方剪切应力脱落涡明显且数值增大。

