不同重力环境和倾斜角度对毛细管内界面振荡行为的影响*

霍晓智 王 晴 顾君苹 王战涛 于 强 王庆功

1(中国科学院国家空间科学中心 北京 100190)

2(中国科学院大学计算机科学与技术学院 北京 100049)

3(中国空间技术研究院 钱学森空间技术实验室 北京 100094)

4(中山职业技术学院 机电工程学院 中山 528400)

0 引言

毛细现象对人类生活及空间活动均有重要的意义。在微重力条件下，由于重力的缺失，毛细力占主导地位，由毛细力驱动的流体分布是空间热控、流体管理的关键基础[1-3]。毛细结构内的流体动力学行为受毛细尺度、流体物性、壁面润湿性、毛细管倾斜角度等因素的影响[4-7]，在重力变化时会诱导界面发生振荡现象，毛细结构内两相界面的运动过程较为复杂。

20世纪初，Lucas-Washburn方程（L-W方程）的提出从理论上建立了重力条件下毛细管内界面上升的规律，并证明了毛细界面上升前期高度h与时间t的关系（h2～t）。然而，L-W方程忽略了惯性对毛细动力学的影响。针对这一问题，Bosanquet[8]将液柱的动量变化加入L-W方程中，Szekely等[9]、Levine等[10]从进入毛细管口流体的能量入手修正方程，从而更加准确地描述了毛细管内界面运动演变规律。Quere[11]通过实验观察到毛细管内界面的振荡过程，Wang等[5]通过理论分析研究了毛细管内界面振荡机理。

随着研究的不断深入，对常规毛细现象已经有较清楚的认识。然而，在空间微重力环境下，毛细管内的界面爬升过程有所变化。随着重力的消失，界面振荡行为也随之消失。Dreyer等[12]、Stange等[13]在落塔中进行了微重力环境不同尺度的毛细实验，提出毛细界面运动可分为三个阶段：初始阶段以毛细力为驱动力，第二阶段以入口处流体流动引起的对流力为主导力，在第三阶段，管间摩擦力对毛细运动的影响较大。Wang 等[2]研究了微重力环境毛细管尺度对毛细驱动行为的影响，发现随着毛细管尺寸的增加，毛细界面运动进入最后一个阶段的时间也随之增加。此外，Xu等[14]、Chen等[15,16]研究了不同形状毛细管对毛细管内界面爬升动力学的影响。

在空间及地面应用中，毛细管并非一直处于与重力加速度垂直的方向。由于毛细管的倾斜或重力环境的变化，毛细管内的界面过程会受到进一步影响。Gao等[7]通过实验研究了倾斜角度对毛细管液柱上升高度的影响，所得实验结果与L-W方程存在明显差异。Tian等[17]和Barroso等[18]通过理论建模的方式研究了Taylor-Hauksbee Cell倾斜时的毛细上升问题，证明了高度与时间遵循h～t1/3的规律。

目前，对于非常重力环境和倾斜毛细管内的界面振荡现象理论分析仍不充分。为解析这一问题，本文建立了倾斜毛细管内界面变化过程的理论模型，分析了毛细界面振荡的动力学效应。同时针对毛细管建立数值计算模型，开展了模拟研究，获得了可视化结果。将理论分析、数值模拟结果和现有实验结果进行对比，证明了两类模型的可靠性，同时详细分析了不同重力环境和倾斜角度对毛细管界面上升及振荡行为的影响规律。

1 理论模型

1.1 倾斜毛细管内界面位置随时间的演化规律

如图1所示，毛细现象是液体依靠毛细力作用在毛细管内自动爬升的过程。依据能量平衡原理，毛细上升和/或下降的动态过程不仅与表面能）、动能）、重力势能）、净输入能）、黏性能的耗散（）有关，还与入口/出口处压力损失（） 的瞬态变化有关[5]。因此，能量守恒定律遵循以下公式：

图1 倾斜毛细管内弯液面位置与结构Fig.1 Schematic of meniscus when capillary tube is tilted

表面能的变化率为

其中，R，Δz，l的 表示如图1所示，σ为表面张力。

动能的变化率为

其中，ρ表示液体密度，v为速度。

重力势能的变化率为

其中，g为重力加速度，α为毛细管相对于垂直方向的倾斜角度。

质量变化率为˙，表达式如下：

流入毛细管中的净动能变化率为

流入毛细管中的净重力势能变化率为

由式(6)和式(7)可得毛细管中净输入能变化率为

根据Hagen-Poiseuille关系，黏性阻力产生的压降可表示为

其中，µ为液体的黏度，A为截面积；毛细管中产生的黏性阻力为

由黏性阻力产生的黏性耗散能量变化率可写为

根据流体力学理论，压头损失可以计算为

其中，ξ为液体运动的局部阻力系数，可通过液池（A1）和毛细管（A2）的横截面积之比估算（见图2）[5]，即

图2 压头损失计算Fig.2 Schematic diagram of head pressure loss

结合上述公式，液体上升/下降的能量平衡方程可写为

当毛细管倾斜角度α=0时，毛细管垂直于液面，式(15)与文献[5]一致。在一般情况中，液体对固体的润湿情况为部分润湿状态。因此，在计算该类问题时，需要考虑接触角的变化，即在式(15)的左边乘以接触角的余弦值（cosθ）。

1.2 动态接触角

液体与毛细管壁的接触角变化主要是由三相线处受力不平衡引起的，即

其中，θd表示液体与毛细管壁的动态接触角。

毛细力（Fc）为

其中，θ0为液体静止时与毛细管壁的接触角。

摩擦力（Ff）为

其中，ςf为接触线摩擦因数，cpin为钉扎力，可以用接触角滞后量化，u为接触线处的速度。

结合式(16)～(18)可得毛细过程中的动态接触角，即

则液体界面上升/下降的能量平衡方程如下：

1.3 Runge-Kutta求解微分方程

为求解上述微分方程，采用四阶Runge-Kutta法。具体求解过程如下。

由于式(20)为二阶非线性微分方程，因此需要先将方程转换为如下形式：

通过上式可将式(20)整理为

令如下等式成立：

则使用四阶Runge-Kutta迭代求解上述方程，有

其中，δ为迭代时间间隔（δ=10-3）。这里采用python实现四阶Runge-Kutta法，完成上述方程的求解。

2 数值模拟方法

2.1 物理场模型

为得到毛细界面的可视化演化过程，采用数值模拟方法研究了毛细管内界面的振荡运动过程。采用Comsol软件中层流两相流模型将流动物理场与相场耦合，假设毛细运动为不可压缩且互不混溶的牛顿流体，其动态模型使用Navier-Stokes方程。

质量守恒方程为

动量守恒方程为

其中，u，p，t分别表示速度场、流场中的压力和时间；界面处的密度ρ和黏度µ分别根据两相流体的体积分数加权计算得到，有

其中，Vf,1为流体1的体积分数，ρ1和ρ2分别为流体1和流体2的密度，µ1和µ2分别为流体1和流体2的黏度。

相场法是一种扩散界面方法，用于描述两相流界面的动态变化过程，可以通过求解相场方程直接捕捉运动界面。相场方程为

其中，ϕ，u，γ，λ，ψ分别为连续相场变量、流体速度、移动参数、能量混合密度、相场变量；ϵpf为控制界面厚度的参数。

移动参数γ为一个标量，定义为

其中，χ为迁移率，这里取χ=1m·s·kg-1。

混合能量密度λ有助于根据模型界面的表面张力调整界面厚度，定义为

相场变量ψ定义为

其中，ϕ=1为其中一相，ϕ=-1为另一相。

2.2 几何模型及计算方法

建立的二维毛细管几何模型如图3所示。其中下部储液罐为内径120 mm、高度45 mm的圆柱形容器，内部盛有高度为30 mm的液体。计算中采用三种不同的流体工质，具体参数见表1。数值模拟中采用的毛细管几何结构长度z= 100 mm，半径R=1 mm，其中一端浸入液体中（z0=10R），另一端与大气相连。图3中蓝色边界设置为润湿壁，将其设置为Navier滑移边界条件。

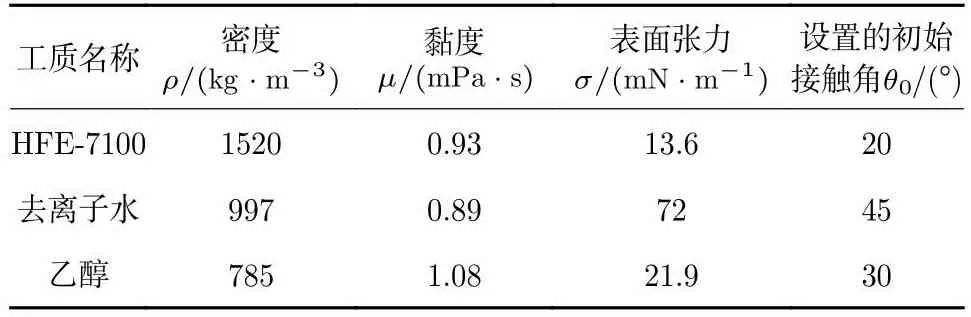
表1 流体参数属性Table 1 Properties of the fluid parameter

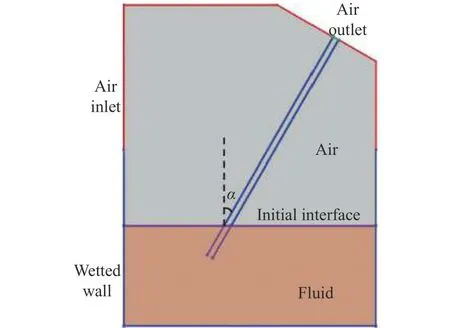
图3 倾斜毛细管几何模型Fig.3 Geometric model of tilted capillary tube in a liquid bath

3 结果与分析

3.1 模型验证

为验证上述理论模型及数值模拟结果的正确性，首先将常重力下垂直毛细管内的理论求解结果、数值模拟结果与文献[5]中的实验数据进行对比。工作流体使用HFE-7100，毛细管半径R=1mm，毛细管浸入液体的高度z0=6R，倾斜角度α=0，即毛细管垂直于液面放置，结果如图4所示。可以看出，重力环境会诱导毛细管内界面产生振荡，通过实验、理论模型和数值模拟得到的界面运动趋势基本相同。三种结果相比，实验获得的振荡过程阻尼最大，振荡衰弱过程最快，同时上下往复振荡的非对称性较为明显。这是由于实际物理过程中，毛细管内壁面的缺陷和非理想清洁状态均会影响动态润湿过程，并引起能量损耗。理论结果中由于考虑了毛细管端口液体吸入和流出的能量损失（见图2），较好地显示出界面振荡周期和非均匀振荡效应。数值模拟结果与实验出现一定偏差，这是由于模拟条件完全理想化，并且对入口处的局部能量损失考虑不足。整体而言，理论分析和数值模拟结果均能够复现由重力引起的毛细界面瞬态振荡过程，能够反映振荡幅值、峰谷位置、非对称性等特征。下文主要基于理论模型和数值模拟研究分析倾斜毛细管及不同重力环境下的界面振荡动力学行为。

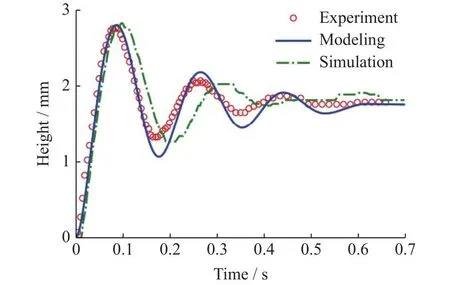
图4 垂直毛细管界面振荡过程的实验结果及理论分析与数值模拟结果对比Fig.4 Comparison of results of theoretical modeling,numerical simulation and experiment

3.2 不同重力水平对毛细管内界面运动的影响

为研究不同重力水平对毛细管内界面振荡行为的影响，将半径R=1mm的毛细管垂直液面放置（即α=0），浸入液面高度z0=10R，分别将重力水平设置为1g/6，3g/8，g和 2g。理论模型分析及数值模拟计算得到的瞬态界面过程如图5所示。可以看出，毛细管内界面的稳定高度随重力加速度的减小而增高。毛细管内的界面上升主要受毛细力驱动，当重力水平减小后，更多流体能够吸入毛细管内，界面达到新的高度后，流体重力与毛细力相平衡。同时，从曲线的瞬态发展过程可以看出，毛细管内界面的运动速度随重力作用的减小而增加，这是由于垂直方向上界面的受力不平衡增加了液柱上升的瞬时加速度。

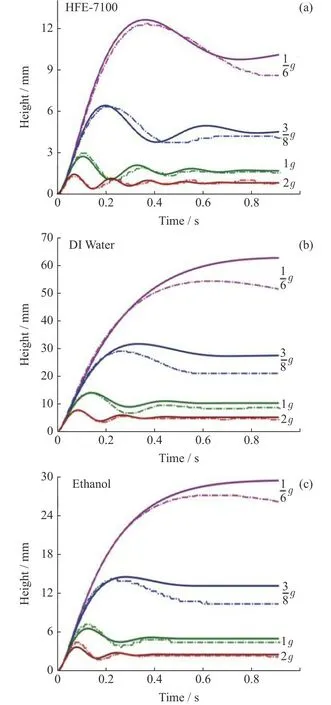
图5 不同重力下毛细管内界面的运动情况（实线为理论结果，虚线为数值模拟结果）Fig.5 Meniscus movement under different gravity levels (Solid line is for theoretical result while the dashed line is for simulation)

由图5还可以看出，毛细管内界面的振荡效应随重力水平的增大而增强。对于同一流体工质，Oh=µ/(ρRσ)1/2不变，而Bo=ρgR2/σ（其中g为重力加速度）随重力水平的增加而增大。当Oh≪Bo时，毛细现象受重力作用主导，毛细管内界面的运动从初始的惯性状态过渡到振荡状态[19]。因此，在相同条件下，重力作用越大，毛细管内界面振荡效应越显著。同时，毛细管内的界面振荡行为受工质物性的影响，为此定义了界面振荡率，即

其中，hmax为振荡的最大高度，hmin为振荡的最小高度，S为毛细界面最终的稳定高度。 通过本文分析可知，在常重力环境中，HFE-7100的振荡率为0.96，而去离子水与乙醇的振荡率相近，均为0.49。三种流体的振荡率与其对应的Oh/Bo关系一致，这表明毛细管内界面的振荡行为与Oh/Bo有关，随着Oh/Bo的增大，毛细振荡效应逐步弱化。

为进一步分析界面振荡过程中的能量耗散机制，针对工作流体HFE-7100，分析其在不同重力环境下主要的能量耗散随时间的演变过程，如图6所示。从图6可以看出，在毛细运动过程中由重力势能引发的耗散（）占主导地位（占总能量耗散的80%以上），几乎比其他能量耗散高1个数量级。所有的能量耗散均随着重力水平的减小而增加。这是由于能量耗散与毛细管内界面运动的速度直接相关。如前所述，重力水平越小导致界面运动速度越大，因此对应的能量耗散越大。

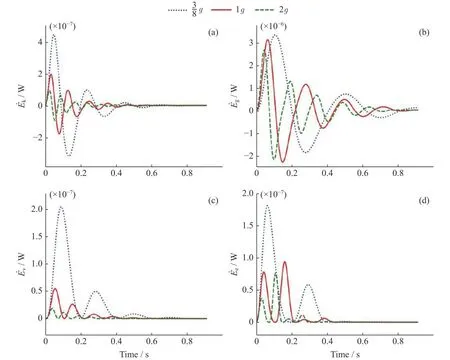
图6 HFE-7100在毛细管内界面运动的能量耗散过程Fig.6 Energy dissipation during capillary oscillation for HFE-7100

3.3 倾斜角度对弯液面运动的影响

进一步研究倾斜角度对毛细管内界面振荡行为的影响。在常重力环境下考虑毛细管相对垂直方向倾斜角度α为30°，45°，60°三种情况，结果如图7所示。从图7可以看出，无论倾斜角度如何，毛细管内界面最终稳定的垂直高度均相等。然而毛细管内界面的振荡行为与倾斜角度有较大关联，毛细振荡效应随倾斜角度的增加而逐步弱化。以HFE-7100为例，当毛细管倾斜角度为45°时，振荡率为1.21；当毛细管倾斜角度增加到60°时，振荡率增加到1.32。这是由于毛细管倾斜角度越小，沿毛细管方向的重力分量对毛细管内界面爬升的影响越大，振荡效应增强。由于物性差异，三种不同工质表现出不同的振荡特征。其中，HFE-7100密度较大、表面张力小，与重力效应相关的界面振荡较为显著，但界面平衡高度小；乙醇有较大的表面张力，因此对抗界面振荡的能力最强。

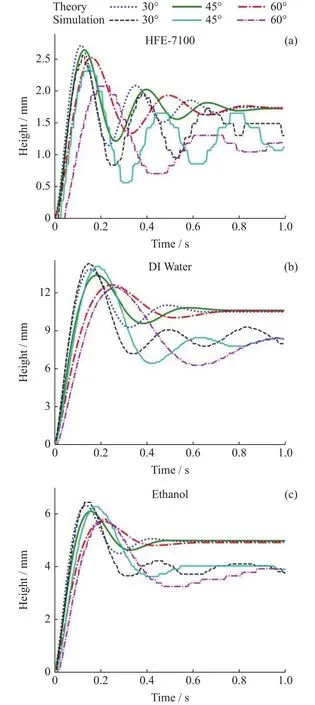
图7 不同倾斜角度下弯液面运动情况Fig.7 Meniscus movement under different tilt angles

图8为典型的界面振荡演化过程。此工况采用HFE-7100流体，毛细管倾斜角度分别为α=45°和α=60°。由图8可知，t=0.15s 时毛细管内界面处于向上爬升阶段，t=0.25s时毛细管内界面处于下降阶段，t=1s时毛细管内界面处于稳定阶段。从图8可见，无论处于哪个阶段，毛细管内界面均垂直于毛细管，但不完全对称，这与重力效应相关。同时，毛细管外也有显著的毛细效应，且右液面高度明显高于左液面，这与文献[20]研究的实心圆柱体倾斜浸入液面的现象一致。

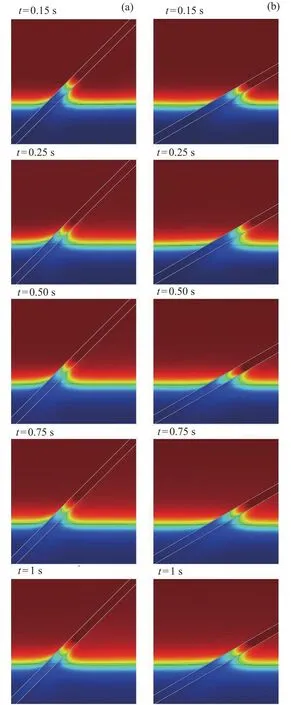
图8 HFE-7100在毛细管内运动的瞬态过程Fig.8 Meniscus movement of HFE-7100

4 结论

针对变重力及毛细管倾斜角度对毛细管内界面振荡行为的影响过程开展研究，建立了毛细管内界面瞬时上升高度的理论模型，并开展了数值模拟研究，通过与实验结果对比验证了理论模型和数值模拟的可靠性。研究结果表明：重力水平减小，毛细界面垂直方向上的不平衡力差变大，毛细管内界面稳定高度增高，运动速度增加，能量耗散增加；当重力增大时，毛细管内界面的振荡行为增强。同时，在毛细运动过程中由重力势能引发的耗散占主导地位，占总能量耗散80%以上。通过对比三种不同流体工质，发现HFE-7100由于密度最大，其振荡行为最显著，振荡率为0.96，而去离子水与乙醇的振荡率接近，约为0.49。当毛细管倾斜时，毛细管内界面的振荡行为由工质物性和沿毛细管方向的重力分量共同决定，随倾斜角度的增大而增强。