基于二维流场的方形断面钝体气动性能分析

王红艳，隽文烁

基于二维流场的方形断面钝体气动性能分析

王红艳，隽文烁

（齐齐哈尔大学 机电工程学院，黑龙江 齐齐哈尔 161006）

主要仿真分析基于二维流场的风致振动压电俘能器方形断面钝体的气动力，旨在探究方形断面钝体在不同攻角下的气动特性，为提高风致振动压电俘能器能量采集效率提供参考。首先通过与文献数据对比不同雷诺数下的斯托罗哈数，验证了有限元气动分析方法的正确性；然后分析二维流场中的方形断面钝体在0°～20°攻角下的横向气动力，通过多项式曲线拟合方法得到了气动力经验系数；随后通过对压电俘能器驰振控制方程进行数值求解，研究了风速对俘能器输出性能的影响。结果表明，在攻角为8°时，方形断面钝体的气动力性能最佳。在给定的参数条件下，压电俘能器的起振风速为2.6m/s，风速6m/s时，最大电压可达50.95V。

方形断面钝体；雷诺数；斯托罗哈数；气动力

当风遇到结构体表面时会引起流场的扰动，这些扰动不断扩大和衰减，最终形成周期性的涡旋，从而对结构产生气动荷载作用，表现为风致振动现象。风致振动包括涡激振动[1]、颤振[2]、驰振[3]和抖振[4]等。在驰振风能收集领域，俘能器的钝体结构设计至关重要，其形状和尺寸大小都是影响风致振动压电俘能器能量收集性能的重要影响因素。本文重点探究一种方形断面钝体在二维流场中气动力参数大小以及不同攻角下的气动力性能，为驰振压电俘能器钝体结构设计提供一定参考。

1 带方形钝体的压电俘能器

风致振动压电能量收集器是一种利用压电材料的压电效应将环境中的风能转化为电能的设备。它是一种绿色能源装置，不需要消耗任何化石燃料，也不会产生任何污染就可以实现能量的收集和储存。图1为风致振动压电俘能器的物理模型，俘能器由方形钝体、金属梁以及贴在金属梁夹持端根部的压电片组成。钝体截面边长为，高度为。钝体在来流风速的作用下发生垂直于来流的横向驰振，进而带动压电梁振动，基于压电效应将机械振动转化成电能输出。

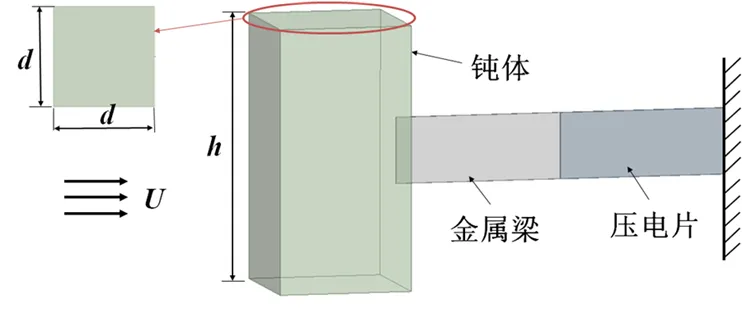
图1 风致振动压电俘能器的物理模型

2 理论方法

2.1 影响尾流脱落的主要参数

在流体力学中，雷诺数的大小可以用于判断流体在不同介质、不同流速下的运动状态是层流还是湍流。雷诺数的计算公式为

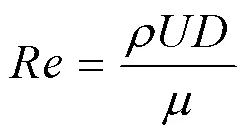
式中：为空气密度；为方形断面特征长度；为空气动力黏度。

斯托罗哈数是描述流体中振动现象的重要参数，通常用表示，它用来描述流体在非定常流动下的周期性涡脱规律。在雷诺数和钝体特征长度一定的情况下，漩涡脱落频率f与流体流速之间关系用公式表示为

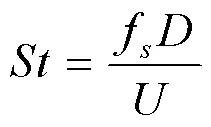
2.2 横向气动力计算

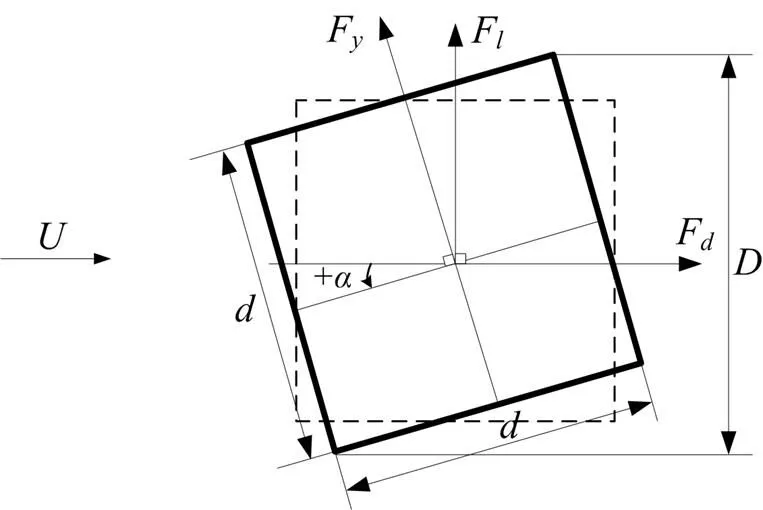
图2 方形截面钝体受力

只考虑二维流场时，每单位长度横向气动力F与来流风速之间的关系为[5]

对于对称结构，横向气动力系数C与升角之间的关系可近似写为[5]

3 二维流场仿真分析

3.1 仿真参数设置及流程

为探究方形钝体在二维流场中的气动力性能，首先需建立流场模型进行数值模拟计算。对于流体仿真而言，计算域的大小影响模拟计算的结果，计算域越大，流场壁面对计算结果的影响越小，计算结果越接近真实情况。特征长度为的结构置于流场中，上下壁面距离至少应为10，进出口距离至少应为20。本文分析钝体截面边长=40mm，由于攻角较小，对特征长度影响较小，可以认为==40mm。图3为流域环境模型。方柱居中放置，流场长度设为25，宽度设为12.5。网格划分采用结构化三角形网格。根据需要对钝体附近流场和后方尾流区域进行了加密处理，网格膨胀选用平滑过渡，过渡比为0.272，最大膨胀层数7层，增长率1.2。计算模型采用模型，近壁处理选择标准壁面函数，流场为空气场，密度为1.225kg/m3，粘度为1.7894×10-5Pa‧S。上下侧面设置为对称边界条件，无滑移壁面，壁面粗糙度常数设为0.5，入口来流速度设置为6m/s，湍流强度设置为5％，湍流粘度比设置为10，出口表压为0。瞬态计算需开启动网格，设置动网格边界条件，打开光顺和网格重构。采用Coupled算法处理速度-压力耦合问题，采用标准初始化从inlet开始计算。物理时间步长为0.001s，最大迭代步数设为20，至少应计算至充分绕流，使尾流漩涡脱落呈稳定的周期性变化为止。

图3 流场网格划分

3.2 结果与讨论

3.2.1 斯托罗哈数计算

为验证仿真模型的正确性，首先做了攻角为0度时的CFD数值模拟，将结果与文献[6-8]中的实验结果进行了比较。本文分析了8种雷诺数条件下方柱绕流的相关参数，雷诺数分别为1000, 3000, 5000, 10000, 13000, 16430, 18000, 20000，将不同雷诺数下计算的方形钝体的气动力特性通过快速傅里叶变换得到流场中的涡街脱落频率分别为1.0, 3.5, 6.0, 12.5, 15.9, 20.0, 22.0, 24.0Hz。图4为雷诺数=16430时的升力曲线和根据升力曲线得到的频谱。根据式(1)和式(2)可计算得到。与的关系如图5所示，数值模拟得到的值与文献数据（分别为1000, 3000, 5000, 13000）非常接近[6-7]，并且在较大（10000-20000）之间稳定在0.13左右[8]，说明本文使用的仿真分析方法是正确的。

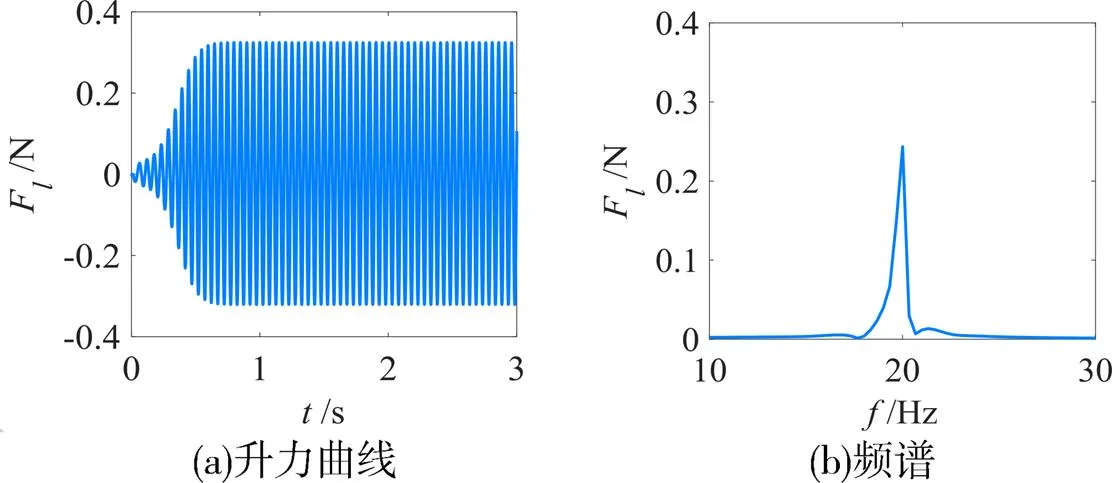
图4 升力曲线与功率谱（Re=16430）

图5 斯托罗哈数随雷诺数的变化情况

3.2.2 压力和速度云图

当钝体在空气中受到横向风升力的作用时，其尾流区域会形成周期性脱落旋涡。在一个脱落周期内，当涡流附着在结构上表面时，升力达到最大值。0°攻角对应的最大升力时的压力云图和速度云图如图6(a)(b)所示。当涡流附着在结构下表面时，升力达到最小值。0°攻角对应的最小升力时的压力云图和速度云图分别如图7(a)(b)所示。

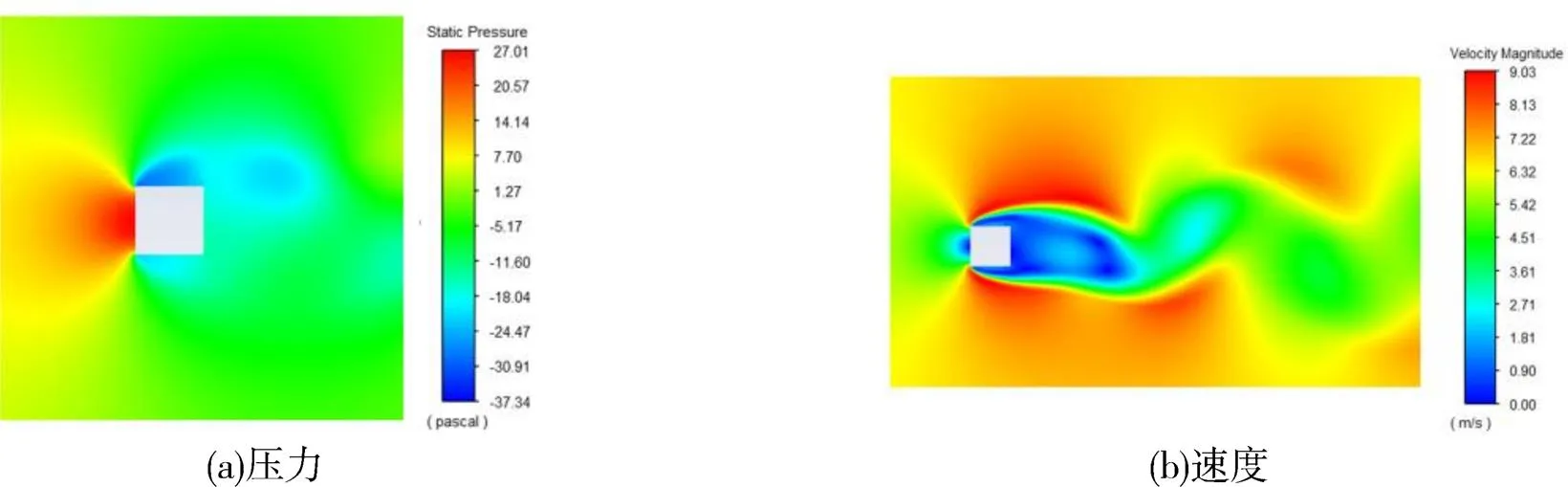
图6 压力云图和涡流场速度云图（最大升力）

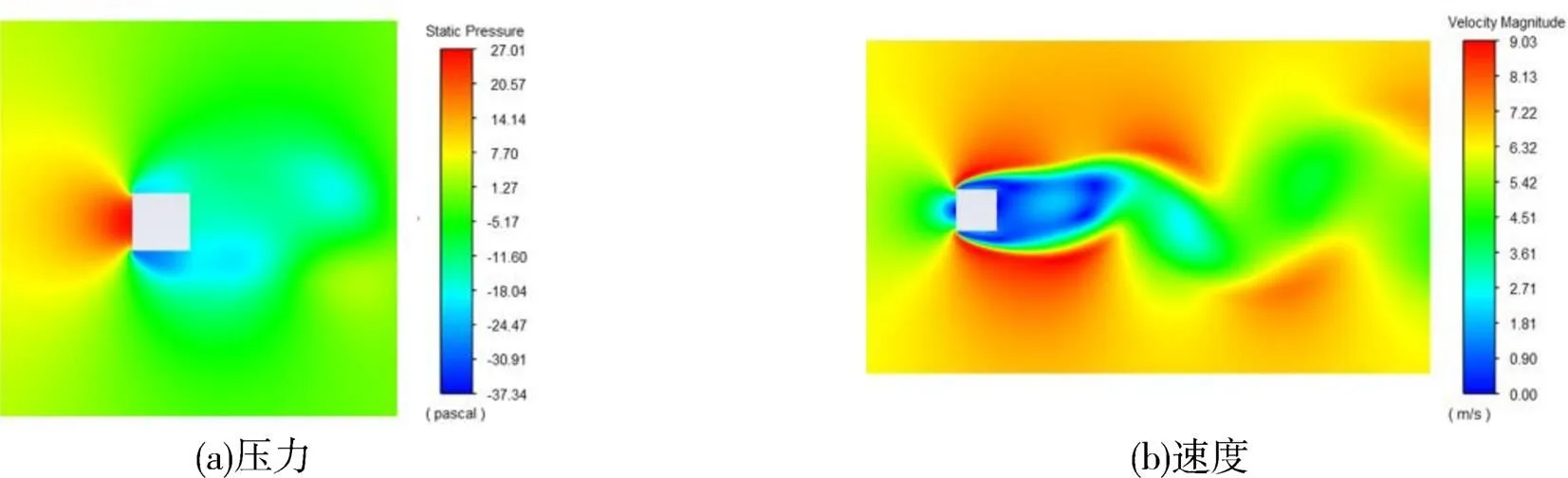
图7 压力云图和涡流场速度云图（最小升力）

由于环境风能的不可控性以及来流风方向的多变性，单一角度的气动力参数并不能充分评估阻流钝体的性能。为了更全面地了解方形钝体的横向气动力随不同风攻角的变化情况，本文在风速6 m/s下进行了二维数值模拟计算，在直角坐标系下，以轴为旋转中心，将钝体逆时针方向旋转，测量了攻角范围为0°～20°之间的升力F和阻力F，根据式(3)计算得到不同攻角下的横向气动力系数C如图8所示。由图8可知，当攻角为8°时方形钝体气动力系数最大，气动力性能更好。根据式(4)，忽略更高阶项，采用5次多项式拟合后得到气动力经验系数分别为1=3.72，3=-92.75，5=396.1。

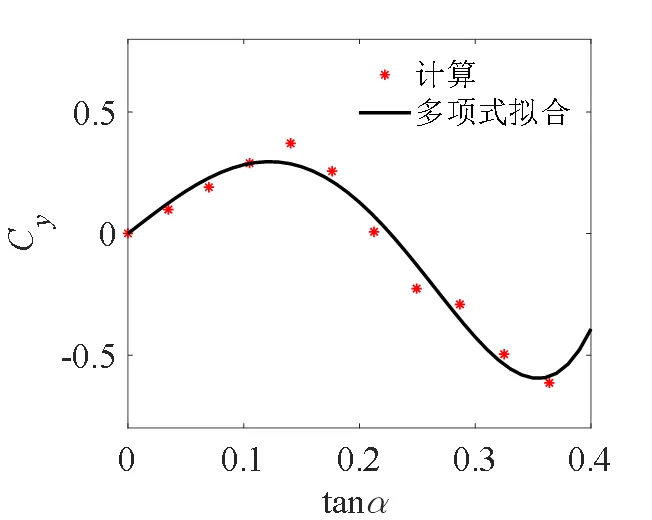
图8 不同攻角下横向气动力系数

4 带钝体结构压电梁输出性能分析

带钝体的压电梁可以简化成一个单自由度弹簧（）-质量（）-阻尼（）-压电系统，压电片外接负载电阻，如图9所示。在风激励作用下，压电俘能器运动位移为。

其单自由度集总参数模型为

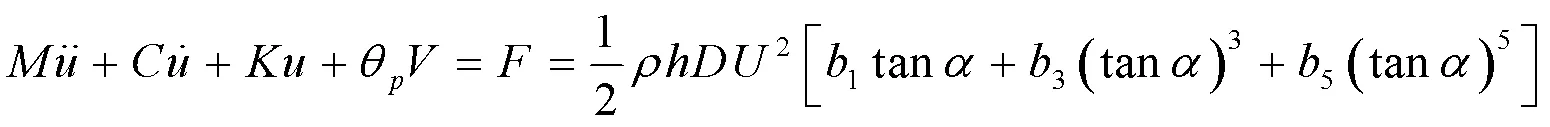
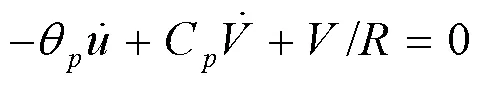
图9 单自由度系统

定义状态空间向量为

将驰振控制方程写成状态空间形式

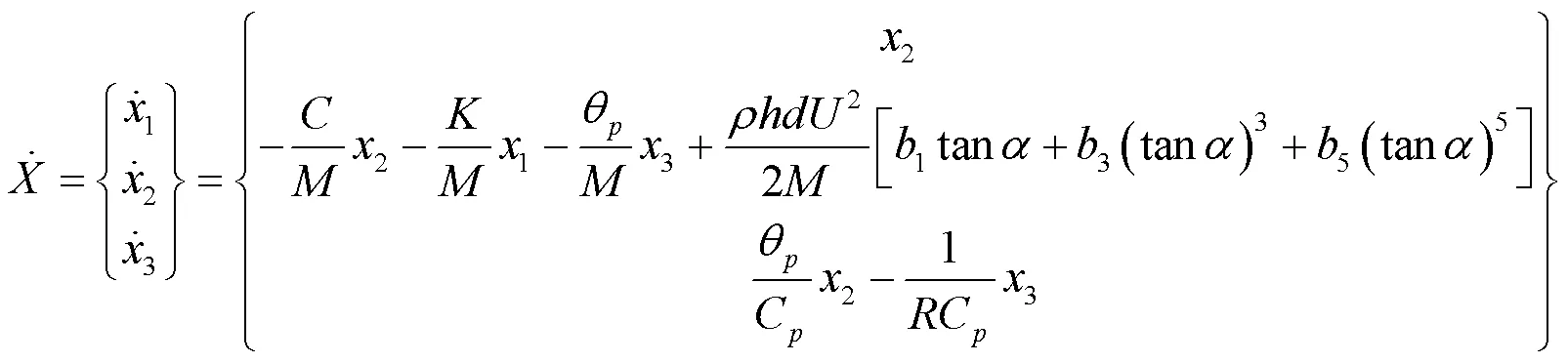
本文钝体高度=80mm，横断面边长=40mm。金属梁长=130mm，厚度为h=0.6mm。压电片长L=30mm，厚度为h=0.2mm。压电片和金属梁等宽，均为=10mm。金属梁材质为铝，压电片材质为PZT。计算得到压电梁等效质量为=0.009586kg，等效刚度=25.76 N‧s-1，机电耦合系数θ=9.93×10-5，压电片电容C=19.5nF。梁末端转角参数=11.54。定义阻尼=0.001，负载电阻=1MΩ，在MATLAB中使用ODE45对驰振控制方程进行数值求解。得到方形钝体俘能器在不同风速下的振幅和电压如图10所示。由图10可知，方形断面钝体俘能器的起振风速为2.6m/s。随风速增加，风致驰振压电能量收集器的横向位移和电压也在逐渐增大，在模拟条件风速为6 m/s时，最大振幅为13.7mm，最大电压为50.95V。

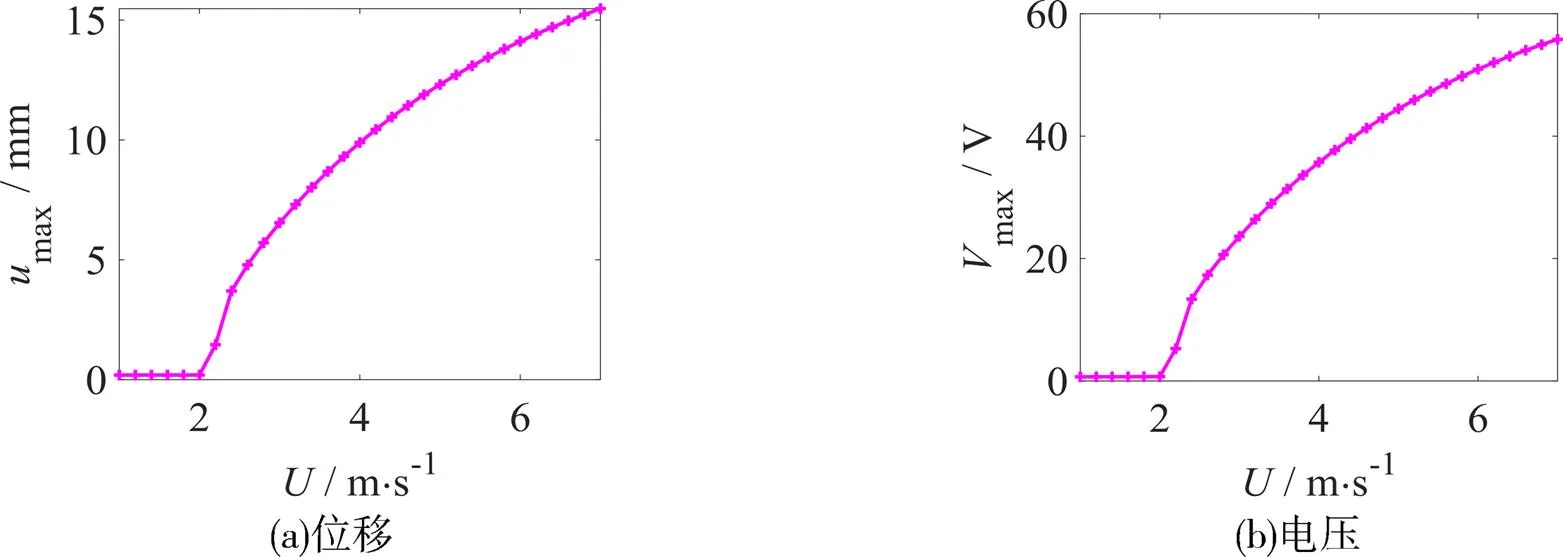
图10 振幅和电压随风速变化

5 结论

本文使用ANSYS Fluent软件对一种尺寸为40mm*40mm的方形断面钝体进行了气动力性能分析，结果显示，当其尾部涡流附着在结构体上表面时存在最大升力，附着在其下表面时具有最小升力。分析得到了不同攻角下方形钝体气动力系数，当攻角为8°时，方形钝体气动力系数最大，气动力性能更好，多项式曲线拟合得到气动力经验系数为1=3.72，3=-92.75，5=396.1。使用MATLAB ODE45计算压电俘能器驰振控制方程数值解，得到其起振风速为2.6 m/s，风速6m/s时最大振幅为13.7mm，最大电压为50.95V。

[1] 杜小振，MBANGO-NGOMA P A，常恒，等. 流致涡激振动压电发电风能采集技术模拟研究[J]. 振动与冲击，2022, 41(23): 168-174, 200.

[2] 刘祖军，贾明晓，杨詠昕. 箱梁表面的压力分布对颤振稳定性的影响[J]. 工程力学，2022, 39(12): 98-107, 129.

[3] 刘丽兰，吴子英，谭红波. 三稳态尾流驰振能量捕获系统发电性能研究[J]. 应用力学学报，2022, 39(03): 498-505, 526.

[4] 孙杰，黄庭轩，孙禄君，等. 基于压电纤维复合材料的抖振主动控制研究[J]. 机械强度，2020, 42(04): 770-776.

[5] WANG J, TANG L, ZHAO L, et al. Efficiency investigation on energy harvesting from airflows in HVAC system based on galloping of isosceles triangle sectioned bluff bodies[J]. Energy, 2019, 172: 1066-1078.

[6] LIU F, ZHANG W, PENG Z, et al. Fork-shaped bluff body for enhancing the performance of galloping-based wind energy harvester[J]. Energy, 2019, 183: 92-105.

[7] NORBERG C. Flow around rectangular cylinders: pressure forces and wake frequencies[J]. Journal of Wind Engineering and Industrial Aerodynamics, 1993, 49: 187-196.

[8] OKAJIMA A. Strouhal numbers of rectangular cylinders[J]. Journal of Fluid Mechanics, 2006, 123: 379-398.

Analysis of aerodynamic performance of bluff body with square-section based on two-dimensional flow field

WANG Hong-yan，JUAN Wen-shuo

(School of Mechanical and Electronic Engineering, Qiqihar University, Heilongjiang Qiqihar 161006, China)

This paper presents the simulation study of the aerodynamic force of a square-section bluff body based on the two-dimensional flow field. The aim is to explore the aerodynamic performance of the square-section bluff body under different attack angles. The study provides a reference on how to utilize the aerodynamic performance of the bluff body to improve energy efficiency of the piezoelectric energy harvester. At first, a two-dimensional flow field analysis method is used to obtain the Strouhal numbers for different Reynolds. The results are compared with the experimental data from literature to verify the validation of the analytical method. Subsequently, the aerodynamic force of the square section for different attack angles from 0° to 20° are analyzed, and then the empirical coefficients of the aerodynamic force is obtained by a polynomial curve fitting method. A numerical solution for the galloping piezoelectric energy harvester is achieved to study the effect of the wind speed on the performance of the harvester. The results show that as the attack angle is 8°, the square section shows the best aerodynamic performance. Based on the given parameters, the cut-in wind speed of the piezoelectric energy harvester is 2.6m/s. When the wind speed is 6m/s, the maximal output voltage is 50.95V。

square-section bluff body；Reynolds number；Strouhal number；aerodynamic force

TM619

A

1007-984X(2023)06-0001-04

2023-04-22

齐齐哈尔大学研究生创新训练项目（YJSCX2021088）；黑龙江省省属高等学校基本科研业务费科研项目（145109407）；齐齐哈尔大学教育科研项目（GJQTZX2021007）

王红艳（1974-），女，吉林扶余人，教授，博士，主要从事振动能量收集研究，02080@qqhru.edu.cn。