计及故障重构与信息约束的有源配电网短期可靠性评估方法
王守相,高嘉佐,赵倩宇,张丙杰
(1.天津大学 智能电网教育部重点实验室,天津 300072;2.电力系统仿真控制天津市重点实验室,天津 300072)
0 引言
随着分布式电源大量接入,传统配电网发展成为有源配电网。分布式电源出力的间歇性以及波动性给配电网的可靠运行带来挑战。同时,随着信息技术的广泛应用,配电网依赖信息系统实现实时感知与动态控制。但是信息系统的失效也会反馈于配电网,继而导致配电网故障的发生[1]。为了保证配电网安全运行,对配电网进行可靠性评估的意义重大。
目前,国内外学者在配电网可靠性评估方面已取得一些研究成果。在配电网信息物理系统可靠性建模方面:文献[2]基于广义Petri 网构建了配电网信息物理系统的可靠性评估模型,提升了评估效率;文献[3]考虑信息物理系统的耦合关系与拓扑结构,建立了信息系统与物理系统的元件模型;文献[4]针对基于分布式馈线自动化的配电信息物理系统进行了建模,分析了信息元件失效对配电系统可靠性的影响;文献[5]在考虑信息失效的基础上,研究了分布式电源的作用。在故障后果分析方面,当配电网发生故障后,可以通过协同调度供能设备的出力、储能充放电、电网开关等手段,来实现负荷削减量的最小化。文献[6]在进行故障后果分析时,考虑了故障定位、隔离、恢复的过程;文献[7]考虑故障恢复对用户用电体验的影响,建立了配电网的用电指标评价体系;文献[8]考虑配电网的故障转供,将可靠性与网络规划问题相结合,通过寻优得到可靠性指标。但上述研究均未进行潮流计算,缺少对电压等系统运行状态的关注,评估结果较为理想化。在可靠性评估方法方面,解析法的评估精度高,最小割集法[9]、影响增量法[10]等解析法在可靠性评估中均有应用。但解析法适用于小规模系统,当系统规模较大时,计算时间会呈指数增长。而蒙特卡罗法是常用的模拟方法[3-7],适用于大规模系统,被广泛应用于可靠性评估,但在元件故障率较低或系统故障分析较为复杂时,也存在评估时间过久的问题。而短期可靠性关注系统的运行风险,对评估速度与评估精度均有要求。近年来,机器学习开始被应用于可靠性评估[11-13],提升了评估速度。文献[14]对可靠性评估方法进行总结,提出了“离线建模,在线评估”模式,拓宽了可靠性评估的思路。综上所述,国内外学者在配电网可靠性方面已有较多的研究,但关注的时间尺度大多为中长期,对短期可靠性的研究不足,在信息作用与负荷削减时未考虑潮流计算,对配电网的运行状态有所忽视,难以从系统运行风险的角度给出指导,也无法刻画故障重构等调度措施对系统短期可靠性的影响。而在考虑配电网的运行状态后,又将面临评估时间过久的问题。
为此,本文提出考虑故障重构与信息约束的有源配电网短期可靠性评估方法。首先,根据短期可靠性元件故障率的时变特性,建立基于马尔可夫过程的短期停运模型;然后,在故障后果分析方法方面考虑信息物理耦合与故障重构,提出最优负荷削减策略;最后,针对基于模型驱动的评估方法的耗时过长问题,提出基于最小二乘支持向量机(least squares support vector machine,LSSVM)回归模型的改进方法,在准确性可接受的范围内提升快速性。
1 计及网络重构与信息约束的有源配电网短期可靠性模型
1.1 基于马尔可夫过程的配电网元件短期停运模型
在短期可靠性评估中,元件的状态概率呈时变特性。而在传统可靠性建模中,元件的故障状态概率大多基于历史数据或经验得到,无法体现元件故障的实时特性。马尔可夫过程认为系统下一时刻的状态仅与当前时刻的状态有关,与历史状态无关,适用于刻画元件的时变可靠性模型。假设状态空间为{0,1},0表示正常状态,1表示故障停运状态,λ、μ分别为元件的故障率、修复率。两状态的马尔可夫模型如附录A图A1所示。
在可靠性评估中,元件的无故障工作时间、故障修复时间均服从指数分布,元件状态转移可视为齐次马尔可夫过程。假设元件当前处于正常状态,通过全概率公式可求得元件在时间t后处于状态0 的概率P0(t)和处于状态1的概率P1(t)分别为:
1.2 考虑故障重构与信息物理耦合的有源配电网故障后最优负荷削减模型
在配电网发生故障后,可以通过信息网快速调节分布式电源出力,减少负荷削减量。同时,配电网故障重构与孤岛划分也是实现负荷供应的有效手段。为了尽可能地保障用户的用电,建立考虑故障重构与信息物理耦合的最优负荷削减模型,如式(2)所示。
式中:F为目标函数值;Ne为配电网节点数量;δi为配电网节点i处能够正常供电的负荷比例;θi为配电网节点i的负荷等级权重;Pi为配电网节点i的电负荷。
1.2.1 适用于故障重构与孤岛划分的辐射状拓扑约束
配电网在进行最优负荷削减时,应满足辐射状拓扑约束。一方面,在配电网发生故障后,为了尽可能地恢复供电,并满足非故障区域的正常运行,需要考虑孤岛运行策略;另一方面,当配电网2 处及以上元件发生故障后,可能会出现失电孤岛的情况,这会增加拓扑的复杂性。失电孤岛示意图如附录A 图A2 所示,此时配电网发生3 处故障,节点2、3 处配置了分布式电源,若满足运行条件,则可采用孤岛运行方式进行供电。但节点4、5 无电源供应,成为了失电孤岛。
在网络重构中,常用的父子关系生成树法在某些情况下可能会形成环路,而单商品流约束不允许出现失电孤岛的情况[15],这2 种方法均不适用于考虑故障重构与孤岛划分的可靠性评估。基于生成树约束的有向虚拟多商品流模型通过描述商品在网络中的流通过程来保证网络的连通性,并通过生成树的进一步开断来实现辐射状要求和孤岛划分[16]。该模型可以有效解决形成环路和失电孤岛问题,满足可靠性评估中式(3)—(10)所示对配电网拓扑的灵活性要求。
式中:N为配电网所有节点的集合;B为配电网中所有线路的集合;s为变电站节点;Fk,ij为经过有向线路ij送至节点k的虚拟流量;μij为0-1变量,若有向线路ij被包含在有向生成树中,则μij=1,否则μij= 0;λij为0-1 变量,若有向线路ij的虚拟连接状态为闭合,则λij=1,否则λij= 0;βij为0-1 变量,若线路ij闭合,则βij=1,否则βij= 0。式(3)表示1 个单位虚拟商品由变电站节点流向节点k;式(4)表示节点k获得1个单位虚拟商品;式(5)表示属于节点k的虚拟商品不会流入其他节点;式(6)和式(7)表示当μij构造的有向生成树包含有向线路ij时,虚拟商品才可在该有向线路上流动;式(8)指定了生成树中有向线路的数量;式(9)表示虚拟连接状态由生成树的有向线路决定;式(10)表示支路的实际连接状态由虚拟连接状态约束。
1.2.2 考虑信息物理系统耦合影响的信息约束
信息物理系统中的信息网与配电网相互影响,配电网为信息网提供电能,信息网发出指令来控制配电网中的元件。当配电网节点发生故障时,对应的信息节点会失去供能;当信息节点发生故障时,对应的配电网节点会处于不可控或不可观状态[17]。
当配电网节点因故障发生切负荷时,对应的信息节点能否正常工作可按式(11)所示约束判定[18]。
式中:αi为0-1变量,若信息节点i正常供能,则αi=1,否则αi= 0;Ni为与信息节点i相连接的配电网节点的集合;Pj为配电网节点j的有功负荷需求量;Pcutj为配电网节点j被切除的负荷;φ为信息网与配电网的耦合程度,其取值范围为[0,1],φ取值越大,表明耦合程度越强。
对于采用电力光缆通信的配电网而言,信息网与配电网在空间上存在耦合性,为了简化运算,可认为信息网的拓扑结构与配电网一致,且信息节点由对应的配电网节点供能。基于此,对式(11)进行等价简化,如式(12)所示。
式(12)表示当耦合程度φ不大于δj时,信息节点i被供能。为了便于求解,对式(12)进行如下处理[18]:
当信息节点发生故障时,对应的配电网节点因不可观或不可控需要遵循以下约束:
式中:g为分布式电源节点;Ps,i、Pg,i分别为变电站节点、分布式电源节点的出力;分别为变电站节点、分布式电源节点的出力上限;εj为0-1变量,若信息节点j与信息控制中心(information center,IC)连接正常,则εj=1,否则εj= 0。式(15)表示当信息节点发生故障时,对应的配电网供能节点的供能设备应采取脱网应急处理,停止供能;式(16)表示当信息节点发生故障时,对应的配电网负荷节点无法切负荷。
信息节点保持与IC 连接是该节点正常工作的前提,即:
式中:zjk为0-1 变量,若信息节点j与信息节点k之间的链路连接正常,则zjk= 1,否则zjk= 0;c为IC节点;k1—km为信息节点j与IC 连接路径上的中间节点。式(17)表示当信息节点j与IC 之间至少有1 条通路时,信息节点j连接正常。当信息节点数量较多,信息网拓扑较复杂时,式(17)难以求解。对式(17)进行如下等价变换:
式中:D为信息网中链路的集合;nj为与信息节点j相连的链路数量。式(18)表示IC 节点的连接状态恒为正常;式(19)通过检查其他节点是否与正常工作的信息节点相连来确定其他节点的工作状态。式(19)中存在2 个0-1 变量相乘的非凸项,令0-1 变量wij=εizij,通过McCormick包络[19]进行松弛处理,如式(20)所示。
1.2.3 系统运行约束
基于线路功率的DistFlow 潮流方程适用于描述辐射状配电网。本文采用DistFlow 模型建立配电网约束,并加入切负荷变量、线路连接状态变量反映故障重构。约束条件包括功率平衡约束、线路压降平衡约束、故障线路约束以及电压、电流、功率关系的二阶锥松弛,具体表达式见附录A式(A1)—(A8)。
当配电网发生线路故障后,若所有电源均无法对节点j供电,则该节点的负荷必须被切除;若存在电源可以对节点j供电,则该节点负荷是否被切除由调度决定。按式(19)的处理方式,设置变量γj表征节点j的通电情况,其满足:
式中:u为节点j的上游线路集合;v为节点j的下游线路集合;γj为0-1 变量,若节点j被通电,则γj= 1,否则γj= 0;nj为与节点j相连的线路数量。式(21)表示节点通电与切负荷的关系;式(22)表示电源节点被通电;式(23)通过检查其他节点是否与通电节点相连来确定其他节点的通电状态。式(23)中存在非凸项,令0-1 变量νij=γi βij,亦可通过McCormick 包络进行松弛处理,如式(24)所示。
2 有源配电网短期可靠性评估指标与过程
2.1 短期可靠性指标
短期可靠性评估聚焦于系统短时间运行风险,因此本文选用的可靠性指标为失负荷概率(loss of load probability,LOLP)与供电不足期望(expected energy not supplied,EENS),计算公式分别为:
式中:ELOLP、EEENS分别为考虑分布式电源出力与故障重构策略时的LOLP、EENS 指标值;Pcut为负荷削减量;f(Pcut>0)为负荷削减事件的发生次数;n为蒙特卡罗模拟次数。
为了细化分布式电源出力与故障重构对可靠性水平的影响,选择系统可靠性提升率(system reliability improvement rate,SRIR)指标,其计算公式为:
式中:ESRIR为SRIR 指标值;EEENS0为无分布式电源或采用其他切负荷策略时的EENS指标值。
在基于模拟法的可靠性评估中,EENS的收敛速度慢,本文选择EENS 的方差系数作为收敛阈值,以提高模拟法的精度,其计算公式为:
式中:η为EENS 的方差系数;V(EEENS)为EENS 的方差。
2.2 基于模型驱动的有源配电网短期可靠性评估方法
短期可靠性评估采用小时级时间尺度,在给出当前小时的负荷水平与分布式电源出力后,结合元件短期时变停运概率,通过多次抽样来评估配电网1 d 的可靠性水平。但非序贯蒙特卡罗法为随机抽样,且元件短期停运概率较低,为了满足可靠性指标精度,其所需的抽样次数较多,效率较低。而拉丁超立方抽样法是一种分层抽样方法,抽样效率更高,因此本文选择拉丁超立方抽样法进行抽样。基于模型驱动的有源配电网短期可靠性评估流程见附录A 图A3,具体步骤如下。
步骤1:参数初始化。输入配电网参数以及当前时刻的各元件短期停运概率、负荷水平、分布式电源出力情况。
步骤2:状态抽样。输入系统参数,采用拉丁超立方抽样法,根据元件当前的短期停运概率对配电网元件进行状态抽样,若发生故障,则进入步骤3,若未发生故障,则继续抽样。
步骤3:故障后果分析。根据当前系统的故障情况,结合所提考虑故障重构与信息约束的最优负荷削减模型,对故障后果进行分析,得到对应的负荷削减情况。
步骤4:指标计算。记录本次故障情况,计算可靠性指标。
步骤5:收敛判定。设定最大抽样次数为M,收敛阈值为η0,若EENS 的方差系数小于收敛阈值或达到最大抽样次数,则输出当前时刻的可靠性指标;否则,返回步骤2继续进行抽样。
2.3 基于LSSVM的改进短期可靠性快速评估方法
基于模型驱动的评估方法求解精确,但在快速性方面存在不足。因此,本文采用“离线建模,在线评估”思路提升快速性。 “离线建模,在线评估”是一种模型-数据混合驱动的评估思路,首先通过基于模型驱动的方法获取训练样本,再通过机器学习进行训练,快速输出可靠性指标。
LSSVM 适用于小样本问题,在可靠性评估中已有应用[11,20],因此,本文选用LSSVM 实现可靠性的在线评估。LSSVM的具体原理见附录B。
在选用径向基作为核函数训练样本后,LSSVM训练样本的误差大小由正则化参数r和径向基核函数参数σ决定。本文选用网格搜索法来确定这2 个参数。
“离线建模,在线评估”的可靠性评估流程见附录C 图C1。在离线建模环节,选择不同的负荷水平、分布式电源出力、短期停运概率作为输入数据,将基于模型驱动的可靠性评估方法得到的对应可靠性指标作为输出数据,通过LSSVM 进行训练。该环节多次求解最优负荷削减问题,包含大量的计算,以保证可靠性评估的准确性。在在线评估环节,训练完成后得到LSSVM 回归模型,将未来短期的负荷水平、分布式电源出力情况、短期停运概率作为测试集输入模型,该环节可以迅速得到配电网的可靠性指标,为配电网的运行调度提供实时指导,且在系统状态发生变化时无须重新建模。
3 算例分析
3.1 算例概况
本文采用加入分布式电源的改进IEEE 33 节点配电网为算例,假设信息网拓扑与配电网络一一对应,其拓扑结构见附录C 图C2。选取光伏(photovoltaic,PV)与微型燃气轮机(micro turbine,MT)作为分布式电源接入配电网,设PV 的容量为0.2 MW,MT的容量为0.3 MW,η0=0.05,φ=0.2,元件可靠性参数、配电网节点负荷等级分别见附录C表C1和表C2,配电网典型日负荷曲线见附录C图C3。
3.2 故障后果分析
为了验证本文所提负荷削减策略的有效性,设置以下2 种场景进行故障后果分析:①场景1,20:00时线路12-13、14-15 发生故障;②场景2,12:00 时线路1-2发生故障。
故障后重构结果如图1 所示。场景1、2 的失负荷量分别为0.193、2.216 MW。在场景1中:节点13、14 形成了失电孤岛,完全失去供电,且节点14 所连IC 失效;重构后其余节点均保持与节点6 处的IC 连接,以维持可控性。在场景2 中:变电站与配电网断开连接,造成严重停电;受信息约束影响,重构后节点2 — 33 均保持与IC 连接,并由分布式电源供电,达到了分布式电源的出力上限。
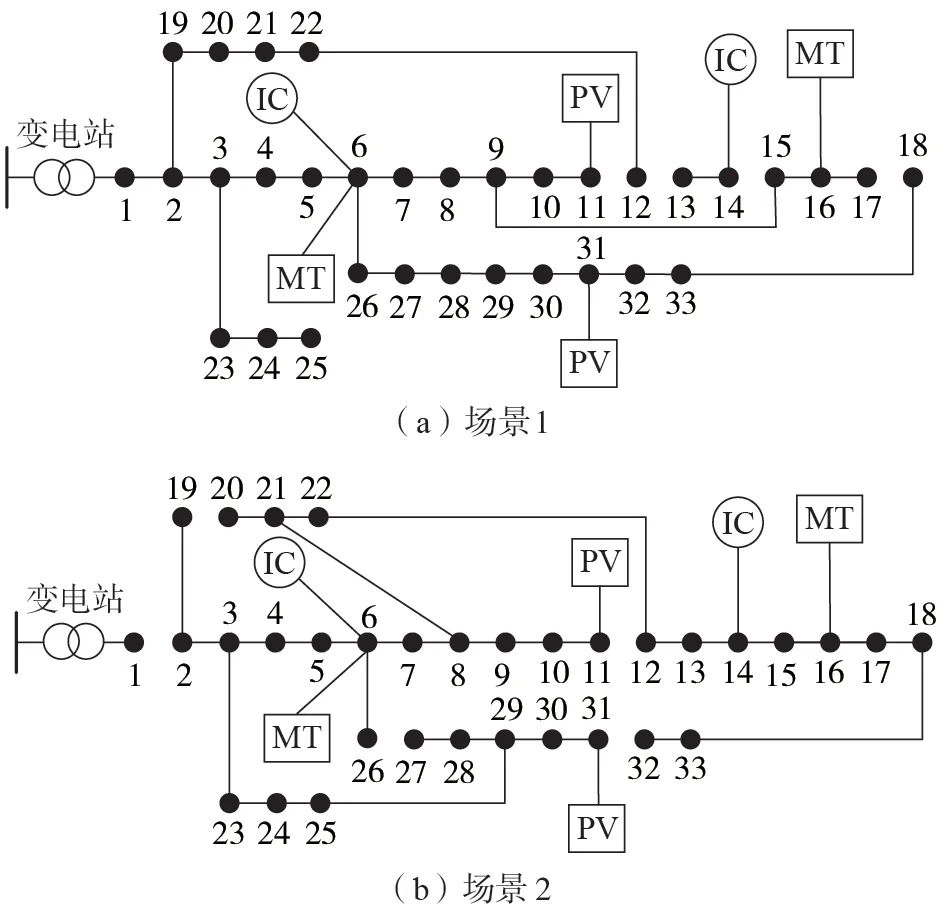
图1 场景1和场景2重构结果Fig.1 Reconfiguration results of Scenario 1 and Scenario 2
以线路15-16 发生故障为例,通过对比分析信息约束在故障后果分析中的作用,考虑、不考虑信息约束时的重构结果如图2所示。
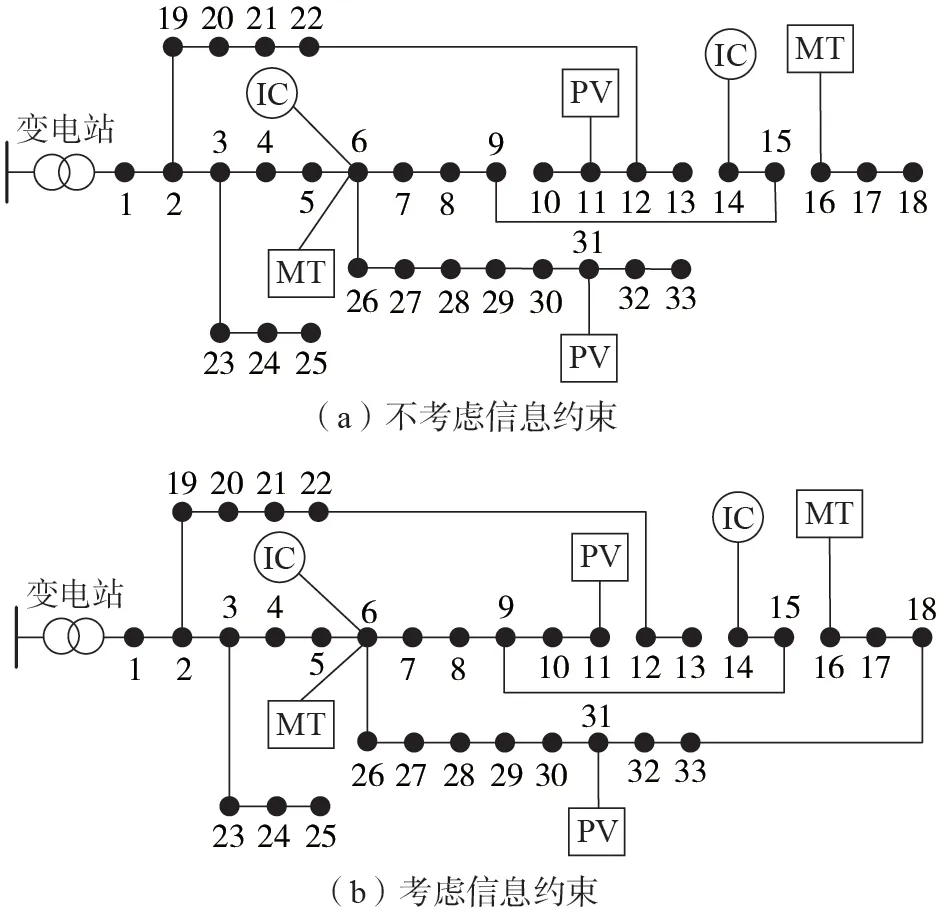
图2 考虑、不考虑信息约束时的重构结果Fig.2 Reconfiguration results considering and not considering cyber constraints
不考虑信息约束时,节点16 — 18 形成了孤岛,通过配置于节点16 处的MT 进行供电。当考虑信息约束后,未形成孤岛,所有节点均与IC 相连。不考虑、考虑信息约束时的切负荷量较接近,分别为0.056、0.061 MW。因此,不考虑信息约束时,重构方案倾向于使用分布式电源对区域进行供电。在考虑信息约束后,重构方案倾向于保证与IC 的相连。虽然考虑信息约束后的切负荷量略微增大,但实际上,在不考虑信息约束的情况下,节点16 — 18形成的孤岛断开了与IC 的连接,其实际负荷恢复量可能无法达到模型计算的理想值。
3.3 可靠性指标分析
以小时为时间尺度,按照基于模型驱动的短期可靠性评估流程对配电网的24 h可靠性水平进行评估,得到的可靠性指标如图3所示。
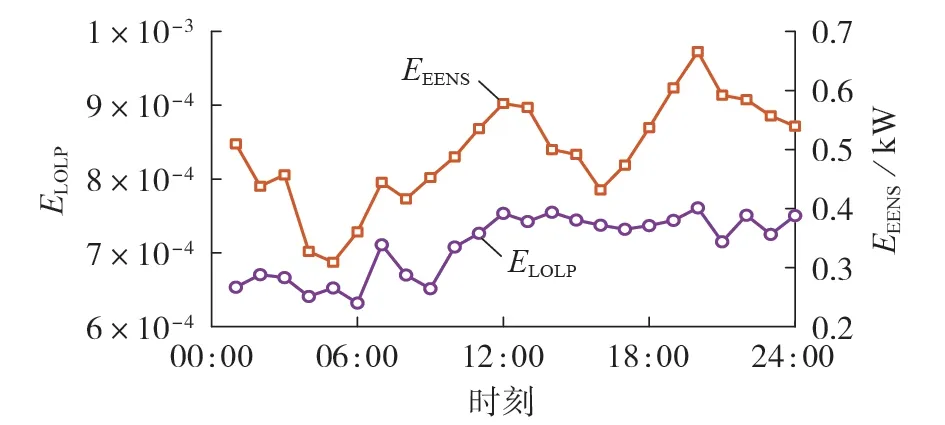
图3 配电网短期可靠性指标Fig.3 Short-term reliability indexes of distribution network
由图3 可知:系统的LOLP 指标呈波动性上升,这是因为元件短期停运概率随时间的增加而增大,但受耦合设备出力、分布式电源出力、负荷水平变化的影响仍有波动;在EENS 指标方面,EEENS总体上与日负荷曲线相近,但受元件短期停运概率、分布式电源出力的影响仍有波动。同时,分布式光伏的出力特性缩小了配电网昼夜的EENS 差距。可靠性指标结果与本文理论分析相符。
在模型驱动法的基础上,采用变化的配电网24 h负荷水平以及对应的元件短期停运概率、分布式电源出力作为输入数据,通过基于模型驱动的短期可靠性评估流程得到输出,共获得432 个训练集样本,并通过LSSVM进行训练。本文的短期可靠性关注的时间尺度为24 h,因此选择配电网典型日作为测试集,共24 个样本。输入典型日24 h 的负荷水平、分布式电源出力、元件短期停运概率后,得到LSSVM在线评估的输出结果。将输出结果与模型驱动法结果进行对比,见表1 与附录C 图C4。模型驱动法的求解时间为46 171.38 s,LSSVM 在线评估的求解时间为0.21 s。结合表1可知,基于LSSVM的评估方法在损失少量精度的情况下大幅加快了求解速度。

表1 LSSVM误差对比Table 1 Comparison of LSSVM error
3.4 可靠性影响因素分析
由前文分析可知,信息物理耦合、分布式电源出力、负荷削减策略都会影响配电网的可靠性。为了细化不同因素对配电网可靠性的影响,并验证本文所提负荷削减策略的优越性,设置5 种场景进行对比分析,场景设置如表2所示。5种场景下配电网的LOLP、EENS指标结果分别如图4和图5所示。
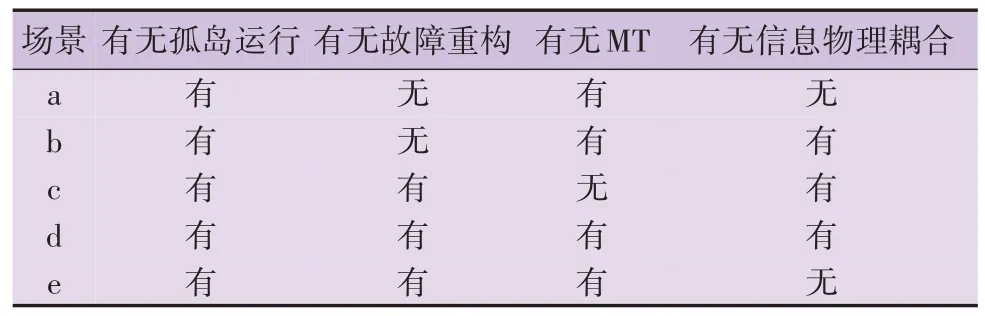
表2 场景设置Table 2 Scenario setting
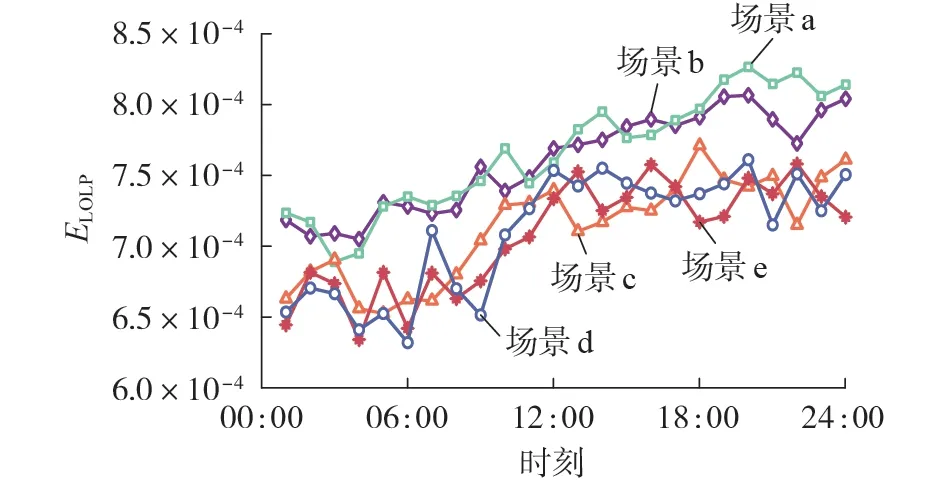
图4 配电网的LOLP指标结果Fig.4 LOLP index results of distribution network
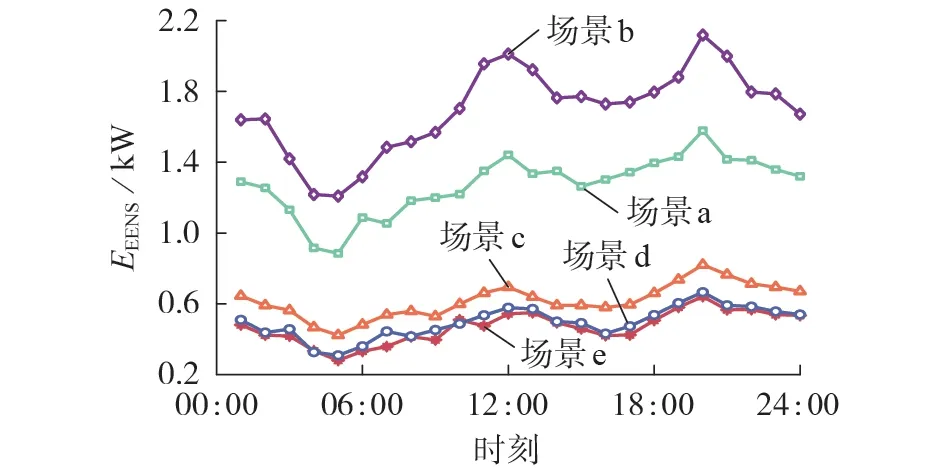
图5 配电网的EENS指标结果Fig.5 EENS index results of distribution network
在场景a 中,进行故障后果分析时未采用本文所提策略,而仅采用孤岛运行策略来进行最优负荷削减,并忽略了信息物理耦合。结果表明,配电网的EENS、LOLP 均处于比较高的水平。这说明仅采用孤岛运行策略的可靠性较低,此时可靠性主要受分布式电源的数量与选址影响。
场景b在场景a的基础上,进一步考虑了信息物理耦合的影响。结果表明,场景b 的可靠性最低。在仅采用孤岛运行策略的情况下考虑信息物理耦合,系统可靠性明显下降。这是因为在孤岛运行状态下,信息节点与IC 的连接可能会断开,继而导致分布式电源出于安全考虑退出运行,进一步增加切负荷量。场景b与场景a的对比结果表明,忽视信息物理耦合影响,会导致评估结果过于乐观。而在计及信息物理耦合影响后,更换负荷削减策略或在规划时增加信息网冗余度是必要的。
场景c 刻画了天然气设备退出运行时的状态,并采用本文所提考虑故障重构与孤岛划分的最优负荷削减策略。与场景a相比,虽然场景c的分布式电源数量减少,但EENS 仍有较大幅度的下降,LOLP也有所下降。这说明在采用本文所提策略后,配电网的负荷削减次数略微减少,且每次削减的负荷量大幅减小,验证了所提策略的有效性。
场景d 采用本文所提策略,并综合考虑了MT 出力与信息物理耦合。与场景b相比,场景d的可靠性大幅提升,表明本文所提负荷削减策略对信息物理耦合影响的抗性较高。与场景c 相比,场景d 的EENS 进一步下降,可靠性有所提升,表明天然气耦合会提升系统的可靠性。考虑故障重构后配电网可以通过联络支路实现负荷的转供电,在一定程度上缓解了分布式电源的压力,因此天然气耦合对可靠性的提升不明显。
与场景d相比,场景e忽略了信息物理耦合。忽略信息物理耦合后,系统的可靠性略微上升。这是因为通信故障可能会导致供能节点与负荷节点失去可控性,从而加大了故障发生后的负荷削减量。而在忽略信息物理耦合的负荷削减策略中,其实际负荷恢复量可能无法达到模型计算的理想值。因此,在可靠性评估中考虑信息约束,可以更加真实准确地反映系统的可靠性水平。
以06:00、12:00、20:00为例,计算这3个时刻不同场景相较于场景b的SRIR,结果如表3所示。结果表明,本文所提策略可以有效提升系统的可靠性水平。
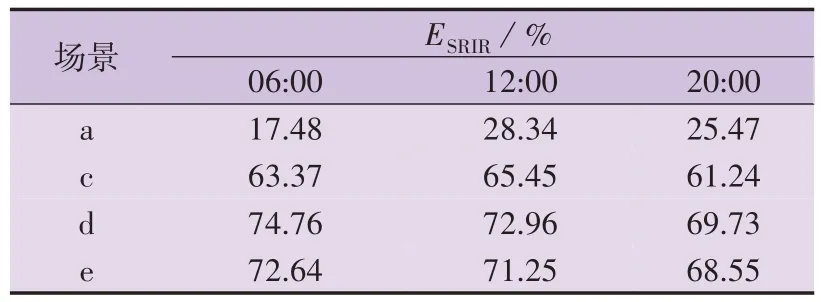
表3 不同场景相较于场景b的SRIRTable 3 SRIR of of different scenarios compared to Scenario b
4 结论
本文基于信息系统与配电系统的耦合,提出了一种计及故障重构与信息约束的有源配电网短期可靠性评估方法。通过在算例分析中对比不同因素对可靠性的影响,得出如下结论:
1)提出考虑信息物理耦合影响的可靠性评估方法,考虑了故障后信息系统与物理系统的相互影响,评估结果表明考虑信息约束后可靠性略微下降,但这更符合实际情况;
2)提出考虑孤岛划分与故障重构的最优负荷削减策略,结果表明所提策略可以有效提升系统的可靠性水平;
3)针对短期可靠性评估对评估速度的要求,通过“离线建模,在线评估”模式,保证了可靠性评估的准确性与快速性。
附录见本刊网络版(http://www.epae.cn)。

