基于重建辅助的压缩学习图像分类

李卫 马骏 辛蕾 李峰,*

基于重建辅助的压缩学习图像分类

李卫1,2马骏1辛蕾2李峰2,*

（1 河南大学软件学院，开封 475100）（2 中国空间技术研究院钱学森空间技术实验室，北京 100094）

压缩感知理论认为可以从少量测量中重建稀疏信号，尽管压缩感知能够实现低成本采样，但其重建过程需要高昂的代价。已有的研究工作成果表明，图像分类可以在测量域进行，而无需重建信号，但目前直接从压缩测量中推理难以提取到深层次特征，无法获得较好的分类效果，针对此问题，为了进一步提升分类结果，文章提出了一种带有重建辅助的深度学习框架直接从图像的压缩测量中推断分类。该框架在分类网络中加入了重建分支作为辅助，联合重建损失与分类损失组合成一个新的加权损失函数调整网络参数，帮助网络提取深层次特征。重建分支只在训练阶段使用来调整网络参数，在训练完成后，重建分支将被舍弃，在实际使用中将不会增加分类任务的时间成本，并保护了数据的隐私。在MNIST和CIFAR-10数据集上进行了实验，结果表明，相比现有方法，所提出的方法在不增加使用成本的情况下有效提高了分类准确度，在两数据集上最高分别提升了1.19个百分点和17.69个百分点，为基于压缩测量的直接推理研究提供了新思路。

压缩感知 深度学习 图像分类 图像重建 辅助任务 压缩学习 遥感应用

0 引言

在对大量信号进行采样且需要节约传输与存储成本的实际应用中，通常需要对原始数字信号压缩，消除冗余信息。但传统高速采样再压缩的方式在采样和压缩阶段都浪费了大量资源。压缩感知（Compressed Sensing，CS）理论的提出打破了这种现状[1-5]。该理论认为如果信号本身具有稀疏性或在某个变换域是稀疏的，那么它可由远低于奈奎斯特采样定理要求的观测值数量重构原信号。CS将采样与压缩融合，在采样时便完成了压缩，规避了以往方法的缺点。对CS采样信号重构往往不是最终目标，人们更关注对采样信号本身所包含信息的处理，如检测、分类等。压缩感知框架下的采样信号的处理工作通常需要两个阶段，第一阶段对信号进行重构，第二阶段对重构信号进行推理。然而CS重构算法往往有着较高的计算成本。因此，直接从压缩测量中推理就变得相当重要。

近年来，关于CS测量直接推断的研究已经取得了一些进展。Haupt等人基于M-ary假设检验研究了CS投影观测在信号分类的应用[6]；Davenport等人研究了直接在压缩感知测量上进行推断的问题，提供了一些理论边界和实验结果[7]；Davenport等人提出了粉碎滤波器[8]，表明如果满足Johnson-Lindenstrauss引理[9]，可以在CS中执行分类任务。之后，不同版本的粉碎滤波器又被研究用于人脸、动作识别[10-11]。Calderbank等人在工作中引入了“压缩学习”（Compressive Learning，CL）一词代表直接在测量领域进行学习而无需付出将数据恢复到高维数据域的代价，其研究在理论上表明，在压缩域上运行的线性支持向量机分类器的性能与在原始信号空间上运行的最佳线性分类器几乎一样好[12]。

深度神经网络近年来发展迅速[13]，Lohit等人首次将神经网络用于从CS测量中直接提取非线性特征[14]。该方法使用观测矩阵获取图像压缩测量值，并通过一个简单的投影操作产生一个原尺寸代理图像作为卷积神经网络（Convolutional Neural Networks，CNN）的输入执行分类推理任务。还提出了两种投影方法，一种是使用转置后的观测矩阵，另一种是使用一个带有可学习参数的全连接层（Fully Connected Layer，FC）。Adler等人提出了一种联合可学习的观测矩阵与推理任务的方法[15]。其使用两个FC分别表示观测矩阵与投影操作，通过联合后续CNN执行分类任务。Xuan等人针对文献[15]的网络结构进行了一些更新，包括激活函数的选择、投影FC的调整以及一个正则化的损失函数等[16]。文献[17]则是在上述工作[14-15]中产生的代理图像上通过一种基于离散余弦变换的方法从中提取二进制特征，并与CNN所提取的特征进行融合执行分类任务，在较低采样量下取得了不错的结果。

这些CL方法都致力于跳过重建阶段，直接从压缩测量中提取特征执行推理任务，来降低计算复杂度与处理时间，同时保护数据的隐私，但相比重建后的数据，直接从压缩测量中进行推理是非常具有挑战性的。目前对于复杂图像压缩测量的分类任务仍然存在准确度较低的问题。是否存在一种折中方案，在保留CL优点的同时加入重建？基于这样的思考，本文提出了一种基于深度学习带有重建辅助的CL框架用于图像分类，该框架在执行分类任务的深度网络中加入了一个重建分支作为分类任务的辅助任务，联合重建损失与分类损失组合成一个新的加权损失函数，通过重建与分类任务共同调整网络参数，帮助网络提取深层次特征。重建分支只在训练过程中使用来调整网络参数，在训练完成后，重建分支将被舍弃，在实际使用中将不会增加网络分类任务的时间成本，且并无实际重建内容的产生，保护了数据的隐私。在MNIST[18]和CIFAR-10[19]数据集上测试了所提出的方法。结果表明，所提出的方法在保留CL优点的同时有效提高了分类准确度。

1 本文方法

本文所提方法在现有框架[14-16]的基础上，加入了重建分支作为辅助任务，在框架结构上与现有方法的区别如图1所示。

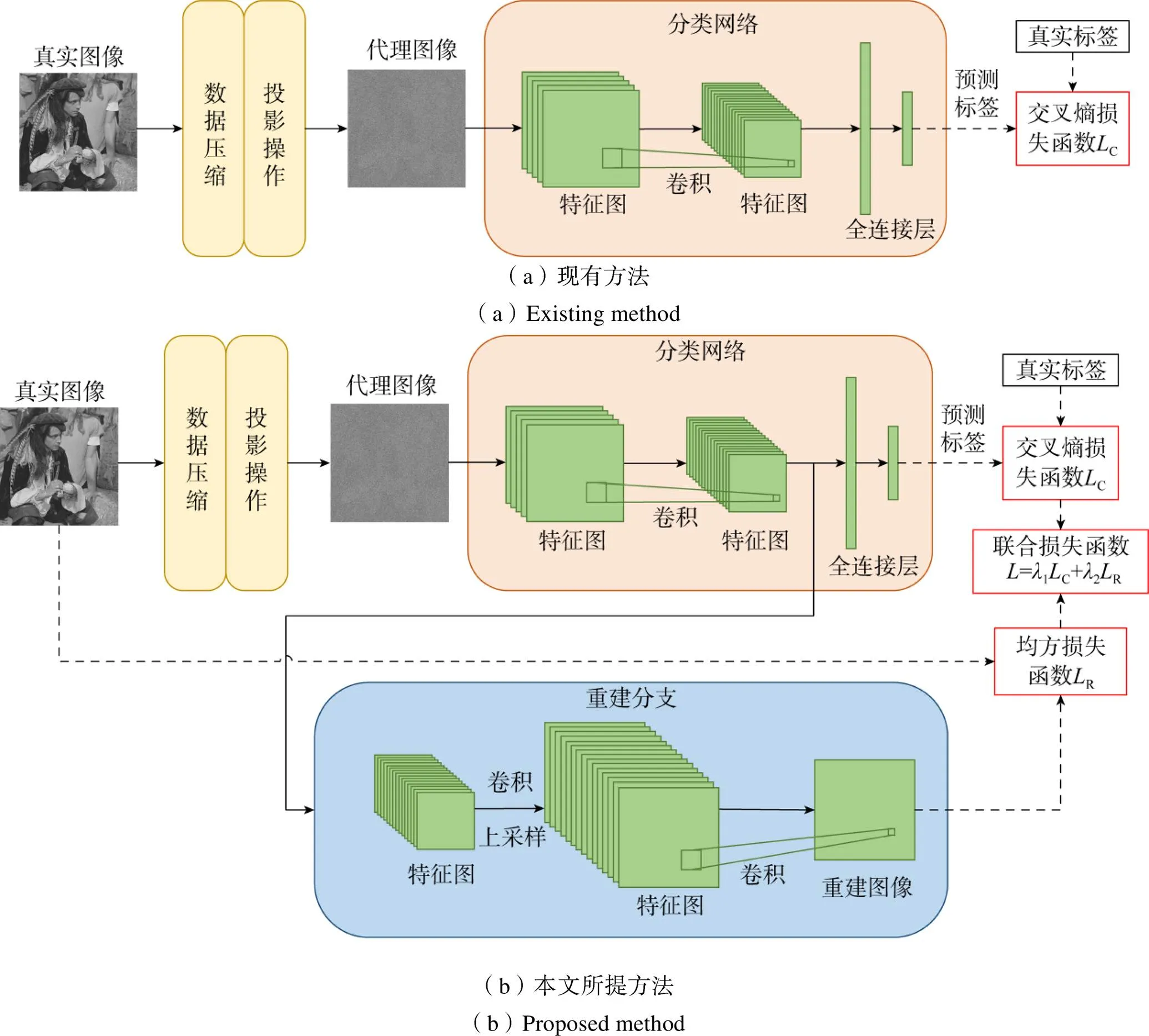
图1 基于深度学习的压缩学习图像分类框架

1.1 压缩与投影

压缩与投影模块主要用于压缩图像数据，以及在进入分类网络前将压缩数据投影回压缩前数据量形成一张代理图像。投影可以看作是替代重建的操作，跳过复杂的重建过程，用一个简单的投影操作来生成一个伪重建图像。其结构如图2所示。

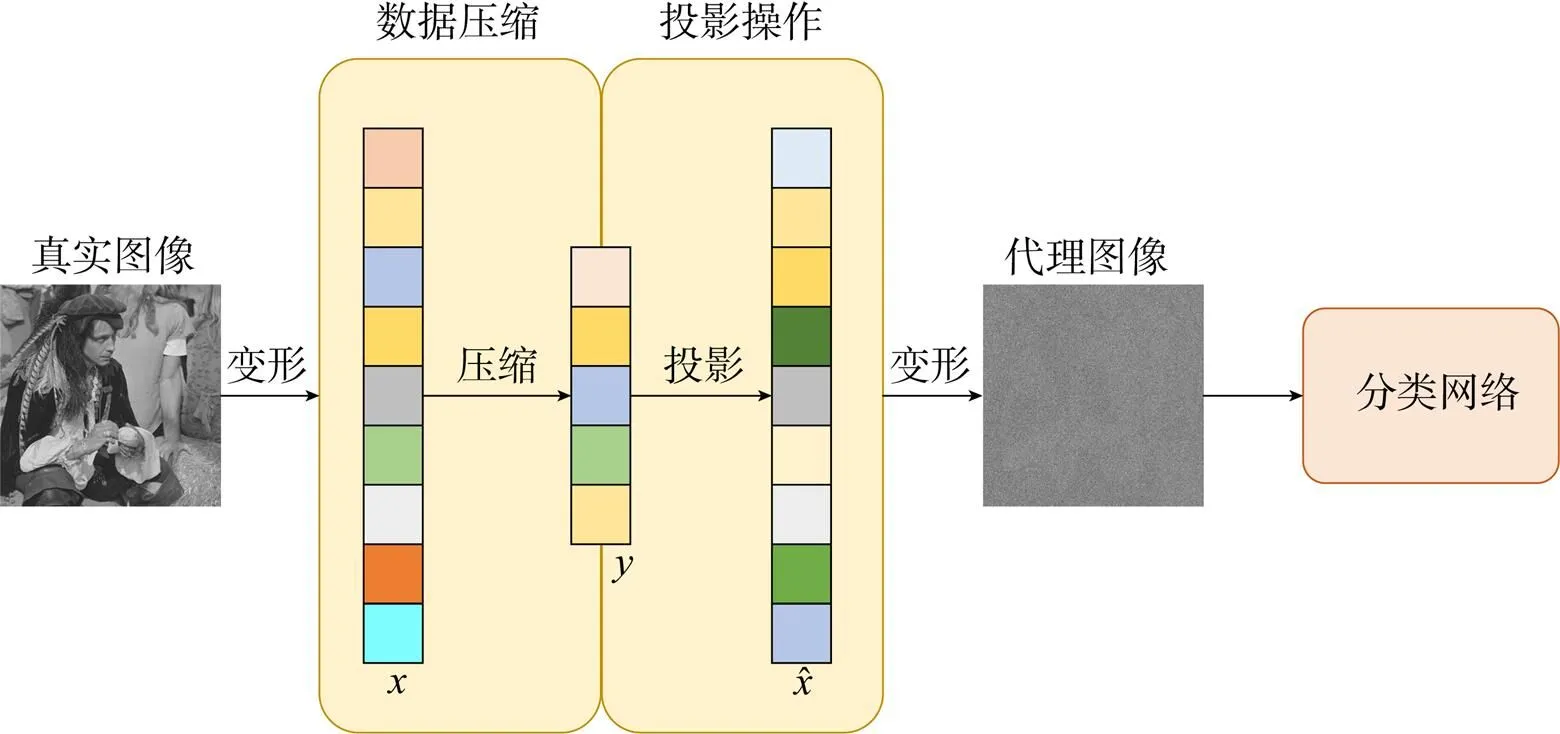
图2 压缩与投影模块的结构

为了验证本文方法的效果，在实验中采用了四种压缩与投影方法。分别将其命名为CP-1[14]、CP-2[14]、CP-3[15]、CP-4。前三种是现有CL方法所采用的压缩与投影方法，CP-4是本文基于CP-3的修改，意在探究代理图像尺寸对本文方法的影响。四种方法如图3所示。

图3 四种压缩与投影方法

CP-1与CP-2在数据获取上采用的观测矩阵是固定的，其优点在于与后续分类网络是分离的，可应用于多种场景，在星上任务中有着较为灵活、广泛的应用。CP-2通过将投影过程可学习化提高了与分类网络的配合，在较少采样数据下取得了比CP-1更好的效果，但在较多采样数据下存在过拟合的问题，相较于CP-1效果差。CP-3通过将观测矩阵与投影过程可学习化，在较少采样数据下取得了比CP-2更好的结果，但在较多采样数据下同样因过拟合问题相较于CP-1效果差，且由于观测矩阵的可学习化，在不同场景需要学习不同的观测矩阵，在星上应用将会受到较大限制。提出CP-4探究尺寸影响是因为较小的代理图像尺寸将会在训练与使用时花费更少的时间成本，具有一定研究价值。以上这些结果差异均来自现有CL方法。

在本文实验中，CP-1和CP-2中的与T使用noiselet[21-22]变换域下的随机采样作为观测矩阵，对采样数据的逆变换作T。

1.2 分类网络

第二部分是分类网络，本文采用较为先进的分类网络之一，宽残差网络（Wide Residual Network，WRN）[23]。WRN是ResNet[24]的一种扩展，比ResNet更注重于缩减长度而加大宽度。网络结构如图4所示。

图4 WRN结构

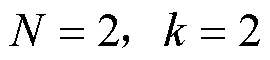
1.3 重建分支

为了使分类网络具有重建能力，将重建分支加入分类网络中。用于图像分类的卷积神经网络通常会通过一系列的池化层来逐步降低特征图的尺寸[23-27]以实现降维与减少计算量，而重建任务最终得到的是一张与真实图像同尺寸的图像。进入重建分支的特征图尺寸是小于原图尺寸的，重建分支用于提升特征图的尺寸到原图尺寸，并对通道降维得到一张图像，最终以真实图像计算损失来调整网络参数。

本文采用亚像素卷积（PixelShuffle）[28]进行上采样操作，PixelShuffle通过对特征图多通道重组来提升图像尺寸，即将多个通道上的特征图拼接在一起，以降低通道数为代价来提升图像尺寸。图5给出了重建分支的具体结构。

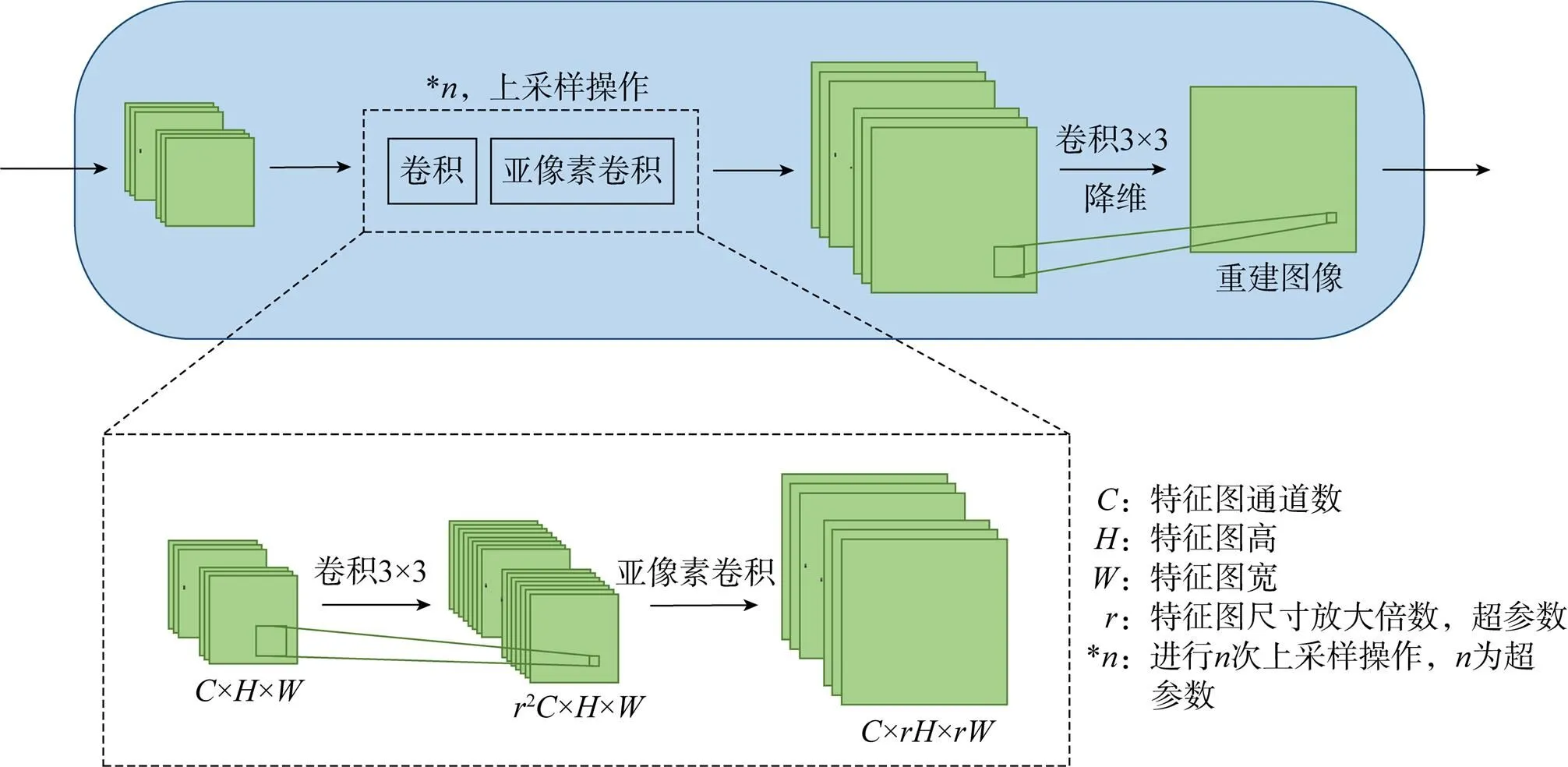
图5 重建分支结构

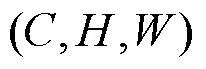
1.4 联合损失函数

现有基于深度学习的CL方法主要通过计算预测标签与真实类别标签之间的损失来求解如下的优化问题进行网络参数的学习。

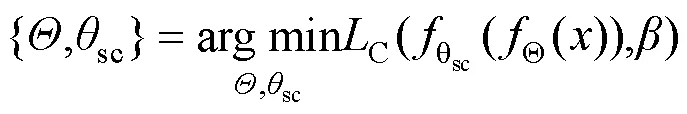
（2）

本文方法框架中的参数分布与正向计算流程，如图6所示。

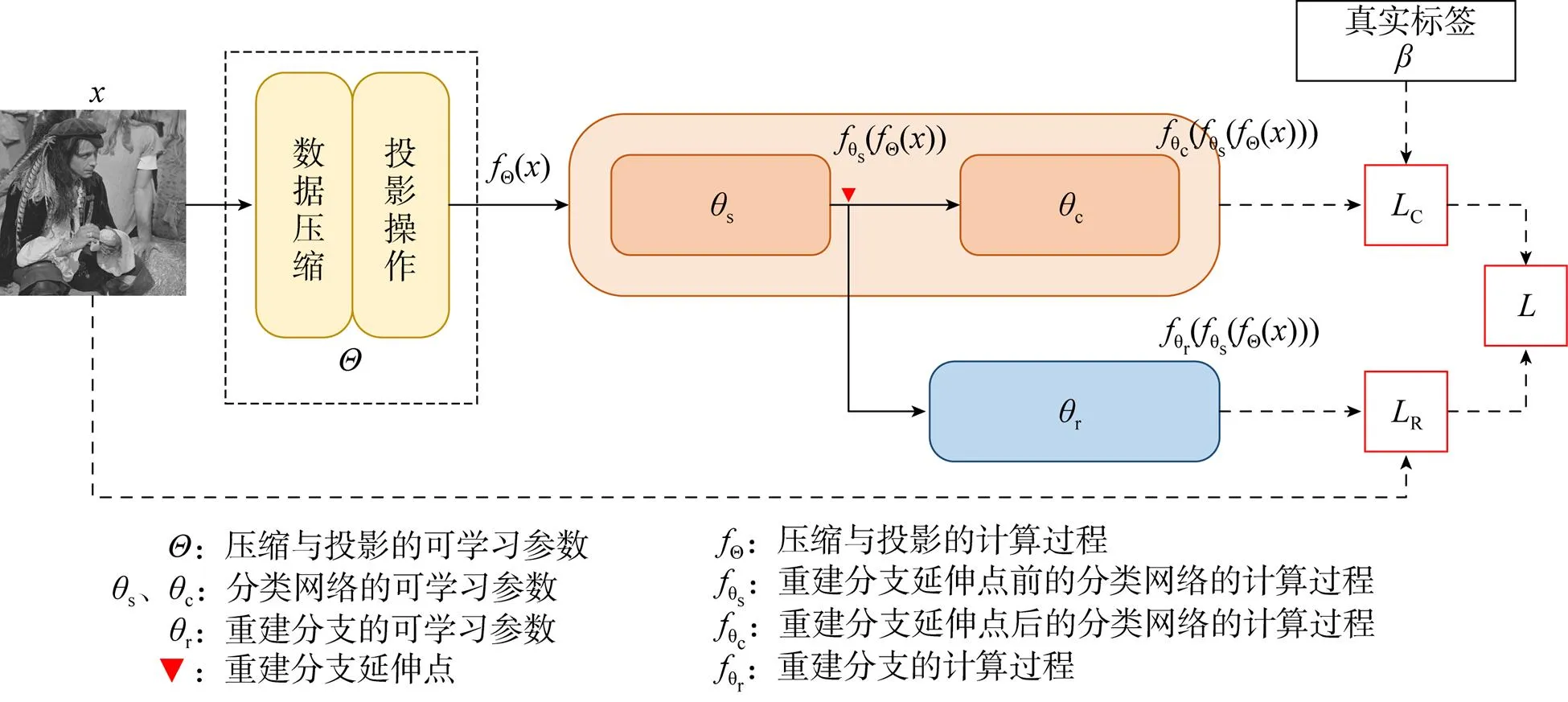
图6 参数分布与正向计算流程

在本文方法中，额外加入了重建分支，整体网络的最终输出变为两部分，且将会计算两个损失，预测标签与真实标签计算损失loss1，重建图像与真实图像计算损失loss2，两个损失的计算可表示为：

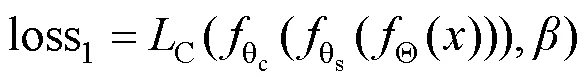
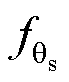
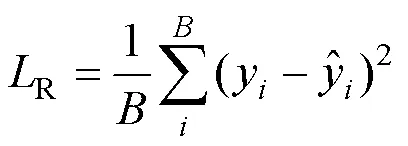
组织蛋白、酸性磷酸酶（ACP）、碱性磷酸酶（AKP）、溶菌酶（LSZ）试剂盒均购买于南京建成生物工程研究院。水蛭素活性测定采用《中国药典》2010版规定的测定方法及陈华友等[12]提供的方法（数据体现时，在相应标号前增加指标英文缩写，如“LSZss”代表配合饲料组嗉囊组织中溶菌酶的活力）。

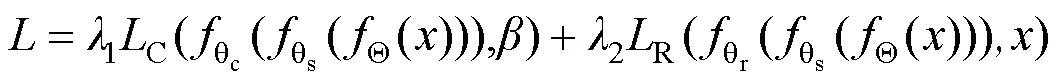
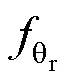
2 实验

2.1 实验设置

实验平台为搭载Ubuntu 18.04.6 LTS系统的计算机。硬件配置：Quadro RTX 5000显卡、IntelRXeon(R) Gold 5218处理器、128GB内存。采用Pytorch深度学习框架。软件配置：Pytorch 1.11.0、Torchvision 0.12.0、CUDA Version：11.4。

实验使用MNIST和CIFAR-10数据集作为实验数据集。训练网络时使用Adam优化器来更新网络参数。批次大小设置为128。总数据训练迭代150轮，初始学习率设置为0.005，每迭代50轮学习率衰减一次，即当前学习率乘以0.1。

实验中分类结果使用准确度作为评测指标，重建结果使用峰值信噪比（PSNR）作为评测指标。准确度为正确分类数与样本总数的比值。PSNR用来计算真实图像与重建图像之间的像素误差，单位为dB，数值越大表明图像重建效果越好。

2.2 数据集与预处理

MNIST数据集是一个手写数字图像数据集，分为10类别，即0到9数字。包含60 000个训练样本和10 000个测试样本，所有图像尺寸为28像素×28像素，且为灰度图像。实验从60 000个训练样本每个类别中随机抽取1 000个样本，共计10 000样本作为验证集，剩余50 000样本作为训练集，原测试样本作为测试集。对原图像采用双三次插值方法上采样到32像素×32像素尺寸用于实验。

2.3 实验结果与分析

实验采用1.1章节中的四种压缩与投影方式，以及两种压缩率压缩数据，分别将数据压缩为原数据量的1/4和1/16，即4倍压缩与16倍压缩，并与WRN结合执行分类任务，对比了现有CL方法在重建分支加入前后的分类准确度。表1和表2分别展示了在MNIST和CIFAR-10数据集上的实验结果。

表1 在MNIST数据集上的分类结果

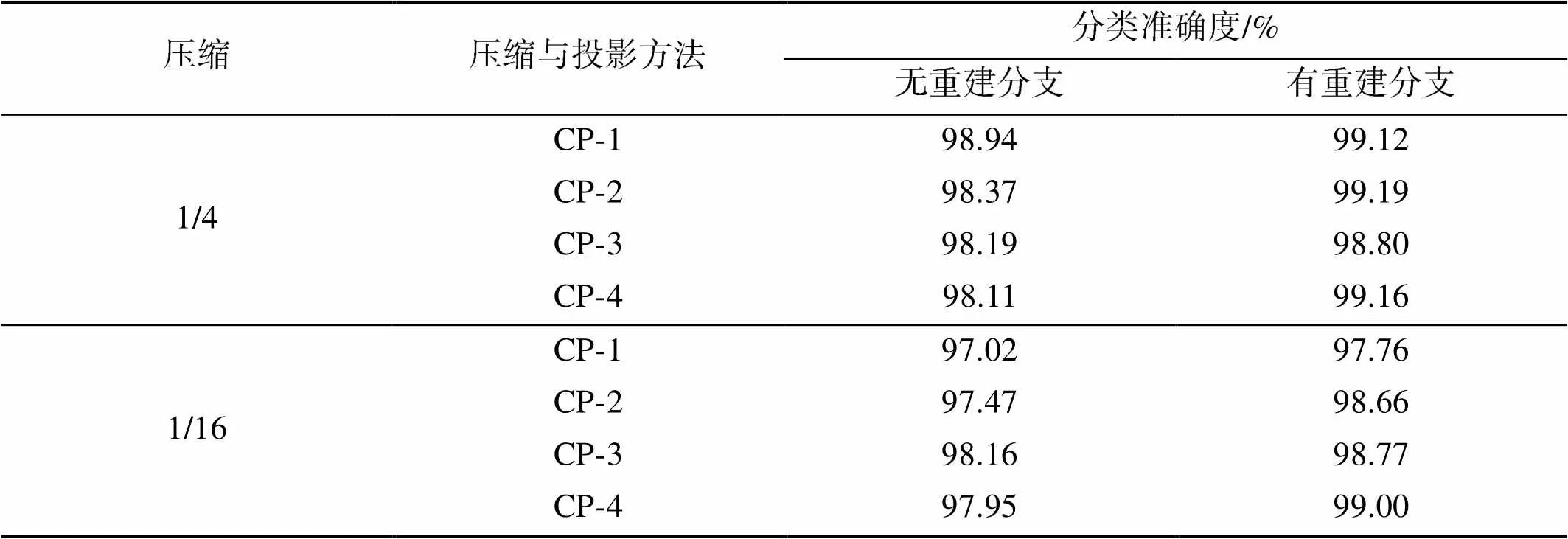
Tab.1 Classification results on the MNIST dataset

表2 在CIFAR-10数据集上的分类结果

Tab.2 Classification results on CIFAR-10 dataset

可以看到，无论在哪种情况下，重建分支的加入都提升了分类准确度。在MNIST上，4倍压缩下最高获得了1.05个百分点的提升，16倍压缩下最高获得了1.19个百分点的提升。在CIFAR-10上，4倍压缩下最高获得了17.69个百分点的提升，16倍压缩下最高获得了10.3个百分点的提升。这些结果充分说明了重建分支优秀的辅助能力，验证了本文方法的有效性。

在两个数据集上，压缩与投影方法若采用FC，则重建分支所带来的提升往往较高，这是因为FC本身具有可学习参数，随着网络优化进行调整，可以与后续网络形成配合，更好地采样数据并从中提取适合网络任务的特征。

对比CP-3和CP-4的结果可以看出，在代理图像尺寸小于原始图像时，重建分支的加入对分类结果都有提升效果。对于简单数据（MNIST），较小的代理图像与重建分支的结合所带来的提升比原始尺寸更高，而对于复杂数据（CIFAR-10），其情况则是相反的。这些结果表明了虽然不同尺寸的代理图像对于重建分支的辅助性能有所影响，但重建分支对于代理图像的尺寸并没有硬性要求，即使尺寸不同也可以发挥出不错的辅助性能。

2.4 损失权重的影响

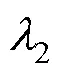
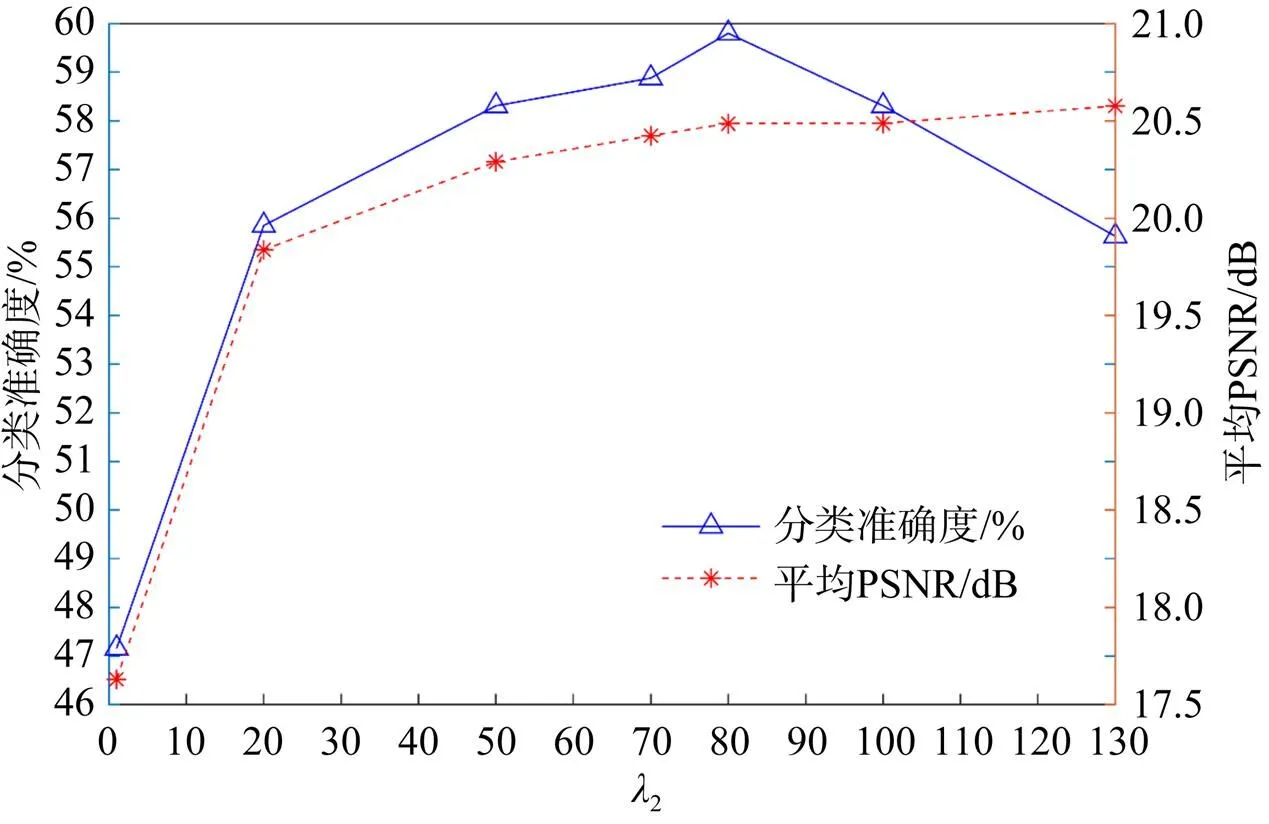
图7 分类准确度与重建图像平均PSNR随超参数变化的曲线图

3 结束语

本文提出了一种基于深度学习带有重建辅助的CL框架，在现有方法框架的基础上，通过加入重建分支来辅助分类任务，并通过一个联合损失函数来优化网络。在MNIST和CIFAR-10两个数据集上进行分类任务实验，结果表明与现有的CL框架相比，在没有增加使用阶段时间成本以及破坏数据隐私性的情况下，本文所提方法提高了分类结果，适合实际应用，也证明了重建分支提取深层次特征的能力。在以后的工作中，如何将重建任务以无成本、低成本的方式加入将会是一个不错的思考方向。

[1] CANDES E J. Compressive Sampling[C]//The International Congress of Mathematicians, Aug 22-23, 2006, Madrid, Spain. 2006: 1433-1452.

[2] CANDES E J, WAKIN M B. An Introduction to Compressive Sampling[J]. IEEE Signal Processing Magazine, 2008, 25(2): 21-30.

[3] DONOHO D L. Compressed Sensing[J]. IEEE Transactions on Information Theory, 2006, 52(4): 1289-1306.

[4] CANDES E, ROMBERG J. Sparsity and Incoherence in Compressive Sampling[J]. Inverse Problems, 2007, 23(3): 969.

[5] CANDES E J, ROMBERG J, TAO T. Robust Uncertainty Principles: Exact Signal Reconstruction from Highly Incomplete Frequency Information[J]. IEEE Transactions on Information Theory, 2006, 52(2): 489-509.

[6] HAUPT J, CASTRO R, NOWAK R, et al. Compressive Sampling for Signal Classification[C]//2006 Fortieth Asilomar Conference on Signals, Systems and Computers, October 9-November 1, 2006, Pacific Grove, CA, USA. IEEE, 2006: 1430-1434.

[7] DAVENPORT M A, BOUFOUNOS P T, WAKIN M B, et al. Signal Processing with Compressive Measurements[J]. IEEE Journal of Selected Topics in Signal Processing, 2010, 4(2): 445-460.

[8] DAVENPORT M A, DUARTE M F, WAKIN M B, et al. The Smashed Filter for Compressive Classification and Target Recognition[C]//Proceedings of SPIE—The International Society for Optical Engineering, 2007, 6498: 142-153.

[9] JOHNSON W B, LINDENSTRAUSS J. Extensions of Lipschitz Mappings into a Hilbert Space[J]. Contemp Math, 1984, 26: 189-206.

[10] LOHIT S, KULKARNI K, TURAGA P, et al. Reconstruction-Free Inference on Compressive Measurements[C]//2015 IEEE Conference on Computer Vision and Pattern Recognition Workshops (CVPRW), June 7-12, 2015, Boston, MA, USA. IEEE, 2015: 16-24.

[11] KULKARNI K, TURAGA P. Reconstruction-Free Action Inference from Compressive Imagers[J]. IEEE Transactions on Pattern Analysis and Machine Intelligence, 2015, 38(4): 772-784.

[12] CALDERBANK R, JAFARPOUR S, SCHAPIRE R. Compressed Learning: Universal Sparse Dimensionality Reduction and Learning in the Measurement Domain[EB/OL]. [2022-09-06]. https://www.researchgate.net/publication/228364241.

[13] 张春晓, 鲍云飞, 马中祺, 等. 基于卷积神经网络的光学遥感目标检测研究进展[J]. 航天返回与遥感, 2020, 41(6): 45-55. ZHANG Chunxiao, BAO Yunfei, MA Zhongqi, et al. Research Progress on Optical Remote Sensing Object Detection Based on CNN[J]. Spacecraft Recovery & Remote Sensing, 2020, 41(6): 45-55. (in Chinese)

[14] LOHIT S, KULKARNI K, TURAGA P. Direct Inference on Compressive Measurements Using Convolutional Neural Networks[C]//IEEE International Conference on Image Processing (ICIP), September 25-28, 2016,Phoenix, AZ, USA. IEEE, 2016: 1913-1917.

[15] ADLER A, ELAD M, ZIBULEVSKY M. Compressed Learning: A Deep Neural Network Approach[EB/OL]. [2022-09-06]. https://arxiv.org/pdf/1610.09615.pdf.

[16] XUAN V N, LOFFELD O. A Deep Learning Framework for Compressed Learning and Signal Reconstruction[C]//5th International Workshop on Compressed Sensing Applied to Radar, Multimodal Sensing, and Imaging (CoSeRa), September 10-13, 2018, University of Siegen, Germany. 2018: 1-5.

[17] DEGERLI A, ASLAN S, YAMAC M, et al. Compressively Sensed Image Recognition[C]//7th European Workshop on Visual Information Processing (EUVIP), November 26-28, 2018, Tampere, Finland. IEEE, 2018: 1-6.

[18] LECUN Y, BOTTOU L, BENGIO Y, et al. Gradient-Based Learning Applied to Document Recognition[J]. Proceedings of The IEEE, 1998, 86(11): 2278-2324.

[19] KRIZHEVSKY A, NAIR V, HINTON G. The CIFAR-10 Dataset[EB/OL]. [2022-09-06]. http://www.cs.toronto.edu/～ kriz/cifar.html.

[20] GLOROT X, BORDES A, BENGIO Y. Deep Sparse Rectifier Neural Networks[C]//Proceedings of the Fourteenth International Conference on Artificial Intelligence and Statistics, 2011, 15: 315-323.

[21] WEN J, CHEN Z, HAN Y, et al. A Compressive Sensing Image Compression Algorithm Using Quantized DCT and Noiselet Information[C]//Proceedings of the 2010 IEEE International Conference on Acoustics Speech and Signal Processing (ICASSP), March 14-19, 2010, Dallas, TX, USA. IEEE, 2010: 1294-1297.

[22] PASTUSZCZAK A, SZCZYGIEL B, MIKOLAJCZYK M, et al. Modified Noiselet Transform and Its Application to Compressive Sensing with Optical Single-Pixel Detectors[C]//18th International Conference on Transparent Optical Networks (ICTON), July 10-14, 2016, Trento, Italy. IEEE, 2016: 1-4.

[23] ZAGORUYKO S, KOMODAKIS N. Wide Residual Networks[EB/OL]. [2022-09-06]. https://arxiv.org/pdf/1605.07146.pdf.

[24] HE K, ZHANG X, REN S, et al. Deep Residual Learning for Image Recognition[C]//2016 IEEE Conference on Computer Vision and Pattern Recognition (CVPR), June 27-30, 2016, Las Vegas, NV, USA. IEEE, 2016: 770-778.

[25] HUANG G, LIU Z, MAATEN L V D, et al. Densely Connected Convolutional Networks[C]//2017 IEEE Conference on Computer Vision and Pattern Recognition, July 21-26, 2017, Honolulu, HI, USA. IEEE, 2017: 2261-2269.

[26] KRIZHEVSKY A, SUTSKEVER I, HINTON G E. Imagenet Classification with Deep Convolutional Neural Networks[J]. Communications of the ACM, 2017, 60(6): 84-90.

[27] SIMONYAN K, ZISSERMAN A. Very Deep Convolutional Networks for Large-Scale Image Recognition[EB/OL]. [2022-09-06]. https://arxiv.org/pdf/1409.1556.pdf.

[28] SHI W, CABALLERO J, HUSZAR F, et al. Real-Time Single Image and Video Super-Resolution Using an Efficient Sub-Pixel Convolutional Neural Network[C]//2016 IEEE Conference on Computer Vision and Pattern Recognition (CVPR), June 27-30, 2016, Las Vegas, NV, USA. IEEE, 2016: 1874-1883.

Image Classification Based on Reconstruction Assisted Compressive Learning

LI Wei1,2MA Jun1XIN Lei2LI Feng2,*

（1 College of Software, Henan University, Kaifeng 475100, China）（2 Qian Xuesen Space Technology Laboratory, China Academy of Space Technology, Beijing 100094, China）

Compressive sensing theory suggests that sparse signals can be reconstructed from a small number of measurements. Although compressive sensing enables low cost sampling, its reconstruction process is costly. Recent work has shown that image classification can be performed in the measurement domain without reconstruction of the signal, but it is currently difficult to extract deep features for better classification by inference directly from compressed measurements. To address this problem and to further improve the classification results, the article proposes a deep learning framework with reconstruction assistance to infer classification directly from compressed measurements of images. The framework adds a reconstruction branch to the classification network as an aid, and the joint reconstruction and classification losses are combined into a new weighted loss function to adjust the network parameters. The reconstruction branch is only used during the training phase to adjust the network parameters, and is discarded after training is complete, which in practice will not increase the time cost of the classification task and protects the privacy of the data. Experiments were conducted on the MNIST and CIFAR-10 datasets, and the results show that the proposed method effectively improves the classification accuracy without increasing the cost of use, by up to 1.19 and 17.69 percentage points on the two datasets respectively, providing a new idea for direct inference studies based on compressed measurements.

compressive sensing; deep learning; image classification; image reconstruction; auxiliary task; compressive learning; remote sensing application

TP75

A

1009-8518(2023)05-0105-11

10.3969/j.issn.1009-8518.2023.05.012

李卫，男，1995年生，2018年获河南大学软件工程专业学士学位，现在河南大学电子信息专业攻读硕士学位。主要研究方向为压缩学习、图像分类。E-mail：lwei@henu.edu.cn。

2022-09-06

科技部重点研发计划（2020YFA0714100）

李卫, 马骏, 辛蕾, 等. 基于重建辅助的压缩学习图像分类[J]. 航天返回与遥感, 2023, 44(5): 105-115.

LI Wei, MA Jun, XIN Lei, et al. Image Classification Based on Reconstruction Assisted Compressive Learning[J]. Spacecraft Recovery & Remote Sensing, 2023, 44(5): 105-115. (in Chinese)

（编辑：庞冰）