基于最优训练期的风力预报小时级订正释用方法

刘菡，於敏佳

（舟山市气象局，浙江舟山 316000）

0 引言

近年来，随着社会经济的持续发展，传统的气象预报产品已较难满足政府部门、市场企业和社会公众与日俱增的精细化、数智化要求，因此急需研发时空精密、预报精准、数字智慧的预报产品。风力预报事关临港产业、渔业捕捞、航线运输的安全与发展，因此精细化的风力预报小时级订正释用技术研究至关重要。

目前风力预报的订正释用方面已有较多成果。钱燕珍等[1]将支持向量机（Support Vector Machine，SVM）回归方法应用于近海和登陆热带气旋的强度预报；胡海川等[2]利用概率密度匹配方法对我国近海10 m 风预报进行修正；杨晓君等[3]将BP（Back Propagation）人工神经网络引入到渤海海风的预报订正中；赵文婧等[4]应用相似误差订正方法订正了短期风速预报；杨程等[5]基于偏最小二乘回归方法开展了区域风速预报订正技术研究；刘鸿升等[6]设计了最大值-阀值综合集成法并实现偏北大风的数值预报释用；李江萍等[7]初步探讨了基于统计降尺度方法的数值预报产品释用技术。以上方法都取得了一定的订正释用效果，可应用于实际业务中。

但是，风力预报精细化方面的成果相对较少。美国从2003 年开始最早发展了国家数字预报数据库[8]，可提供逐1h更新、2.5 km/5 km 分辨率的无缝隙网格天气预报。德国基于强大的数值模式能力，利用多个模式解释应用和统计后处理预报的优化集成预报方法，提供逐5 min 更新、2.5 km 分辨率的分钟级—延伸期30 d 的订正网格预报[9]。陈豫英等[10]采用多元线性和逐步回归的MOS 统计方法进行风的精细化释用；杨程等[11]将站点监测资料和数值模式产品应用统计回归和数据融合技术，对近地面风速产品进行精细化修正；荣艳敏等[12]采用逐步回归的模式输出统计方法（Model Output Statistic Method，MOS）方法，针对山东12 个海区指标站的风速进行模式产品的解释应用；董美莹等[13]探讨了欧洲中期天气预报中心（European Centre for Medium-Range Weather Forecasts，ECMWF）驱动场水平风场谱逼近技术对浙江台风精细化预报性能的影响。上述方法均表明可以用数理统计方法对固定间隔时次的预报进行订正释用。於敏佳等[14]利用最大风速与极大风速的关系和逐时加权滚动订正的方法对风力预报进行了逐小时的精细化订正释用，但此方法需逐时滚动更新。因此，本文将进一步探究适用于日常业务的定时一次性输出的风力预报小时级订正释用技术。

1 资料和方法

1.1 资料说明

风力预报资料采用浙江省气象局的Fruit细网格产品。该产品是针对中国气象局下发的ECMWF产品全要素的整合和缩容产品，模式起报时间是20 时（北京时，下同），资料覆盖区域为0°～60°N，60°～150°E，时间分辨率为3 h，预报时效为0～240 h，空间分辨率为0.125°×0.125°。选取时间段为2020年1月1日—2021年1月1日每日20时的起报场预报数据。

实况最大风速和极大风速资料来自浙江省自动气象站嵊泗国家基准站、定海国家基本站、普陀国家一般站、岱山国家一般站和舟山浮标站。站点位置见图1。这些站点代表性强，数据完整，经人工剔除了异常值并消除了缺测记录，数据较为真实可靠。数据选取时间段为2012 年1 月1 日—2021 年1月1 日，其中2012—2020 年的数据资料用于最大风速与极大风速关系分析，2020—2021 年数据资料参与最优训练期计算，并作为独立样本进行检验。

图1 指标站站点位置图Fig.1 Location of index stations

1.2 订正释用方法

分三步对浙江省气象局的Fruit 细网格产品进行订正释用。第一步将Fruit细网格产品逐3 h 风力预报线性插值至逐小时；第二步对照实况最大风速选定最优模型，计算得出各预报时效（0～72 h）的最优训练期，并对各预报时效的风力预报进行订正；第三步套用最大风速与极大风速的关系，最终得出基于最优训练期的订正释用后的逐小时极大风速预报。

1.3 效果检验方法

对于训练方法的检验，除了分析风力预报误差的订正效果外，在实际业务中的可应用性也尤为重要。计算得出稳定的各预报时效对应的最优训练期是业务可应用的关键。在误差订正效果方面，利用最优训练期逐小时计算各预报时效（0～72 h）的订正释用效果。结果用修正率（Cri）表示:

式中：MAE0i为各预报时效（0～72 h）采用日常实际业务惯用的人工经验所得的极大风（如最大风速为5～6 级对应极大风速为7 级）与实况极大风的平均绝对误差；MAE1i为各预报时效（0～72 h）经本文方法订正释用后的极大风平均绝对误差。

2 最大风速订正

2.1 最大风速订正方法

2.1.1 线性回归

该方法分整年、半年、季度、单月4种方案（以下简称4 种方案），利用前一日20 时—当日05 时10 个时次的预报实况偏差，取当日06 时前的2～10 个时次，共9种训练期，建立预报时效与预报实况偏差的一元线性回归方程。方程为：

式中：En为第n个预报时效的预报实况偏差；Tn为第n个预报时次；a为回归系数；b为常数项；a、b通过最小二乘法求解。

2.1.2 加权误差

按照4种方案，利用前一日20时—当日05时10个时次的预报实况偏差，取当日06 时前的2～10 个时次，共9 种训练期，计算前一日20 时—后一日20时所有预报时效（0～72 h）的加权误差：

式中：E为加权误差；En为当日06时前n个预报时次的预报实况偏差；an为对应时次预报偏差的权重，且an为大于0且和为1的等差数列；d为公差。

假设：越靠近06时（预报时次）的预报实况偏差（前一日20时—当日05时）越具参考性，则d<0。

根据设定，求a1和d的取值范围并取值：

因为a1+a2+...an= 1，且an为大于0 的等差数列，所以

因为an=a1+(n- 1)d>0，= 1，将代入式（4），则

2.1.3 平均误差

按照4种方案，利用前一日20时—当日05时10个时次的预报实况偏差，取当日06 时前的2～10 个时次，共9 种训练期，计算前一日20 时—后一日20时所有预报时效（0～72 h）的平均误差。计算公式为：

式中：E为平均误差；En为当日06时前n个时次的预报实况偏差。

2.2 方法对比

2.2.1 订正效果

按照4种方案设计线性回归、加权误差、平均误差3种训练方法，取当日06时前的2～10个时次，共9 种训练期，计算各站点各预报时效（0～72 h）的最优训练期及对应的最小平均绝对误差。结果表明（见图2），3 种方法对风力预报误差都有改进，其中线性回归法表现出较为平稳的小波动性，加权误差法和平均误差法在0～15 h 之间波动幅度较大，这表明两种方法对于0～15 h 预报时效具有明显的订正效果（在10 h处最大风速绝对误差达到0.2 m/s的精度），11 h 后订正误差快速增加，直到15 h 处回归小波动性缓慢增加的态势。因此，0～15 h加权误差法和平均误差法的风力预报误差改进优于线性回归法，具备更好的临近预报订正效果。

图2 各训练方法0～72 h预报时效订正前后站点风力误差对比和最优训练期分布Fig.2 Comparison of wind force errors and distribution of optimal training period before and after correction of 0～72 h forecast time of each training method

图2 （续）Fig.2 （Continued）

对比分析5 个站点的订正效果。地形方面，定海地形遮蔽最为严重，模式预报原误差也最大，岱山、普陀次之，嵊泗遮蔽少，舟山浮标四面开阔，代表性最好。风力预报误差方面，与嵊泗、舟山浮标相比，岱山、普陀常年风力小，原预报误差相对较小；定海原风力预报误差存在24 h 的周期变化性，其中大致在12～24 h、36～48 h、60～72 h 存在明显的日变化特征，且每日12 时达到最小，具备一定的规律性，加权误差法和平均误差法并不适用，在原误差最小的时次订正误差反而较大，而线性回归法则抹去了原误差的日变化性，订正效果相对较优。

综上分析可知，0～15 h 加权误差法和平均误差法的风力误差订正效果明显优于线性回归法，15 h 后3 种方法订正效果相差较小；但对于受地形遮蔽较大且原误差存在日变化的站点，线性回归法优于加权误差法和平均误差法。

2.2.2 业务应用

图2 还展示了3 种方法的最优训练期。线性回归法最优训练期以2 h 和10 h 为主，但各站点存在差异，且同一站点各预报时效的最优训练期也变化较大。加权误差法和平均误差法在各个站点的表征一致，最优训练期都以10 h 居多，在0～10 h 预报时效内最优训练期从10 h快速递减到2 h，而在10～20 h预报时效内最优训练期又出现快速递增。

图3 为4 种方案在9 种训练期（2～9 h）下计算的各预报时效（0～72 h）的平均绝对误差。结果表明，线性回归法误差发散，最优训练期不稳定，没有可用于日常业务预报的最优训练期。加权误差法和平均误差法的结果大致相同，误差不发散，最优训练期稳定，可将10 h 作为0～5 h 和20 h 后预报时效的最优训练期，但5～20 h 预报时效的最优训练期并不明确。

图3 各站点0～72 h预报时效平均绝对误差分布Fig.3 Distribution of mean absolute error of 0 to 72 h forecasts at each station

分别计算了在4 种方案下利用3 种方法得到的5 个站点（每个方法共20 个样本总量）各预报时效（0～72 h）的最优训练期的概率分布。从图4 可以看出，线性回归法的最优训练期分布散乱，以2 h 和10 h为主，除7～11 h预报时效对应的最优训练期概率达50%以上外，其余预报时效均较低，无法给定各预报时效的最优训练期；加权误差法对0～5 h、23～72 h 预报时效的最优训练期分布有明晰表现，6～10 h、16～22 h 预报时效的最优训练期概率也都大于50%，但仍有5个预报时效（11～15 h）的最优训练期分布相对较广，其中11～12 h 预报时效的最优训练期以2 h 为主，13 h 预报时效以4 h 为主，14～15 h预报时效以10 h为主；平均误差法则对0～10 h、16～72 h 预报时效的最优训练期分布有明晰表现，11～12 h预报时效的最优训练期以2 h为主，13 h预报时效以4 h为主，14～15 h预报时效以10 h为主。

图4 各方法预报时效最优训练期概率分布Fig.4 Probability distribution of optimal training period of each prediction time

总体而言，线性回归、加权误差、平均误差3 种方法在业务应用层面效果递进。线性回归法各预报时效的最优训练期散乱且无法确定，业务应用效果差；加权误差法对0～5 h、23～72 h预报时效的最优训练期表现明晰，平均误差法则将明晰范围进一步扩大到0～10 h 和16～72 h 预报时效，但两者在11～15 h预报时效都未给出绝对大概率值，根据概率分布可知，2 h、4 h、10 h 分别为11～12 h、13 h、14～15 h 预报时效的最大概率最优训练期。

3 最大风速与极大风速关系

对于最大风速与极大风速的关系，目前已有较多研究[15-24]。对各站点以一元线性方程进行拟合，并计算相关系数和绝对误差，结果见表1。最大风速与极大风速较好地符合y=ax+b的一元线性关系，在没有地形影响的开阔海面上，舟山浮标的相关系数更是高达0.99。

表1 站点拟合方程和效果检验Tab.1 Site fitting equation and effect test

3.1 地形影响

最大风速与极大风速的关系与地形密切相关。地形作用主要包括山体阻挡、爬坡、狭管效应、绕流等，都会对风力的阵性产生影响。各县区测站16风向最大风速与极大风速拟合方程各不相同（见图5a—c），所拟合的一元线性方程中的常数项仍相对较小，最大的也仅有0.84，在推算极大风速时，也仅有不到1 m/s的影响，可见在以最大风速推算极大风速时，起主导作用的是一元线性方程y=ax+b中的一次项系数a（即风力阵性系数）。嵊泗、岱山、定海、普陀4 个县区本站分16 风向的系数a分别为1.18～1.58、1.40～1.93、1.60～2.15、1.43～1.91，当最大风速达到13.9 m/s（风力为7 级）时，4 个县区本站在16 风向上的极大风速最大差可达5.56 m/s、7.37 m/s、7.65 m/s、6.67 m/s；而对舟山浮标分16风向进行分析发现（见图5d），该海上浮标站16风向的阵风系数基本稳定在1.11～1.15，各风向上的最大风速与极大风速关系基本一致。由此可见，地形的作用致使各个风向上风力阵性差异明显，风向不同，阵性系数a也不同，a差异越大，则风力的阵性差异也越大。

图5 嵊泗、岱山、定海、舟山浮标16风向最大风速与极大风速关系对比图Fig.5 Correlation between maximum and extreme wind speeds at Shengsi,Daishan,Dinghai and Zhoushan buoys

3.2 下垫面影响

相较于陆地和沿海粗糙的硬地下垫面，海上下垫面为光滑水面，在大尺度运动中，海上空气质点的运动较遵从地转风规则。对比2012 年1 月—2020 年1月嵊泗、岱山、普陀、定海4个县区本站和舟山浮标站16风向的实况最大风速与极大风速之差，发现4 个县区本站相差较小（差值分别为2.51 m/s、2.37 m/s、2.37 m/s、2.51 m/s），而舟山浮标站的平均差仅为0.91 m/s。在各个风向上，舟山浮标的风力阵性都明显小于硬地站点（见图6），因此下垫面也是直接影响风力阵性系数a的因子之一。

图6 嵊泗、岱山、定海、普陀、舟山浮标16风向最大风速与极大风速之差对比Fig.6 Comparison of maximum and extreme wind speeds at Shengsi,Daishan,Dinghai,Putuo and Zhoushan buoys

3.3 天气系统影响

当有台风、冷空气、低压等系统影响时，最大风速与极大风速的差异往往较大，能达到8 m/s 甚至10 m/s 以上，这与同等气压梯度条件下的最大风速与极大风速之差有较大差别。对2012—2020 年在低压、冷空气、台风3个系统影响下对应时次的最大风速和极大风速进行拟合发现（见图7），嵊泗、岱山在各系统影响下的差异比较小，岱山站的阵性系数基本都在1.5 左右，嵊泗的阵性系数基本在1.2 左右；而定海和普陀的差异比较大，低压和冷空气在定海站的阵性较强，阵风系数高达1.85 和1.9，定海台风的阵性系数仅为1.59。舟山浮标低压、冷空气和台风的阵性系数分别为1.14、1.15、1.2，结果较为接近，舟山浮标不分影响系统的阵风系数也为1.14。因此可以看出，各天气系统对于陆地和沿海风力的阵性有影响，而在开阔的渔场上，各天气系统的风力阵性基本一致。

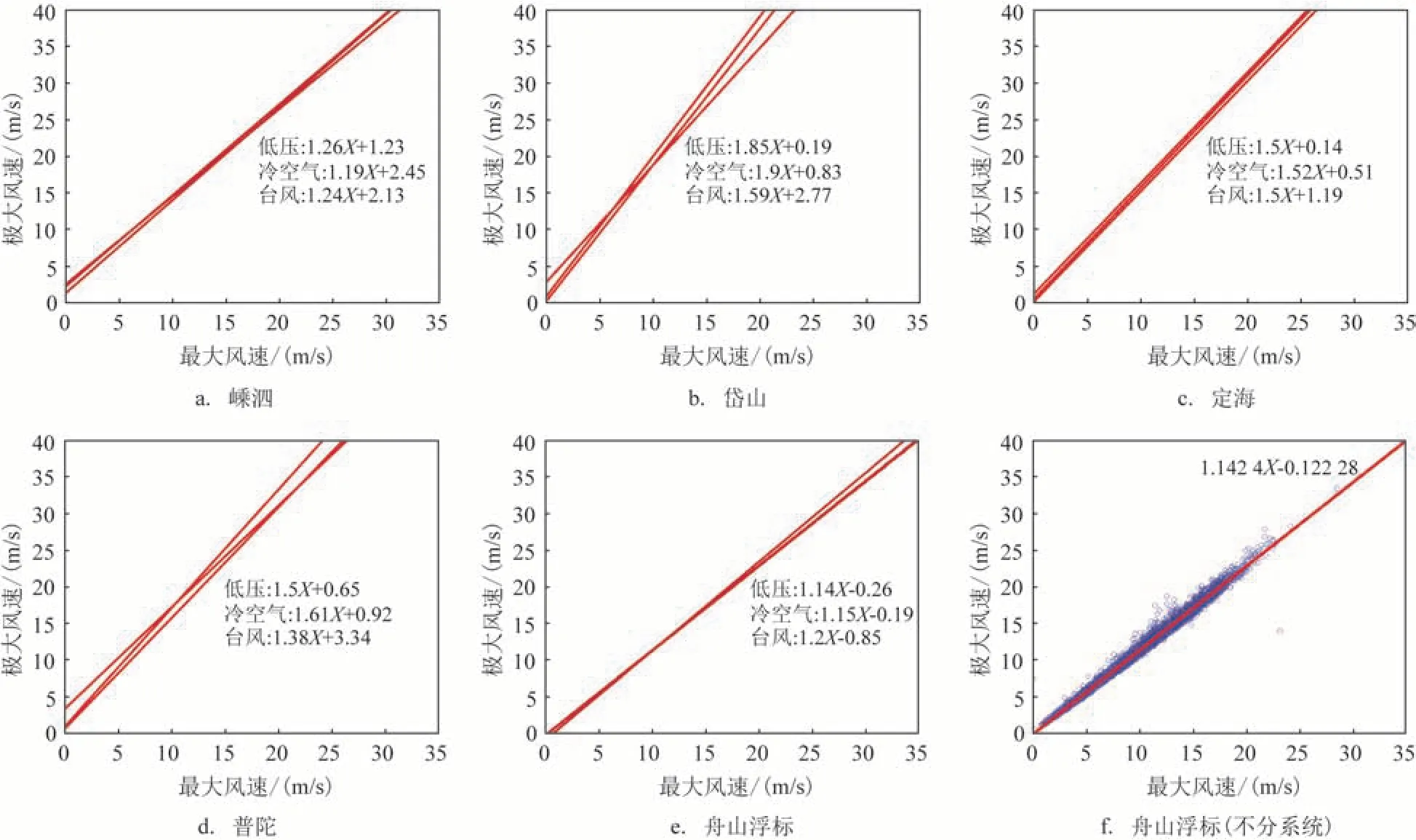
图7 站点分系统最大风速与极大风速关系对比图Fig.7 Comparison diagram of relationship between maximum wind speed and extreme wind speed in station sub-system

4 订正释用效果检验

利用本文订正释用方法，计算各站点各预报时效（0～72 h）逐小时的极大风速平均绝对误差修正率，并与日常业务惯用的人工经验结果进行对比，结果见图8。除个别站点的个别时次外，基于最优训练期的订正释用方法总体修正效果较好，5 个指标站点的修正率分别达到14%、16%、34%、9%、31%。定海和舟山浮标的修正效果最好，72 h 的平均修正率超过30%，其中舟山浮标在各预报时效均有正修正效果，最高达到40%以上，定海除在个别小误差时次修正效果为负外，总体为正，最高达到50%以上；嵊泗基本也为正修正效果；岱山、普陀负修正时次相对较多，但总体仍是正修正效果。

图8 各站点日常业务惯用方法与订正释用方法对比修正率Fig.8 Comparison of correction rate between routine business methods and revised interpretation methods at each site

5 结论

本文介绍了一种基于最优训练期的风力预报小时级订正释用技术，该技术加密细网格风力预报产品至逐小时，选用平均误差最优训练期模型，利用站点最大风速和极大风速的关系进行订正释用。相比实际业务惯用的人工经验，该方法具备一定的改进效果。结论如下：

①以平均误差为模型的最优训练期方法能有效改进ECWMF 模式的风力预报结果。加权误差法、平均误差法在0～15 h 预报时效的改进结果明显优于线性回归法，15 h 后3 种方法的改进效果相差较小。线性回归法对于各预报时效的最优训练期散乱不确定，业务应用效果差；加权误差法对0～5 h、23～72 h 预报时效的最优训练期表现明晰，平均误差法则将明晰范围进一步扩大到0～10 h 和16～72 h预报时效，但两者在11～15 h 预报时效都未给出绝对大概率值，根据概率分布结果，2 h、4 h、10 h分别为11～12 h、13 h、14～15 h 预报时效的最大概率最优训练期。

②最大风速与极大风速的关系总体上以一元线性回归为主，但与地形、下垫面、天气系统等有关。地形致使各风向的风力阵性差异明显，嵊泗、岱山、定海、普陀4个县区本站各风向阵性系数范围分 别 为1.18～1.58、1.40～1.93、1.60～2.15、1.43～1.91，而海上浮标站16 风向阵性系数基本稳定在1.11～1.15；下垫面不同导致风力阵性也不同，4 个县区本站最大风速与极大风速16 风向的平均差分别为2.51 m/s、2.37 m/s、2.37 m/s、2.51 m/s，而舟山浮标站的平均差却仅为0.91 m/s；与陆地沿海站点不同，在开阔的海面上，各天气系统的风力阵性基本一致。

③基于最优训练期的风力预报订正释用方法能有效利用实况数据，将精细风力预报提高至小时级，改进了ECWMF 模式的订正释用效果。对比实际业务人工惯用经验结果，除个别站点的个别时次外，本文使用的订正释用方法总体上修正效果较好，各站点的修正率为9%～34%，其中定海和舟山浮标的修正效果最好，72 h平均修正率超过30%。舟山浮标在0～72 h各预报时效上均有正修正效果，最高超过40%；定海除在个别小误差时次修正效果为负外，总体修正效果为正，最高达到50%以上。