沿空留巷巷旁支护充填加固技术数值模拟研究
张宝君
(山西焦煤山煤国际霍尔辛赫煤业有限责任公司,山西 长治 046600)
随着煤炭开采技术的不断进步,无煤柱沿空留巷技术得到较广泛的应用,该技术不但可以提高煤炭采出率,而且减少回采巷道的掘进量,大大缩短了工作面接替时间,对煤炭实现安全高效开采具有重要的意义[1]。霍尔辛赫煤矿3 号煤层3501工作面开采即采用无煤柱沿空留巷技术。沿空留巷旁支护充填体的稳定性对沿空留巷具有关键的影响作用[2],因此,采用数值模拟方法对巷旁充填体不同参数条件下巷道受力及变形规律进行研究,为沿空留巷的稳定提供理论依据[3]。
1 工程概况
霍尔辛赫矿3501 工作面位于三盘区北部,西部为3502 工作面,北部为未掘巷道,南部为3306工作面,东部为矿井开拓五条大巷及中部风井。3501 工作面煤层平均厚度2.8 m,煤层结构简单,煤层伪顶为炭质泥岩,平均厚度0.9 m,黑灰色,中厚层状,含煤屑,产大量植物化石;直接顶为细砂岩,平均厚度3.2 m 深灰色,厚层状,见白云母,夹细砂质包体,含少量煤屑,见砂纹层理,产有少量植物化石;老顶为砂质泥岩,平均厚度2.4 m,灰色,薄层状,成分以石英为主,长石次之,夹黑色砂、泥质纹线,含煤屑、夹煤线,具斜层理和交错层理,局部具平行层理,分选不好;煤层直接底为砂质泥岩,平均厚度2.2 m,黑灰色,中厚层状,砂质分布不均,见云母,含煤屑,产大量植物化石;老底为中砂岩,平均厚度为10.8 m,深灰色,厚层状,间夹大量黑色泥质纹线。
2 巷旁充填体参数确定
2.1 模型建立
采用UDEC 数值模拟软件建立霍尔辛赫矿3501 工作面数值模拟模型,尺寸为120 m×50 m,底部四周采用位移边界,顶部施加9.7 MPa 上覆岩层均布载荷。根据霍尔辛赫煤矿煤岩层物理力学参数测试结果(引自本矿与中国矿业大学校企合作项目“回采工作面沿空留巷支护工艺优化技术研究报告”),数值计算模型采用的力学参数如表1、表2、表3 所示。

表1 煤岩体力学参数
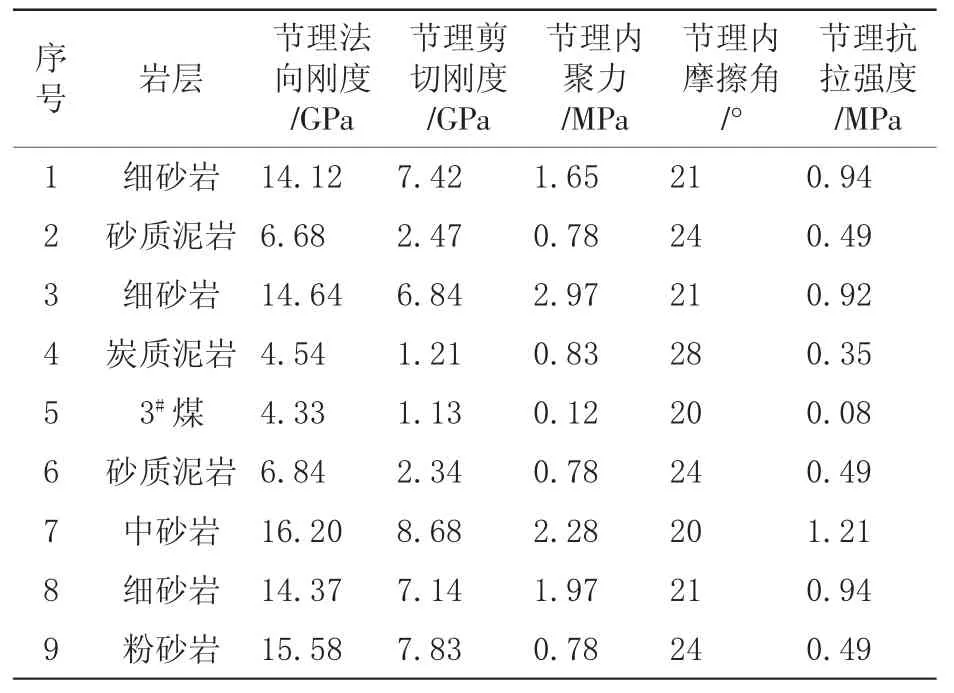
表2 节理力学参数

表3 充填体模拟力学参数
2.2 充填体参数模拟方案
不同充填体参数对巷旁充填体的受力及位移影响也不同,针对充填体重要的三个参数充填体强度、充填体宽度、充填体位置进行组合确定9 个方案如表4 所示。
2.3 充填体数值模拟分析
(1)充填体塑性区分布规律
分析不同充填体参数下得到巷旁充填体塑性区分布特征,可以得到:水灰比相同时,充填体塑性区发育程度随着充填体宽度的增加而减小,充填体宽度相同时,塑性区发育程度随着水灰比的增大而增大;受到矿山压力后,充填体主要发生拉伸破坏,当充填体宽度为1.6 m 时,塑性变形最严重,受到应力最大,此条件下水灰比也最大时,充填体发生较大的破坏。因此,根据充填体塑性破坏规律得到方案3 和方案5 较稳定。
(2)充填体裂隙发育规律
分析不同充填体参数下得到巷旁充填体裂隙发育规律,可以得到:充填体主要产生张拉裂隙,当充填体宽度1.6 m、水灰比为1∶1 时,充填体发生张拉破坏,剪切裂隙数量远少于张拉裂隙;当充填体宽度2.4 m、水灰比1∶1、1.5∶1 时,充填体内部剪切裂隙明显增多。根据充填体裂隙发育规律可以得到,方案5 裂隙发育程度较小。
(3)充填体垂直位移变化规律
分析不同充填体参数下得到垂直位移变化规律,可以得到:不同方案下充填体垂直位移均在充填体中部达到最大;当水灰比相同时,顶底板垂直位移随着充填体宽度的减小而增大,水灰比1∶1时,充填体最大垂直位移300 mm;当充填体宽度相同时,垂直位移随着水灰比增大而增大。根据充填体垂直位移变化规律,方案5 垂直位移较小。
(4)充填体应力分布规律
分析不同充填体参数下水平应力分布规律如图1 所示,可以得到:水平应力均在充填体顶底部达到最大值,而在充填体中部处于应力降低状态;当充填体宽度为2 m、水灰比为1.5∶1 时,水平应力变化幅度较小,充填体相对稳定。
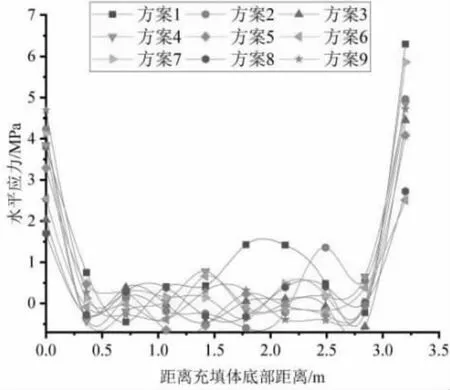
图1 不同方案下水平应力规律
分析不同充填体参数下垂直应力分布规律如图2 所示,可以得到:垂直应力随着水灰比的增大而增大,水灰比为1∶1、宽度为2.4 m 时,垂直应力变化幅度最为明显。
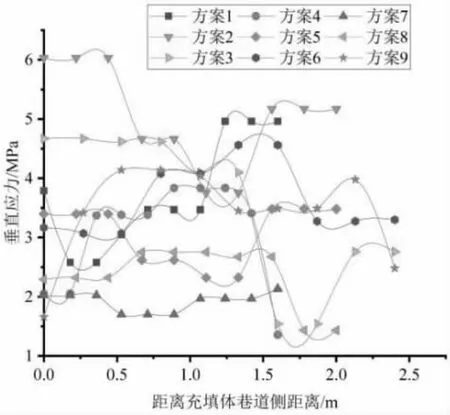
图2 不同方案下垂直应力规律
综上所述,可以得到如下规律: 当水灰比越小、充填体宽度越大时,充填体强度越高,其变形量越小,充填体稳定性越好。对比不同模拟方案下塑性区、应力、变形分布规律,同时结合成本因素,最终确定充填体宽度为2 m,水灰比1.5∶1,将充填体布置于巷道内0.4 m 的支护方案。
3 巷旁充填体加固方案数值模拟分析
在充填体维持自身稳定基础上,通过增加对拉锚杆等加固措施可以对巷旁充填体进行整体加固,形成更高承载力的充填体,因此采用数值模拟方法针对充填体加固技术参数进一步研究。设计充填体加固方案为以下9 个方案,如表5 所示。
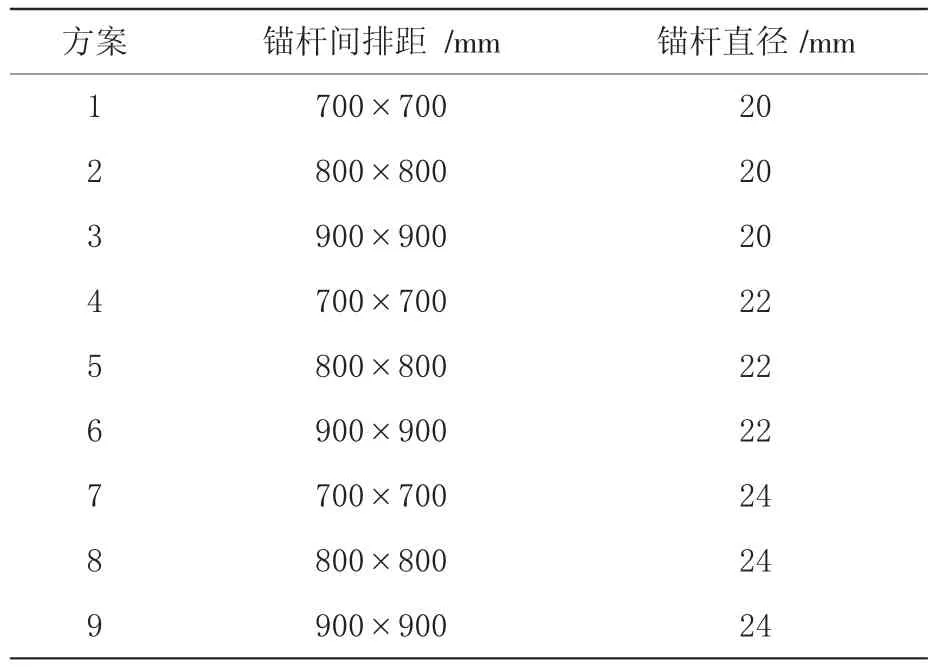
表5 充填体加固技术数值模拟方案
通过分析相关数值模拟结果数据,可以得到如下结论:
1)通过分析不同方案下充填体塑性区分布规律可知,方案7 对拉锚杆直径为24 mm、700 mm×700 mm 时,塑性破坏程度最小;方案4 锚杆直径22 mm、700 mm×700 mm 时,塑性破坏次之,方案5 锚杆直径22 mm、800 mm×800 mm 时,与方案4塑性破坏基本一致,因此方案4、5 均为合理方案。
2)通过分析不同方案下充填体顶板位移规律可知,方案5 与方案7 充填体的加固效果较好;
3)通过分析不同方案下充填体顶板应力分布规律可知,方案5 时,垂直应力变化幅度较小,即锚杆发生剪切破坏可能性较小。
因此,综合三项分析,得到方案5 为最佳充填体加固方案,即锚杆直径为22 mm,间排距为800 mm×800 mm。
4 结论
通过对霍尔辛赫矿3501 工作面沿空留巷充填体支护参数及加固方案数值模拟研究,得出以下结论:
1)通过数值模拟分析了不同充填体技术参数下的充填体受力变形规律,最终确定充填体宽度为2 m,水灰比1.5∶1,将充填体布置于巷道内0.4 m 为最佳支护方案。
2)通过数值模拟分析了不同充填体加固方案下的充填体塑性区分布、应力分布及变形规律,确定加固方案为对拉锚杆直径为22 mm,间排距为800 mm×800 mm。

