两种“合成法”求场强正误的根源

陆小亮

江苏省张家港高级中学，江苏 张家港 215600

1 问题的提出

（2017 年全国III 卷第21 题选择题，改编成了计算题）［1］一匀强电场的方向平行于xOy 平面，平面内a，b，c 三点的位置如图1 所示，三点的电势分别为10 V，17 V，26 V，求电场强度的大小。

图1 电场中的三点

此类题目多次出现在高考试卷中，因此早已形成了解决这类题目的固定解题套路——等分找等势点法：如图2 所示，a 点电势最低，c 点电势最高，因此可以利用等分法在a，c 两点的连线上找到与b 点等电势的d 点，求出d 点坐标为（3.5 cm，6 cm）。连接b，d 两点的直线就是一条等势线，过c 点作等势线的垂线就是一条电场线，垂足为f。根据几何关系可算得c，f 两点的距离Lcf= 3.6 cm，则电场强度的大小为

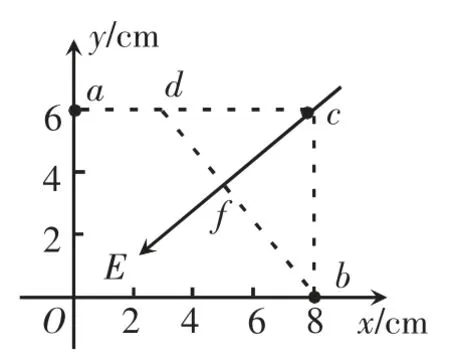
图2 等分法作图

等分找等势点法的物理意义明显，但计算中要使用更多的几何操作过程，尤其是面对空间几何关系复杂的问题时，这种方法的几何操作和运算量很大。因此，近几年在文献［1-3］中另辟蹊径出现了合成法。

1.1 第一种合成法：互相正交的两个方向上的合成法

在c 点合成，如图3 所示，c 点处沿ca 方向和沿cb 方向的分场强分别为

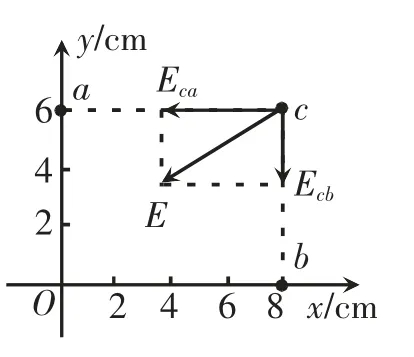
图3 第一种合成法

则合场强大小为

（3）式与（1）式的结果相同。

但这种利用相互正交的两个方向上的分场强的合成法，是否对任意的相互斜交的两个方向上合成也成立呢？ 请看b 点（或a 点）的合成。

1.2 第二种合成法：互相斜交的两个方向上的合成法

在b 点合成，如图4 所示，根据几何关系可知图中θ=53°，b 点处沿ba 方向和沿cb 方向的分场强分别为

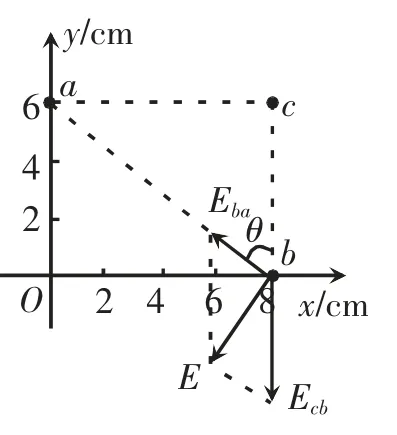
图4 第二种合成法

所以，由余弦定理得，合场强大小为

显然，（5）式的结果与（1）式的结果不同。

问题：b 点处的上述合成法得到的（5）式及其结果为何错了呢？ c 点处合成的结果（3）式与等分找等势点法的结果（1）式一致，是巧合还是必然呢？

2 匀强电场中一个通俗结论的理论分析和推导

电磁学理论中，静电场的电场强度与电势梯度的关系［4］：静电场中某处的电场强度等于该处电势梯度的负值，即若匀强电场在平面内时，此式可写为

对此，可引导高中生做如下分析推导，并归纳总结出一个通俗的结论。

【问题驱动】 匀强电场中，沿与场强方向成θ角的直线上任意两点间的电势差与这两点间距离的比值与场强的关系如何呢？

【分析推导】 场强为E 的匀强电场中，沿与场强方向成θ 角的直线上任取两点A，B，如图5所示。根据高中物理课本中电势差与电场强度的关系“匀强电场中两点间的电势差等于电场强度与这两点沿电场方向的距离的乘积”，则有

【归纳总结】 由图5 和（6）式，引导学生总结出一个通俗的结论：匀强电场中，把场强沿任意两点间的连线和垂直于这个连线正交分解时，沿这条连线方向的分场强等于这两点间的电势差与这两点间距离的比值，另一个分场强与这两点间连线垂直。即两个正交方向上的分场强为：Ex=，合场强为

3 两种“合成法”求场强正误的物理根源

根据上述通俗结论，（2）式确实是匀强电场的场强沿ca 方向和沿cb 方向正交分解后的两个分场强，因此由（3）式合成得到正确的场强是必然的，而不是巧合。

根据上述通俗结论，把真实的合场强E真两次独立地正交分解，即第1 次沿ba 方向和垂直于ba 方向正交分解，所得的两场强分量分别为和E1⊥，第2 次沿cb 方向和垂直于cb 方向正交分解，所得的两场强分量分别为和E2⊥，如图6 所示。显然，图4 中b 点合成时的（4）式，就是在图6 的两次独立的正交分解中，各取一个分场强0.7 V/cm 和用这两个不相关的分场强通过合成法（5）式去求合场强，则是“张冠李戴”，导致错误的结果也是必然的。

图6 两次正交分解

至此，搞清了“第二种合成法：互相斜交的两个方向上的合成法——在b 点合成”错误的物理根源。之后的修正方案，只是一个数学处理和计算的过程，在此不再赘述。