基于马斯京根法的多沙河流输沙演算

杨 飞，刘博伦，江恩慧，王远见，时志晨

（1.黄河水利科学研究院，河南 郑州 450003；2.水利部黄河下游河道与河口治理重点实验室，河南 郑州 450003；3.郑州大学 水利与交通学院，河南 郑州 450001；4.河海大学 港口海岸与近海工程学院，江苏 南京 210098）

0 引言

悬移质输运计算是以黄河为代表的多沙河流的重要研究课题。基于水动力学的河流水沙数值模型是黄河干支流河道最主要的水沙计算工具，但河流水沙数值模型结构复杂、计算量大、定解条件多，不适合大流域水文模型汇总的沟道输沙计算。Li 等［1］将人工神经网络引入河道水沙输运计算，与基于物理过程的水动力模型相比，减少了对地形的依赖。对于黄河这样的大型河道洪水演进中的泥沙计算，目前还缺少快速的水文计算方法。对于一些缺乏实测地形资料的河道，当无法采用水沙数值模型计算输沙过程时，寻找有一定精度的水文方法研究输沙过程显得十分必要。

应用水文模型研究黄河流域产沙输沙时，一般采用水动力学模型或马斯京根水文学方法进行河网汇流计算［2］，多基于恒定流假定进行平衡输沙或不平衡输沙计算［3－4］，与水流采用非恒定计算在理论上是矛盾的。值得注意的是，有相关学者将马斯京根法应用到输沙演算过程中，Choudhury 等［5］以马斯京根法流量演算为基础，依据含沙量与流量之间的单值幂函数经验关系计算含沙量，后来Sil 等［6］根据水沙单值关系，用输沙过程推求流量过程。该方法是在平衡输沙的框架下进行的，严重依赖水沙单值关系，对于含沙量与流量之间不存在一一对应关系的不平衡输沙，计算则不能保证沙量守恒。

为此，本文针对河道输沙过程，以悬沙输运方程和运动波方程相似性为基础，提出一种基于马斯京根水文学方法的泥沙输运计算方法，并以黄河中下游干流河道水沙过程进行验证。

1 马斯京根法输沙率演算

由连续方程和运动方程组成的圣维南方程组，是对河道洪水波的数学描述，连续方程积分可得河段水量平衡方程，动力方程在恒定运动波近似的前提下可得到槽蓄方程［7］，以槽蓄量与示储流量成线性关系的假定为前提的马斯京根流量演算目前已经在黄河干支流河道洪水演算中得到应用。

引入示储流量与河段槽蓄量成单一线性关系的假设，是马斯京根流量演算法的基本出发点。马斯京根流量演算法由河段水量平衡方程［式（1）］和槽蓄方程［式（2）］联立求解，获得河段流量演算公式［式（3）］：

式中：Qu、Qd为河段进口和出口流量，上标n和n＋1 分别表示t时刻和t＋Δt时刻，Δt为计算时段长，W为河段槽蓄量，Q′为示储流量，C0、C1、C2均为流量演算系数，K为蓄量常数（相当于洪水波在河段中的传播时间），x为流量比重因数（主要与洪水波的坦化变形程度有关）。

不考虑惯性项时，运动波方程的空间偏心四点离散求解方法具有马斯京根法的形式，当运动波方程有限差分数值解的误差刚好等于扩散波的物理扩散项时，该数值解即为扩散波方程的精确解［8］，这为该方法的扩散波洪水演算提供了一定的理论支撑。运动波方程的波速为不考虑冲淤与扩散时一维悬沙输运方程为公式形式与运动波方程完全相同，对应的波速为与洪水运动波的波速略有差异，当忽略两者差异时，两者的演进特征一致。因此，理论上适用于洪水运动波和扩散波演算的马斯京根法同样适用于泥沙输运演算。假定不论在输沙率增大阶段还是减小阶段，河段内输沙率是沿程线性变化的，当示储流量与河段槽蓄量成单一关系时，采用与Q′同比重的输沙率Q′S，与该河段水体悬沙槽蓄量WS亦能成单一线性关系，称式（5）为马斯京根法的输沙槽蓄关系式或输沙槽蓄方程，这里输沙的蓄量常数假定和比重因数与水流一致。河段内的泥沙同样满足质量平衡，单位时间内的泥沙质量变化量等于进口与出口输沙率差值加上河道冲淤源项，因此有沙量平衡方程［式（6）］。式（6）和式（5）联立求解获得马斯京根法的输沙率演算公式［式（7）］，本文的输沙率演算思想与Singh 等［9］所建立溃坝洪水演进模型输沙计算方法一致。

式中：QS，u、QS，d为河段进口和出口输沙率，WS为河段水体内悬沙槽蓄量，Q′S为示储输沙率，C0～C3为演算系数，C0～C2与流量演算系数一致，SS为河道冲淤交换源项。

本文建立的流量与输沙率的演算公式，可分段进行演算，即分段马斯京根法。源项根据具体河道的输沙能力与含沙量关系确定，采用不平衡输沙形式时，源项SS为

式中：S、S∗分别为河段平均悬移质泥沙浓度和挟沙力，ω为泥沙颗粒的沉速，α为悬移质泥沙的恢复饱和系数，h为河道断面平均水深，L为河道长度，A为河道断面过流面积。

也可根据实际河段情况采用经验公式计算源项。当不考虑源项时，输沙率与流量的演算公式形式一致。本方法中的水沙传播时间对应了水流与泥沙的运动速度，本文在计算泥沙输运时，采用了与水流相同的传播时间，这意味着本方法假定两者同步传播。当两者传播速度不一致时，导致沙峰滞后于洪峰，需要选择泥沙传播时间进行计算。

2 北干流河道洪水演算

对2018 年汛期和2019 年汛期北干流河段的水沙过程进行演算，选取河曲、府谷、吴堡、龙门、潼关等5个水文站为节点将河曲到潼关河段分为4 段分别演算，以每段上游节点实测水沙过程为输入条件，计算下游节点的水沙过程，其中龙门—潼关段考虑支流汇流过程。北干流河段内有天桥水电站，库容较小，对水流有一定的调节能力，能够改变中小流量的水沙过程，本文没有考虑这部分影响。实测流量过程用于模型参数的率定，实测输沙过程用于模拟验证。龙门—潼关段的流量和含沙量过程计算结果如图1 和图2 所示。

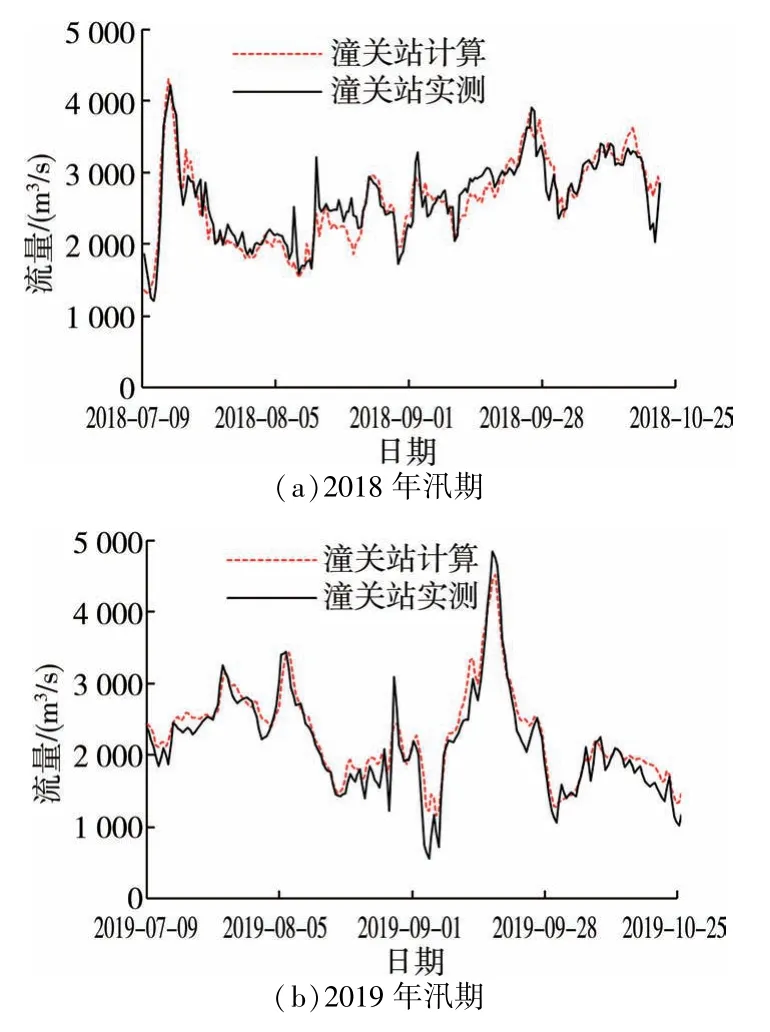
图1 龙门—潼关段流量演算率定结果

北干流河段2018 年汛期和2019 年汛期来水量大，流量演算精度较高，确定系数分别达0.88 和0.90，演算的流量过程与实测过程基本重合。含沙量演算结果和实测结果略有偏差，确定系数分别达0.60和0.78，在不考虑河段冲淤的情况下进行含沙量演算精度是可以接受的，说明所采用的方法可以用于该河段的河道流量与含沙量的演算。

3 黄河下游水沙演算

将所建立的模型用于黄河小浪底至利津河段的水沙演算。在小浪底至花园口河段，考虑伊洛河、沁河入汇，以黑石关、武陟作为支流入口，根据洪水传播时间设定计算时段长为13 h，采用2006 年6 月1 日至2017年汛期实测流量用于率定参数，最小二乘法率定结果的确定系数为0.98，对2018 年汛期至2021 年汛期流量过程验证，整个时段验证结果的确定系数为0.98，图3 为2018 年汛期和2019 年汛期流量过程的验证结果，可以看出，马斯京根法对该河段流量演算的精度较高，演算流量过程与实测过程基本一致。对2006 年汛期至2021 年汛期的输沙率进行验证，确定系数为0.57，图4 为2018 年汛期和2019 年汛期含沙量过程的验证结果，演算的含沙量过程整体上与实际过程拟合较好，总体上看模型可以用于小浪底至花园口河段的河道流量与含沙量演算。小浪底至花园口河段为典型的游荡型河段，洪水期河道冲淤幅度大，输沙调整明显且与含沙量关系密切［10］，导致含沙量较大时演算过程与实测过程偏差较大，为了提高输沙率的演算精度，需进一步在输沙率计算中考虑泥沙冲淤源项。

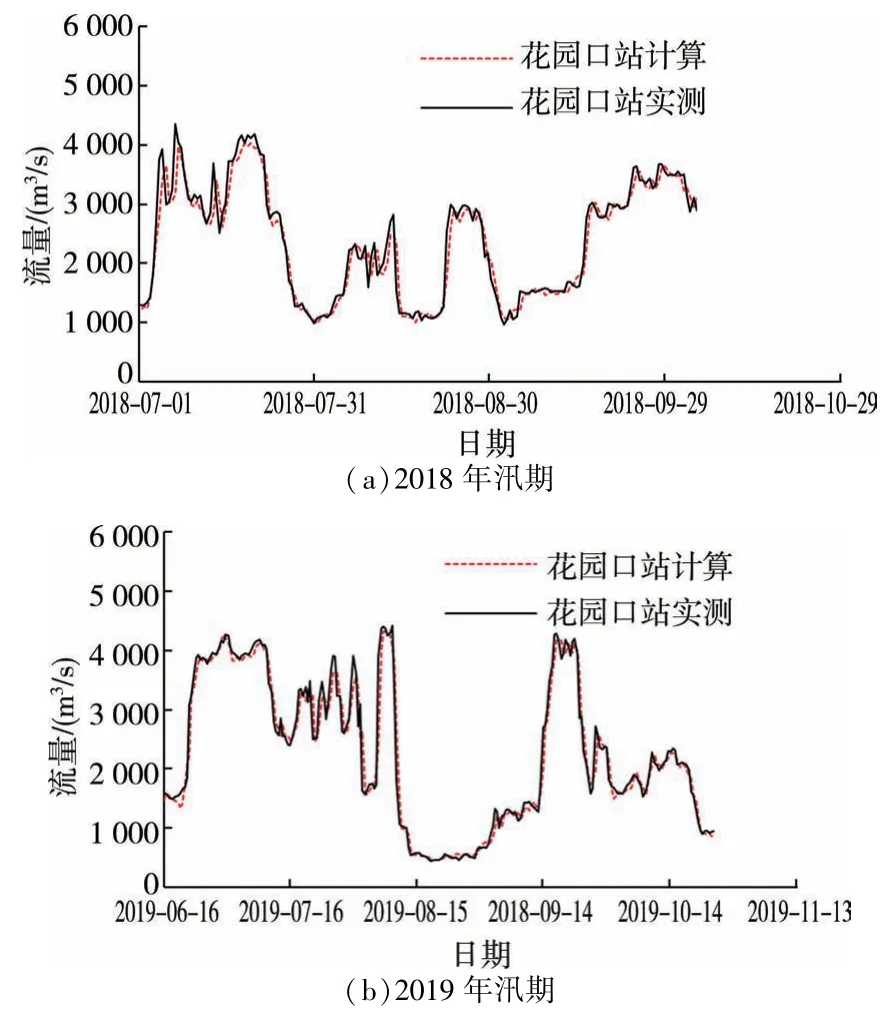
图3 小浪底至花园口河段流量验证结果

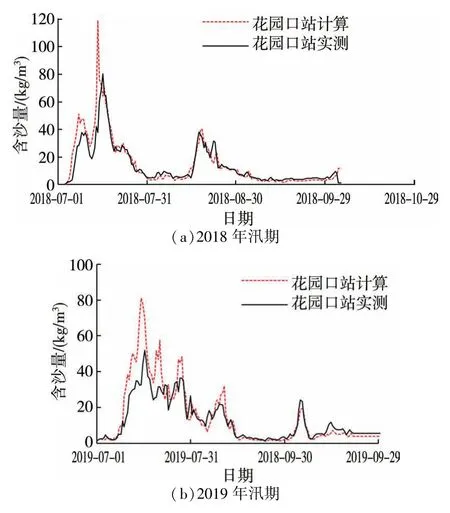
图4 小浪底至花园口河段含沙量验证结果

对于花园口至利津河段，选取花园口、夹河滩、高村、孙口、艾山、泺口、利津等7 个水文站2018 年汛期和2019 年汛期的水沙数据进行分析验证。以7 个水文站为节点将花园口至利津河段分为6 段分别进行洪水演算，不考虑区间内冲淤、引水、支流入汇对水量和沙量的影响，演算下游节点的水沙过程。6 个节点的流量演算精度较高，确定系数均在0.95 以上，这里不再展示。2018 年和2019 年夹河滩站汛期含沙量验证结果如图5 所示，确定系数分别为0.91 和0.84，其他5个节点含沙量验证结果的确定系数均在0.90 以上。可以看出各段的含沙量演算值与实测值非常接近，采用马斯京根方法有很高的精度。受泥沙沿程冲淤变化等影响，泥沙输运的模拟精度略低于流量演算的。

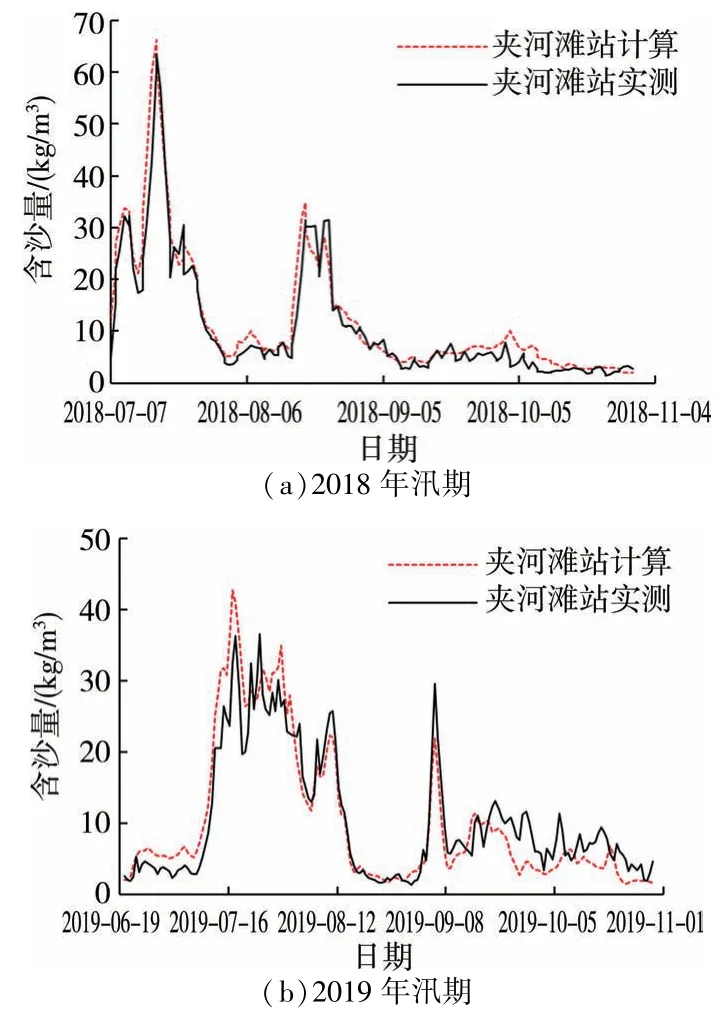
图5 花园口至夹河滩河段含沙量验证结果

4 结论

一维悬沙输运方程和运动波方程的形式一致且波速接近，以运动波方程为理论基础的马斯京根流量演算方法同样适用于悬沙输运演算。据此，本文参照马斯京根流量演算方法，建立了马斯京根法输沙率演算方法。将该方法用于黄河中下游干流水沙过程的演算，结果表明，基于马斯京根法的输沙演算方法能保证一定精度并且计算过程十分简单，可应用在以悬移输沙为主的多沙河流水沙演算。水文预报中当洪水流量过程采用马斯京根法进行演算时，该方法参数能够直接用于洪水输沙预报。

本文所建立的方法高效简单，可用该模型进行大型流域水沙模型中的沟道输沙演算。由于以悬沙为代表的物质输运方程具有普适性，因此所建立的方法对溶质在内的河流物质通量同样适用，其避免了采用水动力学模型的复杂计算，在计算效率上具有优势。