新安江模型参数优化的一种约束SCE-UA算法研究
刘希琛,阚光远,丁留谦,何晓燕,梁 珂
(1.流域水循环模拟与调控国家重点实验室,北京 100038;2.中国水利水电科学研究院,北京 100038;3.水利部防洪抗旱减灾工程技术研究中心,北京 100038;4.水利部京津冀水安全保障重点实验室,北京 100038;5.北京中水科工程集团有限公司,北京 100048)
1 研究背景
概念性水文模型用于模拟天然流域中的复杂水文现象,流域特征通过模型参数进行描述。由于并非所有的模型参数都可由野外观测、实验室测量等途径获取,因此大多数模型参数通常由实测降雨—径流资料反推获得。基于智能优化算法的参数优化方法成为率定水文模型参数的主流方法[1]。
自20世纪二三十年代开始,随着产汇流理论的日趋成熟和计算机技术的逐渐进步,流域水文模型迅速发展[2-4]。迄今为止,新安江模型、TOPMODEL、SWAT、MIKE SHE、HEC-HMS、WEP等模型已广泛应用于流域水文模拟[5-9]。新安江模型是我国应用最广的水文模型[10]。进行新安江模型参数优化时,需要反复运行模型[11],利用优化算法在可行域内寻找较优的模型参数组合,进而获取最优模型参数。传统的优化方法在寻优时,仅考虑模型参数的取值范围,并未考虑模型参数的其他约束条件[12]。以新安江模型为例,无约束条件下的参数优化存在两个问题:一是长历时洪水模拟中,当产流和蒸散发参数设置不当时,易于发生土壤含水量出现负值的现象。以往研究者针对这个问题的常见解决方案是将模拟中出现的负值土壤含水量重置为零,这种处理相当于引入了多余的水量,会导致水量不平衡并降低模拟精度;二是新安江模型的汇流参数CG、CI、CS具有明确的物理意义,他们的大小关系反映了不同水源的汇流速度,但通常的参数优化中并未考虑汇流参数取值的大小关系,可能得出不合理的径流模拟结果。综上所述,在水文模型参数优化中施加约束是十分必要的,需要开展相关研究。
本研究尝试解决新安江模型参数优化过程中的约束条件问题,基于新安江模型原理、参数物理意义和SCE-UA算法,设计了数值模拟实验,探索模型参数组合与土壤含水量正负值之间的关系,在目标函数中构建了罚函数机制,用于处理土壤含水量出现负值的情况,通过罚函数引导参数优化算法寻找非负土壤含水量对应的模型参数组合。汇流参数方面,通过设计罚函数确保汇流参数满足CG≥CI≥CS的大小关系,引导优化算法得到合理的汇流参数组合。数值实验结果表明,提出的约束SCE-UA方法能够使优化算法获得的模型参数更为合理,避免土壤含水量出现负值和汇流参数大小关系错误的不合理现象,能够取得更好的水量平衡效果和更高的模拟精度。
2 考虑约束条件的新安江模型参数优化方法
2.1 新安江模型参数1980年代,赵人俊等提出了三水源新安江模型[13],该模型广泛应用于我国的湿润与半湿润地区洪水模拟与预报工作中[14]。本研究基于三水源新安江模型,按照蓄满产流概念计算降雨产生的总径流量,将径流成分划分为饱和地面径流、壤中水径流和地下水径流。河网汇流采用滞后演算法,河道演进采用马斯京根法。新安江模型需要优化的参数为16个。如表1所示。
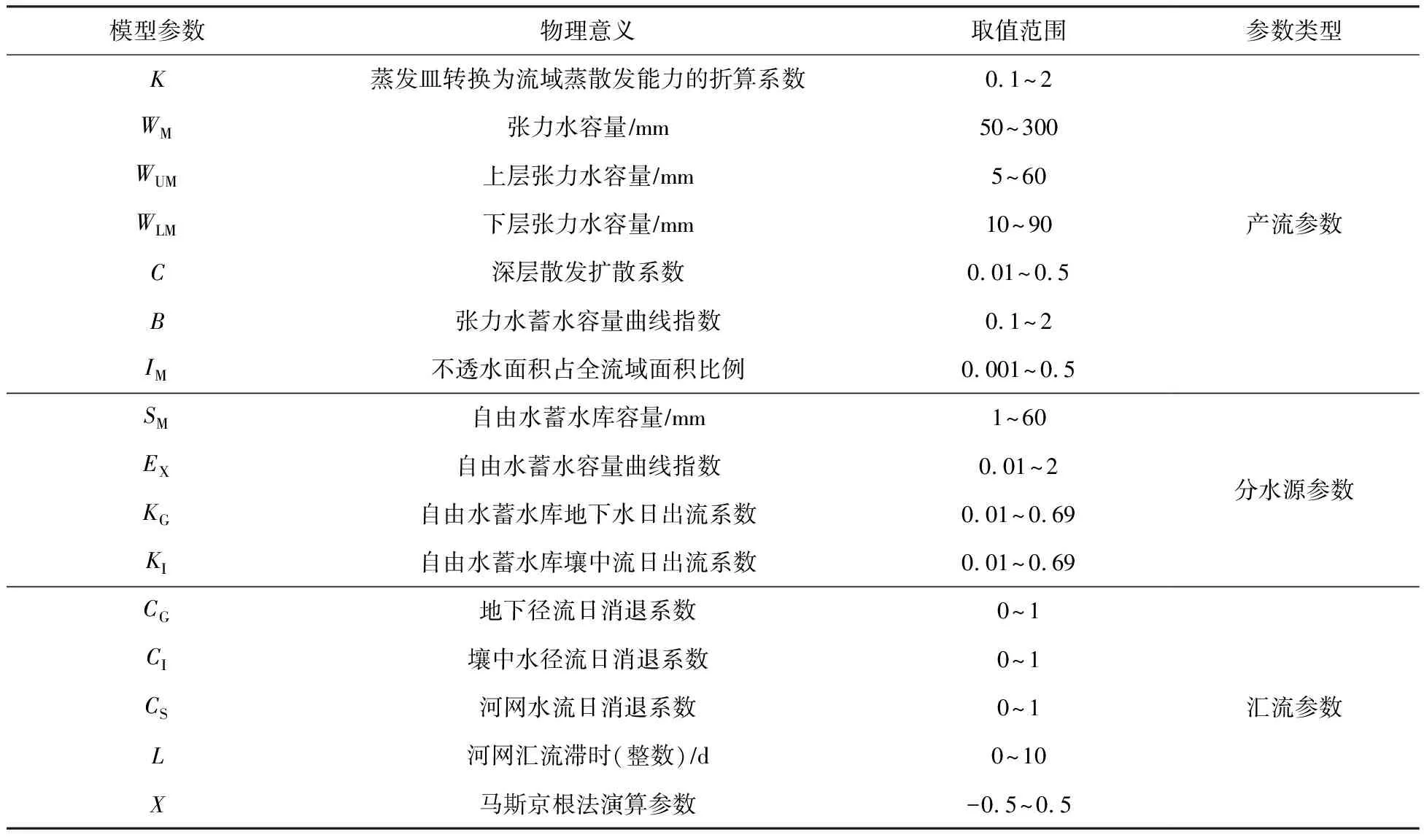
表1 新安江模型参数及其取值范围
本研究选择呈村流域作为研究区域,流域地处亚热带季风气候区,径流年内、年际变化较大,为典型的湿润地区,适用新安江模型。事实上,呈村流域是新安江模型诞生地,模型最初的应用就是从这里开始的,对于本研究来说,呈村流域是较为合适的选择。该流域总面积为298 km2,流域内共有呈村、汪村、左龙、田里等十个雨量站。流域出口水文站为呈村站。由于流域面积较小,可设置各子流域到出口断面的马斯京根分段数为0,因此马斯京根法参数X不参加优化。为了避免参数相关性对参数优化结果的稳定性带来负面影响,引入结构性约束KG+KI= 0.7。最终需要优化的参数个数为14个。
2.2 土壤含水量与模型参数关系分析不合理的参数组合会导致长系列模拟中蒸发过大,进而发生土壤含水量出现负值的现象。土壤含水量是新安江模型产流计算模块的输出,因此,在降雨资料和流域初始状态变量固定的前提下,土壤含水量的计算结果必然与模型的产流参数密切相关。产流参数中,IM的取值相对固定,对土壤含水量影响较小。K反应了流域蒸散发能力,K值越大蒸发越强烈,土壤含水量越小;反之,土壤含水量越大。余下的参数中,WM、B和C相互制约,对土壤含水量的影响较为复杂,故而选择这三个参数作为研究对象。固定其他参数,对WM、B和C进行随机采样并运行新安江模型进行数值模拟,观察土壤含水量是否出现负值。参考其他学者在呈村流域的研究成果[15],新安江模型的参数取值范围见表2所示。

表2 呈村流域新安江模型参数范围
由表1展示了参数的物理意义,WM为流域张力水容量,反映了流域包气带总体厚度,该参数可以分解上层、下层和深层张力水容量,即WUM、WLM和WDM;C为深层蒸散发系数,该值取决于深根植物的覆盖面积;B为张力水蓄水容量曲线指数,该值反映了流域张力水蓄水条件的不均匀性。
采用拉丁超立方体抽样算法[15]对WM、WUM、WLM、C和B进行随机抽样,将抽样结果与其他参数组成样本参数组,将样本参数代入新安江模型并记录模拟结果中土壤含水量是否出现负值(如出现负值,则结果为-1,反之,结果为1),通过观察参数组合的分布探索土壤含水量模拟值的规律。按照以上方法,进行10万次洪水过程随机模拟,参数取值分布与土壤含水量的正负值见下图(其中橙色点据为土壤含水量出现负值的参数组,绿色点据对应土壤含水量始终不出现负值的参数组)。
由图1可知,在降雨资料和流域初始状态变量固定的前提下,WM大于171.16 mm(图中黑线位置)时,模拟结果的土壤含水量就不会出现负值;C越大,则土壤含水量出现负值的可能性越大(即橙色点据越密集),这与C增大导致深层蒸散发量变大加剧土壤蒸发的物理情景相一致;采样结果表明参数B并未体现出明显规律性。三个参数中,WM的规律最为明显:WM越大,土壤含水量出现负值的可能性越小。这一规律可用于指导约束条件罚函数的构建。
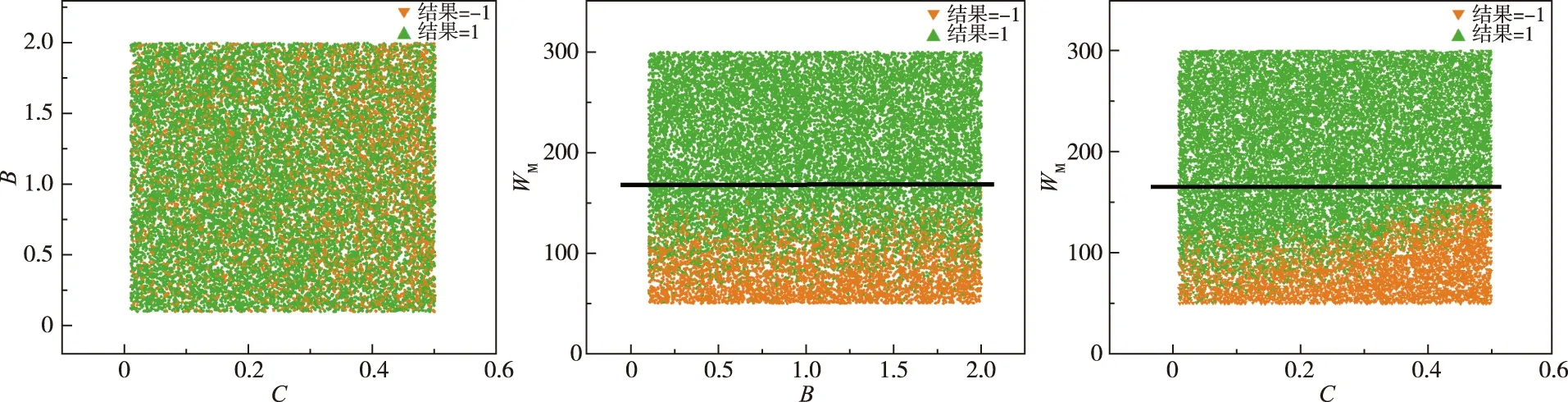
图1 WM、B、C分布与土壤含水量关系Fig.1 Relationship map between WM,B,C distribution and soil water content
2.3 汇流参数物理意义分析CS、CI和CG分别反映了坡面汇流、壤中水径流和地下水径流的汇流速度,且消退系数与汇流速度呈负相关关系[14,16]。同一流域内,坡面汇流速度≥壤中流汇流速度≥地下水汇流速度,因此,我们可以推断,如果汇流参数的取值符合其物理意义,则必须满足约束条件CG≥CI≥CS。这一关系用于设计参数优化过程中模型汇流参数的罚函数。
2.4 约束条件罚函数的构建为了将约束条件应用于模型参数优化,本研究将约束条件以罚函数的形式引入SCE-UA参数优化算法的目标函数中。在参数优化的目标函数计算过程中引入两个罚函数,罚函数实现两种功能:第一,令不符合约束条件的参数样本在种群进化中失去竞争优势;第二,要反映出不合格的参数样本违反约束条件的程度。根据这两项要求,我们设计如下两个罚函数:
(1)保证土壤含水量始终非负的罚函数
如果参数样本计算的土壤含水量出现负值,则目标函数值调整为:
f=λ+λ×(WMmax-WM)
(1)
式中:λ为惩罚因子,取值根据优化目标确定;WMmax为WM的上限,其余参数意义同前。
(2)保证约束条件CG≥CI≥CS的罚函数
如果参数样本不满足CG≥CI≥CS,则目标函数值调整为:
f=λ+λ×(|min(0,CG-CI)|+|min(0,CI-CS)|)
(2)
3 结果及讨论
3.1 径流模拟结果分析本研究通过数值模拟实验,验证参数优化的效果[17]。两组实验均基于研究流域1986—1999年共计14年的日降雨—径流资料,率定新安江模型参数[18]。其中,一组实验采用未引入约束条件的SCE-UA算法;另一组实验采用引入双约束条件的SCE-UA算法(简称约束SCE-UA算法)。每组实验均进行20次参数优化并对结果进行分析。需要注意的是:未引入约束条件的情况下,当遭遇土壤含水量出现负值时将其置零,以确保优化能够连续进行。表3是未引入约束条件的20次优化的统计结果,表4是引入约束条件之后的20次优化的统计结果。
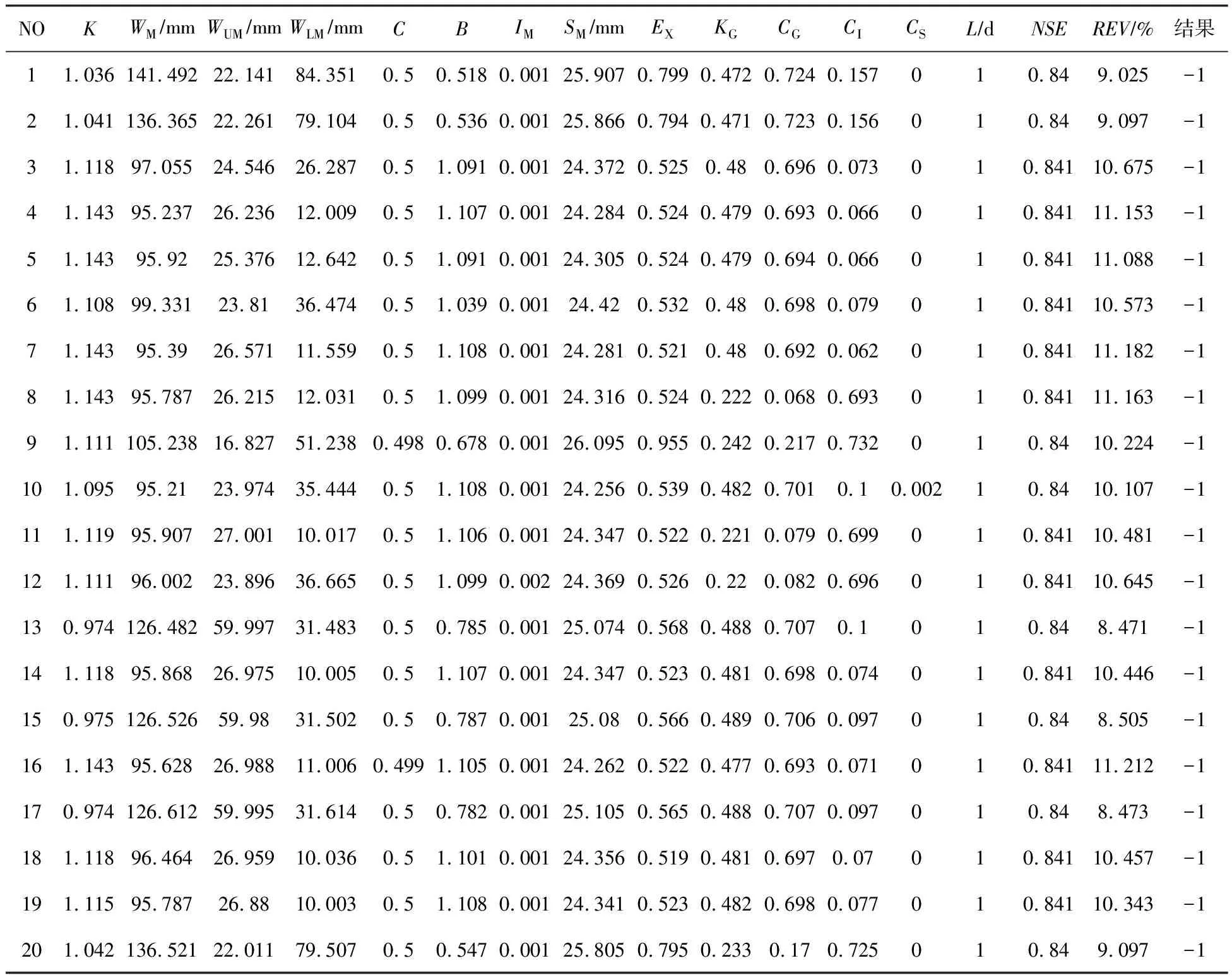
表3 未引入约束条件的SCE-UA算法优化新安江模型参数统计结果
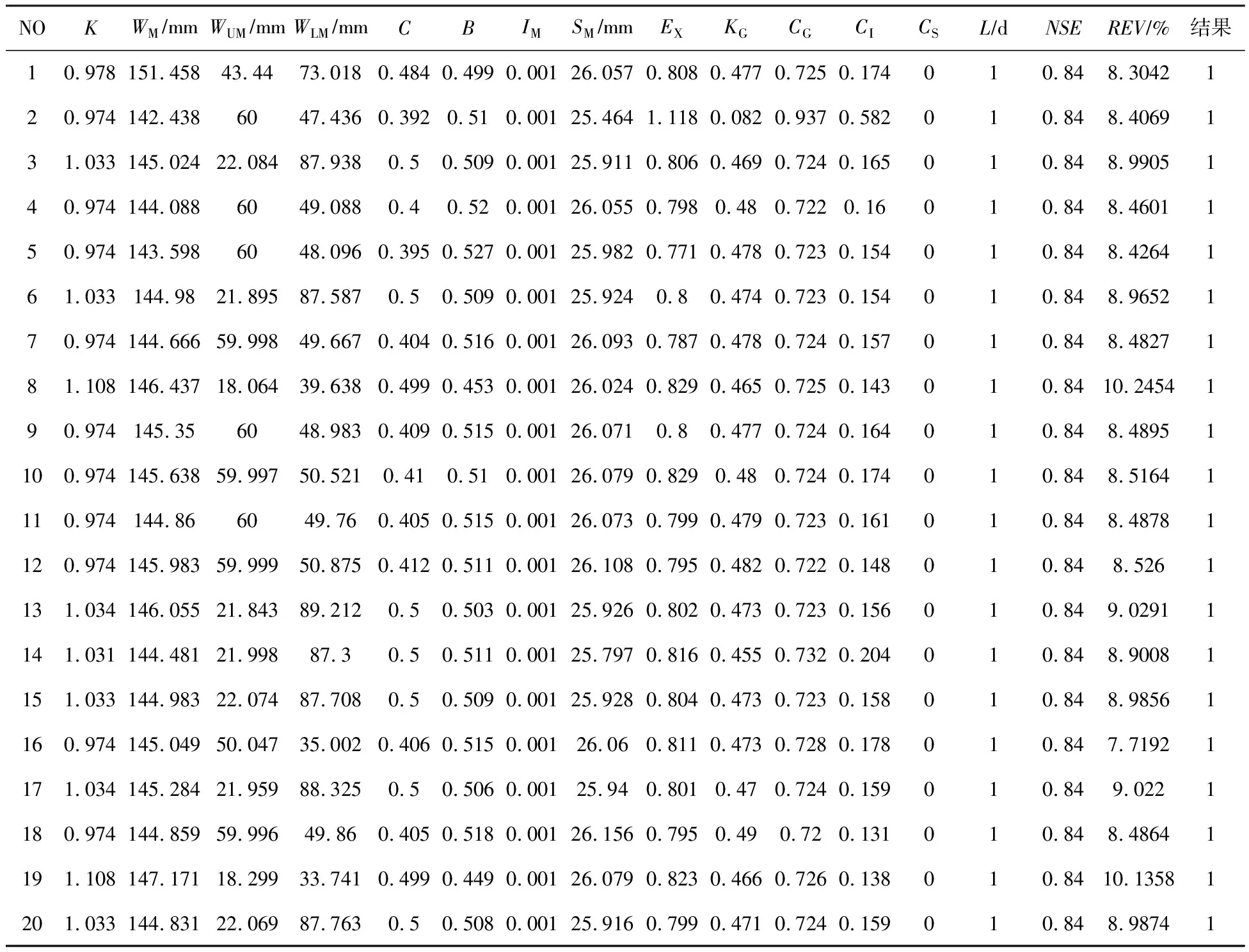
表4 约束SCE-UA算法优化新安江模型参数统计结果
由表3与表4可知,引入约束条件之前,所有的模拟结果中都出现了土壤含水量小于0的情况,且第8、9、11、12、20组参数,出现CI≥CG的现象。引入约束条件之后,模拟结果和汇流参数组合均未出现不满足物理意义的情况。
按照表3与表4设置新安江模型参数值,得到的模拟流量值与实测流量值的散点图如图2与图3所示,(散点图NO.1—NO.20对应着表中模拟洪水NO.1—NO.20),用皮尔森相关系数R来衡量未引入约束条件的SCE-UA算法与约束SCE-UA算法的性能,相关性越高,模拟径流过程精度越高,算法性能越强。
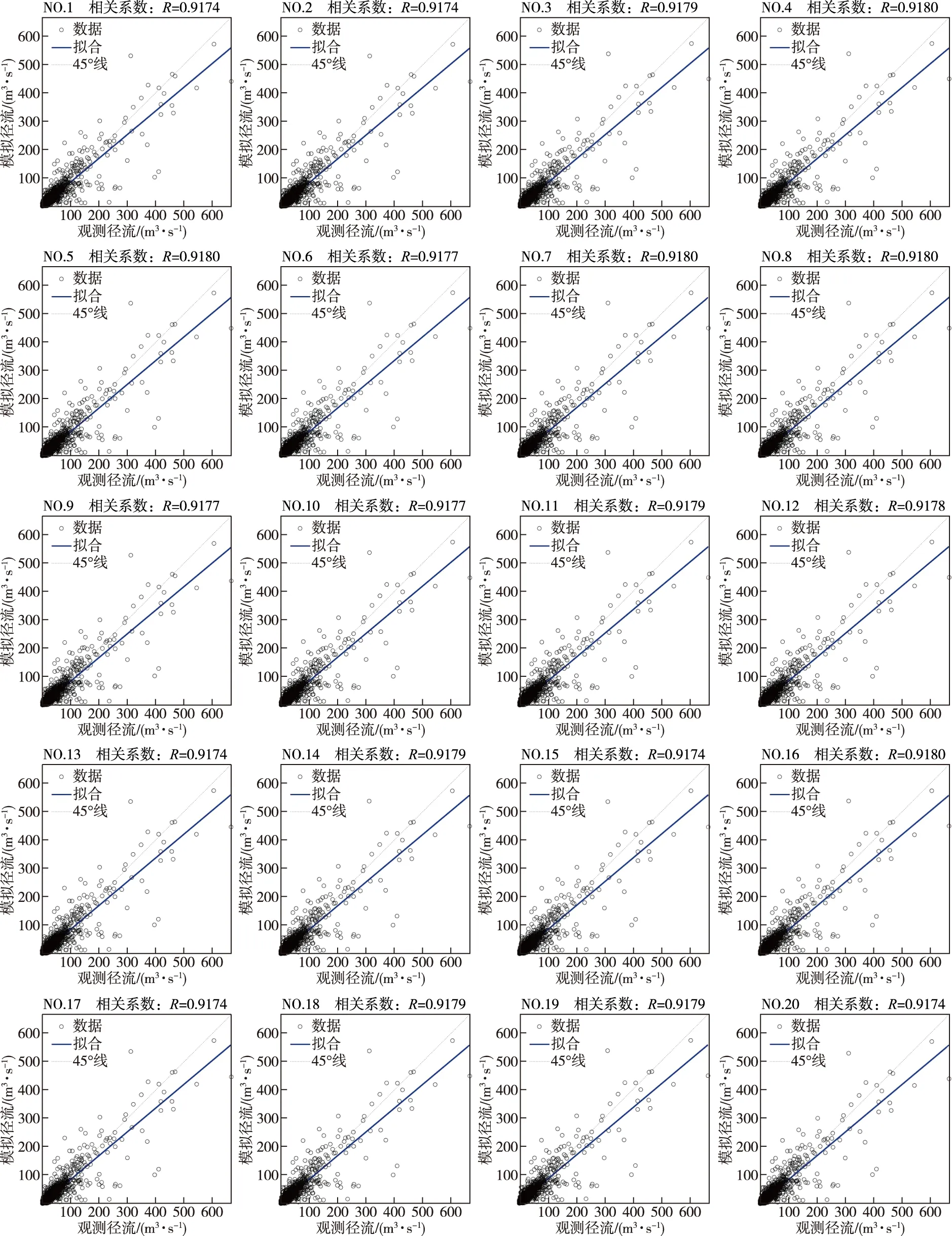
图2 引入约束条件前的水文模拟结果散点图Fig.2 Scatter plot of hydrological simulation results without introducing constraint
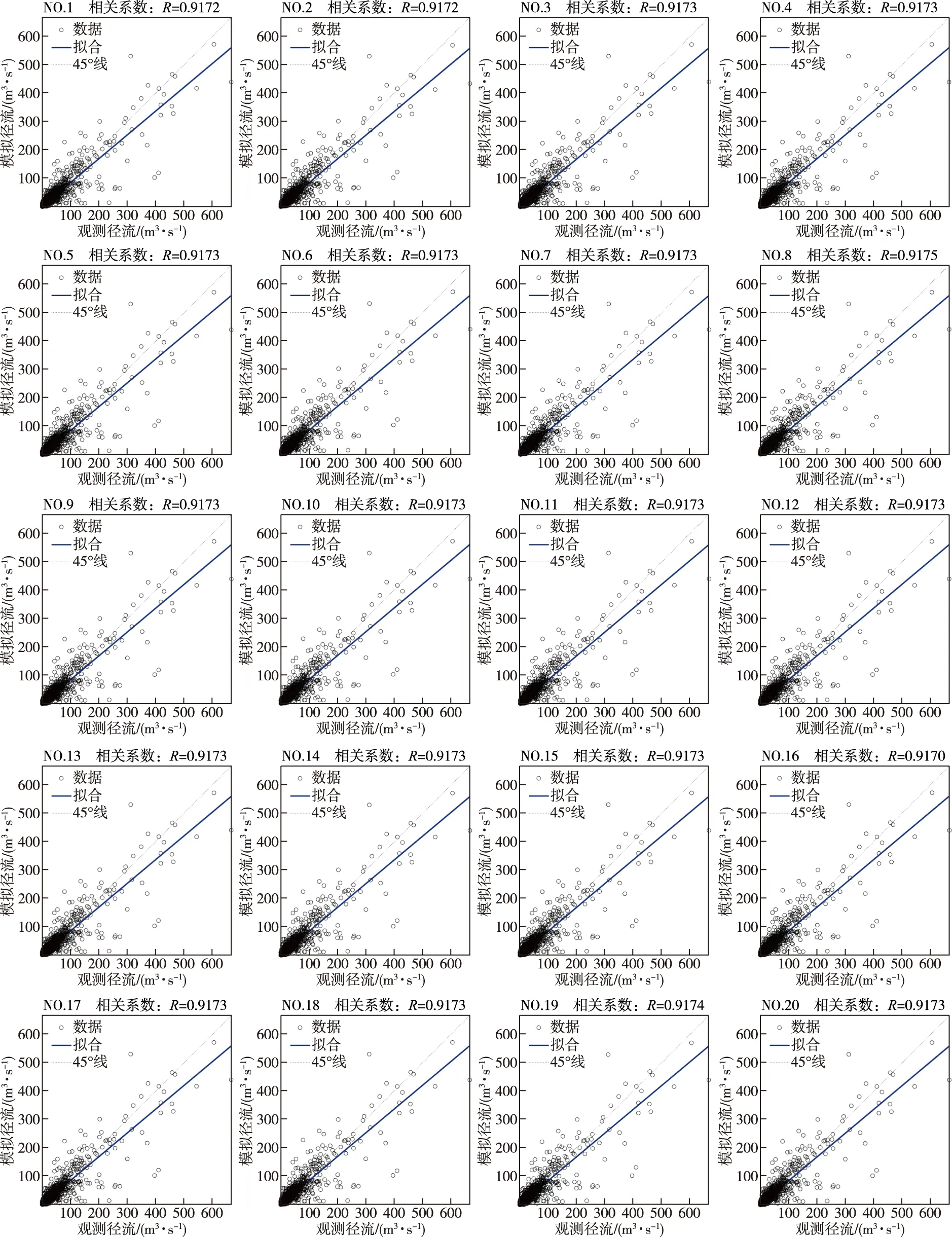
图3 引入约束条件后的水文模拟结果散点图Fig.3 Scatter plot of hydrological simulation results with constraints
图2与图3记录了两种算法的皮尔逊相关系数R,表5统计了模拟径流过程的NSE与R,计算了两者的均值、方差和极差(最大值与最小值之差)。从表5中可知,两种优化算法的NSE均值分别为0.8406和 0.8400(接近《水文情报预报规范》甲级标准),R均值分别为0.9177与0.9173(极强相关),这表明两组模拟径流过程的精度较高且非常接近;两种优化算法的NSE方差与极差、R方差与极差都接近于0,这表明两种算法模拟径流的质量非常稳定,引入约束条件之后,优化结果的可靠性不会受到影响。
综上所述,约束条件不仅可以提供符合物理意义的模型参数集,而且不会降低优化算法的性能,是一种可靠的优化算法。
3.2 算法稳定性分析欧氏距离衡量多维空间中两个点之间的绝对距离,该值越接近于0,说明多维空间中两个点越接近。以某个实验组内所有样本的欧氏距离的均值与方差代表算法的稳定性,其中欧氏距离的均值越小,代表样本间的差异越小;欧氏距离的方差越小,代表样本之间欧氏距离的差异越小。两种算法的欧氏距离的统计值见表6。

表6 两种算法欧氏距离统计值
如表6所示,约束SCE-UA算法欧氏距离的均值和方差都优于SCE-UA算法,这说明约束SCE-UA算法的优化结果之间更加接近,该算法有更优秀的稳定性。
为了进一步论证约束SCE-UA算法在稳定性方面的优势,本文计算了各实验组的参数方差,方差越小,表明算法越稳定。两种优化算法对应的优化结果参数方差见表7。

表7 优化获得的模型参数的方差
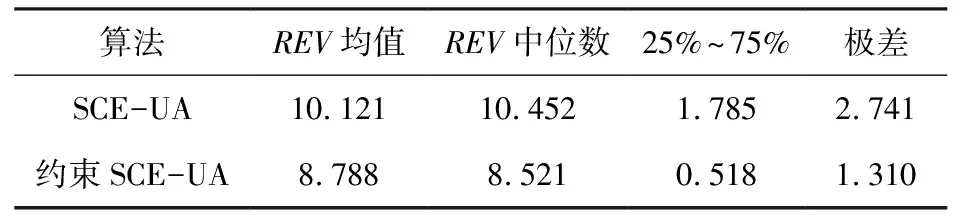
表8 水文模拟结果径流量相对误差统计
由表7可知,除WUM、WDM与C以外,约束SCE-UA 算法的优化结果参数方差均不大于传统SCE-UA算法的优化结果。其中,两种优化算法之间WM方差的差异尤其显著,约束SCE-UA的WM方差仅为传统SCE-UA的1.1%。我们对表 3、表4与表7的结果开展了分析,认为约束 SCE-UA 算法获取的WUM、WDM与C方差偏大现象出现的可能原因如下:新安江模型参数中,WM反映流域包气带总体厚度,该参数在优化过程中可被拆分为WUM、WLM和WDM,分别代表上层、下层和深层的张力水容量。由于模型结构设计的原因,WUM、WLM、WDM和C存在明显的“异参同效”现象,导致了其分布规律较为复杂,这可能是导致方差偏大的诱因之一。此外,本研究统计方差时,样本点个数为 20,这一样本容量相对较小,可能不足以反映所有模型参数分布的规律,这可能是导致方差偏大的诱因之二。
综上所述,约束SCE-UA算法的稳定性要优于SCE-UA算法。造成这种现象的原因是约束条件引导算法在符合物理意义的参数空间进行优化,得到的参数更为合理和稳定。
3.3 径流过程水量平衡分析为进一步验证约束SCE-UA算法在水量平衡方面的优越性,两组实验中均统计了径流量相对误差,引入约束条件前后水文模拟径流量相对误差统计结果如图4所示。
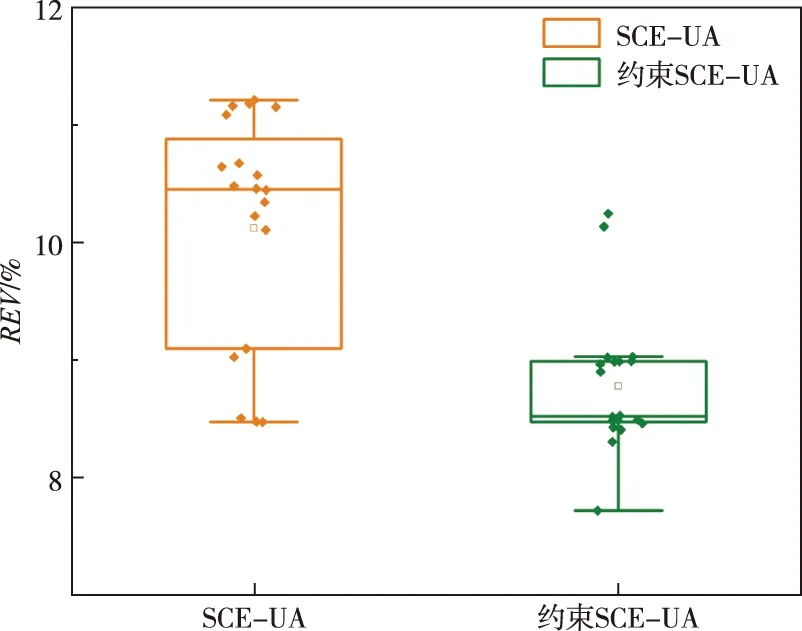
图4 引入约束条件前后水文模拟结果径流量相对误差箱型图Fig.4 Boxplot of relative error of runoff before and after the introduction of constraints for hydrological simulation
由图4可知,约束SCE-UA对应样本的REV中,存在两个异常值,在进行统计时,已将异常值除去。通过图表结果可知,SCE-UA与约束SCE-UA的REV均值分别为10.121和8.788,REV中位数分别为10.452与8.521,约束SCE-UA算法的水文模拟结果径流量相对误差的中位数和平均值明显小于SCE-UA算法的。SCE-UA与约束SCE-UA的REV上下四分位差分别为1.785和0.518,极差分别为2.741和1.310,约束SCE-UA算法的水文模拟结果径流量相对误差的取值更稳定。结果表明,与传统SCE-UA算法
相比,约束SCE-UA算法没有引入额外的水量,能保证水文过程的水量平衡且具有更高的模拟精度。
综上所述,约束SCE-UA算法在保证优化算法性能的同时,不但可以使模型参数和状态变量更符合物理意义,还能保证模拟径流过程的水量平衡,提升径流模拟的精度,是一种更为可靠的参数优化方法。
4 结论
基于以上研究,我们可以得出以下结论:
(1)由数值实验可知,在降雨资料和流域初始状态变量固定的前提下,WM对土壤含水量的正负影响很大,WM越大,土壤含水量出现负值的可能性越小,反之,则土壤含水量出现负值的可能性越大。
(2)本文提出了参数优化过程中的两个约束条件:①土壤含水量始终非负,针对“土壤含水量出现负值”问题,该约束条件提供了一种更好的解决方式,即要求产流参数WM足够大;②汇流参数大小关系始终满足CG≥CI≥CS,该约束条件反映出同一流域内,坡面汇流速度≥壤中流汇流速度≥地下水汇流速度的关系。两种约束条件分别反映了参数优化过程中模拟径流和汇流参数的物理意义。
(3)引入约束条件之后的SCE-UA算法较原SCE-UA算法有以下优点:①水文模拟结果更合理,水量平衡效果更好,两组数值实验的REV统计结果表明,与传统SCE-UA算法相比,约束SCE-UA算法没有引入额外的水量,能保证水文过程的水量平衡且具有更高的模拟精度;②水文模拟过程和汇流参数的物理意义均得到满足,模型参数优化结果不会出现违反物理意义的不合理组合;③优化结果的稳定性更高,两种算法欧氏距离统计结果表明,约束SCE-UA得出的样本之间差异较小,稳定性更强。

