面向车联网多播业务中断概率约束的资源优化研究

王璐

（山西大学 物理电子工程学院，山西 太原 030006）

0 引言

车联网在智能交通系统[1]中应用广泛，例如，在车联网中通过路边单元实时发送交通数据给地面车辆，从而提高城市交通的安全性[2]。然而，在智能交通系统中实时共享高质量实况交通数据仍是一项有待商榷的问题，当有紧急事故发生时车辆无法了解情况可能会造成更加严重的后果。为此，本文提出了车联网中基于单频网络(Single Frequency Network,SFN)技术[3]的交通信息传输方案。

SFN 技术可以同时同频地将数据发送给车辆，有节省频谱资源、信号覆盖范围广等优点，近年来SFN 技术发展得如火如荼，为车联网中数据传输提供了契机。目前关于SFN 多播资源分配的文献，大多是考虑的静态用户。在文献[4]中，作者提出了基于功率的非正交复用技术，采用SFN 技术将数据多播给中心单元用户，实现了地面移动宽带和电视广播系统的融合，从而提高频谱利用率；在文献[5]中，作者对静态用户进行分组，提出一种能够找到接近最优解的算法，从而提高了系统效用；在文献[6]中，作者对静态用户分组，并考虑了视频版本不同对用户观看视频体验的影响，提出了联合优化SFN集群形成、用户分组、视频资源分配和比特率选择的方案，以实现最大化用户的体验质量(Quality of Experience,QoE)；在文献[7]中，作者设计了360°视频直播场景，提出了VRCast 方案，从而提高了用户接收视频的质量，并实现了用户之间的公平性。但上述文献中都是基于用户的瞬时状态，没有考虑用户的移动性，不适用于车联网场景当中，无法准确评估不同时隙车辆的移动位置。

随着5G 技术的愈发成熟和即将到来的6G 时代，自动驾驶、车辆通信[8]等新兴技术高速发展，研究人员对车辆的移动性[9]进行了深入研究，将可以实现快速、高效、合理地进行数据传输，提高接收数据成功率。目前已有文献将重点放在根据车辆移动性进行资源分配。在文献[10]中，作者提出了联合优化任务卸载决策、功率和带宽分配的方案，在降低信噪比(Signal to Noise Ratio,SNR)中断概率的前提下，最小化系统总能耗；在文献[11]中，作者提出了基于多智能体深度强化学习的资源分配框架，在降低SNR 中断概率的前提下，通过联合优化信道分配和功率控制，来提高用户服务质量(Quality of Service,QoS)[12]。上述文献虽然考虑了车辆的移动性，但并未在SFN 场景中考虑在有干扰基站的情况下产生信干噪比(Signal-to-Interference plus Noise Ratio,SINR)中断概率的问题。本文针对车联网中基于SFN 技术的交通信息传输场景，提出了资源分配方案来降低SINR 中断概率，最小化SFN 中每个路边单元(Road Side Unit,RSU)的传输功率。

综上所述，本文主要贡献有：(1) 采用了SFN 技术将数据同时同频发送给车辆，同时考虑车辆移动性，传统的系统模型中只考虑静态用户，本文模型在构建MDP时，考虑了车辆实时移动位置坐标、行驶速度等，基于动态的信道信息来优化RSU 的功率分配；(2) 传统的SFN传输方案中并没有考虑干扰基站对传输功率的影响，本文在SFN 场景中考虑在有干扰基站的情况下产生SINR中断概率的问题；(3)采用基于好奇心驱动的 DQN(CDQN)资源优化算法来求解，与其他强化学习算法相比，该算法收敛速度更快，收敛值更高。

1 系统架构

1.1 系统模型

本文设计了基于车联网的实时交通信息传输场景。如图1 所示，路边部署了3 个路边单元(Road Side Unit,RSU)，道路上行驶的车辆通过无线信道与RSU 可靠地通信，这些RSU 所在区域构成了一个SFN 区域，在事故发生路段，SFN 服务于即将路过事故发生路段的车辆集合，确保集合中每个车辆都能可靠地接收到信息，从而保证司机与乘客的安全。RSU 由多单元协调实体(Multicast Coordination Entity,MCE)来控制，MCE对其覆盖范围内的所有车辆做出功率分配决策。SFN 中的每个RSU 都配备了一个具有高度定向波束的天线阵列。假设主瓣的波束宽度仅足以覆盖目标车辆集合，主瓣的增益为GT,v，旁瓣的增益为零。干扰基站配备有各向同性天线，传输增益为GI,v。令I={0,1,2,…,I}表示RSU 集合，V={0,1,2,…,V}表示车辆集合，J={0,1,2,…,J}表示干扰基站的集合。

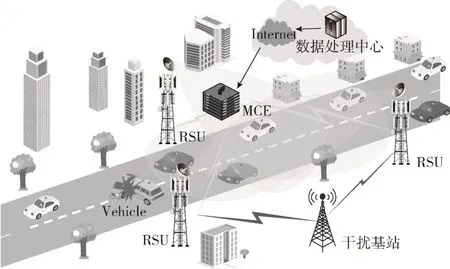
图1 系统模型

假设目标车辆集合中每个车辆通过最近的RSU 定期可靠地将其位置发送到MCE。因此，MCE 可以准确地估计目标车辆集合中所有车辆的几何中心。SFN 覆盖范围内的每个车辆都配备了具有接收增益GR的各向同性天线。SFN 中的RSU 在传输交通信息时会受到周围干扰基站的影响。

本文假设场景中干扰基站服从二维齐次泊松点过程(Poisson Point Process,PPP)Ψ，其中强度为λI，如图2所示。路边基础设施(RSU 和干扰基站)与目标车辆集合中心之间的链路有视距(LoS)和非视距(NLoS)两种状态。假设干扰基站与目标车辆集合中心处于LoS 状态的概率为pLoS，处于NLoS 状态的概率为pNLoS=1 -pLoS。利用PPP[13]的独立细化定理，可以得出LoS 干扰基站ΨL⊆Ψ和NLoS 基站ΨN⊆Ψ的PPP 是相互独立的，密度分别为λI,LoS=pLoSλI和λI,NLoS=pNLoSλI，此外ΨLoS∩ΨNLoS=∅也成立。假设SFN 中的RSU 与目标车辆集合中心始终处于LoS 状态。将第i个RSU 与目标车辆集合中心之间的距离表示为dT,i。同样，第j个干扰基站与目标车辆集合中心之间的距离为dI,j，这是MCE 已知的。如果干扰基站j与目标车辆集合中心处于LoS 状态，则lj,LoS=1，否则lj,LoS=0。第j个干扰基站的路径损耗η(I)(dI,j)定义如下：

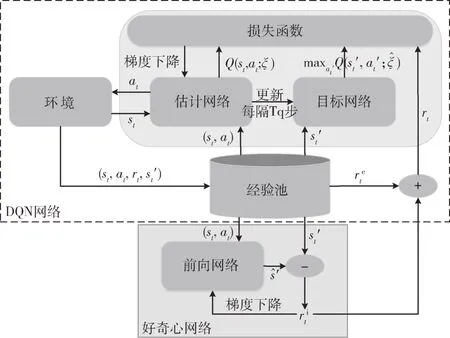
图2 C-DQN 算法

其中，αLoS和αNLoS分别为LoS 和NLoS 状态下的路径损失指数。由第i个RSU 发送，目标车辆集合中心接收信号的路径损耗为η(T)(dT,i)=

假设干扰服从PPP，本文利用Slivnyak 定理[13]，目标车辆集合中心的起始坐标原点为O=(0,0)。因此，SINR表示为：

其中，Pi为SFN中第i个RSU的瞬时传输功率；hi是由基站i(SFN 或干扰基站)引起的小尺度衰落系数，本文采用瑞利信道模型，hi遵循一个均值等于1 的指数分布；W表示热噪声功率。

为保证信息成功传输应降低SINR 中断概率，其中影响SINR 中断概率的主要参数为瞬时传输功率。因此转向推导SINR 中断概率的封闭表达式，它是优化每个Pi的基础。

1.2 SINR 中断和速率中断概率分析

为了提供一个描述SINR 中断和速率中断概率的解析模型，本文证明了以下命题。

命 题1：设I=为目标车辆集合中心的干扰功率。I的拉普拉斯变换为：

其中，LI,Y(s)是由LoS基站(Y=LoS)或NLoS基站(Y=NLoS)产生的干扰功率的拉普拉斯变换，对于αY≥2，定义如下[13]：

证明：在LI,Y(s)[13]中，ΨLoS和ΨNLoS是独立的PPP，由LoS 基站产生的干扰在统计上独立于由NLoS 基站产生的干扰，因此式(3)成立。

定 理1：设μi=,∀i=1,…,M。考虑集合K={μ1,…,μM}，并将C={μ1,…,μa}定义为由 与K 中相同的元素组成，但没有重复元素的集合。此外，本文将ol定义为K中μl的重复次数，其中l=1,…,a。设Pe(β)为相对于阈值β的SINR 中断概率，即SINRO小于阈值β的概率，将Pe(β)表示为：

证明：根据式(2)，Pe(β)可以表示为：

其中，x≥0。

根据式(9)，将式(8)重新改写为：

其中，LR(y)可以根据I0的拉普拉斯变换表示如下：

其中，将Nl具体表示为：

证明：对于l=1,…,M，在式(5)中，令a=M,ol=1 来进行证明。

引理1：当干扰基站网络的半径趋于无穷大[13]时，定理1 和推论1 成立。当半径有限时，Pe(β)值的上限为式(5)或式(13)的等号右边数值。

根据定理1 可以推导出速率中断概率公式，即当系统的可达速率小于传输速率时，则视为通信发生中断。

定理2：当目标速率值为γ时，速率中断概率函数表示为：

其中，ω为系统带宽，而参数S和Z为由调制和编码方案决定的速率校正因子[15]。

证明：根据香农定理，传输速率表达式为S·ωlog2(1 +Z· SINR)。根据文献[16]中定理1 和本文定理1，可以将R(γ)表示如下：

这句话很轻，但仍然在人群里起了作用。大家都不说话了，似乎都在为驮子感到可怜。这时，大家又听见常爱兰一边笑着，一边大声地说，有空你们到我们江西来玩噢，有空一定要来噢。

因此，式(15)成立。

1.3 优化问题建模

利用定理1，本文优化了SFN 中每个RSU 的传输功率，以下是功率分配问题。

该模型的目标函数由SFN 中每个RSU 的传输功率之和给出，本文目标是最小化目标函数。式(17a)表示SINR 中断概率小于或等于目标值H∈[0,1]，其中β̂为目标SINR 阈值；式(17b)表示每个RSU 传输功率的约束条件。

由于车辆移动位置和传输功率具有马尔可夫性[17]，因此在本节中，上述优化问题被建模为马尔可夫决策过程MDP。MDP 由＜S,A,P,r＞组成：S表示状态空间，其中包含RSU 与车辆m之间的距离dT,i；A表示动作空间，其中包含资源分配策略；P表示状态转移概率。由于很难对P进行预测，因此本文采用了无模型的DRL 方法来处理上述的MDP 问题，r表示执行完一个动作后，环境反馈给智能体的回报大小。

2 基于C-DQN 算法的资源优化

传统的强化学习(RL)算法大多缺乏探索能力[18]。为了使智能体更有效地探索，本文提出了基于C-DQN算法的资源分配方案来解决优化问题(17)。

2.1 好奇心驱动的C-DQN

图2 为提出的C-DQN 算法的框架，其中C-DQN 算法包含了两部分：一部分为传统的DQN 算法部分，该部分输出基于训练的状态动作值函数Q(st,at)；另一部分为好奇心网络模块，该网络输出好奇心驱动的内在奖励信号。在每个学习步骤中，智能体在状态st下采取行动at，获得奖励rt，该奖励不同于传统DQN 算法反馈给智能体的奖励，它包括内生刺激产生的奖励和外部奖励两部分，其中外部奖励表示为：

通过从经验池M[19]中提取样本来最小化损失函数：

其中，Q(st,at;ξ)表示参数为ξ的估计网络的状态网络动作值函数，y为目标值，表示为：

其中，rt=，γ∈[0,1]为折扣因子，Q̂表示参数为ξ̂的目标网络（由ξ̂=ξ更新）的状态动作值函数。参数ξ沿损失函数(21)的随机梯度下降方向进行更新，即：

其中，0 ≤αq≤1 为DQN 算法中的学习率。

2.2 基于C-DQN 的资源优化算法

在原始的好奇心模型[20]当中，包含了前向模型和反向模型，反向模型的作用是预测智能体执行的动作(从当前状态st转移到下一状态)，但在本文模型中，状态空间中已经剔除了与智能体无关的状态，仅包含对智能体有影响的状态，因此本文仅保留了前向模型。如图2 所示，好奇心网络作为一个内在奖励生成器，由前向模型和生成内在奖励的减法器组成。在好奇心网络中通过从经验池中提取样本(st,at,)来训练前向模型，该模型通过对下一状态进行预测，将状态预测值与下一状态实际状态值进行比较，从而得到内在奖励。

从经验池中选取at和st，先将原始状态st编码为特征向量ϕ(st)，再利用前向模型对这两个输入进行预测，得到含参数为η的下一状态的预测值：

损失函数为：

好奇心驱动模块通过最小化损失函数来更新前向模型的参数η，该策略表示为：

其中，αc为好奇心驱动模块的学习率。前向模型的预测误差作为好奇心的衡量标准，被定义为在研究中由好奇心驱动的内在奖励，将其表示为：

其中，τ＞0 为缩放因子。用来衡量智能体对当前环境的好奇程度，鼓励智能体驱动好奇心来更有效地探索环境，当值越高，表明智能体对当前环境好奇心越大，刺激智能体去探索环境；反之，当值越低，则表明当前智能体已对环境有了充分的认识。

基于C-DQN 的资源优化算法整体流程为：(1)初始化DQN 网络和好奇心网络的参数；(2)将存储数据(at、st、rt以及)存放在经验池M中；(3)抽取经验池M中的数据来训练DNN，得到最优策略(资源分配策略和视频版本选择策略)。

3 仿真结果与讨论

仿真的硬件配置为笔记本电脑，CPU 版本为i7-6500U，运行内存大小为8 GB，仿真软件使用的是Python 仿真器，采用TensorFlow1.4.0 版本，环境中构造的场景是一条城市公路上部署3 个RSU 和多个(5 辆～50 辆)行驶的车辆。

图3 是不同学习率的收敛性能，通过反复实验来进行设置，在图中较深的线表示平均值，阴影区域表示平均值±标准误差，这反映了曲线的方差。从图中可以看出，当αq=0.003时，相比αq=0.000 1 时远远超过其收敛速度，αq=0.003 时在图中50 回合左右就达到收敛，但是αq=0.000 1 时在100 回合左右才达到收敛。当αq=0.015时，虽然和αq=0.003 时的收敛速度基本一致，但是αq=0.015 时收敛后整体奖励值低于αq=0.003 时的奖励值，因此当学习率为0.003 时学习效果最佳，并将学习率固定为αq=0.003。

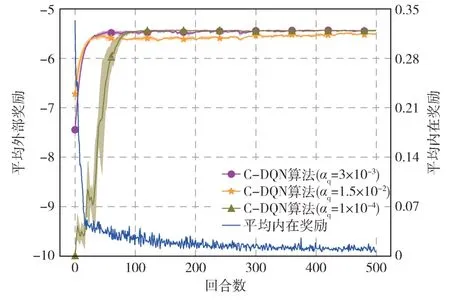
图3 不同学习率

图4 中显示了所提算法与DQN 算法和Double DQN(DDQN)算法的收敛性能比较，图中横轴表示回合的数量，纵轴表示每个回合积累的平均外部奖励。由于内在奖励仅用于提高智能体的自身探索能力，因此不包括在算法比较中。从图中可以看出，所提算法在50 回合左右达到收敛，而DDQN 算法在100 回合左右才达到收敛，且DDQN 算法的波动性明显高于所提算法的波动性。DQN 算法整体平均奖励低于所提算法奖励值。

图4 本文算法与其他算法性能比较

图5 表示的是RSU 的不同传输功率所占比例。本文优化目标是最小化SFN 中每个RSU 的传输功率之和，限制条件是SINR 的中断概率不超过目标值H，从公式中可以看出，要满足中断概率不超过H的要求，当H越来越小，对应分配RSU 的传输功率要越来越大，因此该限制条件是与优化目标是相互制约的，从图中可以看出，随着H的逐渐减小，对应分配的功率不再一味地追求最小功率，对应的大功率所占比例随着H的减小，比例逐渐增大。

图5 不同SFN 传输功率

4 结论

本文提出了车联网中基于SFN 的实时交通数据传输方案，通过资源分配来实现最小化SFN 中RSU 的传输功率，上述优化问题被建模为MDP，并采用C-DQN 算法来解决该问题。利用Python 软件对本文模型进行仿真，反复调整算法参数从而实现最佳收敛，验证了算法的有效性，同时本文的C-DQN 算法与DQN 算法和DDQN 算法性能相比，在好奇心的驱动下有显著的探索能力，收敛速度和奖励值都高于上述两个算法。