Fair multigroup multicast precoding design based on traffic demands for multibeam satellite systems

Zhiqi DAI, Zhen XU

School of Electronic and Information Engineering, Beihang University, Beijing 100191, China

KEYWORDS

Abstract Onboard resources are limited for multibeam satellite communication systems,while differences exist in traffic demands among users.Since conventional multigroup multicast precoding methods do not take traffic demands for users into consideration, it is difficult to flexibly adjust the offered throughput to users’demands.Users with higher demand may obtain lower throughput while users with lower demand may be over-satisfied, which results in the requested-offered throughput mismatch and resource waste.This paper proposes a fair multigroup multicast precoding design based on traffic demands.To obtain the precoding design, the optimization problem aimed at maximizing the minimum throughput satisfaction ratio, which is defined as the ratio of the offered throughput to the traffic demand,is formulated,so as to provide fair service for all users while satisfying per-feed power constraints and traffic demand constraints.To address this problem,an auxiliary variable is first introduced to equivalently simplify it.Then,the semidefinite relaxation and the bisection search strategies are adopted to further handle the problem.Finally, the optimal precoding vectors are obtained by employing eigenvalue decomposition or Gaussian randomization.Simulation results indicate the effectiveness of the proposed precoding algorithm and demonstrate that it can better adapt to the scenarios with different traffic demands.

1.Introduction

Satellite communication, supported by its unique merits of wide coverage as well as independence of geographical conditions and land disasters,1–3is an effective solution to compensate for deficiencies of terrestrial communication systems, and will therefore play an indispensable role in future communication systems by providing ubiquitous connectivity.4,5The growing interest in the emerging applications such as interactive multimedia services calls for the development of the satellite communication systems capable of providing higher throughput to accommodate the ever-increasing data rate demands.This leads to the evolution of satellite systems from single-beam to multibeam architectures.6,7Frequency reuse among beams can be adopted to improve spectrum utilization and achieve better performance in multibeam satellite systems.To support the terabit capacity, multibeam satellite systems with full frequency reuse have become the trend for the next generation satellite communications.8However,aggressive full frequency reuse may result in severe Inter-Beam Interference(IBI).9Recently, precoding, which preprocesses transmit signals at the Gateway (GW), has attracted extensive interests and attention because it can significantly mitigate multibeam interference to improve throughput.6,8–10In the existing satellite communication standards such as DVB-S211and DVBS2X12, the data of multiple users in a group are encapsulated in the same frame, which makes each beam of the satellite serve multiple users simultaneously.13In such multicast transmission, multiple users served by a beam share the same precoding vector.14Our study focuses on multigroup multicast precoding for multibeam satellite systems to reduce IBI.

In the literature of precoding for multicast multibeam transmissions, the design that extends the Minimum Mean Square Error (MMSE) algorithm from unicast to multicast by means of channel averaging is presented in Ref.15, which is the first attempt to design multigroup multicast precoding for satellite communications.This simple approximation that equates all users within the same frame to a single user improves spectral efficiency, but the performance degrades increasingly as the number of users per frame increases.Furthermore, in order to improve the performance, the precoding design can be modeled as a multigroup multicast optimization problem.In Ref.14, the problem of frame-based precoding for multicast multibeam satellite systems is proposed, aiming at maximizing the sum rate under per-antenna power constraints,and the problem is solved via a heuristic algorithm based on joint precoding and power allocation.Joroughi,et al.16design a two-stage low-complexity precoding scheme to deal with the multiuser interference for multibeam multicast satellites, in which the inter-beam interference is minimized in the first stage, while the intra-beam Signal-to-Noise-plus-Interference Ratio (SINR) is enhanced in the second stage.However, in an actual multibeam satellite communication system, onboard resources are limited.Some users in the beam coverage area request HD TV live services, others request voice call services,and still others request video conference services,etc.,and thus the traffic demands among users are different.Since the aforementioned multigroup multicast precoding approaches do not take traffic demands into account, users with higher demand may obtain lower throughput, while users requesting lower traffic may be over-satisfied.It is difficult to flexibly adjust throughput to users’ demands by these precoding methods,which leads to the requested-offered throughput mismatch and thus the waste of resources.Therefore,they are not applicable to the scenarios where there exist differences in users’traffic demands.Ref.17studies the generic optimization framework for multiuser linear precoding design and proposes an iterative algorithm based on alternating optimization to tackle the problem, which considers traffic demands, but only pays attention to the unicast scenario and lacks investigation on the multicast scenario.

In this paper, we investigate the precoding design for multicast multibeam satellite communication systems.Considering the differences in traffic demands among users as well as the importance of fairness, we formulate a multigroup multicast optimization problem to maximize the minimum throughput satisfaction ratio of all users while satisfying per-feed power constraints and traffic demand constraints.Our goal is to provide users with the throughputs that match their demands to achieve proportional fairness.The problem is an NP-hard problem and is non-convex.To deal with the intractable problem, we first reformulate it by introducing an auxiliary variable.Then, semidefinite relaxation is employed to relax the problem.Based on bisection search, we further convert the relaxed problem into a series of convex feasibility problems.Finally,we obtain the optimal precoding vectors by eigenvalue decomposition or Gaussian randomization.Numerical results verify the effectiveness of our proposed algorithm.

The remainder of this paper is organized as follows.In Section 2,we introduce the multibeam satellite multicast transmission system model.Section 3 formulates the multigroup multicast problem and presents the details of the proposed optimization algorithm.Numerical results and performance analysis are discussed in Section 4.Finally, conclusions are given in Section 5.

2.System model

As shown in Fig.1,we consider a multibeam satellite communication system with full frequency reuse, where a single GW cooperates with a multibeam satellite to serve user terminals on the ground.The array fed reflector at the satellite is equipped with Ntantenna feeds and generates G beams to provide services for multiple single-antenna users.In this paper,we assume a single-feed-per-beam architecture13,which is popular in modern satellites such as Eutelsat Ka-Sat.18Thus, the number of beams is set equal to that of antenna feeds, i.e.,Nt=G.First, the GW sends signals to the satellite by the feeder link.Then, the satellite transforms Ntfeed signals into G transmitted signals through an array fed reflector,and radiates them to the ground to form a multibeam coverage area,which are received by user terminals.It is noted that the feeder link is considered ideal, which is a common assumption in related literature.16,17

In this paper, we consider a satellite multicast scenario.By adopting Time Division Multiplexing (TDM), each beam serves a single group of users simultaneously in a given time instant, and thus there are G multicast user groups in total.Suppose each user group contains q users, then, the satellite serves a total of Gq users via multicast communication at the same time.For brevity, let Gkdenote the k - th multicast user group, which is the set of users served by the k - th beam,where k ∊ ｛1 ，2，∙∙∙，G｝ represents the group index.Since each user belongs to only one user group, Gk∩Gl=θ，∀k，l ∊ ｛1 ，2，∙∙∙，G｝，k≠l.The transmit signal intended for all users in group Gkis denoted as skwith unit power, i.e.,， ∀k.Let wk∊CNt×1stand for the precoding vector designed for user group Gk.

Fig.1 A multibeam satellite communication system model.

Then, the received signal at the i - th user in group Gkcan be written as

where hi∊C1×Ntdenotes the channel vector from the satellite to the i - th user in group Gk,and niis the additive white Gaussian noise with zero mean and variance,i.e.,ni～CN 0，,measured at the user’s receiver.The first term of the expression represents the desired signal for this user, the second is the interference from other groups of users, and the third denotes the noise received by this user.

The channel vector between the Nton-board feeds and the i - th user in group Gkcan be modeled as

The scaling parameter ψican be described as19

whereλ isthewavelength,didenotesthedistance betweenthe i -thuserin group Gkandthesatellite,（λ/4πdi）2denotesthe free space loss, Grrepresents the user’s receiving gain, κ is the Boltzmann constant, T is the receiver noise temperature,W represents the user link bandwidth, and κTW denotes the noise power at receiver.Note that the channel is normalized by the noise term κTW, and thus it is assumed that=1.

The multibeam antenna gain can be approximated by the tapered-aperture antenna beam gain model20,21, which is widely used in the research on multibeam satellite systems.14,17The n - th entry of biis given by

where Gmaxis the maximum satellite antenna gain,which indicates the transmit antenna gain observed at the beam center;J1and J3are the first and third order Bessel functions of the first kind, respectively.The parameter ui，nis defined as ui，n=2.07123 sin （αi，n）/sin （α3dB）, where αi，ndenotes the angle between the center of the n - th beam and the location of the i - th user as seen from the satellite; α3dBis the angle corresponding to the half power loss from the beam center, which is a constant.

The phase variation effects between the n - th feed and the i - th user, which comprises different contributions, is defined as

where φi～U（0，2π）denotes the phase offsets due to the radiofrequency signal propagation path.15Due to the fact that the distances between satellite antenna feeds are relatively small compared with the long propagation path from the satellite to one user,13the phases between all the antenna feeds and one user, which refer to φi, are usually considered identical.In other words, φitakes the same value over all the feeds,and is thus only relevant to the user index i.This is a common assumption in multibeam satellite channel models.indicates the phase offsets caused by the payload oscillator, which is independent of the user index i.15

3.Multigroup multicast precoding design

3.1.Problem formulation

With the satellite multicast transmission system model established in the above section, we focus on the fair multigroup multicast precoding based on traffic demands in the following.

According to the signal model in Eq.(1),the received SINR for the i - th user in group Gkcan be expressed as

Then,we denote the data rate for the i - th user in group Gkas Ck，i, which is calculated as

In the multicast scenario, the transmission rate of all users in each group depends on the worst user of the group.We devote attention to the worst user of each multicast group to ensure that satellite services are available to all users instead of only some of them.Hence, the achievable multicast rate,which is the offered throughput,for users in group Gkis given by

Moreover,since the average power of the transmitted signal has been normalized in the above signal model,the transmitted power of the n - th feed is expressed as

In the considered scenario,the system cannot meet the traffic demands of all users.Thus,we take the throughput satisfaction ratio as the design metric, which is defined as the ratio of the offered throughput(achievable multicast rate)to the traffic demand.Taking into account the traffic demands and the fairness among users,we dedicate to the multigroup multicast precoding design with the objective of maximizing the worst throughput satisfaction ratio of all users, and thus all users can achieve the same throughput satisfaction ratio.In this way, all the users can receive fair service, and we can provide users with the throughputs that match their demands.Moreover, the per-feed power constraints and the traffic demand constraints are considered.The optimization problem is formulated as

where Fkindicates the traffic demand for users in user group Gk,which is the requested throughput,and Pnis the maximum available transmitted power of the n - th feed.The optimization objective in Eq.(10a)is to match the achievable transmission rate to the traffic demand to the same extent for all users,which helps to achieve fairness and address the mismatch issue.Eq.(10b) represents traffic demand constraints that limit the achievable transmission rate not to exceed the requested throughput to ensure that the demand is not over satisfied,thereby saving onboard power to avoid resource waste.Considering the difficulties of deploying power sharing mechanisms, we investigate the more realistic power constraints in Eq.(10e), where the power for each feed is restricted by the threshold.The optimization problem (10) is non-convex and NP-hard, making the solution of the problem challenging.

It is difficult to handle the non-convex objective function directly.To simplify the problem, we introduce an auxiliary variable γ as the lower bound of the throughput satisfaction ratio for all the users, such that the optimization problem(10) can be equivalently reformulated as follows:

3.2.Semidefinite relaxation

3.3.Bisection

Rank relaxation makes the optimization problem more tractable;however,problem Prremains nonconvex due to variable γ.Note that when γ is constant,problem Prbecomes a convex optimization problem that can be solved efficiently by using the CVX toolbox.The goal of the relaxed problem Pris to maximize γ, and the optimal value of γ is within an interval.Thus, we can search the interval by solving problem Prwith different γ to find the optimal solution.Hence, by fixing the value of γ,the relaxed problem can be transformed into a series of convex feasibility problems.

For a fixed γ, the feasibility problem is expressed as

To reduce power consumption while checking feasibility,we introduce an auxiliary variable t to transform the feasibility problem as follows:

3.4.Gaussian randomization

Since we relax rank constraints when applying the semidefinite relaxation method, it is necessary to determine whether solution matrices are rank one.The optimal solution usually satisfies the rank-one constraints in the unicast scenario where independent data is transmitted to each user.However, we study the multigroup multicast problem which generally fails to yield unit rank solutions.To this end,the Gaussian randomization method22is adopted to generate an approximate solution to the original problem.

Similarly,problem SPcan be transformed into the feasibility problem SQwith different γ, and then solved by the bisection search method.Problem SQis formulated as follows:

Algorithm 1.Fair multigroup multicast precoding algorithm based on traffic demands.

1.input: hi, σ2i,Fk,Pn,N,ε,i ∊Gk，k ∊ 1，2，∙∙∙，G｛ ｝, n ∊ 1，2，∙∙∙，Nt｛｝2.repeat 3.for γ= γ+γ-/2, solve problem Q if the problem is feasible, then let γ=γ, else let γ-=γ 4.until γ--■ ■G γ<ε;denote the solution to problem Pr as Xopt k k=1 5.if rank Xopt k =1 for all k,compute w*k = ——-λk√ uk by eigenvalue decomposition 6.else: for l=1，2，∙∙∙，N 7.generate the candidates ｛^wk ｝G k=1■ ■G 8.solve problem SQ with different γ to find ——-pk√ ^wk k=1■ ■G k=1 with the optimal objective value 10.output: w*k 9.select w*k■ ■G k=1 = ——-■ ■G√ ^wk pk k=1

3.5.Complexity analysis

Complexity analysis is presented as follows.To obtain an approximate solution to the original problem, it is required to solve the problem Q for N1times and the problem SQfor NN2times, where N1and N2denote the number of bisection search iterations required to solve Prand SP,respectively,with

4.Simulation results and analysis

In this section, we evaluate the performance of the proposed multigroup multicast precoding approach in a multibeam satellite system through numerical simulations.Simulation results are obtained by averaging over multiple channel realizations.In the simulation scenario, we consider a multibeam satellite with G=7 beams and users served by the satellite are distributed uniformly within the coverage area.For each channel realization, we use N=50 Gaussian randomization trials to obtain the approximate solution to the problem, and the accuracy of the search algorithm is set to ε=10-3.Moreover, we set the standard deviation of the payload oscillator phase offsets as χ=10°.Considering the difference in the traffic demands among users,the traffic demands for users in each user group are set to [1.5，1.5，3，3，0.8，0.8，0.8]Gbps.Detailed simulation parameters are shown in Table 1.In the following,we consider the MMSE15algorithm and the SR13algorithm as the benchmark precoding methods for performance comparison.

Table 1 Simulation parameters.

The sum rate of the system is defined as follows:

which represents the sum of the achievable multicast rate for each user group, with the portion that exceeds the traffic demand being excluded.

Fig.2 shows the sum rate achieved by the three algorithms with different per-feed available power.We set the number of users per beam (group) to q=3.It can be seen that the sum rate of all the algorithms increases when the per-feed available transmit power varies from 100 to 250.Numerical results illustrate that the proposed algorithm outperforms the others and shows more significant performance gain with increasing available power.We can observe that at a limited power of 200 W,the proposed algorithm outperforms SR and MMSE by 0.9511 Gbps and 2.3588 Gbps, respectively.It is clear that our proposed algorithm performs better in terms of the ratio of sum rate to total traffic demand.

As shown in Fig.3, we investigate the effect of varying the number of users per beam on sum rate performance.The number of users per beam is varied from 2 to 5, and the per-feed transmit power is limited to 250 W.It can be observed that the sum rate decreases as the number of users per beam increases for all the algorithms.Furthermore, the sum rate achieved by our proposed algorithm is larger than that by the others in the whole region considered.In particular, when q=5, the proposed algorithm achieves around 8% gain over SR, and outperforms MMSE with approximately 30% gain.

Fig.4 demonstrates the minimum throughput satisfaction ratio of all groups of users with different per-feed available power.The number of users per group is fixed to be 3.The throughput satisfaction ratio represents the ratio of the offered throughput to the traffic demand, and here the offered throughput is defined as Rk=min （Ck，Fk）.From the figure,it can be seen that the minimum throughput satisfaction ratio increases with the increase of the available transmit power.It can be also observed that our proposed algorithm outperforms the others.

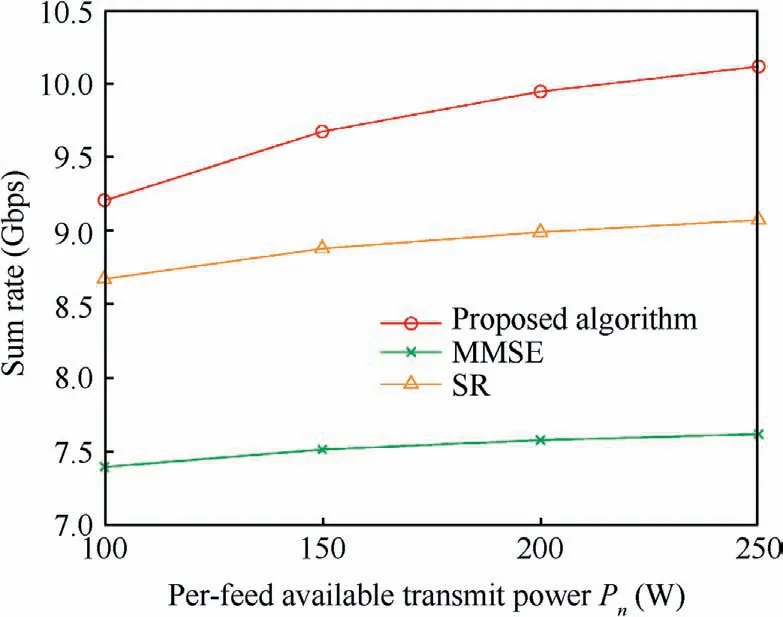
Fig.2 Comparison of sum rate performance of different algorithms with different per-feed available transmit power.

Fig.3 Comparison of sum rate performance of different algorithms with different number of users per beam (group).

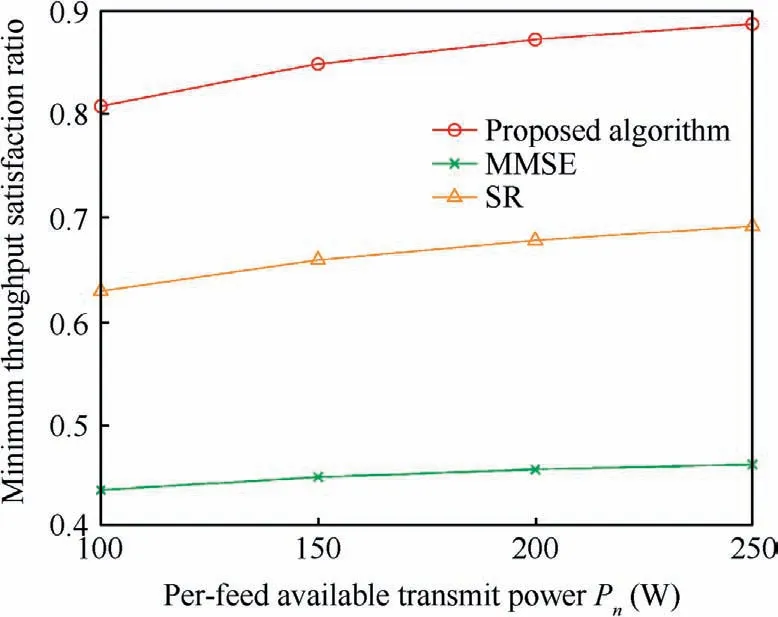
Fig.4 Comparison of the minimum throughput satisfaction ratio of different algorithms with different per-feed available transmit power.

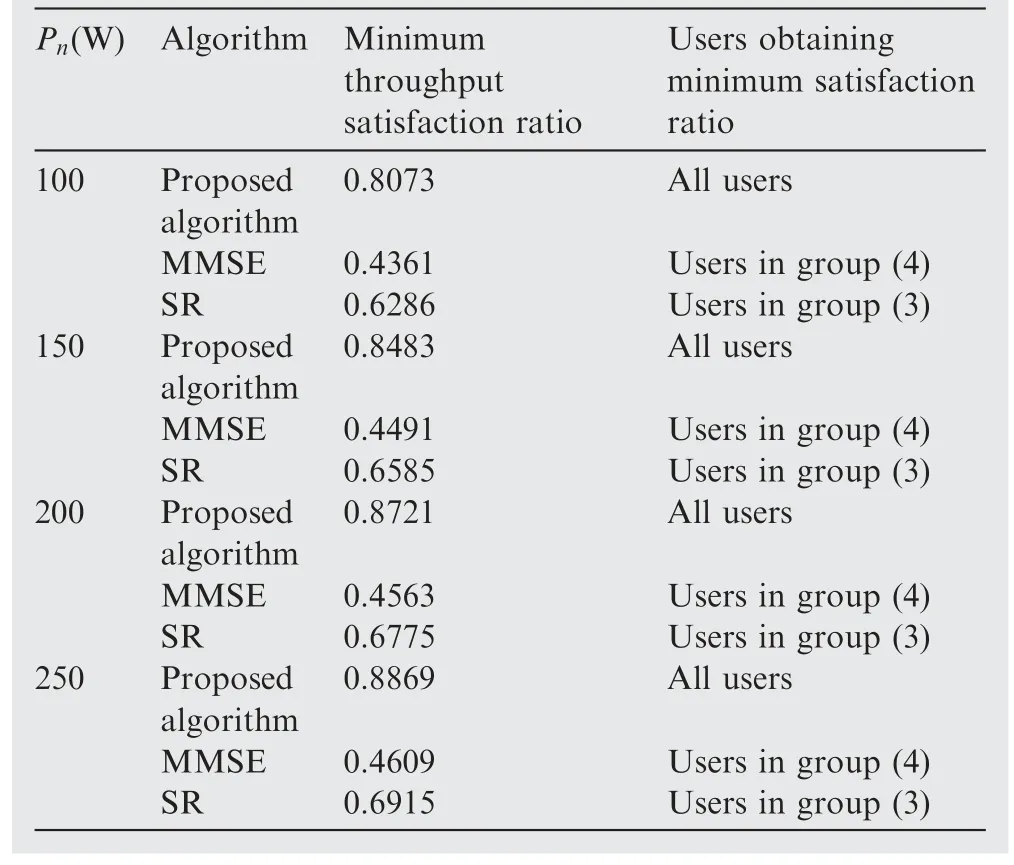
Table 2 Detailed results of the minimum throughput ratio in Fig.4.

Table 2 shows the detailed results of the minimum throughput satisfaction ratio in Fig.4.It can be seen that the proposed algorithm achieves equal throughput satisfaction ratio for each group of users, while the users with the traffic demand of 3 Gbps obtain the minimum satisfaction ratio when we apply SR or MMSE.This indicates that the proposed algorithm can guarantee fairness among users,and can provide better service for the users with higher traffic demand compared with the other two algorithms.

Fig.5 shows the minimum throughput satisfaction ratio of the three algorithms when the number of users per beam varies from 2 to 5.Here, the per-feed available transmit power is set to Pn=250 W.As can be seen from the figure, increasing the number of users per beam leads to the decrease in the minimum throughput satisfaction ratio.The reason is that all the considered algorithms experience the achievable rate loss as the user number per beam increases.Considering fairness among users, the proposed algorithm improves the performance of the worst user.Therefore, the proposed algorithm obtains performance gain over the other two algorithms in terms of the minimum throughput satisfaction ratio.

The mismatch of the system is calculated as

which describes how well the achievable multicast rate matches the traffic demand.

In Fig.6, we compare the mismatch performance of the three algorithms with different per-feed available transmit power.We assume three users per beam.It can be seen from the figure that when the available transmit power changes from 100 W to 250 W, the mismatch of the proposed algorithm decreases, which implies that the matching degree with the traffic demand increases.In addition, we can observe that for MMSE and SR, the mismatch tends to increase with the increasing available power, and is always higher than that of the proposed algorithm.This indicates that the proposed algorithm is more advantageous in matching the traffic demand.

Moreover, Fig.7 depicts the impact of different number of users on the mismatch performance.We set the per-feed available transmit power to be 250 W.With the increase of the number of users per beam, the achievable rate of users decreases, and thus the mismatch of the proposed algorithm shows an increasing trend; while for SR and MMSE, despite the decrease in the achievable rate, the portion that originally over-satisfies the traffic demand decreases, resulting in the decrease of the mismatch.However, we can observe that the proposed algorithm matches the traffic demand better in the whole considered region.With the number of users per beam set to 5, the proposed algorithm still outperforms MMSE and SR by 0.2180 and 0.5051,respectively,in terms of the mismatch performance.

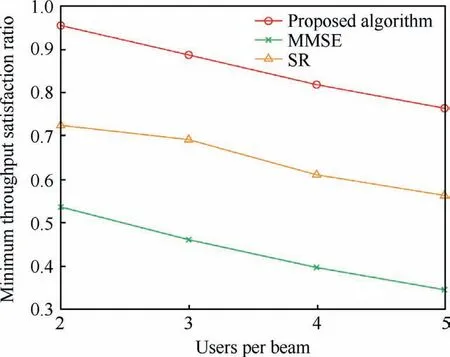
Fig.5 Comparison of the minimum throughput satisfaction ratio of different algorithms with different number of users per beam (group).

Fig.6 Comparison of the mismatch performance of different algorithms with different per-feed available transmit power.

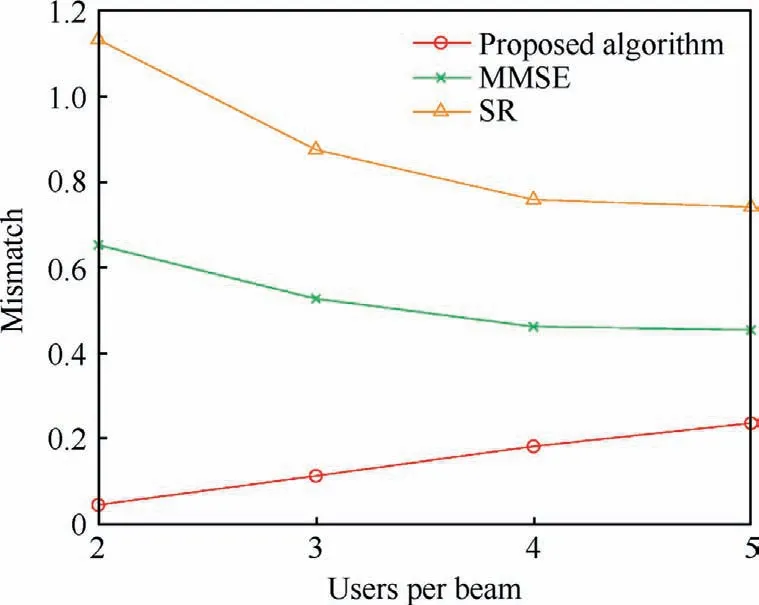
Fig.7 Comparison of the mismatch performance of different algorithms with different number of users per beam (group).

5.Conclusions

In this paper, we investigate the multigroup multicast precoding design in multibeam satellite systems.Taking into account the difference in traffic demands and fairness among users,we aim to maximize the minimum throughput satisfaction ratio under per-feed power constraints and traffic demand constraints.First, we introduce an auxiliary variable to simplify the proposed optimization problem.Then, we adopt the semidefinite relaxation method combined with the bisection search strategy to transform the intractable problem into a series of convex feasibility problems.Finally, Gaussian randomization is employed to deal with rank-one constraints.Numerical results demonstrate the effectiveness of the proposed algorithm in improving the flexibility and fairness of the system.It is shown that our precoding algorithm is more suitable for the scenarios with different traffic demands.

Declaration of Competing Interest

The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.

Acknowledgement

This study was supported by the National Key R&D Program of China (No.2020YFB1806800).