Flamelet-like models applied in scramjet combustors: A state of art and prospect
To TANG, Zhenguo WANG, Yuhui HUANG, Mingo SUN,*,Hongo WANG, Guoyn ZHAO, Jingfei YU
a College of Aerospace Science and Engineering, National University of Defense Technology, Changsha 410073, China
b Equipment Project Management Center, Equipment Development Department, Beijing 100089, China
KEYWORDS
Abstract Developing supersonic combustion models with efficiency, accuracy and practicality is important foundation to deeply understand the complex combustion processes in scramjet engines.Characterized by efficiency and intuition, the flamelet-like models are widely used models in computational combustion methods.However, the supersonic combustion flow field has the nature of strong compressibility, multiple modality, and multiple scales,which poses a great challenge to the traditional flamelet-like models with fixed boundary conditions, and then the complex chemical reaction mechanisms that may face will impose additional computational burden.In this context,this paper reviews the flamelet-like models used in scramjet engines, and summarizes prominent issues in the application practice, including modeling partially premixed combustion, defining progress variable, solving temperature efficiently, evaluating assumed Probability Density Function(PDF) models, and treating mixture fraction variance.Furthermore, possible prospects and directions of improvements are proposed and highlighted for the flamelet-like models.To fully describe the physicochemical scenario and address the raised challenges, these improvements are dedicated to dealing with the compressibility,temperature rise,time-scales,species of interest,multi-inlet combustion, the progress variable definition, and the higher Mach number flight condition.
1.Introduction

Nomenclature C Progress variable~C′′2 Progress variable variance Da Damko¨hler number E Total specific energy e Internal energy FI Flame Index Ka Karlovitz number Ma Mach number p Pressure Rg Gas constant t Time Tu Unburned gas temperature Y Species mass fraction YC Unnormalized progress variable Z Mixture fraction~Z′′2 Mixture fraction variance δf Flamelet thickness ρ Density φ Laminar flamelet database~φ Turbulent flamelet database χ Scalar dissipation rate χst Stochiometric scalar dissipation rate γ Specific heat ratio ˉ˙ωC Source term of progress variable Superscripts- Reynolds average~ Density-weighted Favre average Subscript tab Tabulated value in flamelet database
In recent years, hypersonic flight has become a hotspot technology in the aerospace field, and the scramjet engine is the power core of its air-breathing propulsion system.A typical scramjet is generally composed of an inlet, an isolator, a combustor,and a nozzle.As the source of oxidizer,the supersonic inflow is still entering the combustion chamber at a supersonic speed through the pre-compression of the inlet and isolator,and the fuel is gathered for combustion in such a circumstance.Obviously, the fuel injection, mixing, ignition, flame stabilization and propagation within a very short residence time is quite challenging.Moreover,the turbulent combustion process in a supersonic combustion chamber is inherently complex,which involves complex interactions between turbulence and chemical reactions.Turbulent pulsation can significantly enhance fuel–air mixing and subsequent flame stabilization,but it can also lead to flame outs if turbulent dissipation is excessive.At the same time,combustion can increase the intensity of turbulent pulsations through flow expansion and even trigger combustion oscillations.The increase in temperature in turn raises the molecular viscosity of the reaction stream,and then may bring a certain inhibiting effect on turbulence.Highly nonlinear chemical reactions can significantly increase the component gradients and thus change the micro-mixing process.Conversely,the fuel–air mixing state can greatly affect the chemical reactions.Therefore, an in-depth understanding of the supersonic turbulent flow, mixing and combustion processes is essential for the design and performance optimization of scramjet engines.
However,due to the limitations of experimental conditions,it is difficult to obtain enough research data and some largescale experiments are difficult to undertake.In this context,numerical calculations are an effective means to study the internal flow and combustion characteristics of scramjet engines.This method can obtain rich details of the flow field to reveal the mechanism and have the advantage of being efficient and flexible to optimize the design.In recent years, with the rapid development of computer technology and Computation Fluid Dynamics/Computation Combustion Dynamics(CFD/CCD), the numerical methods have gradually become as important as ground experiments and flight tests for developing hypersonic flight technology.
With respect to combustion phenomena, the occurrence of chemical reactions requires full mixing of fuel and oxidant on the molecular diffusion characteristic scale, but the computational grids of both RANS (Reynolds Averaged Navier-Stokes simulations)and LES(Large Eddy Simulations)cannot fully resolve this part of information.Therefore, how to accurately model the interactions between turbulent mixing,molecular diffusion and chemical reactions on the unresolved scale becomes the key to the numerical simulation of turbulent combustion.In addition,the turbulent flow in scramjet combustor has comparable timescale range to that of the chemical reactions.The shock waves and expansion fans can also result in strong coupling of speed, pressure, and temperature, thus influencing the flame stability and combustion heat release.In this context, the multiple scales, many species, strong compressibility and complex combustion regimes,bring great challenges to supersonic turbulent combustion modelling.
Considering combustion models, the flamelet-like models and the PDF-like models are two most widely researched and applied categories.1For different combustion regimes and different application purposes, these two types of models have their own advantages and limitations.The main advantage of PDF-like models is its good theoretical basis and wide applicability, while its drawback is the intensive calculation quantity.As the flamelet-like models can provide relatively low computational burden with accurate results, thus can be widely used in engineering practice.
From the perspective of chemical reaction, combustion involves many components and reactions, forming a highdimensional thermodynamic state space.It is unwise to solve it directly; therefore, the general approaches are to reduce its dimension or the stiffness of equations.The two types of approaches can be summarized as chemistry reduction and dimension reduction, as shown in Fig.1, corresponding to two types of combustion models,namely the PDF-like models and the flamelet-like models.1Representatives of the PDF-like models include the T-PDF1model, LEM2,3model, ODT4,5model, and MMC6,7model.These models usually rely on the chemical mechanisms reduced by DRG8or CSP9method,which can lessen the transported species and decrease the stiffness.The flamelet-like models restrict the species into a lowdimensional manifold and can avoid dealing with complex rigid chemical reactions in CFD calculations by tabulating a chemical database in advance.Representatives of this type are the FPV model, FGM model, SF model, and UFPV model.Generally,for different combustion regimes and different application purposes,these two types of models have their own advantages and limitations.The main advantage of the PDF-like models is its good theoretical basis and readily applicability, but its drawback is the intensive calculation quantity against complex chemical mechanisms.While the flamelet-like models can deal with complex chemical reactions with relatively low computational burden, thus can be widely used in engineering practice.Note that not all combustion models are listed and discussed.And for simplicity, the detailed comparison between these models can be referred to in many previous review articles.1,10–14

Fig.1 Hierarchy of combustion models used in RANS or LES alculation (DRG—Directed Relation Graphs; CSP—Computational Singular Perturbation; T-PDF—Transported PDF; LEM—Linear-Eddy Model; ODT—One-Dimensional Turbulence; MMC—Multiple Mapping Conditioning;FPV—Flamelet/Progress Variable;FGM—Flamelet Generated Manifold;SF—Steady Flamelet model;UFPV—Unsteady Flamelet/Progress Variable; pre-PDF— presumed PDF method).
From the computational point of view, the flamelet approach is very attractive, for the chemistry complexity can be handled through a very simple configuration ahead of the CFD calculations.By this way, the species of the entire combustion system are expressed in a low-dimensional manifold,where the mixing and reaction states can be simply parametrized.However, its main limitations also stem from these strong assumptions.In addition, the flamelet model was originally proposed in laminar diffusion combustion.Although it was gradually extended to supersonic turbulent combustion with compressibility corrections,there are still some issues that need to be solved for its application in supersonic turbulent combustion.The first issue is whether the flamelet model is applicable in the supersonic combustion flow field, and how to handle the regimes that the flamelet concept is not valid.The second one is to deal with the complex physicochemical process in the scramjet combustor involving shocks, local extinctions/re-ignitions, etc.Thus, how to modify the model according to the insight of physicochemical scenario becomes critical in accuracy improvement.Besides, there are also some practical issues of concern in the application of the flameletlike models.
The scope of the paper is to summarize the practical issues of concern by analyzing the state of the art in the simulations of scramjet combustion using flamelet-like models,and then to draw out possible prospects for model improvement.The outline of the paper is:the basic theoretical introductions are presented in Section 2.Then the practical issues critical to the application in scramjet using flamelet-like models are summarized and discussed in Section 3.Finally, the improvement directions for the flamelet-like models applicable to the scramjet are drawn out in Section 4.
2.Concepts of flamelet-like models
The flamelet-like models, or the flamelet models, generally include the Steady Flamelet(SF)model,the Flamelet/Progress Variable (FPV) model, the Flamelet Generated Manifolds(FGM),unsteady flamelet model,Unsteady Flamelet/Progress Variable (UFPV) model, and Representative Interactive Flamelet (RIF) model.Their theoretical bases are mostly identical, and for simplicity, the SF model and the FPV model are selected here for illustration.
2.1.SF model and FPV model
The steady flamelet model was originally proposed by Peters15on the basis of laminar diffusion combustion.While for the phenomena of turbulent diffusion combustion, under the assumption that the flame thickness is much smaller than the Kolmogorov scale of turbulence,the reactive layer of the flame front is considered to be much thinner than the smallest vortex,thus maintaining a local laminar flame structure.The intuitive illustration has been depicted in the review of Urzay,16as shown in Fig.2.In the scale approaching the flamelet thickness δf, the local structure of the flame can be simplified as a onedimensional counterflow diffusion flame, and the maximum temperature distribution in the manifold is shown in the right part of the figure,which is vividly called the s-curve.This manifold can be obtained by solving the flamelet equations under specific boundary conditions in the mixture fraction space.Tabulated as laminar flamelet database, the species mass fraction and the temperature can be directly accessed through mixture fraction Z and stochiometric scalar dispassion rate χst,namely Yi(Z ,χst)and Tmax(Z ,χst).Here,the stochiometric scalar dispassion rate χstplays a role in distinguishing different chemical reaction states.In this way, the high-dimensional thermochemical information can be expressed through reduced dimensions in the manifold, which shows the essence of the high efficiency of the flamelet model.
However, in practical CFD calculations, the quantities stored in the laminar flamelet database need to be processed in advance by the assumed PDF functions for obtaining their filtered values, that isdZdχst, where P(Z ,χst) is the assumed PDF function.Thus,for turbulent flamelet models, in addition to the scalar dispassion rate, another two quantities that must be solved are the mixture fraction Z and its variance ~Z′′2.The former is solved as a conservation scalar using the transport equation, which essentially represents the local equivalence ratio, while the latter can be solved by an alternative algebraic model, and they have been clearly defined by Pitsch and Peters.17Since the scalar dissipation rate in this model can only map the upper half branch of the s-curve, it is therefore called the steady flamelet model.
Consequently, in order to completely distinguish all the states in the solution of flamelet equations, Pierce and Moin18proposed the FPV model which introduce a parameter called reaction progress variable to remapping the s-curve.Specifically, the reaction process from pure mixing state to the fully burned state (near the infinitely fast chemistry) along the scurve can be mapped through the progress variable from value 0 to 1 uniquely, thus the filtered database can be expressed asTypically, the definition of the reaction progress variable is obtained through a linear weighted combination of the end products or reactants.For example,as given by Ihme and Pitsch19in their simulation of Sandia flames D and E, the progress variable is expressed as YC=YCO2+YCO+YH2O+YH2.In FPV model,the progress variable C can be solved by a transport equation,and its source term can be obtained by querying the flamelet database.
2.2.Examination of flamelet assumptions in supersonic combustion
The flamelet concept and associated approaches are originally established under low Mach number diffusion combustion conditions.However, in a typical scramjet combustor, the kinetic energy is comparable to the heat released by reactions,and significant coupling of physical quantities such as pressure and temperature can be observed due to the interactions between shock waves, turbulence, and flames.In this context,the conventional flamelet models may require further detailed corrections to better match the actual physicochemical scenario.But before that, the flamelet model hypothesis, or rather, the applicability of the flamelet model in the scramjet combustor must be examined.For non-premixed flames,depending on the magnitude of the Karlovitz number (Ka)and the Damko¨hler number (Da), three combustion regimes can be categorized: the first one is in the flamelet regime of Ka < 1 and Da > 10, the second is in the thin reaction zone regime of 1
As shown in Fig.3(a),20the joint PDF distribution of Da number and Takeno Flame Index (FI) in HIFiRE 2 model scramjet are depicted and colored with heat release rate.It can be observed that the main heat release zone is located in the upper left region (Da > 10 and FI <0), thus the flamelet assumption is generally valid and the diffusion combustion is dominant.Shin and Sung21simulated the hydrogen fueled and the kerosene fueled strut-based model scramjets and plotted the combustion regime as shown in Fig.3(b).As can be seen,most of the reaction zones are consistent with the flamelet assumption.However,as reported by Yao et al.22in Fig.3(c),the flamelet regime and the thin reaction zones occupied about 2/3 of the whole combustion system in a model scramjet operating at a total temperature of about 1500 K.These are largely consistent with the physicochemical scenario of the flamelet concept, whereas the other 1/3 is classified as the slow chemistry regime, which may require a more appropriate model to describe.As pointed out by Mura et al.23in a study of a JISCF(Jet In Supersonic Crossflow)combustion chamber with a Mach 2 inlet and a total temperature of about 1700 K, the combustion in the near-wall region is mostly subject to the slow chemistry regime, as shown in Fig.3(d), while the combustion away from the near-wall region is mostly in a broken flamelet regime (or thickened-wrinkled flame regime).
Certainly, the definition and calculation of the characteristic parameters for combustion mode classification may differ in different studies.For example, the chemical reaction timescale in Da number could be calculated by the chemical reaction source term or ignition delay time, etc.However, it is easily concluded from the above studies that,most of the combustion systems within the actual scramjet combustors cannot be simply classified into a single combustion regime, but the flamelet regime is undoubtedly the most representative one among these regimes.And this is in accordance with the conclusions of Ingenito and Bruno.24By analyzing the effects of Mach number and compressibility on turbulent combustion,Ingenito and Bruno24pointed out that in most cases the smallest scale vortices in supersonic combustion are still larger than the thickness of the flame front reaction zone.Therefore, the supersonic combustion can be approximately described by the flamelet regime.However, for those combustion regions that fall outside the description of the flamelet assumption,the combustion model may need to be specially modified or coupled with other models to improve the computational accuracy.
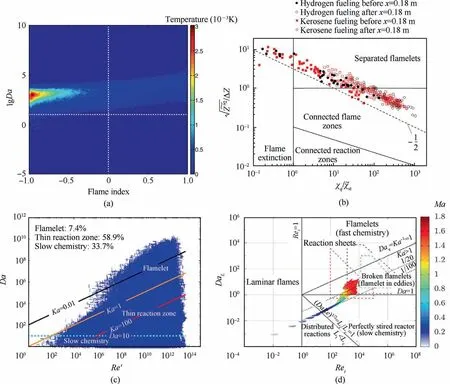
Fig.3 Combustion regimes in different scramjet combustors given by(a)Saghafian et al.20,(b)Shin and Sung 21,(c)Yao et al.22,and(d) Mura et al.23.
In addition, due to the close coupling of many physical quantities in the combustion flow field,the complex supersonic combustion phenomena in scramjets brings high demands on the applications and improvements of the flamelet-like models.For example, in the supersonic combustion flow field, the kinetic energy is on a comparable order of magnitude to the heat released by the chemical reactions, so a direct extension of the low Mach number flamelet model to supersonic combustion would cause significant errors.In this regard, Oevermann25proposed a method that the temperature is solved implicitly from the internal energy, which is one of the most important improvements of the flamelet model for considering compressibility.Due to its simplicity and accuracy, this method has been widely adopted in supersonic flamelet models.However, considering the complexity of supersonic combustion in scramjets, the application details and the tailored improvements of the supersonic combustion flamelet models shall be far from limited to this.
3.Key issues in applications
For simplicity, Table 120,21,25–67summarizes the current reported applications of flamelet-like models in scramjet engines, including the simulated configurations (scramjet engines),fuels, computational methods, and the specific combustion models.Note that, not all typical supersonic combustors are numerically studied using flamelet-like models.A prominent example is the NASA SCHOLAR combustor24,68–70, which is not included in Table 1 as a result.And more comments on recent advances in scramjet engines can be found in Refs.71–76.
As can be seen from the table,in recent years,there are several features in the applications of flamelet-like models in scramjets: firstly, there are more studies on hydrogen-fueled scramjet engines, among which the DLR strut combustor is the most representative one.For example, Fig.4 shows the numerical results of DLR struct combustor calculated by Fureby,26which is in good agreement with the experiment.The reasons for choosing this configuration include two main aspects.On the one hand, the experiment records abundant data including temperature, velocity, and velocity pulsationsat different locations.Thus,it has become the preferred experiment for many scholars to validate and develop supersonic combustion models, such as Oevermann25and Shan et al.27.On the other hand, the hydrocarbon fuel usually has a more complex chemistry, which may require reconsideration of the flamelet tabulation, temperature calculation, and model accuracy.
Secondly,the Flamelet/Progress Variable (FPV) model has been applied more often than the Steady Flamelet(SF)model.The main reason is that the FPV model employs a complete flamelet solution within a similar model framework.The FPV model adopts the unsteady branch in the s-curve, thus,its theoretically higher computational accuracy makes it more beneficial to calculate an extra transport equation for the progress variable.
Last but not least,there are almost no reports of blind tests,that is, predicting the combustion flow field under the given boundary conditions while without the experiment data.This is the best fit for the practical application demands.If the blind test of scramjet engines can be realized, the importance of supersonic combustion calculation dynamics will be significantly enhanced in the field of hypersonic propulsion technology, and the design cycle of scramjets will be significantly shortened.

Fig.4 Numerical results of DLR struct combustor using steady flamelet model.26
To sum up,during the development of the last two decades,the flamelet-like models have seen a number of successful practices in scramjet engines, which include both some small-scale model engines and some real scramjets.And with the improvement of the models and the advancement of the computational power, the computational accuracy has been gradually improved.However, to our knowledge, when using the flamelet-like models in supersonic combustion, there are at least five practical issues that need to be further discussed.
3.1.Partially premixed combustion
As for a typical scramjet combustor,the supersonic inflow and the fuel stream enter the combustor through separate channels,thus this non-premixed fuel and air configuration seems to make diffusion combustion the dominant mode undoubtedly.And in the studies of Zhang,77Drozda,67Tang,35Wu78et al.and many others, diffusion combustion is indeed dominant in the combustion flow field of scramjets.To distinguish the diffusion combustion and the premixed combustion, the most intuitive parameter is the Takeno Flame Index,79which is determined by the direction of the oxidant gradient and the fuel gradient, that is,For example,in Fig.5(a) and (b), Wu78and Liu80et al.depicted the flame index in the scramjet combustors of Micka and Driscoll81as well as Gamba and Mungal,82respectively, indicating the dominance of diffusion combustion.Similarly, in Fig.5(c)and (d), the distributions of flame index in DLR struct combustor and the HIFiRE 2 combustor given by Shin and Sung21and Saghafian et al.,20respectively, also show that the diffusion combustion is dominant.It can be seen that, in these cases, the premixed flame mainly exists in the undermixed but ignited core fuel flow,while the shear layer or mixing layer outside are mainly non-premixed.
However,in the scramjet combustor,the premixed combustion is present together with diffusion combustion in the reaction flow field.And in some cases,the proportion of premixed combustion may increase, such as the predominance of nearwall combustion or the evident self-ignition effects.As shown in Fig.6, in the two combustors studied by Potturi and Edwards83and Mura et al.23, the near-wall combustion accounts for a high proportion, which is mostly dominated by premixed combustion, and the high enthalpy inflow also contributes to the self-ignition effects.It can be seen that,the premixed combustion mainly exists in the boundary layer,separation regions and recirculation zones,84and as the flight Mach number increases, the premixed flame becomes more important in combustion stabilization.In this context, a more physically realistic description of such a combustion flow field is a flamelet model considering partially premixed regime.
To discriminate the combustion modes,the prevailing practice is to introduce a mode differentiation factor and use it as a weight for diffusion and premixed combustion, such as the studies of Knudsen and Pitsch85–87, See and Ihme88, and Hou et al.30.The frameworks of these studies all add a transport equation of the progress variable variance to the FPV model in order to further consider the turbulent chemistry interactions in premixed combustion.And this partially premixed method requires solving the 1D non-premixed and pure premixed flamelet equations in advance for tabulating the corresponding database.In the latest study, Shan et al.52established a transport equation for the mode differentiation factor (called premixed weighting coefficient in the paper),which can replace the previous algebraic model used by Knudsen and Pitsch85–87and others and retain the historical effects.As shown in Fig.7,52the temporally averaged distributions of the premixed weighting coefficient in a cavity model combustor are exhibited and compared.It can be seen that the proposed transported multi-regime flamelet model shows a smoother result and does not miscalculate in areas without fuel.However,the direct use of the mode differentiation factor to weight premixed and non-premixed database in these studies still lacks a physicochemical basis and needs further investigation.
Certainly, the subfilter variance of progress variable can also be considered in diffusion combustion.For example, as shown in Fig.8, Cao et al.32used the presumed δ-PDF and β-PDF for the progress variable C,respectively,and compared their effects in the studies of DLR strut combustor.Using δ-PDF for the progress variable C means ignoring the effects of the progress variable variance ~C′′2, which implies that the flame state in a single computational cell is resolved.However,in the regions where strong turbulent and chemistry interaction exists, the reactions might not be resolved in LES grids, thus,the progress variable variance should still be properly modeled.It can be seen from Fig.8 that the second central moment information of the progress variable is beneficial to improve the accuracy of the flamelet model.But it should be noted that,this requires additional calculation of the progress variable variance both in the CFD solver and in the pre-tabulation stage.
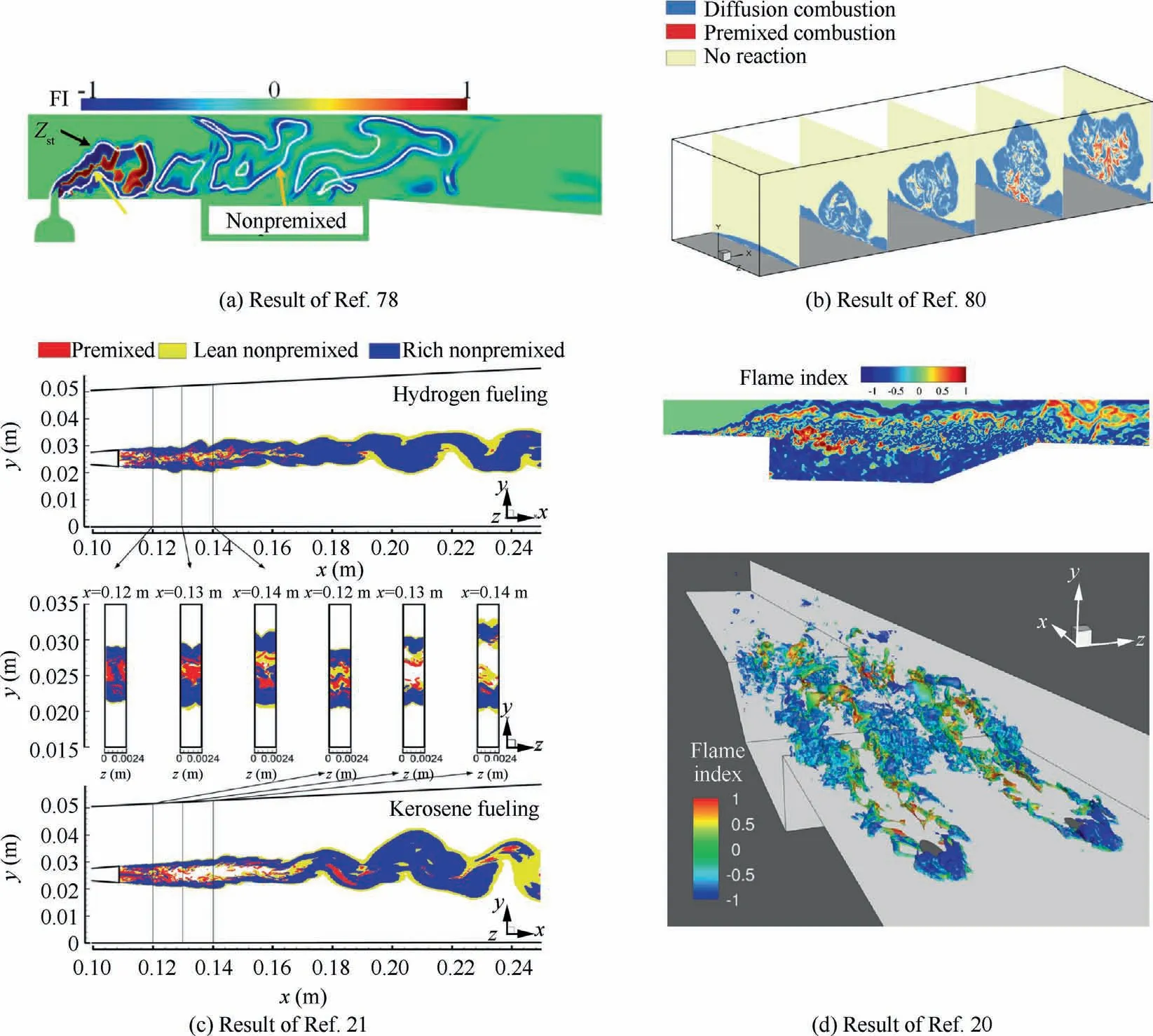
Fig.5 Flame index distribution in different scramjet combustors.

Fig.6 Combustion mode in supersonic combustors given by (a) Potturi and Edwards83 and (b) Mura et al.23
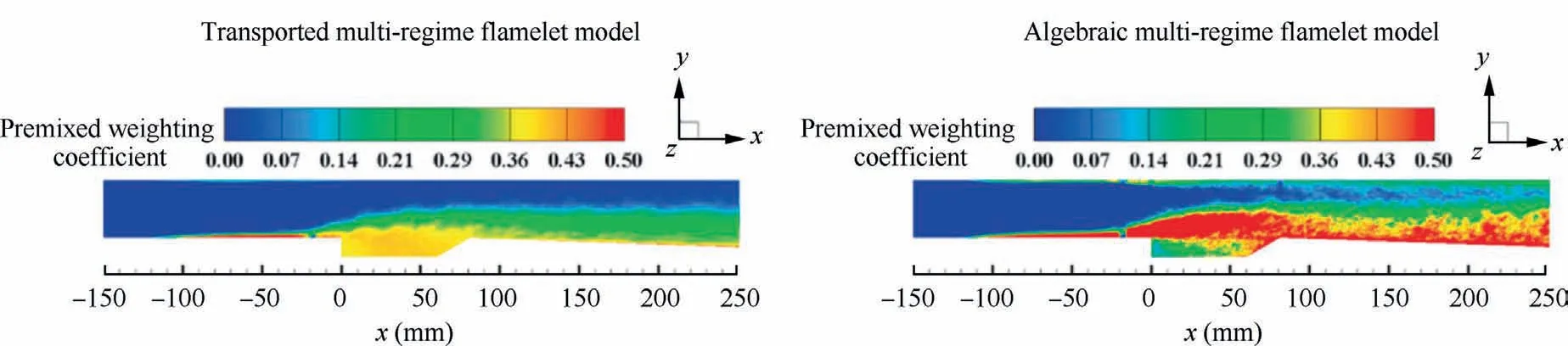
Fig.7 Comparison between mode differentiation factor calculated by transport equation and algebraic model.52
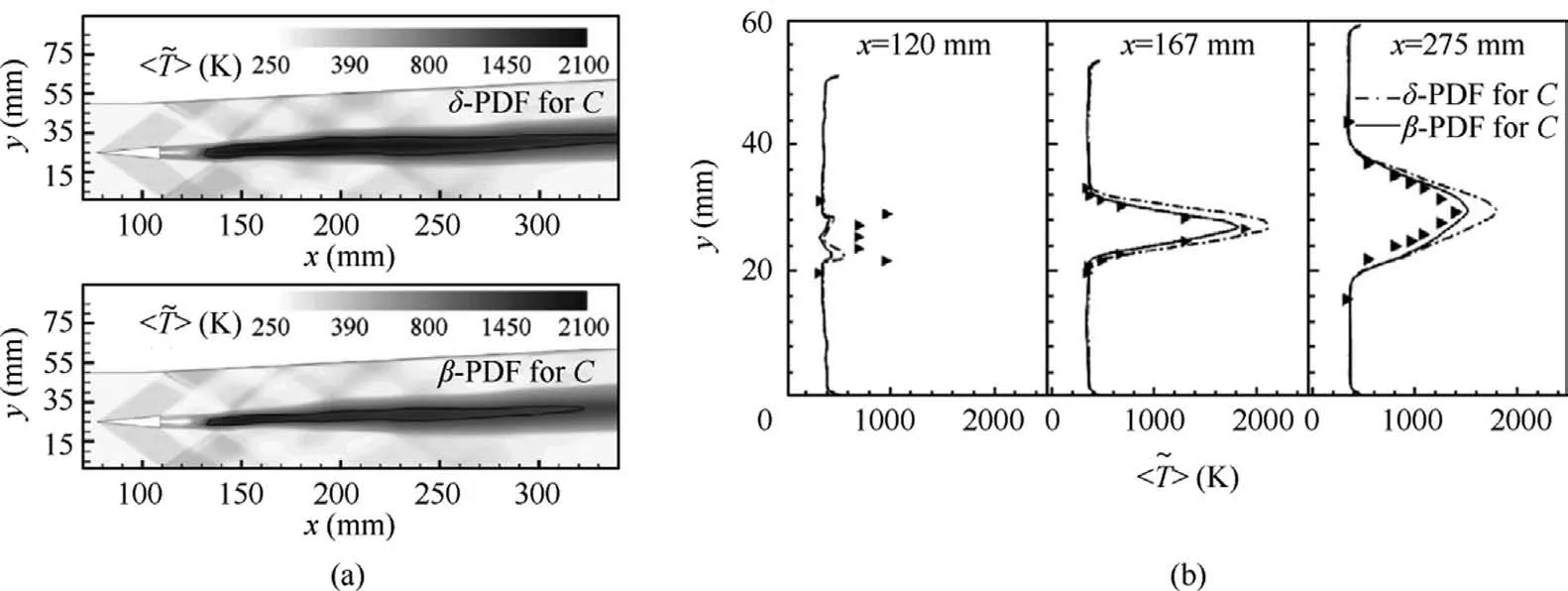
Fig.8 Comparison of presumed δ-PDF and β-PDF for progress variable C in simulation of DLR strut combustor32: (a) Contours of time-averaged temperature; (b) Temperature profiles.
3.2.Reaction progress variable
As an important concept in FPV or FGM model,the progress variable is not only a dimension of the flamelet database, but also reflects the extent of the combustion process: the value 0 indicating no reaction and 1 indicating a fully burned state.It is usually defined by a linear weighted combination of major products or reactants.But since this definition has a weak mathematical foundation, in many studies, it is often directly given according to users’expertise.In a physicochemical sense,the progress variable, as a reaction tracker and an indexdimension for the flamelet database as well, has an important impact on the accurate description of chemical reaction processes.For instance, the importance of progress variable was emphasized by Quinlan et al.66in the study of HDCR dualmode scramjet combustor.However,this study only compared the computational results of several commonly used expressions of progress variables.Certainly,the‘‘best”progress variable varies depending on the specific purpose.The definition of progress variable is indeed an open question, but it still has some prevalent criteria that need to be met, and on this basis,some extra optimization targets can be added.According to Ihme et al.89and many other studies,monotonicity,continuity and completeness are the currently accepted basic requirements for progress variables,which make the mapping of progress variables to the thermal-chemical state space injective and surjective mathematically.
As for treating the choosing of progress variable as an optimization problem, Ihme et al.89were the first to propose the basic criteria for selecting of progress variables, and to establish a framework for optimizing progress variables.Najafi-Yazdi et al.90used the Principal Component Analysis (PCA)method to downscale the high-dimensional thermochemical space and obtained the weights of the species in progress variable.Niu et al.91proposed an optimization objective of minimizing the variation of the components over the progress variable, but this method was tested only in one-dimensional premixed flames.Besides, its high computational time cost is believed to be a drawback.Pru¨fert et al.92applied the optimization method to laminar methane and oxygen fuel flames following Niu’s idea.They proposed using genetic algorithm to minimize the gradient of species, which can make the changes of species smoother in the progress variable space.But Vasavan et al.93believed that this species gradientbased objective cannot capture transient phenomena, such as the ignition process in diffusion flames.Therefore, their optimization objective was to minimize the interpolation error of the progress variable source term in the ignition induction phase, and the results reproduce the ignition delay with high accuracy.They also pointed out that, the progress variable source term, the scalar dissipation rate, or the Damko¨hler number were the appropriate parameters worth considering.And following this idea, Chitgarha et al.94added an additional constraint of minimum Damko¨hler number based on the consideration of the mixing and reaction time scale,which may be beneficial to improve the prediction accuracy of the rich or lean combustion reactants at high strain rates.Tang et al.60adopted a heat-release-based objective for optimizing the progress variable and demonstrated its effects in a RP-3 fueled scramjet combustor.Duboc et al.95,96optimized the progress variable to ensure the self-similarity properties of minor species, but the transport equation of progress variable in the study is similar to the species equations.Besides,Zadsirjan et al.97proposed a method to define the progress variable by the absolute cumulative quantity of species,which is a new definition that can satisfy the monotonicity.But the drawback is the additional solutions forwhich may require modifications to the solver of the flamelet equations.
To sum up, the above-mentioned optimization methods with various objectives, however, are mainly applied in low Mach number combustion.While for supersonic combustion,the effects brought by different progress variable definitions may be more significant,60,66and it is then necessary to optimize the progress variable for better accuracy.
3.3.Solving temperature under a complex chemistry
As a common fuel for actual scramjet combustors, kerosene,or its substitute, has a complex chemistry, which is often described by chemical mechanisms containing hundreds or thousands of species.As a result, the process of solving temperature would be computational costly.This is because,unlike the flamelet models in low Mach number that directly look up the temperature from the tabulation, most of the supersonic flamelet models are based on the temperature solving method proposed by Oevermann,25which requires calculating the enthalpy of all species and solving the temperature implicitly.Obviously, too many species in a complex chemical mechanism may lead to unaffordable computational overhead.An excessive database volume will also take up too much memory.With this regard, there are generally five approaches to choose from.
The first one is to use the reduced chemical mechanisms directly.This approach is undoubtedly simple and easy-toaccomplish.One can directly use the simplified mechanisms that can be publicly consulted, such as semi-global mechanisms.However, Yao et al.61–64pointed out that this may affect the calculation results.For example, as shown in Fig.9, Fureby98compared the calculated results using different H2mechanisms and concluded that that the simplified mechanism may not accurately predict ignition delay times.One can also use the method of virtual chemistry as demonstrated by Cailler99and Maio100et al.
The second approach is to store only representative species with large mass fractions in the flamelet database,and directly ignore the other minor species, as in the studies of Wehrfritz,101Kahila,102and Sula103et al.Although somewhat arbitrary, this would be a very simple and efficient method if one could accept the inevitably errors caused by the method.
The third approach is to create virtual species as substitutions, referring to the studies of D’Errico,104Lucchini,105,106and Maghbouli107et al.They solved the mass fractions of virtual species based on constraints such as elemental conservation and energy conservation, thus equating a large number of real species to several virtual species.This approach is applicable to any complex mechanism, but the drawbacks are that the pre-processing is a bit complicated and the information on the spatial distribution of the real species will be completely missing.
The fourth approach is using the Compressible FPV(CFPV) model proposed by Pecˇnik49and Saghafian44et al.The ingenuity of this approach is that it uses the following Eq.(1) to solve the temperature, where the subscript ‘‘tab”means the quantity needs to be pre-tabulated, and the coefficient a~γ,tab= d~γ/d~T.
The advantage of this method is that the temperature solution does not depend on species information,so the number of species stored in the flamelet database can be determined exactly according to the needs of the users.The CFPV method has been successfully applied in some cases66,108, such as the HIFiRE 2 model combustor simulated by Saghafian et al.20(shown in Fig.10).However,a salient issue is that the numerical treatment of the coefficient a~γ,tab must be handled with great care, otherwise significant numerical instability may be introduced.
The last approach is to calculate temperature explicitly using the heat release rate ~Q as a source term of the energy equation (see Eq.(2)), as practiced by Ladeinde,109Tekgu¨l,110Sula,103and Wu78et al.
This approach can also allow the temperature calculation to be independent of the species information, which relies on the pre-tabulated heat release rate.However,Li et al.111noted that this direct addition of the heat release rate to the equation may be not applicable to high-speed reaction flows,which may overpredict the heat release due to neglecting transient effects.
3.4.Assumed PDF models

Fig.9 Numerical results of DLR strut combustor using different H2 mechanisms.98
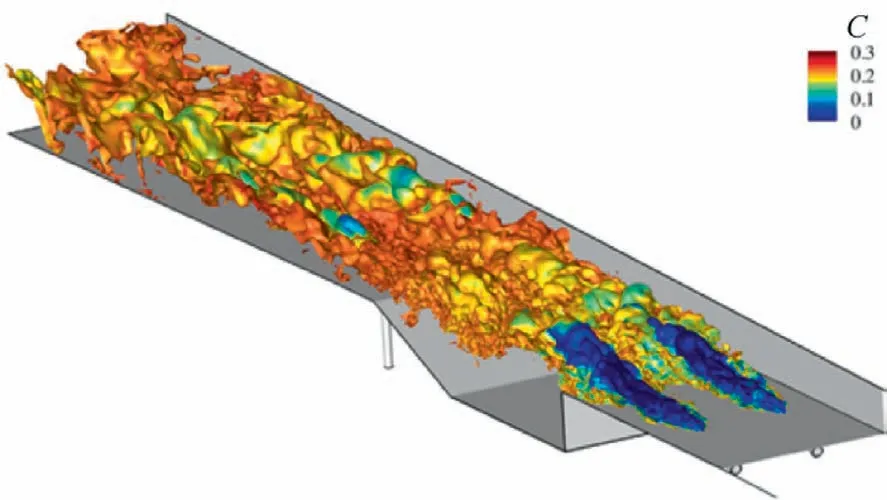
Fig.10 Stochiometric iso-surface colored by progress variable in HIFiRE 2 model combustor.20
Considering the combustion phenomena, the chemical reactions occur at the molecular level smaller than Kolmogorov scale, so additional subfilter models are required for reactions occurring at the sub-grid level.In FPV model,since the flamelet database is tabulated before CFD calculations,the assumed PDF method is adopted to consider the turbulent/chemistry interactions in advance.Pierce and Moin18proposed to use the assumed β-PDF for the mixture fraction Z and the δ-PDF for the progress variable C mathematically.As Girimaji112pointed out, the beta function is well suited for use as a model for mixture fraction, because it captures both the bimodal distribution at the fuel and oxidant ends before molecular diffusion and the single-peak distribution after molecular diffusion.Therefore, in the flamelet-like models applied to turbulent combustion, almost all studies chose this model as the presumed distribution function for the mixture fraction Z, such as Donini113and Han114et al.And even for multi-stream combustion chambers, the beta distribution has general applicability.However, Popov115also pointed out the prediction failure of the β-PDF around Z = 0 and Z = 1, thus proposing a substitute function named the Probability Space Diffusion (PSD) distributions.This alternative distribution predicted more accurately in turbulent/chemistry interaction phenomena such as partial extinction and reignition.Definitely, the Statistically Most Likely Distribution(SMLD)of Ihme19and Coclite38–40et al.,among others,is also an optional approach,although the implementation is complex and has fewer applications.
For simulations of partially premixed combustion,the subfilter variances of both the mixture fraction and the progress variable require additional modeling.And the most straightforward approach in this case is to choose beta distribution for both Z and C independently, as practiced by Hou,30Shan,52Cao32et al.However,some studies116,117indicate that the use of β-PDF for progress variable seems to over-predict the averaged reaction rate.Alternative presumed PDF functions include Gaussian function,118copula function,119,120and the joint PDF function.121But in general, β-PDF is still a model with a high degree of generality and accuracy.
3.5.Mixture fraction variance
To obtain the filtered values of all tabulated parameters in advance, a presumed β-PDF is commonly used as illustrated above.Thus, the mixture fraction variance is generated as a new dimension of the flamelet database and as a must-solved quantity in CFD solver.There are generally three methods to solve the mixture fraction variance as follows: the first is to solve it directly using its transport equation; the second is to solve it by an algebraic model, such as quadratic filtering of the mixture fraction based on the scale similarity hypothesis;the third is to solve the squared mixture fractionby the transport equation, and then calculate the mixture fraction variance by.Among these, the first two methods are more commonly found in the reported literature.For example, Ladeinde122and Gao123et al.calculated the mixture fraction variance directly by its transport equation, while Shin29and Thakur124et al.used an algebraic model alternatively.But obviously,as pointed out in the comparative studies of Kemenov,125Ventosa-Molina,126and Techer127et al., the computational accuracy of the first method is generally higher.But as an alternative,the second method offers a lower computational cost but introduces a certain amount of errors.As for flamelet-like models, this subfilter variance becomes even vital for its direct influence on the database indexing, and in turn,the intensity of local chemical reaction will affect the subgrid variance,which may further magnify the error.An example given by Tang et al.35is shown in Fig.11.Therefore, if there is a need for computational accuracy,the transport equation method for solving the mixture fraction variance is more recommended,as is the case for the progress variable variance.
4.Prospects for improvements
4.1.Compressibility corrections
In the flamelet-like models, the flamelet database is usually tabulated at a fixed pressure according to the configuration to be simulated, such as the averaged pressure of the combustor estimated from experiments.Obviously,it is an approximation, whereas in a supersonic flow field with large pressure fluctuations,this approach would be far from the actual physical scenario and may introduce some errors.To address this issue, the state-of-the-art of the studies mainly focus on two major corrections of the flamelet-like models: the first aspect is the pressure-related scaling of the progress variable source term,which is mainly from the perspective that pressure significantly affects the chemical reaction rate.For diatomic molecular fuels,the chemical reaction rate is approximately squared with respect to the pressure.Thus,the modification of the progress variable source term is reasonable.As shown in Table 2,20,27,32,44,45,48,122,123,128–131the reported pressure scaling formulas for the progress variable source term ˉ˙ωCare listed, where the subscript ‘‘tab” indicates that this variable is pre-tabulated under a fixed pressure and stored in the database.For instance,the correction proposed by Saghafian et al.20shows significant improvements as depicted in Fig.12(a),where the original flamelet model cannot capture the upstream flames induced by local pressure raise.In Fig.12(b) and (c),Shan27and Gao123et al.demonstrated the effects of their pressure correction methods, respectively, but due to the small pressure fluctuations in DLR strut combustor itself,the effects of the corrections are not well reflected.
The second types of pressure corrections are to expand the pressure as an extra dimension of the flamelet database.For example, one can take a cue from internal combustion engines,108,132,133and directly use the pressure as a dimension of the database.In addition, due to the similarity of the spatial distributions of species or progress variable source term under different pressures, an associative formula can be established.For example, Mittal and Pitsch134adopted the following Eq.(3) to scale the species based on local pressure, where the coefficients aY,1and aY,2are pre-calculated using the database built under different pressure.
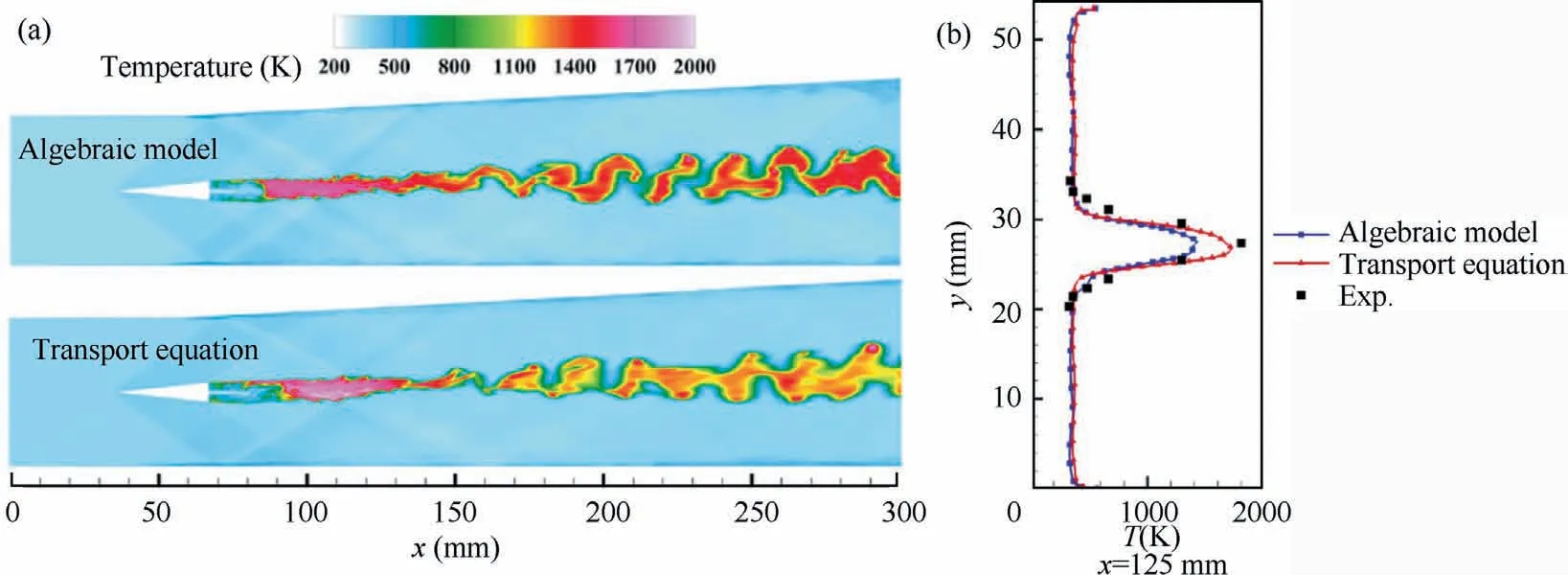
Fig.11 Calculated results of FPV model using a transport equation and an algebraic model for the mixture fraction variance35: (a)Temperature contours in center plane; (b) Temperature profiles.

Table 2 Formula summary on pressure scaling corrections for progress variable source term.
Similarly, Zhao et al.50,51adopted the following Eq.(4) to build the correlations between the database built under different pressure.And its improvements were demonstrated51as shown in Fig.12(d).
In general, the pressure-related corrections are quite necessary and effective, especially for the combustion in scramjet engines.In the future, more pressure corrections are expected to be proposed and applied to further address the problem of chemical reaction rate change under strong compressibility.
4.2.Temperature corrections
When solving the flamelet equations, the temperature boundary conditions of oxidizer and fuel are usually specified based on the actual inlet conditions.However,for a complete scramjet engine containing a long isolator, this practice would deviate from physical reality.As Matsuo et al.135pointed out(Fig.13), the supersonic inflow gradually decelerated and heated up through the action of the pre-combustion shock train in the isolator,where the kinetic energy is partially transformed to thermal energy.Thus, by the time the mainstream reaches the main combustion zone, the temperature of the mainstream will be already far from the inlet temperature, as is the case for the pressure.In addition, the inherent compression and expansion of the flow field would also cause the temperature fluctuations.Considering these effects, the temperature correction is also very important for the flamelet-like models.
Some of the corrections for the progress variable source term are also considered to have taken into account the temperature impacts, as shown in Table 2.In addition, the CFPV method is also believed to have considered this issue, since its key coefficient a~γ,tab =d~γ/d~T requires at least two flamelet database built under different temperature boundaries.And its temperature calculation Eq.(1) uses the local energy which can take into account the internal energy change of the mainstream through the pre-combustion shock train.However, so far, in the field of supersonic combustion, there has not been a correction dedicated to this problem, but some studies related to internal combustion engines provide a good idea.That is, the unburned gas temperature Tu, is solved additionally using a transport equation.And this approach can be found in the studies of Galpin,136Lucchini,105,106,133Maghbouli,137Zhou138et al.This practice can provide a reasonable restoration of the temperature at different locations before the reaction starting, thus it might be a baseline for the temperature corrections in scramjet engines.
4.3.Time-related models
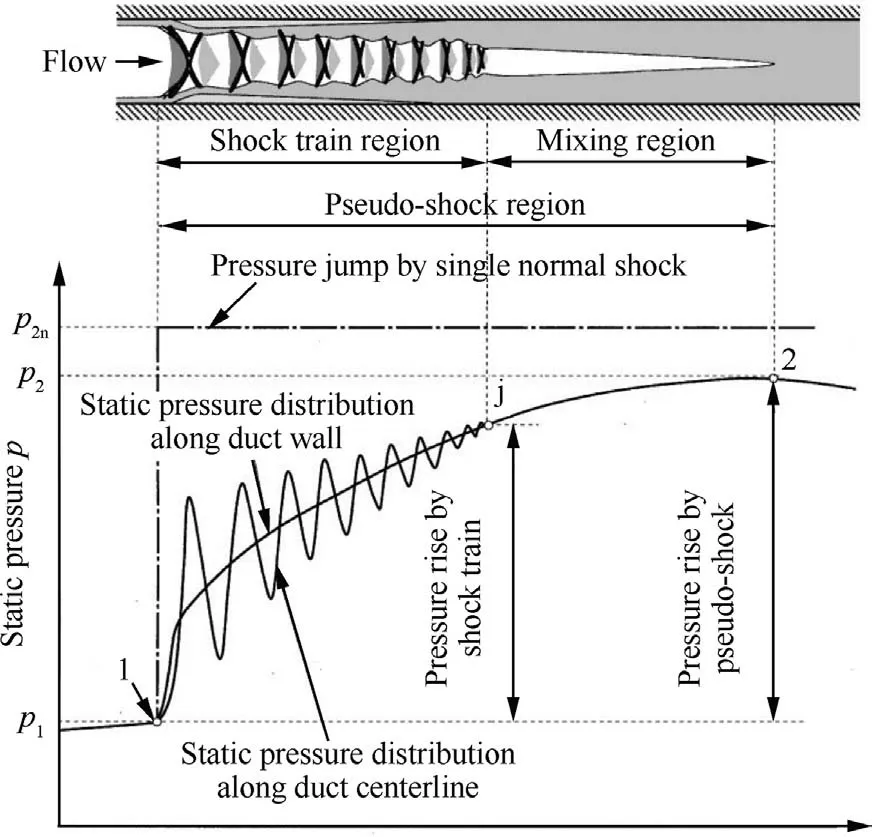
Fig.13 Schematic static pressure distribution in a constant-area duct.135
The ignition and flame stabilization in scramjet engines have long been a concern.Induced by high enthalpy inflow with high Mach number, the auto-ignition phenomena become significant, and the timescales of the chemical reactions are worthy of attention.The early reaction process from ignition is mainly the decomposition of the fuel with little heat release,so there is a time delay before significant heat release starts.139In some scramjet combustors where the auto-ignition effect is obvious, the auto-ignition phenomena coexist with the flame propagation, and even the auto-ignition plays a major role in flame stabilization.And then the combustion model should consider the time-related information.At present, there are mainly two types of methods: the first one is the Unsteady FPV (UFPV) model proposed by Pitsch and Ihme,140which tactfully introduced an extra dimension of scalar dissipation rate.Successful practice has been reported by Ihme and See141in an auto-ignition prediction of methane/air jet diffusion flame,as shown in Fig.14.Similar successful studies have been done by Luo142and Bajaj et al.143
Another approach is to couple the Tabulated Kinetic of Ignition (TKI) model, which stores the ignition delay time in a separate database and describes the auto-ignition using an independent progress variable in CFD calculation.Domingo et al.144successfully realized this method and applied it in a lifted methane jet flame.Knop et al.145also proposed a new formulation of the TKI model with an independent progress variable for the auto-ignition process.However, both of these methods have rarely been applied in supersonic combustion.
In addition, Go¨ktolga et al.146,147proposed an intriguing approach named Multi-Stage FGM (MuSt-FGM), which adopted one progress variable (adding species like HO2and CH2O) in preignition stage and another progress variable (using end products or reactants) in the main combustion stage,as illustrated in Fig.15.146This method improved the prediction of species through creating a database and defining a progress variable in each of the two phases; therefore, it is promising to be extended to supersonic combustion.
4.4.Other prospects
Firstly, in a combustion system, different sub-reactions have different life cycles and time scales, for example, NOx, a kind of pollutant of concern in internal combustion engines, has a relatively long timescale.148For these special species or other species of interest, additional coupling of the corresponding species transport equations in the flamelet models may be able to further improve the prediction accuracy.Ihme and Pitsch149first coupled the NO transport equation in the FPV model and gave the expression of its source term with respect to the production and consumption rates of NO.Similarly, Efimov150and Honzawa151et al.coupled an extra CO transport equation in the flamelet model.Although it is rare to see this method applied to supersonic combustion, it is equally worthwhile to extend this method to the supersonic combustion in scramjet engines if there are species of interest, such as CH4and OH.In addition, the Hybrid Transported-Tabulated Chemistry(HTTC) proposed by Duboc et al.95,96is also a noteworthy approach, especially for the application of chemical mechanism including hundreds of species.This approach constrains the gradient of species on the progress variable and tabulates the minor species with self-similar properties,while the important species of interest are transported for the solution.It cleverly exploits the self-similarity of minor species, but at present it has only been tested in zero-dimensional premixed flames,and its extension to diffusion flames requires further study.Recently, Bo¨ttler et al.152also affirmed that this concept is promising to improve the flamelet model accuracy by transporting major species additionally.
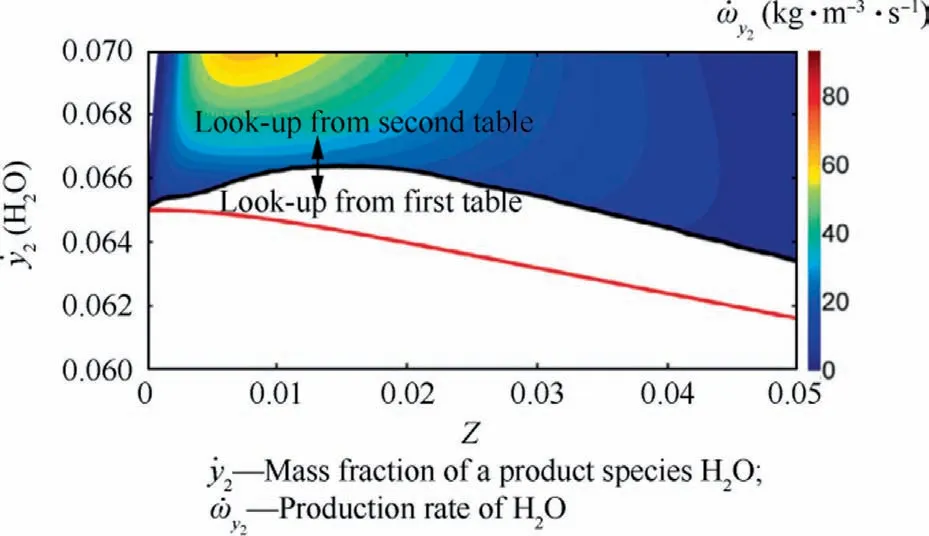
Fig.15 Tabulation details of MuSt-FGM method.146
Secondly, technologies such as multi-stage combustion,supplemental combustion and multi-fuel combustion may become the key combustion technologies for future scramjet engines flying in a wide range of Mach numbers,which usually involves multiple-inlet combustion.For example, the simplest configuration is one inlet for air and two inlets for fuel in the combustor, like the HIFiRE 2 scramjet shown in Fig.16.16If the secondary stage uses a different fuel from the primary one,this reactive flow field itself and its numerical simulations become much complex.To address this issue,Hasse and Peters153first develop a two mixture fraction flamelet model based on a three-scale asymptotic analysis, and successfully carry out simulations of turbulent diffusive combustion in a diesel engine.Following this framework,Doran,154Gomet,155Yu156et al.and others have also successfully simulated low-speed multi-inlet combustion.And additionally, Ihme and See157also combined the two-mixture fraction system with the FPV model and tested it in LES simulations with a MILD combustor.Although rarely applied in supersonic combustion, such methods have a great practical engineering interest.And the key issues include the solution of subfilter variances and the choice of suitable progress variables for different fuels.
Thirdly, the definition of progress variable may need further investigation.In the FPV model,the most mathematically well-defined is the mixture fraction, by contrast, the progress variable is a more idealized indicator of the reactions.And perhaps the most significant limitation of the progress variable is precisely the weakening of its reaction indicator role in complex supersonic combustion fields.Choosing a simple question as an example, are the expressions of the progress variables at different pressures in the combustion flow field the same? Or can the extent of chemical reactions at different pressures be expressed in terms of the productions of several selected species?Whether the same progress variable is consistently representative at different stages of a chemical reaction? Similar questions remain and need to be answered based on in-depth understanding of the physicochemical properties of the supersonic combustion flow field.In a word,for a complex combustion system containing different chemical reaction stages,different combustion modes, and different temperature/pressure states, using only one scalar to distinguish is bound to be a struggle, thus, increasing the dimensions of the flamelet models or coupling other combustion models may be an inevitable choice to improve the model accuracy.
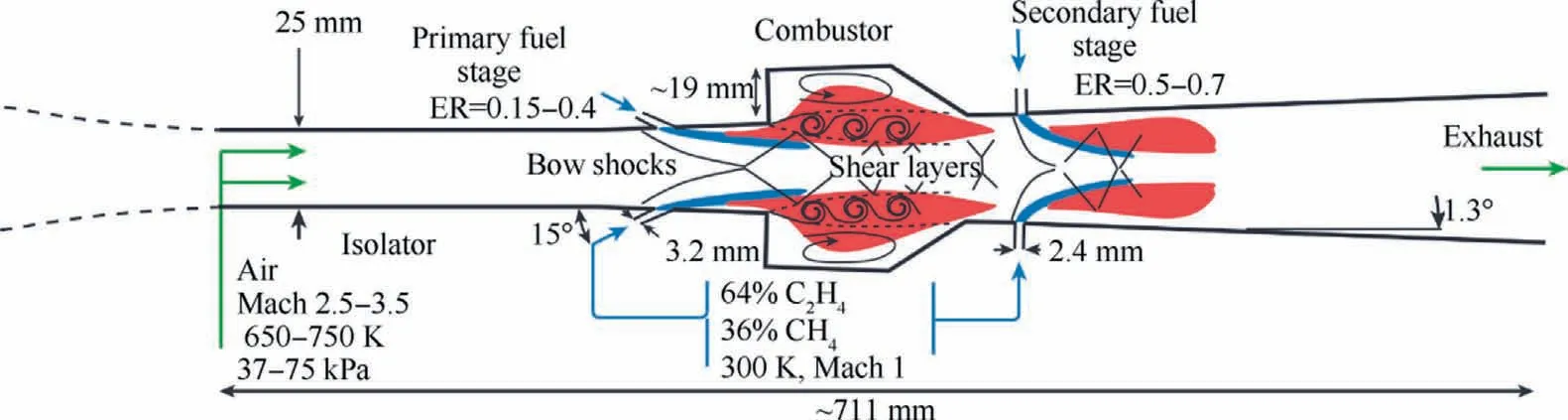
Fig.16 Scramjet configuration of HIFiRE 2.16
Furthermore,when it comes to hypersonic flights,i.e.,flight Mach number more than 8, the challenges hidden behind are multiple.First of all, the prominent one is the obvious compressible effects, as illustrated in Section 4.1.In this regard,the possible model improvements are building-up a relationship between the tabulation and the pressure or enthalpy or temperature.Secondly, another prominent phenomenon is the auto-ignition effects,which may even account for the flame stabilization.In these regions where auto-ignition occurs, the assumption of flamelet model is on longer valid.This restriction makes it necessary to couple additional models or make special targeted corrections.A possible example is coupling the auto-ignition tabulations or time-related models.In addition,the choice of chemical mechanisms may also require special consideration.On the one hand, natural addition of atomic oxygen and nitric oxides into high-enthalpy flows will significantly cut down the ignition delay time.Therefore, the chemical reactions on species like atomic oxygen (O) and nitrous oxide(NO)should be taken into account in both chemical mechanisms and simulations,as emphasized by the studies of Hash et al.158and Fontan Moura.159On the other hand,some minor species (such as HO2and CH2O) are of great importance for the description of auto-ignition phenomena.The distribution of these species may require close attention when capturing the positions where auto-ignition occurs.In this context, Boivin et al.160modified the chemical reaction rate of the three-step reaction mechanism with the autoignition effect targeted, and they successfully simulated an autoignition-stabilized jet flame using this modified mechanism.Wu161,Yao,62Fureby,162and Nilsson163et al.also investigated the influence of chemical mechanisms on supersonic combustion.However, for the flamelet-like models, the adopted chemical mechanisms can be quite detailed, but the O and NO in oxidizer should not be neglected in chemical tabulation.Note that,the required consideration for thermal nonequilibrium phenomena in hypersonic flow goes far beyond these.As the flight Mach number increases, the energy relaxation process will become significant, and thus coupling additional models for describing the vibrational temperature may be of necessity.164,165
Without doubt, some improvements in coordinate with the combustion models are also noteworthy, such as the wall heat transfer modeling, which is however beyond the scope of this study.
5.Summary and conclusions
In this survey, an attempt is made to review the flamelet-like models used in scramjet engines and summarize the prominent issues in applications.The last two decades has seen its growing use in scramjet simulations, and its development in supersonic combustion is still emerging.Due to its efficient and intuitive nature, this type of models is bound to become one of the most important means in supersonic combustion simulations, even in the era of a burgeoning computational power.Successful model improvements and remarkable application practices are summarized and analyzed, including the efforts in modeling partially premixed combustion, defining progress variable, solving temperature efficiently, evaluating assumed PDF models, and treating mixture fraction variance.
However, the flamelet-like model still needs more tailored improvements to describe the corresponding physicochemical scenario properly and completely,which also precisely requires a deep understanding of the complex combustion flow field in the scramjet combustor.In the future work, according to the characteristics of the specific combustor or the insight of the combustion mode,the flamelet-like model applicable to scramjet can be reasonably modified in many aspects, including velocity, pressure, and temperature.These modifications may also draw on relevant experimental studies and low-Machnumber flamelet models.
By summarizing the literature, the following conclusions can be drawn:
(1) The flamelet-like model allows high-dimensional and strongly stiff chemical reactions to converse into lowdimensional manifolds prior to CFD calculations, thus greatly facilitating the simulation practice.However,there are still some reaction zones in supersonic combustion that do not satisfy the flamelet assumption, such as the slow chemistry zone.And in the future,hybrid combustion models or other appropriate modifications may address this deficiency.
(2) In the past two decades,the flamelet-like model has been widely used in scramjet engines, but its efficiency still requires further improvements.For example, the temperature solving process can be further simplified when using complex chemical reaction mechanisms, meanwhile,the database structure and its queries may be also worth optimizing.
(3) Although the flamelet-like model has a nature of physical intuition, it has not yet maximized its physical consistency in supersonic combustion.The paradox is the incomplete match of a fixed-database model to the complex physicochemical problem in the scramjets, which leads to a discrepancy between the simulations and the real combustion process.For example,as for a combustor with a high proportion of premixed flames, a partially premixed flamelet model should be considered.In the future work,to improve the accuracy and applicability in supersonic combustion, the flamelet model should be tailored to the actual physicochemical scenario with further modifications.
(4) The application context of scramjet engines further endows the practical demand for model improvements.In the future, attention should also be paid to the phenomena and characteristics of experiments on scramjet engines in order to make appropriate corrections to the combustion model.For example, the precombustion shock train in the isolator can be considered as a part of the temperature corrections.Similarly,when auto-ignition effects or pressure fluctuations are evident,corresponding corrections for the flamelet model are also expected.
(5) One of the biggest limitations of the flamelet-like model is its low dimensionality, that is, using only 2–3 dimensional features to represent the complex supersonic combustion flow field.Its difficulties and limitations are obvious.For instance, the progress variable C is quite an idealistic parameter to indicate the extent to which the reaction proceeds at different temperatures and pressures.In the next phase,extending the dimensions of the flamelet model or hybridizing other combustion models may become important directions for improvement.
(6) For applying to hypersonic flight with higher flight Mach number, the flamelet-like models require multiple corrections.These additional corrections should be accounted for the compressible effects, the autoignition phenomena, the chemical mechanisms in high enthalpy flows,and the thermal non-equilibrium effects.
(7) Most combustion models,including flamelet models,are currently at the stage of relying on experimental results to set simulation parameters in advance or perform prior calibration.In the future, it is expected that efficient, accurate and adaptive combustion models will be developed and applied to the computational combustion of scramjet engines to achieve blind tests.
Declaration of Competing Interest
The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.
Acknowledgments
This work was supported by the National Natural Science Foundation of China (Nos.12002381 and 11925207), the Science and Technology Foundation of State Key Laboratory,China (No.6142703200311), the Scientific Research Plan of National University of Defense Technology in 2019, China(No.ZK19-02).
 CHINESE JOURNAL OF AERONAUTICS2023年10期
CHINESE JOURNAL OF AERONAUTICS2023年10期
- CHINESE JOURNAL OF AERONAUTICS的其它文章
- Experimental investigation of typical surface treatment effect on velocity fluctuations in turbulent flow around an airfoil
- Oscillation quenching and physical explanation on freeplay-based aeroelastic airfoil in transonic viscous flow
- Difference analysis in terahertz wave propagation in thermochemical nonequilibrium plasma sheath under different hypersonic vehicle shapes
- Flight control of a flying wing aircraft based on circulation control using synthetic jet actuators
- A parametric design method of nanosatellite close-range formation for on-orbit target inspection
- Bandgap formation and low-frequency structural vibration suppression for stiffened plate-type metastructure with general boundary conditions
