顺应理解 整体架构
张万洁


初中课堂教学模式大多是以教材内容分课时讲授为主。以课时为单位进行教学设计容易让教学内容碎片化,在解决问题过程中学生容易产生思维断裂,不利于对知识形成整体认知。而单元教学设计尝试将本质相同或有内在关联的内容安排在一个课时进行整体设计,突出知识体系的逻辑性和整体性,保证了教学的连续性,有利于学生数学能力和数学核心素养的培养。本文以苏科版数学八年级上册“一次函数”为例,与大家一起探讨单元教学的设计。
一、教学目标
1.探索实际问题中的数量关系和变化规律,了解常量、变量和函数的概念,体会“变化和对应”的思想;了解函数的三种表示法(表达式法、列表法、图像法);能结合图像分析简单的函数对应关系。
2.理解一次函数的概念,能够画出一次函数的图像,根据一次函数的图像和表达式理解函数的性质(数形结合的思想)。
3.经历“把实际问题抽象为函数”的过程,应用函数的概念和性质解决具体问题,感受函数模型思想,学会运用函数思想,站在新的高度和角度审视和反思问题;利用函数思想认识和刻画客观世界中的运动变化特征,提升数学建模等核心素养。
二、教学过程
1.揭示本質,单值对应
情境1:播放奥运会男子百米飞人决赛的视频。
师:在百米测试中,当时间t确定时,速度V是否确定?唯一确定吗?
生1:可以唯一确定。比如,当t=14s时,V≈7.1m/s。
情境2:给出百米测试的得分表。
师:当时间t确定时,得分d是否确定?唯一确定吗?
生2:可以唯一确定。比如小明,男,当用时14.0s时,得8分。
情境3:图1是百米测试那天的气温变化图。
师:在这个变化过程中,当时间t确定时,温度T是否确定?唯一确定吗?
生3:也可以唯一确定。比如,在上午11点时,温度为12℃。
师(追问):以上三种情境刚好对应函数的三种表示形式,它们有什么共同点?
生4:当时间t确定时,无论是速度、得分,还是温度,都唯一确定。
【设计意图】笔者通过创设情境,让学生了解函数的三种表示形式,并通过设置问题引导学生思考变量和因变量的唯一对应关系,揭示函数概念的本质。笔者认为,函数概念及思想应该渗透在函数学习的每一个过程中,让学生在潜移默化中构建函数思想。
2.画图探究,细化过程
师:以一次函数y=2x为例,怎样画出它的图像?你是怎么想的?说说你的想法。
教师对学生进行分组,小组经讨论,共同得出所经历的步骤:列表、描点、连线。
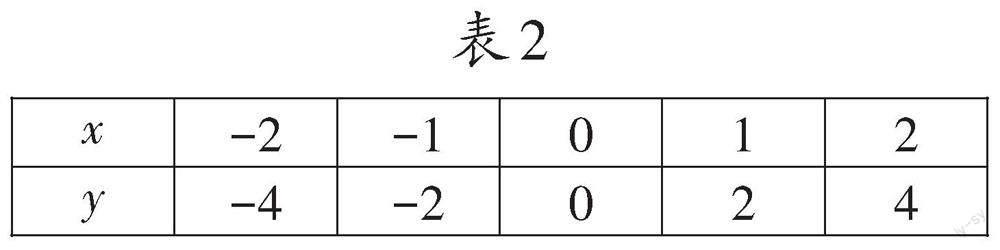
生5:我们小组首先进行取点,在取点过程中发现取的点是杂乱无章的,所以我们通过列表的方法(如表2),按照从小到大的顺序取了5个点。然后建立直角坐标系,在坐标系中描出这5点,最后顺次连接。
【设计意图】笔者以一次函数为例,让学生体验函数图像的绘制过程。在探索一次函数图像的过程中,让学生感受函数同时兼有的三种表示形式。列表、描点、连线是研究函数图像的一般方法。学生通过小组合作的形式,在绘制函数图像的过程中,发现问题,解决问题,加深了对函数图像的理解,进一步揭示了函数概念的本质。
3.数形结合,变换图像
师:再次尝试画出一次函数y=2x+4的图像,你有什么新发现?
生7:图像画出后,我发现,y=2x+4的图像也是一条直线,并且与y=2x的图像平行。
师:我们如何验证呢?
学生通过思考、合作探究,对特殊的一次函数进行证明,证明如下:
如图3所示,已知在y=2x+4上有两个特殊点A(0,4)、B(-2,0),在y=2x取点C(2,4), 过点C作垂直于x轴的直线,交x轴于点D(2,0),易证△AOB≌△CDO,从而得到AB∥CO,则直线y=2x+4与y=2x平行。
师:那么,对于任意的两条直线y=kx与y=kx+b,当b≠0时,两直线是否平行呢?请同学们给出证明。
生8:同理,在y=kx+b取两个特殊点A(0,b)、B[-bk,0],在y=kx取纵坐标为b的点C[bk,b],过点C作垂直于x轴的直线,交x轴于点D,易证△AOB≌△CDO,从而得到AB∥CO。
【设计意图】笔者让学生先从易于证明平行的两条直线出发,再到k值相同的任意两条直线,让学生理解k值相同的两条直线平行的具体原因,体会由特殊到一般的证明过程,有利于学生数学逻辑思维能力的培养。
4.建构模型,渗透素养
师:说出图4中x、y的实际意义。
生9:如果x表示时间,y表示与出发地的距离,则可以理解为:小明以250m/min的速度匀速骑自行车,8min后到达某地,休息6min后,以200m/min的速度匀速返回,10min后返回出发地。
师:如果以上述行程问题为例,你还能提出哪些问题?
生10:如果2min后爸爸以100m/min的速度步行出发去追小明,几分钟后能追上他?
【设计意图】笔者给出函数图像,让学生自行赋予函数以实际意义,以“行程问题”让学生尝试提出、解决问题,体验函数建模的完整过程,有助于学生形成良好的思维能力,有利于培养学生的数学核心素养。
5. 明晰路径,构建体系
编题1:已知一次函数y=-4x+20,至少提出一个与此函数相关的问题。
编题2:一辆汽车从甲地出发驶向乙地,汽车以60km/h的速度行驶了xh,试根据上述情境提出问题,并用一次函数相关知识求解。
【设计意图】学生在编题过程中需要把各种相关知识重新组织、整理,能有效巩固和拓展所学知识,提升对所学知识的理解和认识,同时还能拓展思考问题的维度,强化知识间的内在联系,从而完成一次函数知识体系的构建。
三、教学反思
数学单元整体设计注重层次性、探究性、开放性和应用性等特性,笔者通过单元整体设计教学,在原有教学方法的基础上进行优化和创新,把握学生现有认知水平以及可能出现的思维障碍,唤醒学生的问题意识,以问题渗透的方式,启发深度思维,开展深度学习,促进了学生抽象思维和整体思维的形成,有助于学生对知识的整体把握,以及知识水平的提高。
(作者单位:江苏省太仓市第一中学)

