不动点集为Dold流形P(2,15)的对合

赵素倩,张卓琳,魏祥林

(河北科技大学理学院,河北石家庄 050018)

1 预备知识及引理

本文中,系数群是模2整数加群Z2,2N中的N是充分大的正整数,ω表示全Stiefel-Whitney类,ωi表示第i个Stiefel-Whitney类,σi(x)表示第i个基本对称函数∑x1x2…xi,[M]表示流形M的基本同调类。

设(Mr,T)是一个带有光滑对合T的r维光滑闭流形,T在Mr上的不动点集为F=∪Fr-k,其中Fr-k是不动点集F的(r-k)维分支的并;设λk是Fr-k在Mr中的法丛。由文献[20]可知,带有对合的流形(Mr,T)的协边类由其不动点集(Fr-k,λk)的法丛的协边类决定。

引理1(Kosniowski-Stong定理)[21]设f(x1,x2,…,xr)是Z2上的任意对称多项式,它的次数deg(f(x))≤r,则有示性数公式

(1)

其中表达式中的对称多项式可用基本对称多项式σi(x),σi(y),σi(z)表示,分别用Mr,λk,Fr-k的第i个Stiefel-Whitney类ωi(Mr),ωi(λk),ωi(Fr-k)代替σi(x),σi(y),σi(z)后,式(1)两边得到的是上同调类分别在基本同调类上作用的值。

引理2[21]设σi(x1,…,xk,xk+1,…,xr)是r个变元的第i个基本对称多项式,则

引理3[21]设{(Fr-k,λk)}(0≤k≤r)是流形上的一组向量丛,则其为某个对合(Mr,T)的不动点数据的充要条件是对于所有次数小于r的对称多项式f,都有

令P(m,n)表示Dold流形,则它的模2上同调环为

H*(P(m,n);Z2)=Z2[a,b]/(am+1=bn+1=0),

其中a∈H1(P(m,n);Z2),b∈H2(P(m,n);Z2)是生成元,它的全Stiefel-Whitney类是ω(P(m,n))=(1+a)m(1+a+b)n+1。

引理4[22]设P(m,n)是一个(m+2n)维Dold流形,则在P(m,n)上存在向量丛,其Stiefel-Whitney类为

1)1+a+b+a2,m=2,n≥1;

2)(1+a+b+a2)2,m=4,5,n≥2;

3)(1+a+b+a2)2(1+a+b)+a6,m=6,n≥1;

4)1+a2b3,m=2,n=3。

这样P(m,n)上的任意向量丛的全Stiefel-Whitney示性类都可表示为这些类与若干个类(1+a)和(1+a+b)之积。其中a∈H1(P(m,n);Z2)和b∈H2(P(m,n);Z2)是生成元。

若(M32+k,T)(k>0)是一个光滑闭流形,T是M32+k上的光滑对合,则对合的不动点集为F=P(2,15)。令λ→F是F在M32+k中的法丛。设a∈H1(P(2,15);Z2)和b∈H2(P(2,15);Z2)是生成元,P(2,15)的全Stiefel-Whitney类为ω(P(2,15))=(1+a)2(1+a+b)16。由引理4可知,λ的全Stiefel-Whitney示性类的形式为ω(λ)=(1+a)c(1+a+b)d,c,d为非负整数,或ω(λ)=(1+a+a2+b)(1+a)m(1+a+b)q,m,q为非负整数,则a2b15[P(2,15)]=1。

由于(1+a)4=0,(1+a+b)16=0,如果c≡c′(mod 4),则(1+a)c=(1+a)c′,故假设c<4,如果d≡d′(mod 16),则(1+a+b)d=(1+a+b)d′,故假设d<16。

2 主要结果

定理1设(M32+k,T)是带有光滑对合T的32+k(k>0)维光滑闭流形。T的不动点集为F=P(2,15),则(M32+k,T)存在且协边于零。

对ω(λ)=(1+a)c(1+a+b)d和ω(λ)=(1+a+a2+b)(1+a)m(1+a+b)q2种形式分别进行证明。

2.1 ω(λ)=(1+a)c(1+a+b)d的情况

根据c和d的奇偶性,分以下几种情况进行讨论。

命题1若d为奇数,对合(M32+k,T)不存在。

证明当d与c均是奇数时,假设对合(M32+k,T)存在,此时c+2d≥3,所以k≥3。

取

因为deg(f(x))=32<32+k,故f(x)[M]=0,但根据引理1,有

从而推出矛盾,所以对合(M32+k,T)不存在。

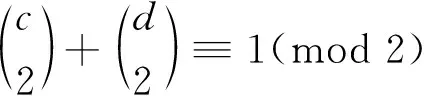
取

因为deg(f(x))=32<32+k,故f(x)[M]=0,但由引理1可知:

从而推出矛盾,因此对合(M32+k,T)不存在。

当d为奇数、c为偶数时,假设对合(M32+k,T)存在,此时c+2d≥2,所以k≥2。由引理2得

取

因为deg(f(x))=32<32+k,故f(x)[M]=0,但依据引理1有

从而推出矛盾,所以对合(M32+k,T)不存在。

综合以上讨论,命题1成立。下面讨论d为偶数的情况。

命题2若d为偶数,则对合(M32+k,T)存在且协边于零。

证明因为d是偶数,ω(P(2,15))=(1+a)2,ω(λ)=(1+a)c(1+a+b)d,所以在计算示性类时,所有项中都不会出现a2b15,于是对任何次数小于32+k的对称多项式f(x),都有

所以对合(M32+k,T)存在。又由于对合(M32+k,T)法丛的所有Stiefel-Whitney示性数全为零,因此,对合(M32+k,T)协边于零,故命题2得证。

综合命题1和命题2,当ω(λ)=(1+a)c(1+a+b)d时,对合(M32+k,T)存在且协边于零。

2.2 ω(λ)=(1+a+a2+b)(1+a)m(1+a+b)q的情况

根据m和q的奇偶性,分以下几种情况进行讨论。

命题3 若q为偶数,则对合(M32+k,T)不存在。

证明 若q为偶数、m为偶数,由引理2可得

取

其中deg(f(x))=32<32+k,故f(x)[M]=0。但根据引理1有

从而推出矛盾,所以对合(M16+k,T)不存在。

若q为偶数、m为奇数,由引理2得

取

其中deg(f(x))=32<32+k,故f(x)[M]=0,但根据引理1,有

从而推出矛盾,因此对合(M32+k,T)不存在。

综合以上讨论,命题3成立。下面讨论q为奇数的情况。

由于ω(λ)=(1+a+a2+b)(1+a)m(1+a+b)q=(1+a2b+b2)(1+a)m(1+a+b)q-1(q≥1),在下面的证明中,应用ω(λ)=(1+a2b+b2)(1+a)m(1+a+b)q-1。

命题4 若q为奇数,则对合(M32+k,T)存在且协边于零。

证明 分以下2种情形说明。

1)当q=1时,有

由于ω(P(2,15))=(1+a)2,所以穷尽所有情况,在计算示性类时,所有项中都不会出现a2b15,类似于命题2的证明,对合(M32+k,T)存在且协边于零。

2)当q=5时,有

ω(λ)=(1+a2b+b2)(1+a)m(1+a+b)4=(1+a)m(1+b4+a2b+a2b5+b2+b6)=

由于ω(P(2,15))=(1+a)2,所以穷尽所有情况,在计算示性类时,所有项中都不会出现a2b15,所以对合存在且协边于零。

3)当q=9时,有

由于ω(P(2,15))=(1+a)2,所以穷尽所有情况,在计算示性类时,所有项中都不会出现a2b15,所以对合存在且协边于零。

4)当q=13时,有

(1+b4+b8+b12+a2b+a2b5+a2b9+a2b13+b2+b6+b10+b14)=

由于ω(P(2,15))=(1+a)2,所以穷尽所有情况,在计算示性类时,所有项中都不会出现a2b15,所以对合存在且协边于零。

综上所述,在这种情况下,对合(M32+k,T)存在且协边于零。

1)当q=3时,若m是奇数,有

ω(λ)=(1+a2b+b2)(1+a)m(1+a+b)2=(1+a2b+b2)(1+a+b)2(1+a)m=

若m是偶数,有

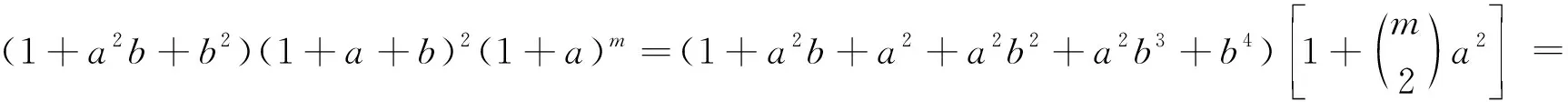
由于ω(P(2,15))=(1+a)2,所以穷尽所有情况,在计算示性类时,所有项中都不会出现a2b15,所以对合存在且协边于零。

2)当q=7时,若m是奇数,有

ω(λ)=(1+a2b+b2)(1+a)m(1+a+b)6=

若m是偶数,有

ω(λ)=(1+a2b+b2)(1+a)m(1+a+b)6=

由于ω(P(2,15))=(1+a)2,所以穷尽所有情况,在计算示性类时,所有项中都不会出现a2b15,所以对合存在且协边于零。

3)当q=11时,若m是奇数,有

ω(λ)=(1+a2b+b2)(1+a)m(1+a+b)10=

若m是偶数,有

ω(λ)=(1+a2b+b2)(1+a)m(1+a+b)10=

由于ω(P(2,15))=(1+a)2,所以穷尽所有情况,在计算示性类时,所有项中都不会出现a2b15,所以对合存在且协边于零。

4)当q=15时,若m是奇数,有

取

其中deg(f(x))=4<32+k,故f(x)[M]=0,但根据引理1,有

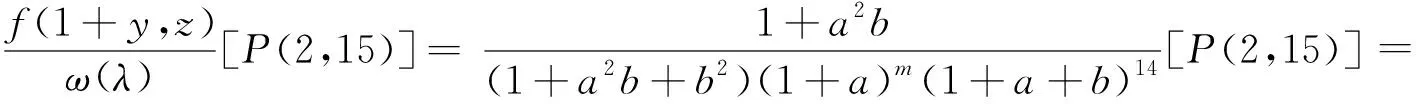
从而推出矛盾,对合不存在。

若m是偶数,有

取

其中deg(f(x))=4<32+k,故f(x)[M]=0,但根据引理1,有

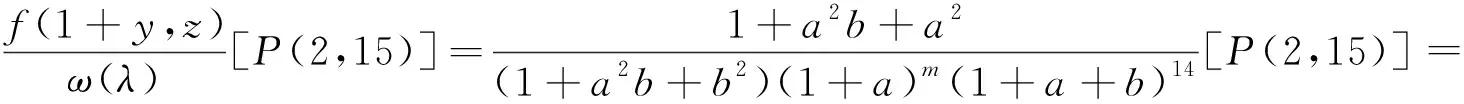
从而推出矛盾,对合不存在。

综上所述,在这种情况下,对合(M32+k,T)存在且协边于零,命题4得证。

综合命题1—命题4,定理1得证。

3 结 语

本文利用微分周期映射、示性类理论等,借助Kosniowski-Stong给出的M的示性数与不动点集法丛(F,λ)示性数之间的关系,通过构造合适的对称多项式出现矛盾,否定对合流形的存在性,或者证明对任意对称多项式都满足Kosniowski-Stong定理,说明对合的存在性,证明了不动点集F为Dold流形P(2,15)时,带有对合T的光滑闭流形(M,T)存在且协边于零。研究结果丰富了不动点集是Dold流形的对合的等变协边分类问题,也为研究不动点集其他特殊流形的对合提供了借鉴和参考。

本文研究的仅是不动点集F为特殊维数的Dold流形对合的协边分类,对于不动点集为F=P(2,2n+1)的情形还需要做进一步研究。