水下爆破振动及冲击波传播规律数值模拟分析*
石晨晨 程贵海 陈宏涛 李郎 周泰安 周勇
(1.中铁二局集团成都新技术爆破工程有限公司,四川成都 610000;2.中国中铁爆破安全技术研发中心,四川成都 610000;3.广西大学,广西南宁 530004)
0 引言
在国家战略“积极调整运输机构,发展绿色交通体系”的历史机遇下,国家对于航运事业的发展日趋重视,开始着重建设发展水运工程,因而水下爆破的应用在港口码头建设、航道疏浚等工程中越来越广泛。目前,水下钻孔爆破是水下工程爆破运用最多的方法。由于水下爆破存在地质条件复杂、水深条件变化较大、爆破效果受水深影响大、传统机械施工限制等原因,使得复杂条件下水运工程的建设成本较高、施工进度较慢,加之水下爆破技术难度高、爆破有害效应监测困难,造成了不同水深条件下爆破有害效应的传播衰减规律相关研究成果较少,无法充分采用现有成果对相关爆破设计参数的安全性进行提前性预测及检验。为了研究不同水深对爆破有害效应传播衰减的影响,相关学者开展了一系列的数值模拟及现场试验研究工作。唐晒华等[1]采用ANSYS建立了不同水深条件下的边坡稳定性数值模拟计算模型,获得了不同水深影响下边坡安全系数的变化规律。李春军等[2]结合实际工程采用LS-DYNA建立了水下基坑及基槽开挖工程的数值模拟模型,得到不同水深条件下爆炸冲击波拉应力峰值,通过非线性拟合方法得到了不同水深条件下不同炮孔距离的峰值拉应力理论值计算表,但未提出具体数学模型。司剑峰[3]采用水下冲击波传感器通过实测方法对厦门港古雷航道二期扩建工程的爆破冲击波进行了测试,通过线性回归分析,得出了相应的计算公式,据此给出了不同水深条件下对于人、木船、铁船的安全距离。
目前,水下爆破振动及冲击波预测相关研究成果仍较少,无法为既有的爆破设计参数是否合理提供判据及预测,亟需开展相应研究以提前检验相关水下爆破设计参数是否合理和对应参数所产生的爆破振动及冲击波危害是否处于国家标准规范要求值以内,以确保水下爆破安全。因此,研究水深的变化对水下钻孔爆破振动速度及冲击波强度的传播衰减规律,对于工程选取合理的钻爆参数、起爆方法及有害效应控制措施具有重大意义。
1 水下爆破孔网参数设计
1.1 工程概况
西江贵港至梧州航道水下爆破工程所属区域共包括3 个部分。其中,长洲坝段位于梧州市区域内,贵港至桂平航道段全线沿郁江下段弯曲展布,多数处于郁江流域平原区内,部分为低山丘陵区,覆盖层以砂卵砾石为主,局部为基岩裸露,岩体主要为砂岩及灰岩。爆区范围内渔业资源丰富,且临近城镇建筑物,两岸设有防洪堤,北岸一侧是009 乡道,沿乡道有大片居民房,南岸一侧是沿江路,也有大片居民房。爆区水深5 ~20 m,距离爆区50 m 为联通南北岸一桥墩,钻爆船只停泊距离为100 m,爆区距离保护建筑最近距离为165 m。
1.2 爆破设计参数
1.2.1 钻孔深度L
开挖高度H 取3 m,则垂直钻孔深度L 为:
式中,C 超深取1.0 ~2.0 m,为避免欠挖取大值。
1.2.2 抵抗线W
抵抗线W 根据下式确定:
式中,K为与岩性相关的系数,取值30,经计算,W取为2.7 m。
1.2.3 炮孔孔距a、炮孔排距b
为了提高炸药利用率,设计采用宽孔距、小排距布孔方案,采用梅花形方式进行布孔,炮孔孔距a 和炮孔排距b 依照以下规则选取:
式中,f 为孔间距与抵抗线间的关系系数,岩性较好时取f为1.0 ~1.25,岩性较差时,取f为1.25 ~1.5,本工程取f=1.1;m 为炮孔布置的密集系数,本工程取m 值为0.5。
1.2.4 单孔装药量
水下爆破施工时,单孔装药量的确定如下:
其中K 为水深影响系数,q 为炸药单位消耗量,其余参数含义同上。
1.2.5 爆破网路设置
本工程设计采用逐孔起爆网路,各孔间设置了50 ms 的延时时间,最大单孔药量即最大段药量为21 kg[4]。
2 不同水深条件下水下爆破模型
由于该工程设计为逐孔起爆技术,为了减小不同模型建模时间及运算成本,建立了不同水深条件下的多孔爆破数值模拟模型,水深变化通过关键字进行修改,不单独建模。
水下爆破模型由岩石层、水介质层、空气层组成,如图1 所示。当进行特定水深研究时,其上部通过关键字定义将其赋予空气属性,炸药通过坐标进行定义part 及材料属性。岩层厚度为8 m,根据实际工程爆破设计参数建立数值分析模型。需要模拟的工况为:水深为5 、8 、12 、15 m 的水下多孔爆破模型。

图1 水下爆破有限元模型
2.1 材料本构模型及状态方程
LS-DYNA 的材料特性需要本构模型和状态方程来描述。本构模型一共有4 种材料,分别为岩体、水、炸药及空气,4 种材料的本构模型和状态方程如下所述。
1)岩体材料。岩体的本构模型采用*MAT_PLASTIC_KINEMATIC 相应材料。
长洲枢纽位于龙圩水道上游,根据岩芯钻采取样数据,可以得到模拟岩石计算参数。具体岩石材料模型参数如表1 所示[5]。

表1 岩石材料及计算参数
2)爆炸介质及状态方程。炸药采用材料模型*MAT_HIGH_EXPLOSIVE_BURN,结合JWL 状态方程描述炸药产生的爆轰压力,具体如式(1)所示:
式中,参数A、B、R1、R2、为JWL 特征参数;E 为炸药蕴含内能;V 为相对体积;表2 为炸药材料参数。

表2 乳化炸药材料参数
3)水和空气采用*MAT_NULL 描述,用*EOS_GRUNEISEN表征其状态方程,其密度分别为1 000、1.225 kg/m3[6-7]。
3 不同水深条件下水下爆破数值模拟
分别分析了水深为5、8、12、15 m 不同工况下的水下爆破工程,由于篇幅有限,仅以典型的8 m 水深工况进行分析。
炸药起爆后,随即产生的爆轰波从起爆位置开始往顶部和四周扩散,具体过程如图2 所示。
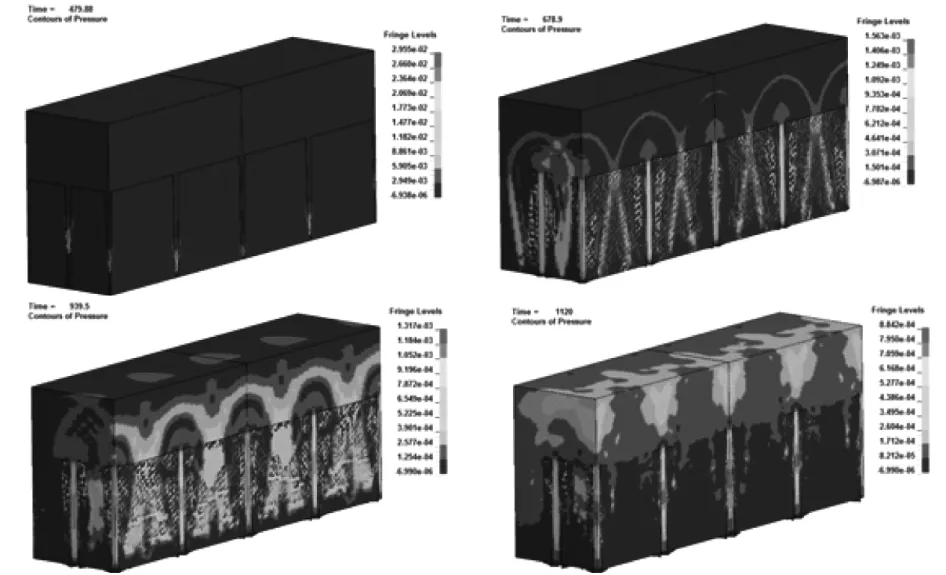
图2 不同时刻炸药爆轰状态
由图2 可知,t=479.88 ms 时,各炮孔炸药被雷管逐一引爆;t=678.90 ms 时,炮孔内炸药呈现明显的爆轰压力传递至水介质与岩体的接触分界面;t=939.50 ms 时,爆轰波传递到相邻炮孔附近且发生强烈干涉叠加现象,炸药爆轰能量从水堵塞的炮孔中开始向水域释放,炮孔周围岩石介质压力基本达到峰值,岩石部分被压碎破坏,由于岩石的夹制作用,压应力作用时间较短加之岩体抗压强度远远大于抗拉强度,距离炮孔较远的区域未被压碎,但切向拉应力会将炮孔拉裂;随后在t=1 120.00 ms 时,能量传递到空气与水介质交界面时发生反射,与原先产生的能量波发生叠加,可以明显地观察到交界处发生压力徒增且达到峰值现象,且反射产生较大的拉应力,引起上层岩体抗拉强度小于所达到岩体界面的拉应力,引起片落,部分岩体被拉应力破坏,随后炮孔周围岩体在水楔作用及水下冲击波的反复脉动条件下,岩体被破碎分裂。
4 不同水深条件下爆破振动分析
分别提取了不同水深条件下距爆源5、7、10、12、15、17、20 m 的7 个节点作为爆破振动的监测点,测点水平位置的布置不受水深变化影响,测点的坐标以爆源距测点水平距离L 进行表征,监测点布置于水面以下50 cm 处。
通过对数值模拟结果的分析,依据各单元监测节点处振速时程曲线中的峰值振速值,提取出了在各监测点位置的爆破振动峰值速度值,经统计如表3所示。所提取出的水深/距离与爆破振动峰值速度的关系曲线图如图3 所示。

表3 监测点爆破振动峰值速度

图3 水深/距离与爆破振动峰值速度的关系曲线
对关系曲线及表格数据进行分析可知,水平距离L 一致的情况下,水深H 对爆破振动峰值速度的影响较小,爆破振动峰值速度与水平距离L 可以数学模型进行表征。
根据图3 可以看出,L=20 m 时的数据出现了跳跃,故回归分析时进行了剔除。采用1stOpt 软件根据萨氏公式对爆破振动峰值速度与爆源距L间的关系进行回归分析,得出了可以表征爆破振动传播衰减规律的数学模型式(2):
式中,L 为距爆源水平距离。
为了验证拟合出的爆破振动表征公式的准确性,分别在距离爆区中心50 m 桥墩处、100 m 船舶停靠位置及165 m 建筑物地基上安装了爆破振动监测仪器。由于水深对爆破振动影响较小,故仅选取了8 m典型水深条件下的爆破振动测试结果与式(2)计算值进行了对比分析,表4 为预测值及实测值。
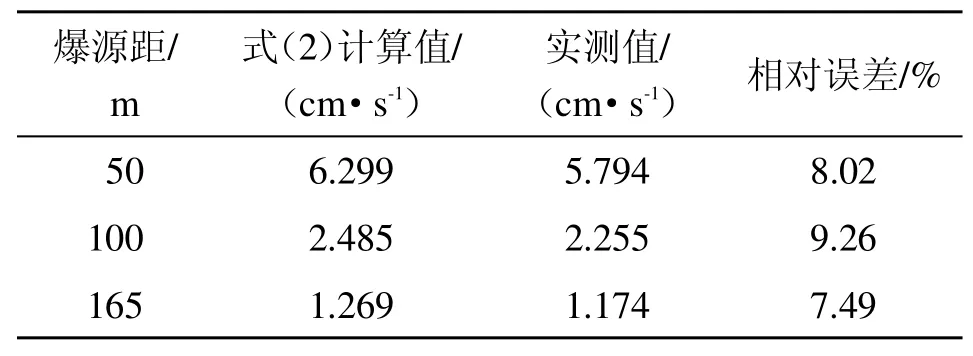
表4 爆破振动峰值速度实测值与式(2)计算值
经分析,式(2)预测精度高,平均相对误差仅为8.25%,预测精度达91.75%。
5 不同水深条件下爆破冲击波分析
冲击波分析方法与上述爆破振动研究方法相似,分别提取了不同水深条件下距爆源4、8、10、12、16、20 m 的6 个节点作为爆破冲击波的监测点,各测点所对应的水深也有相应变化,测点的坐标由水深H及距爆源距水平距离L 等2 个变量进行表征,监测点布置于水面以下50 cm 处。如图4 所示为所提取出的8 m 水深的爆破冲击波传播过程。
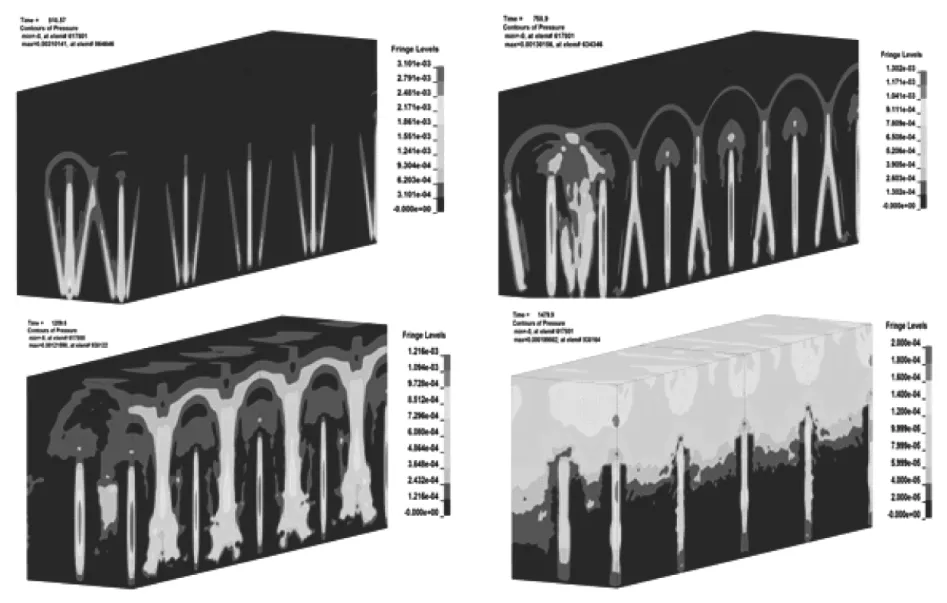
图4 8 m 水深条件下不同时刻水下爆破冲击波压力云图
由图4 可知,t=518.57 ms 时,首先起爆的炮孔产生的爆炸冲击波率先达到水下岩体近水层交界面,由于水介质的不可压缩性,水中局部密度增大,各炮孔间存在微差时间间隔,水下爆炸冲击波依次向外以球面波的形式进行传播,未经干涉直达介质表面的波可称之为直达波;t=758.9 ms 时,不同排的炮孔间所产生的冲击波发生强烈的干涉现象,2 排不同炮孔对称面处的冲击波由于干涉叠加效应,大大增加了水下爆炸冲击波的峰值压力及传播速度,同排炮孔间的冲击波由于微差间隔产生干涉相消,大大削弱了冲击波的峰值压力及传播速度;t=1 259.6 ms 时,水下爆破所产生的冲击波阵面到达水介质与空气的交界面,爆轰气体所形成的水球迅速向外扩展、破裂而产生脉动现象;t=1 479.9 ms 时,水下爆破冲击波到达水气界面后,反射产生拉伸波,并伴随着脉动现象至爆炸所释放的能量消耗殆尽。通过分析数值模拟过程可以得出水下爆破冲击波传播过程中会受到直达波压力、干涉叠加波压力以及脉动压力的综合作用,减弱任意一环节的影响则可以减弱冲击波的能量。
通过对数值模拟结果的分析,依据各单元监测节点处冲击波压力时程曲线中的监测结果,提取出了在各点位置的冲击波超压值,经统计如表5 及图5所示。

表5 监测点爆破冲击波压力值

图5 水深/距离与爆破冲击波的关系曲线
根据图5 可以看出,水下爆破冲击波与水深及距爆源水平距离均存在相关性。采用1stOpt 软件提供的拟合公式自动搜索功能对爆破冲击波峰值压力与水深H 及y 关系进行非线性回归分析,得出了可以表征爆破冲击波传播衰减规律的式(3):
6 试验验证
为了验证拟合出的水下爆破冲击波表征公式的准确性,分别在5、8、12、15 m 水深条件下,对距离爆区中心50 m 桥墩处、100 m 船舶停靠位置及165 m建筑物下部的水域安装了水下冲击波监测传感器,水下爆破冲击波实际检测值与式(3)计算值的对比见表6。

表6 检测点爆破冲击波压力值与计算值对比
根据表6 并经验算,式(3)拟合公式的平均相对误差为12.06%,预测精度为87.94%,该公式预测精度良好,能较为准确地反映该工程的水下爆炸冲击波传播衰减规律,可为实际工程提供参考。
7 结论
1)水下爆破振动振速峰值监测数据中,爆破振动速度随着爆心距L 的增加,不同水深条件下的各监测单元节点和振速都不断衰减,直至爆心距17 m趋于最小,但由于水体与空气接触面应力波的反射影响,导致20 m 测点所测振速要比17 m 测点大。
2)水下爆破冲击波峰值压力监测数据中,距离炮孔最近的测点监测到的压力峰值最大,随着水平距离的拉远,后续监测到的压力峰值呈指数衰减,水中冲击波压力峰值在水平距离不断增加的情况下衰减速度增快,为了预防水下冲击波的危害,可合理设置警戒距离,以减小冲击波对保护对象的损害。
3)水深对水下爆破冲击波的影响较大,随着水深的增加,相同测点的冲击波压力峰值有所下降,这是由于水下爆破冲击波受到直达波压力、干涉叠加波压力以及脉动压力的综合作用,实际工程中可利用此原理,采用气泡帷幕发生器或其他小药量裸露药包进行干涉相消,进一步削弱爆破冲击波的传播。本工程中综合采用了气泡帷幕缓冲法及逐孔起爆干涉法,对各炮孔间所产生的冲击波进行削峰,冲击波控制效果良好,水下爆破过程未造成大面积渔类死亡,各保护对象均无损伤。
4)通过实际工程验证,采用软件自动搜索拟合功能,得出了反映该工程水下爆破振动峰值速度的非线性数学模型为其预测精度达91.75%,预测精度高。
5)通过实际工程验证,采用软件自动搜索拟合功能,得出了反映该工程水下爆破冲击波压力的非线性数学模型为Pm=0.367+18.665×H-0.885× y0.968,其预测精度精度达87.94%,预测精度良好。
6)通过对数值模拟得出相关数据,结合数值模拟结果拟合出的爆破振动及冲击波的预测公式,可以为实际水下爆破工程中的有害效应预测提供方法及手段,也可作为水下爆破有害效应控制的相关依据,同类工程可供参考。在实际工程中,可将试爆试验数据结合数值模拟分析结果,以进一步选取更为适合的水下爆破参数,减少爆破有害效应,确保施工安全。

