暴雨致灾机理分析及预测模型构建*

王卓颖 南华

（河南理工大学能源科学与工程学院，河南焦作 454000）

0 引言

随着全球气候环境的不断变化，极端降雨情况出现的频率逐年递增，山地、公路边坡等区域易发生山体滑坡、泥石流等地质灾害，具有影响范围广、破坏性强等特点，严重影响了区域生态环境和交通道路安全［1-3］。生态护坡技术是近些年边坡防护技术中的主流方法，通过植物茎叶的水文效应与根系的锚固作用，实现对土体的防护和加固，以减小自然灾害的发生概率［4］。乔木具有根系发达、固土效果较好、生命力顽强等优点，是常见护坡植物之一［5］，而雨水入渗使土体发生非饱和-饱和渗流为引发乔木失稳的主要原因之一，极易诱发山体滑坡、泥石流等灾害［6-7］。因此，对乔木稳定性的预测可有效预防地质灾害的发生，以保护城市基础设施及交通道路的安全运营。

降雨对土体稳定性的影响机理十分复杂，土壤性质、降雨强度、瞬态水压力、饱和水强度、孔隙水单位重量等因素均会影响土体的稳定性［8-9］，而植物根系利用其锚固及黏结作用可与土壤形成一个更为复杂的结构体［10］，故降雨对根-土复合结构的影响属于多因素影响的非线性回归问题。线性回归、经验方程及神经网络是目前常见的预测方法，其中，反馈式（Back Propagation）神经网络是近些年最成熟的神经网络模型之一，非常适合解决非线性回归问题［11-12］。BP神经网络目前已应用于高边坡土壤水分预测、结构施工安全智能预测等方面，均取得了较好的效果［13-16］。但是BP 神经网络预测模型需要大量的样本数据进行训练［17］，而降雨对乔木稳定性影响情况的相关数据较少，故限制了神经网络技术在暴雨致灾预测系统中的应用。

本文将理论分析、数值模拟与神经网络相结合，以乔木根系固土机理和非饱和土体力学特征为基础，分析失稳原因并构建几何模型，利用数值模拟为BP神经网络预测模型提供训练样本，同时预测模型也解决了数值模拟计算时间长的问题。结果表明，本文所构建的暴雨致灾预测模型不仅预测精度高，而且计算速度相比于数值模拟提高了数万倍，可及时预判坡体的稳定性，为救灾措施（搬迁、疏散等）的制定及实施提供时间，以减小灾害所带来的损失。

1 暴雨致灾理论分析

1.1 乔木根系固土机理

土体的强度主要由土颗粒间的相互作用力决定，一般物体埋入土中，其主要受力只有与土颗粒之间的摩擦力。和木桩、电线杆等无根系物体不同，乔木根系发达，可与土体形成一个复杂的力学体系。乔木根系多被看做柔性材料，具有较高的抗拉强度，能抗剪，但抗弯性能较差，故根系附近的土体可以看做是加筋土，即乔木根系能大大提高土体的抗剪强度。

乔木的根系主要由须根和主根两部分组成，主根一般可达2 ～12 m，自表土层开始向下部各方向延伸，部分主根可穿过土体表层的松散风化层，锚固到深处稳定的岩土层上。主根周围大量的根毛和须根相互缠绕黏结，对土颗粒有粘结作用，可以使土颗粒紧密附着在主根周围。乔木根系的固土机理与全长树脂锚杆的锚固机理十分相似，如图1 所示。若将主根看作锚杆，那根毛和须根便可看作是树脂锚固剂，起到黏结锚杆杆体（主根）与孔壁岩石（土颗粒）的作用［18-19］。因此，后续的数值模拟中选用锚杆来模拟乔木根系。

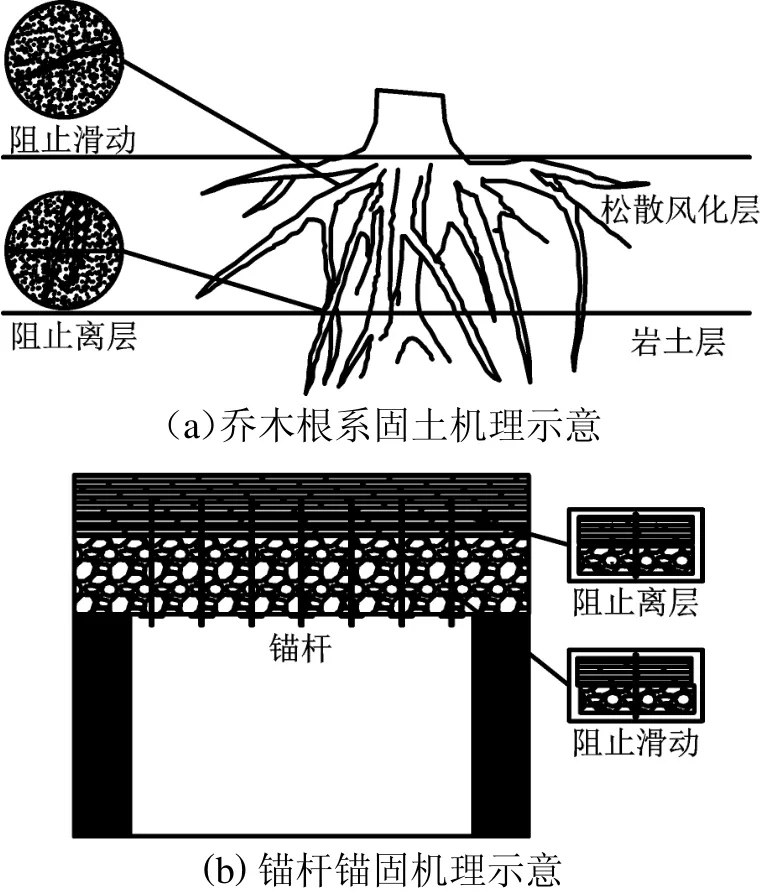
图1 乔木根系与锚杆作用机理对比

一般认为，非饱和土的渗透系数kw与孔隙比e和含水量（饱和度S）有关，并且含水量（饱和度S）对渗透系数的影响十分明显，故研究土体非饱和渗流的关键是建立非饱和渗透系数kw与含水量（饱和度S）之间的函数关系。在预测非饱和土渗透系数的模型中，认可度最高的是Van Genuchten（VG）提出的模型，该模型结合了土-水特征曲线（SWCC）与渗透系数模型，其模型方程为：式中，S 为饱和度；Sr为残余饱和度；Se为有效饱和度；为体积含水量；r为残余体积含水量；s为饱和体积含水量；a、m、n 分别为VG 模型拟合参数；s 为基质吸力。

根据式（1）可以得到体积含水量与基质吸力的关系为：

1.2 试验土体的物理力学性质

非饱和土的抗剪强度主要由真黏聚力、净法向应力所产生的摩擦力，以及吸力所产生的吸附强度或附加摩擦力3 部分组成，基质吸力（ua-uw）和净法向应力（ -ua）是2 个表示应力状态的独立变量。一般认为，土体吸附强度和含水量之间呈线性相关，非饱和土抗剪强度公式为［20］：

式中，f为土体破坏时破坏面上的剪应力；c'、'为有效强度参数，通过饱和土试验确定；为法向应力；ua为孔隙气压力；uw为孔隙水压力；s为饱和含水量。

在试验场地（河南省洛阳市嵩县山金矿区）按深度取土进行土壤含水率实验，其土质为粉质黏土，由实验测得土体参数见表1。所得数据结合式（2）拟合得到如图2 所示的SWCC 曲线。因为没有进气值和残余值2 个关键数据点的实验数据，所以图2 没有构成完整的SWCC 曲线。

表1 土体参数

图2 拟合SWCC 曲线

将试验所得数据代入SWCC 模型表达式（1）得到基本参数：a=0.06，m=0.48，n=1.71。饱和体积含水量s=0.493 8，r=0.08，则式（2）可变为：

2 降雨条件下乔木稳定性数值模拟

2.1 乔木根系简化模型

乔木具有粗壮高大的主干，护坡多选用小乔木，通常高度为5 ～10 m，根深可达2 ～12 m，后续选取高8 m、根深5 m、胸径0.6 m 的乔木进行模拟。乔木根系发达，往往相互缠绕、盘根错节，分布十分复杂，这使得数值模拟时难以准确模拟其形态，故本文旨在模拟其力学特征。以乔木根系固土机理为基础，结合其分布形态，将乔木根系简化为如图3 所示的模型。

图3 乔木根系简化模型（单位：m）

矿业工程中常采用FLAC3D模拟软件中的Cable 单元模拟锚杆。故本文先采用Rhino 软件建立如图3（b）所示的树根简化模型，后采用FLAC3D 中的Cable单元模拟乔木根系，通过赋参使锚杆不具有抗弯性能以模拟乔木根系的力学特征，同时调整Cable单元参数模拟全长注浆锚固以模拟根毛和须根的粘结作用，由实验测得根系参数见表2。

表2 乔木根系材料参数

2.2 建立几何模型

FLAC3D提供了二相流模型，适合模拟非饱和土［21］，故利用FLAC3D 建立几何模型如图4 所示。土体模型尺寸为15 m×15 m×30 m，采用Mohr-Coulom 本构模型，认为土体为各向同性渗流模型，顶面为自由边界条件同时设置渗流边界条件，其余各面均设置固定边界条件。乔木为不透水材料模型，与土体的接触界面设置为不透水边界。在得到稳定状态下的渗流场之后，添加降雨边界条件，在此基础上进行瞬态计算。

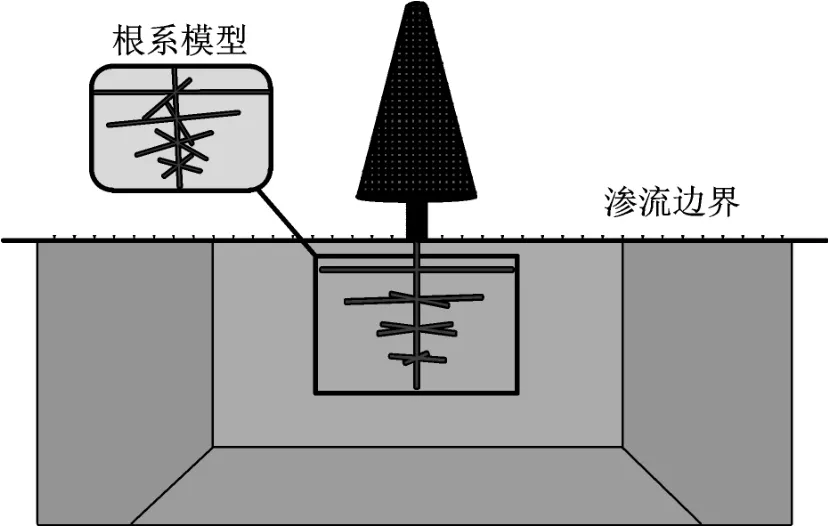
图4 数值模拟三维模型

2.3 降雨方案及渗流参数

为了使后续BP 神经网络训练出来的模型更符合实际情况，结合洛阳市近10 年的降雨情况，根据降雨强度的不同，制定了如下6 类契合实际的多雨型降雨方案，共计14 组不同降雨强度的模拟方案。拟利用数值模拟得到多种降雨条件下暴雨致灾样本，模拟时在乔木顶端施加一个稳定的上拔载荷，1—7h内每隔10 min 监测一次孔压及上拔位移的变化情况，故可得588 组不同降雨强度下的孔压及位移数据，相关的降雨参数见表3。

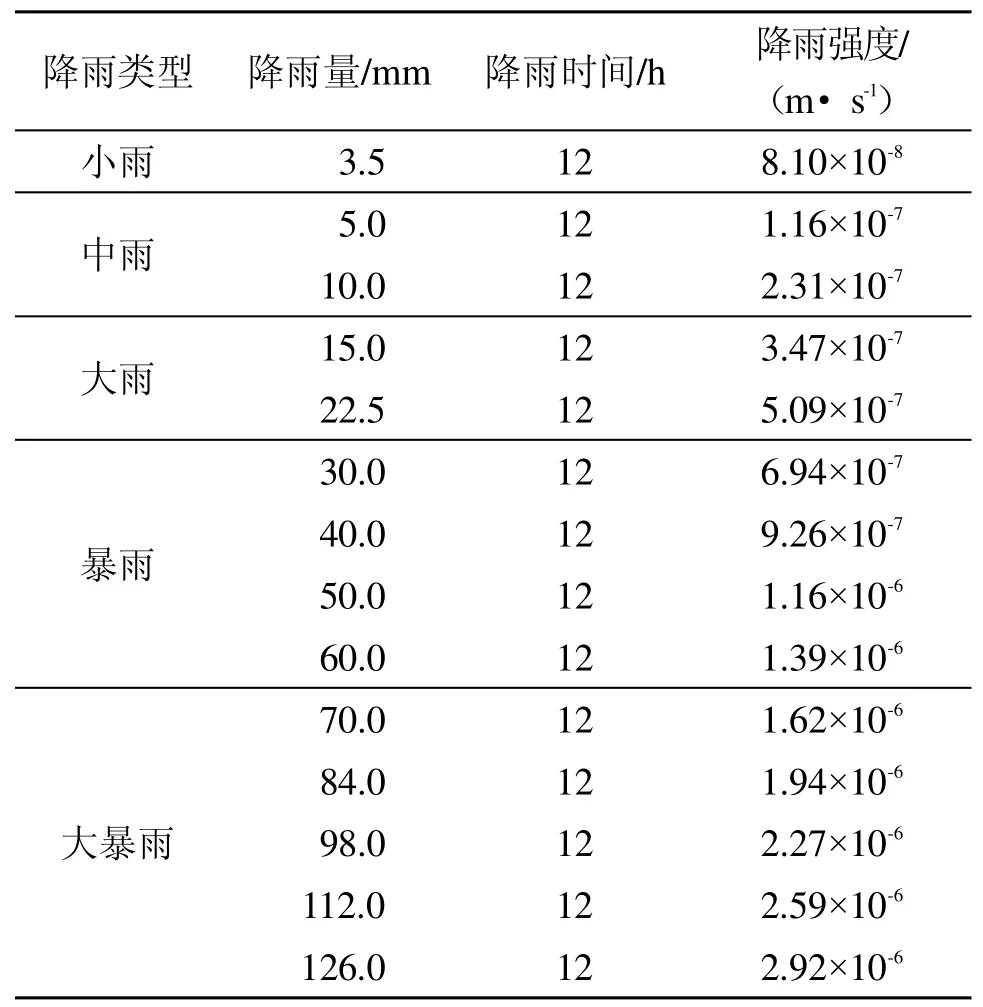
表3 各方案降雨参数

降雨入渗率是影响非饱和土体稳定性的重要因素［22］。根据非饱和土体的渗透特征可知，当降雨强度大于土体的渗透系数时，土体的入渗率即为土体渗透系数；当降雨强度小于土体的渗透系数时，土体的入渗率即为降雨强度。通过计算可知，当12 h 内的降雨量超过112.752 mm 时，降雨强度等于渗透系数，即此后土体的入渗率即为土体的渗透系数。数值模拟中非饱和土体的相关渗流参数见表4。

表4 非饱和土渗流参数

2.4 数值模拟结果分析

在距土体表面1 m 的位置设置监测点，对此处的孔隙水压力进行监测，可得到14 种降雨强度下的孔压及位移变化特征曲线，如图5 所示。根据非饱和土的强度特征可知，基质吸力等于孔隙气压力与孔隙水压力之差（ua-uw），由于土体与大气连通，故此处孔隙气压力默认为0，因此基质吸力即为负孔隙水压力。从图5（a）可以看出，土体经历了从非饱和到饱和的渗流过程，孔隙水压力由负值逐步增至正值，故基质吸力随着雨水入渗逐渐减小。同时，随着降雨强度的增大，孔压的变化梯度越大，即土体达到饱和所需时间越少。

图5 数值模拟监测曲线

降雨会使土体含水率增高，则乔木根系与土体之间的黏结及锚固效果将会减弱，故乔木的抗拔性能将逐步减弱。在乔木顶端给一稳定的上拔载荷（900 kPa），则可得到如图5（b）所示的不同降雨强度下的上拔位移变化特征曲线。由图5（b）可以看出，在降雨时间相同的情况下，随着降雨强度的增大，乔木上拔位移逐步增大。这是因为随着降雨强度的增大，土体含水率变化梯度也会增大，则基质吸力减小的速度随之增大，故上拔位移逐渐增大。

降雨引起的基质吸力变化是影响乔木稳定性的直接因素，降雨条件下基质吸力的衰减情况可由上木的渗埋比相同，则深径比越大，上拔位移变化系数越小，即基质吸力的衰减程度越不明显，树木的拔位移变化系数的函数关系式表述。定义无量纲自变量渗埋比和深径比：

式中，ht为乔木的根长；hd为雨水的入渗深度；Dt为乔木的根茎。

构建乔木上拔位移变化系数的函数关系式：

式中，Sn0为无降雨时乔木的上拔位移；Sn为雨水入渗深度为hd时乔木的上拔位移。

通过origin 拟合可得到双变量无量纲上拔位移变化系数拟合曲线如图6 所示。本文中上拔位移变化系数的具体表达式为：

图6 上拔位移变化系数拟合曲线

由式（8）可知，在某一确定的降雨条件下，若树安全稳定性越好，此表达式可为易受暴雨影响地区的道路设计及栽种树木选取提供参考。

3 基于BP 神经网络的预测模型

人工神经网络（ANNs）简称神经网络，是一种模仿动物神经网络行为特征，进行分布式并行信息处理的数学模型，主要通过调整内部大量节点之间相互连接的关系，从而达到处理信息的目的［22］。反馈式神经网络模型，即BP 神经网络模型，是一种按照误差逆向传播算法训练的多层前馈神经网络，是应用最广泛的神经网络模型之一，非常适合解决非线性回归问题［23］。

降雨对乔木稳定性的影响程度与降雨强度、降雨时间、乔木埋深、土体参数等多种因素相关，属于多因素影响的非线性回归问题。本文选用Matlab 软件建立基于BP神经网络的暴雨致灾预测系统，依靠数值模拟获得的588 组不同降雨方案下的暴雨致灾样本，其中任选14 组用作后续的模型验证，剩余样本中的70%（402 组）用作训练样本，15%（86 组）用作验证样本，15%（86 组）用作测试样本。

3.1 BP 神经网络预测模型

BP 神经网络的结构如图7 所示，主要包括输入层、隐含层以及输出层。本文的预测模型共有2×402个输入值，1×402 个输出值。由于训练样本有限，为防止神经网络出现过拟合现象，在降低模型复杂度的基础上，分别用Levenberg-Marquarbt、Bayesian Regularization、Scaled Conjugate Gradient 这3 个算法进行训练，降低单个模型的过拟合风险，最终选择训练效果最好的Levenberg-Marquarbt 算法。训练过程中，首先对输入值进行归一化处理，然后输入值向前传输，经过各隐含层之间的权值以及阈值b，最终至输出层输出结果，同时模型自动计算输出值与实际输出值之间的误差△e。若△e 没有达到设定的收敛值，则修改各层之间的、b，进入逆向反馈过程，直至达到预先设定的收敛值，即可停止训练。

图7 BP 神经网络结构

BP 神经网络预测模型可以根据相关系数R 的大小来判断模型的预测效果，R 越接近1，表示预测数据与模拟数据的拟合程度越高。BP 神经网络的训练过程曲线如图8 所示。可以看出，训练集、验证集、测试集以及整体训练模型的相关系数R 均大于0.99，未出现过拟合现象。由此可见，此暴雨致灾预测模型的拟合误差小、预测精度高。

图8 暴雨致灾预测模型训练过程曲线

3.2 预测模型准确性分析

为了进一步分析预测模型的准确性，选用无降雨时稳定载荷下乔木的最大上拔位移量进行基础拉拔实验对比分析，结果如图9 所示。由图9（a）可以看出，数值模拟结果与现场实测值之间的误差为1.34%，BP 神经网络预测模型与现场实测值之间的误差为2.29%，误差增加了0.95%，这是因为数值模拟与神经网络相结合时，2 种模型会产生误差叠加，但是误差仅为1.62%。相信随着神经网络算法的逐步完善和发展，其对训练样本的数量及质量要求也会逐渐降低，并且实测数据也在不断地丰富和完善中。未来将可以实现以实测数据作为训练样本，构建更客观精准的暴雨致灾预测模型。

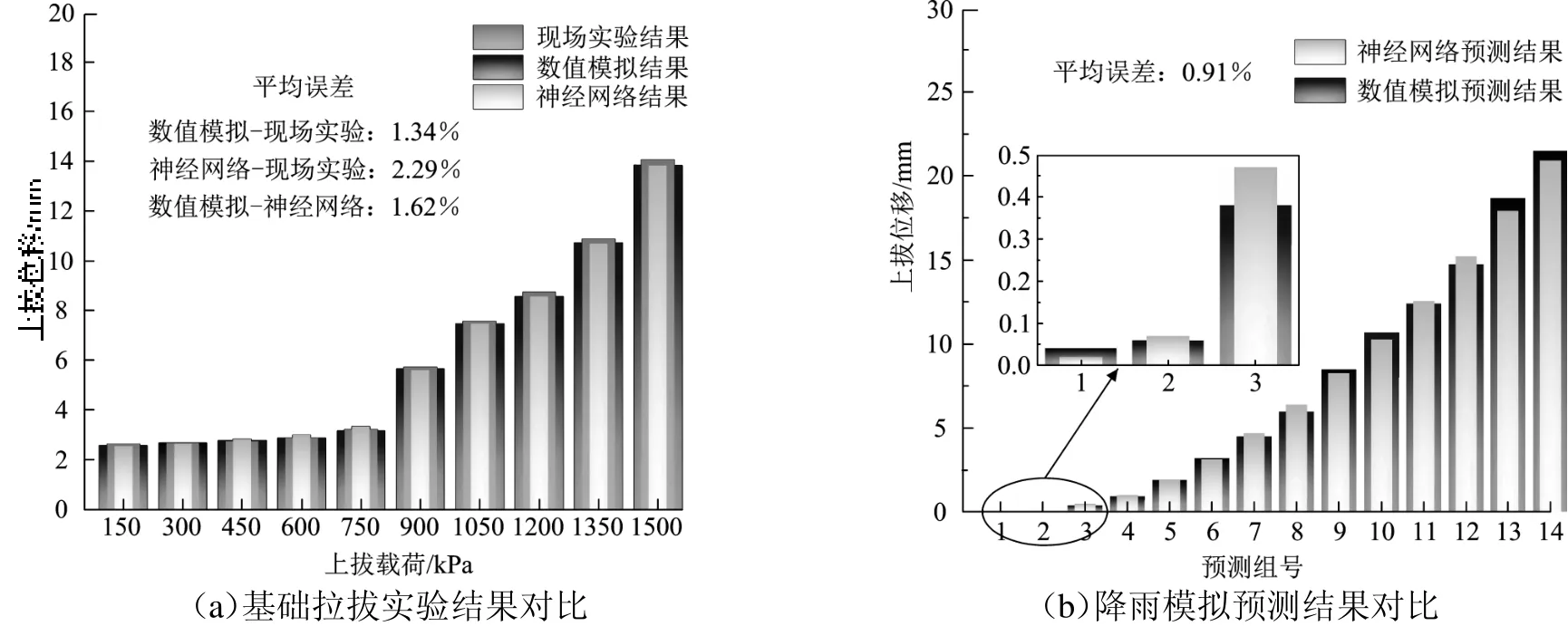
图9 模型准确性分析

利用未进行训练的14 组数据，在训练好的暴雨致灾预测模型中进行降雨模拟，记录随着降雨强度的改变树木在一稳定拉拔力下的位移变化情况，并与数值模拟数据进行对比分析。由图9（b）可以看出，数值模拟结果曲线与神经网络预测结果曲线吻合度较高，降雨模拟平均误差仅为0.91%。由图9 可以看出，BP神经网络预测模型和数值模拟结果接近，平均误差仅为1.265%，能反映不同降雨强度下乔木稳定性的变化情况。

此外，BP 神经网络预测模型计算一个7 h 的强降雨方案仅需0.1 s，而利用数值模拟软件则需耗费数小时，计算速度提高了数万倍。综上所述，本文所建立的基于BP 神经网络的暴雨致灾预测模型在节约计算时间的基础上，也满足了预测精度的要求，可在发生强降雨等突发暴雨灾害时及时做出反馈，以降低山体滑坡、泥石流等灾害所带来的损失，可为灾害预防工作提供参考。

3.3 分类预警评判指标

结合理论分析及预测结果制定分类预警评判指标及防治措施如表5 所示，可为台阶边坡及公路的灾害防治工作提供参考。

表5 分类预警评判指标

4 结论

1）基于非饱和土体力学特征和乔木根系固土机理，对数值模拟监测结果进行处理分析，得到双变量无量纲上拔位移变化系数的拟合曲线及其表达式，此表达式可为易受暴雨影响地区的道路设计及栽种树木选取提供参考。

2）将数值模拟与BP 神经网络相结合，提出新的暴雨致灾预测模型，此模型相比于数值模拟计算速度提高了数万倍，与数值模拟的误差也仅为1.265%，可为救灾措施的制定及实施提供更多时间。

3）根据理论分析及预测结果，制定与预测模型相对应的分类预警评判指标，共分为蓝、黄、红3 个等级，通过降雨对乔木稳定性的影响情况分析其护坡状况，并制定相应的防护措施，可为灾害防治工作提供参考。